2022-2023学年人教版八年级数学上册11.2.2三角形的外角同步练习(word版 含答案)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册11.2.2三角形的外角同步练习(word版 含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 318.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-05 14:20:24 | ||
图片预览



文档简介
11.2.2三角形的外角(同步练习)
班级: 姓名: 得分:
知识回顾
三角形的外角等于 。
三角形的外角和= 度。
同步训练
选择题。
1.下列叙述中正确的是( )
A.三角形的外角等于两个内角的和
B.三角形的外角大于内角
C.三角形的外角等于与它不相邻的两个内角和
D.三角形每一个内角都只有一个外角
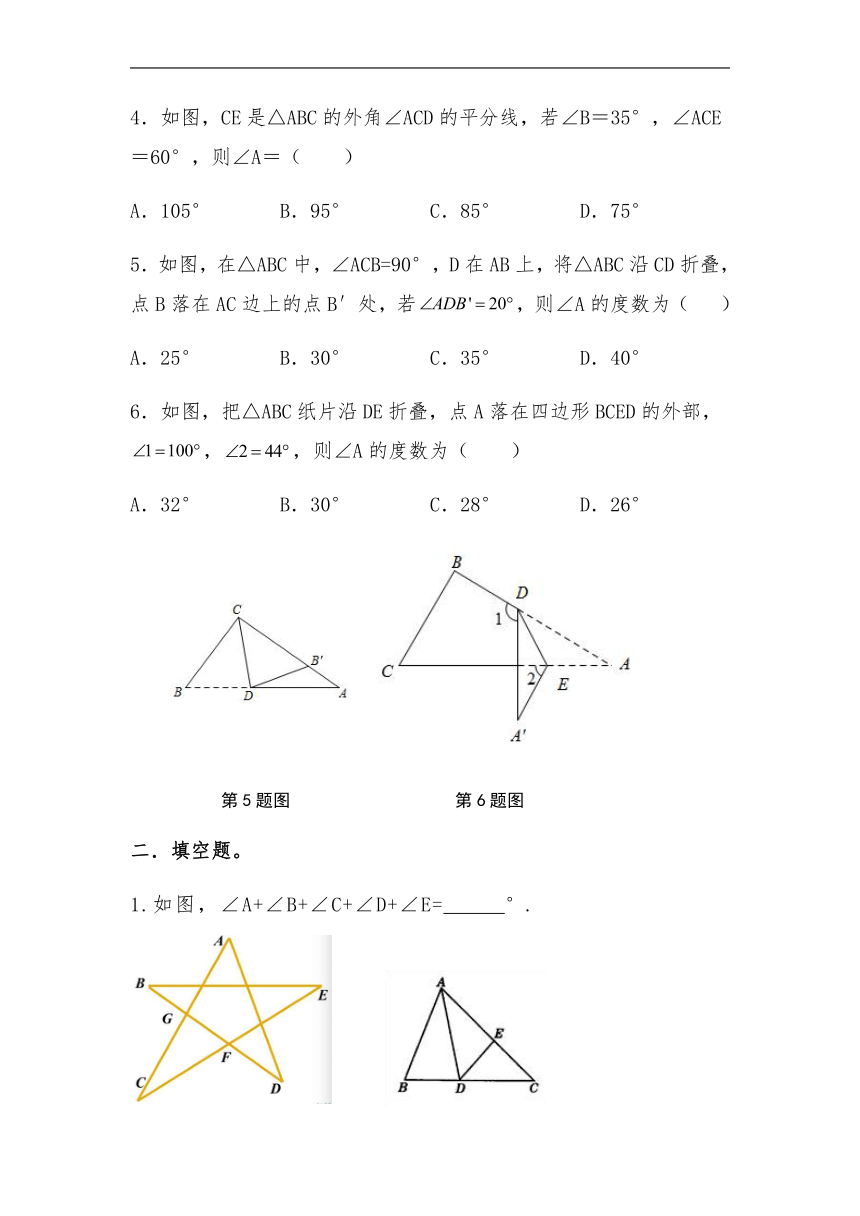
2.如图,在△ABC中,D是BC延长线上一点,∠B=40°,∠ACD=120°,则∠A等于( )
A.60° B.70° C.80° D.90°
第2题图 第3题图 第4题图
3.如图,∠BDC=98°,∠C=38°,∠B=23°,∠A的度数是( )
A.61° B.60° C.37° D.39°
4.如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=( )
A.105° B.95° C.85° D.75°
5.如图,在△ABC中,∠ACB=90°,D在AB上,将△ABC沿CD折叠,点B落在AC边上的点B′处,若,则∠A的度数为( )
A.25° B.30° C.35° D.40°
如图,把△ABC纸片沿DE折叠,点A落在四边形BCED的外部,,,则∠A的度数为( )
A.32° B.30° C.28° D.26°
第5题图 第6题图
填空题。
1.如图,∠A+∠B+∠C+∠D+∠E= °.
第1题图 第2题图
2.如图,在△ABC中,∠B=66°,∠C=54°,AD是∠BAC的平分线,DE平分∠ADC交AC于E,则∠ADE= .
3.已知,一个含角的直角三角板按如图所示放置,,则 .
第3题图 第4题图
如图,在△ABC中,BD平分∠ABC,连接CD,若∠A=∠D=40°,∠ACD=30°,则∠DCE的度数为 .
5.已知等腰三角形的一个外角为150°,则它的底角为 .
6. 如图,BP、CP是任意△ABC中∠B、∠C的角平分线,可知∠BPC=90°+∠A,把图中的△ABC变成图中的四边形ABCD,BP,CP仍然是∠B,∠C的平分线,猜想∠BPC与∠A、∠D的数量关系是 .
三.解答题。
1. 如图,∠A = 51°,∠B = 20°,∠C = 30°,求∠BDC 的度数.(用两种方法解答,有理即可)
2.如图,P 为△ABC 内一点,∠BPC=150°,∠ABP=20°,∠ACP=30°,求∠A 的度数.
3.下面是有关三角形内外角平分线的探究,阅读后按要求作答:探究1:如图(1),在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现:∠BOC=90°+∠A(不要求证明).
探究2:如图(2)中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的数量关系?请说明理由.
探究3:如图(3)中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的数量关系?(只写结论,不需证明).结论: .
4.△ABC中,AD是∠BAC的角平分线,AE是△ABC的高.
(1)如图1,若∠B=40°,∠C=60°,求∠DAE的度数;
(2)如图2,∠B<∠C,则DAE、∠B,∠C之间的数量关系为___________;
(3)如图3,延长AC到点F,∠CAE和∠BCF的角平分线交于点G,求∠G的度数.
参考答案
知识回顾:与它不相邻的两个内角的和,360
同步练习
选择题:CCCCCC
填空题:1.360;2.48°;3.75°;4.70°;5.30°或75°;6.∠BPC=(∠BAD+∠ADC)
解答题:
解法一:连接 AD 并延长到点 E.
在△ABD 中,∠1 +∠B =∠3,
在△ACD 中,∠2 +∠C =∠4.
∵∠BDC =∠3 +∠4,∠BAC =∠1 +∠2,
∴∠BDC =∠BAC +∠B +∠C= 51° + 20° + 30° = 101°.
解法二:延长 BD 交 AC 于点 E(或连接 CD 并延长交 AB 于 F)
在△ABE 中,∠1 =∠B +∠A,
在△ECD 中,∠BDC =∠1 +∠C.
∴∠BDC =∠A +∠B +∠C= 51° + 20° + 30° = 101°.
解法1 解法2
2.解:延长 BP 交 AC 于点 E,
则∠BPC,∠PEC 分别为△PCE,△ABE 的外角,
∴∠BPC=∠PEC+∠PCE,∠PEC=∠ABE+∠A.
∴∠PEC=∠BPC-∠PCE=150°-30°=120°.
∴∠A=∠PEC-∠ABE=120°-20°=100°.
3.解:(1)探究2结论:∠BOC=∠A,
理由如下:
∵BO和CO分别是∠ABC和∠ACD的角平分线,
∴∠1=∠ABC,∠2=∠ACD,
又∵∠ACD是△ABC的一外角,
∴∠ACD=∠A+∠ABC,
∴∠2=(∠A+∠ABC)=∠A+∠1,
∵∠2是△BOC的一外角,
∴∠BOC=∠2-∠1=∠A+∠1-∠1=∠A;
(2)探究3结论∠BOC=90°-∠A.
4.解:(1)∵∠B=40°,∠C=60°,∠BAC+∠B+∠C=180°,
∴∠BAC=80°,
∵AD平分∠BAC,
∴∠CAD=∠BAD=∠BAC=40°,
∵AE是△ABC的高,
∴∠AEC=90°,
∵∠C=60°,
∴∠CAE=90° 60°=30°,
∴∠DAE=∠CAD ∠CAE=10°;
(2)∵∠BAC+∠B+∠C=180°,
∴∠BAC=180° ∠B ∠C,
∵AD平分∠BAC,
∴∠CAD=∠BAD=∠BAC,
∵AE是△ABC的高,
∴∠AEC=90°,
∴∠CAE=90° ∠C,
∴∠DAE=∠CAD ∠CAE=∠BAC (90° ∠C)=(180° ∠B ∠C) 90°+∠C=∠C ∠B,
即∠DAE=(∠C ∠B).
故答案为:∠DAE=(∠C ∠B).
(3)设∠ACB=,
∵AE⊥BC,
∴∠EAC=90° ,∠BCF=180° ,
∵∠CAE和∠BCF的角平分线交于点G,
∴∠CAG=∠EAC=(90° )=45° ,
∠FCG=∠BCF=(180° )=90° ,
∵∠FCG=∠G+∠CAG,
∴∠G=∠FCG ∠CAG=90° (45° )=45°.
班级: 姓名: 得分:
知识回顾
三角形的外角等于 。
三角形的外角和= 度。
同步训练
选择题。
1.下列叙述中正确的是( )
A.三角形的外角等于两个内角的和
B.三角形的外角大于内角
C.三角形的外角等于与它不相邻的两个内角和
D.三角形每一个内角都只有一个外角
2.如图,在△ABC中,D是BC延长线上一点,∠B=40°,∠ACD=120°,则∠A等于( )
A.60° B.70° C.80° D.90°
第2题图 第3题图 第4题图
3.如图,∠BDC=98°,∠C=38°,∠B=23°,∠A的度数是( )
A.61° B.60° C.37° D.39°
4.如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=( )
A.105° B.95° C.85° D.75°
5.如图,在△ABC中,∠ACB=90°,D在AB上,将△ABC沿CD折叠,点B落在AC边上的点B′处,若,则∠A的度数为( )
A.25° B.30° C.35° D.40°
如图,把△ABC纸片沿DE折叠,点A落在四边形BCED的外部,,,则∠A的度数为( )
A.32° B.30° C.28° D.26°
第5题图 第6题图
填空题。
1.如图,∠A+∠B+∠C+∠D+∠E= °.
第1题图 第2题图
2.如图,在△ABC中,∠B=66°,∠C=54°,AD是∠BAC的平分线,DE平分∠ADC交AC于E,则∠ADE= .
3.已知,一个含角的直角三角板按如图所示放置,,则 .
第3题图 第4题图
如图,在△ABC中,BD平分∠ABC,连接CD,若∠A=∠D=40°,∠ACD=30°,则∠DCE的度数为 .
5.已知等腰三角形的一个外角为150°,则它的底角为 .
6. 如图,BP、CP是任意△ABC中∠B、∠C的角平分线,可知∠BPC=90°+∠A,把图中的△ABC变成图中的四边形ABCD,BP,CP仍然是∠B,∠C的平分线,猜想∠BPC与∠A、∠D的数量关系是 .
三.解答题。
1. 如图,∠A = 51°,∠B = 20°,∠C = 30°,求∠BDC 的度数.(用两种方法解答,有理即可)
2.如图,P 为△ABC 内一点,∠BPC=150°,∠ABP=20°,∠ACP=30°,求∠A 的度数.
3.下面是有关三角形内外角平分线的探究,阅读后按要求作答:探究1:如图(1),在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现:∠BOC=90°+∠A(不要求证明).
探究2:如图(2)中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的数量关系?请说明理由.
探究3:如图(3)中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的数量关系?(只写结论,不需证明).结论: .
4.△ABC中,AD是∠BAC的角平分线,AE是△ABC的高.
(1)如图1,若∠B=40°,∠C=60°,求∠DAE的度数;
(2)如图2,∠B<∠C,则DAE、∠B,∠C之间的数量关系为___________;
(3)如图3,延长AC到点F,∠CAE和∠BCF的角平分线交于点G,求∠G的度数.
参考答案
知识回顾:与它不相邻的两个内角的和,360
同步练习
选择题:CCCCCC
填空题:1.360;2.48°;3.75°;4.70°;5.30°或75°;6.∠BPC=(∠BAD+∠ADC)
解答题:
解法一:连接 AD 并延长到点 E.
在△ABD 中,∠1 +∠B =∠3,
在△ACD 中,∠2 +∠C =∠4.
∵∠BDC =∠3 +∠4,∠BAC =∠1 +∠2,
∴∠BDC =∠BAC +∠B +∠C= 51° + 20° + 30° = 101°.
解法二:延长 BD 交 AC 于点 E(或连接 CD 并延长交 AB 于 F)
在△ABE 中,∠1 =∠B +∠A,
在△ECD 中,∠BDC =∠1 +∠C.
∴∠BDC =∠A +∠B +∠C= 51° + 20° + 30° = 101°.
解法1 解法2
2.解:延长 BP 交 AC 于点 E,
则∠BPC,∠PEC 分别为△PCE,△ABE 的外角,
∴∠BPC=∠PEC+∠PCE,∠PEC=∠ABE+∠A.
∴∠PEC=∠BPC-∠PCE=150°-30°=120°.
∴∠A=∠PEC-∠ABE=120°-20°=100°.
3.解:(1)探究2结论:∠BOC=∠A,
理由如下:
∵BO和CO分别是∠ABC和∠ACD的角平分线,
∴∠1=∠ABC,∠2=∠ACD,
又∵∠ACD是△ABC的一外角,
∴∠ACD=∠A+∠ABC,
∴∠2=(∠A+∠ABC)=∠A+∠1,
∵∠2是△BOC的一外角,
∴∠BOC=∠2-∠1=∠A+∠1-∠1=∠A;
(2)探究3结论∠BOC=90°-∠A.
4.解:(1)∵∠B=40°,∠C=60°,∠BAC+∠B+∠C=180°,
∴∠BAC=80°,
∵AD平分∠BAC,
∴∠CAD=∠BAD=∠BAC=40°,
∵AE是△ABC的高,
∴∠AEC=90°,
∵∠C=60°,
∴∠CAE=90° 60°=30°,
∴∠DAE=∠CAD ∠CAE=10°;
(2)∵∠BAC+∠B+∠C=180°,
∴∠BAC=180° ∠B ∠C,
∵AD平分∠BAC,
∴∠CAD=∠BAD=∠BAC,
∵AE是△ABC的高,
∴∠AEC=90°,
∴∠CAE=90° ∠C,
∴∠DAE=∠CAD ∠CAE=∠BAC (90° ∠C)=(180° ∠B ∠C) 90°+∠C=∠C ∠B,
即∠DAE=(∠C ∠B).
故答案为:∠DAE=(∠C ∠B).
(3)设∠ACB=,
∵AE⊥BC,
∴∠EAC=90° ,∠BCF=180° ,
∵∠CAE和∠BCF的角平分线交于点G,
∴∠CAG=∠EAC=(90° )=45° ,
∠FCG=∠BCF=(180° )=90° ,
∵∠FCG=∠G+∠CAG,
∴∠G=∠FCG ∠CAG=90° (45° )=45°.
