2022-2023学年华东师大版九年级数学上册24.4解直角三角形 作业(word版含解析)
文档属性
| 名称 | 2022-2023学年华东师大版九年级数学上册24.4解直角三角形 作业(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-05 14:43:34 | ||
图片预览




文档简介
24.4解直角三角形
一、单选题
1.如图是长春市人民大街下穿隧道工程施工现场的一台起重机的示意图,该起重机的变幅索顶端记为点A,变幅索的底端记为点B,垂直地面,垂足为点D,,垂足为点C.设,下列关系式正确的是( )
A. B. C. D.
2.河堤横断面如图所示,堤高BC=10米,迎水坡AB的坡比为1:,则AC的长是( )
A.5米 B.10米 C.15米 D.10米
二、填空题
3.如图,某水库堤坝横断面迎水坡的坡角为 , ,堤坝高 ,则迎水坡面 的长度为
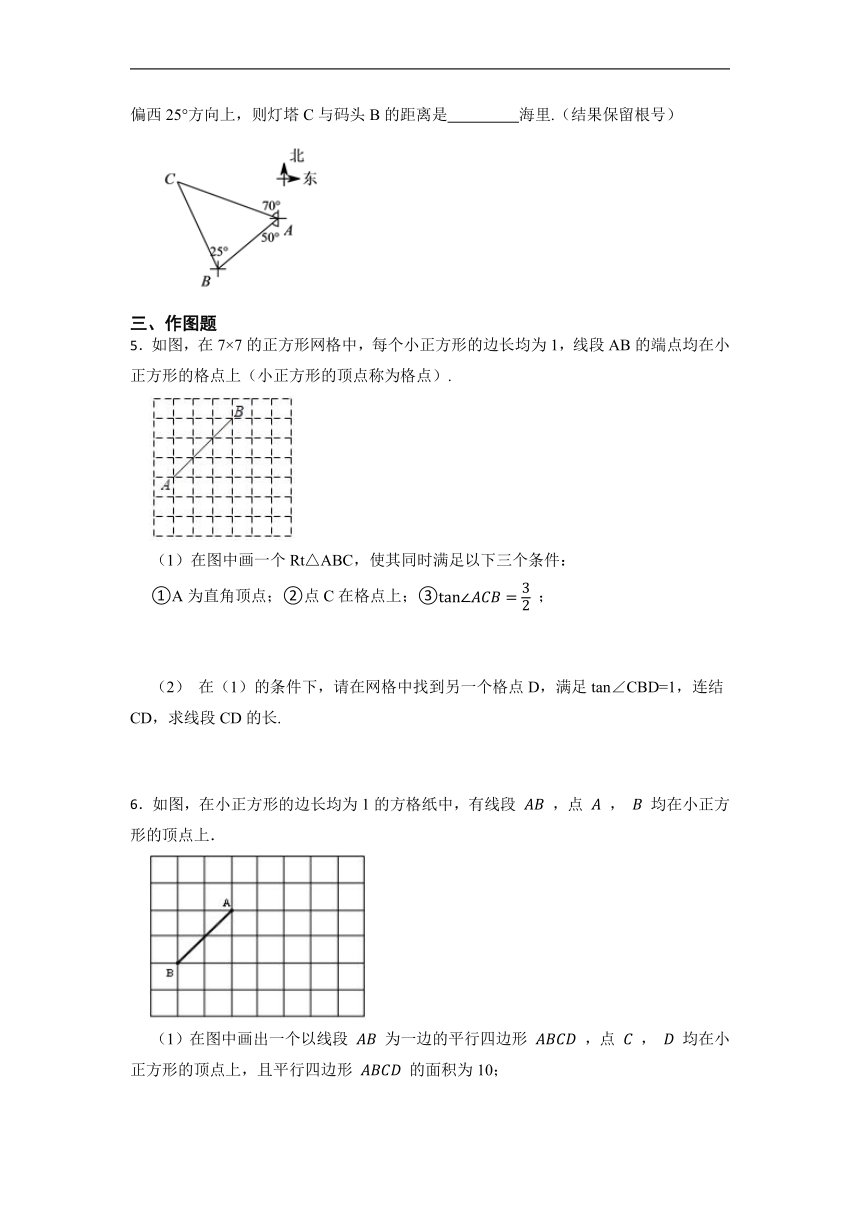
4.如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,2小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是 海里.(结果保留根号)
三、作图题
5.如图,在7×7的正方形网格中,每个小正方形的边长均为1,线段AB的端点均在小正方形的格点上(小正方形的顶点称为格点).
(1)在图中画一个Rt△ABC,使其同时满足以下三个条件:
①A为直角顶点;②点C在格点上;③ ;
(2) 在(1)的条件下,请在网格中找到另一个格点D,满足tan∠CBD=1,连结CD,求线段CD的长.
6.如图,在小正方形的边长均为1的方格纸中,有线段 ,点 , 均在小正方形的顶点上.
(1)在图中画出一个以线段 为一边的平行四边形 ,点 , 均在小正方形的顶点上,且平行四边形 的面积为10;
(2)在图中画一个钝角三角形 ,点 在小正方形的顶点上,且三角形 面积为4, .请直接写出 的长.
7.如图,在 的正方形网格中,每个小正方形的边长均为1,线段 、线段 的端点均在小正方形的项点上.
(1)在图中以 为边画 ,使点C在小正方形的顶点上,且 , ;
(2)在(1)的条件下,在图中画以 为边且面积为3的 ,使点D在小正方形的顶点上,且 ,连结 ,直接写出线段 的长.
四、解答题
8.某型号飞机的机翼形状如图所示,根据图中数据计算的长度(结果保留小数点后一位,).
9.某数学小组要测量学校路灯的顶部到地面的距离,他们借助皮尺、测角仅进行测量,测量结果如下:
测量项目 测量数据
从A处测得路灯顶部P的仰角
从D处测得路灯顶部P的仰角
测角仪到地面的距离
两次测量时测角仪之间的水平距离
计算路灯顶部到地面的距离约为多少米 (结果精确到0.1米.参考数据;)
10.如图,湖中一古亭,湖边一古柳,一沉静,一飘逸、碧波荡漾,相映成趣.某活动小组赏湖之余,为了测量古亭与古柳间的距离,在古柳A处测得古亭B位于北偏东60°,他们向南走50m到达D点,测得古亭B位于北偏东45°,求古亭与古柳之间的距离AB的长(参考数据:,,结果精确到1m).
11.今年入夏以来,松花江哈尔滨段水位不断下降,达到历史最低水位.一条船在松花江某水段自西向东沿直线航行,如图,在A处测得航标C在北偏东60°方向上.前进100米到达B处,又测得航标C在北偏东45°方向上.在以航标C为圆心,120米长为半径的圆形区域内有浅滩.如果这条船继续前进,是否有被浅滩阻碍的危险?(供考生参考的数据: ≈1.732)
五、综合题
12.如图,莲花山是大连著名的景点之一,游客可以从山底乘坐索道车到达山项,索速车运行的速度是1米/秒,小明要测量莲花山山顶白塔的高度,他在索道A处测得白塔底部B的仰角的为,测得白塔顶部C的仰角的为.索道车从A处运行到B处所用时间的为5分钟.
(1)索道车从A处运行到B处的距离约为 米;
(2)请你利用小明测量的数据,求白塔的高度(结果取整数).(参考数据:)
13.为积极响应党中央号召,推进乡村振兴,某地区对A,B两地间的公路进行改建.如图,A、B两地间有一座山,汽车原来从A地到B地需要途经C地沿折线ACB行驶.现开通隧道后,汽车可直接沿直线AB行驶.已知 千米, , .(结果精确到0.1千米,参考数据: , )
(1)开通隧道前,汽车从A地到B地大约要走多少千米?
(2)开通隧道后,汽车从A地到B地大约可以少走多少千米?
14.如图,一艘船正以 海里/小时的速度向正东航行,在A处看小岛C在船北偏东60°,继续航行1小时到达B处,此时看见小岛C在船的北偏东30°.
(1)求小岛C到航线AB的距离.
(2)已知以小岛C为中心周围20海里内为我军导弹部队军事演习的着弹危险区,问这艘船继续向东航行,是否有进入危险区的可能?
15.如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为30°,再往塔的方向前进50米至B处,测得仰角为60°.
(1)求证:AB=BD;
(2)求塔高CD.(小明的身高忽略不计,结果保留根号)
答案解析部分
1.【答案】D
2.【答案】D
3.【答案】50
4.【答案】
5.【答案】(1)解:由题意,知 .
∵ ,
∴ .
如图,Rt△ABC即为所求:
(2)解:∵tan∠CBD=1,∴∠CBD=45°.
如图所示,点D和点D′即为所求:
∴
6.【答案】(1)解:在A的水平方向取一条长为5的线段 ,再取在B的水平方向取一条长为5的线段 ,四边形 即为所求.
(2)解:在A的水平方向取一条长为的线段 ,则 为钝角,
过 作 于 则
所以 即为所求.
此时:
7.【答案】(1)解:如图, 即为所求;
(2)解:如图, 即为所求,
8.【答案】解:如图,延长交的垂线于点,交于点,则四边形是矩形,
,
四边形是正方形,
,
,,
,
中,,
,
中,,
米.
9.【答案】解:如图:延长DA,交PE于点F,则DF⊥PE,
∵,
∴四边形ABCD是平行四边形,
∵AB⊥BC,
∴四边形ABCD是矩形,
同理:四边形CDFE是矩形;
∴,,
在直角△PDF中,有,
在直角△PAF中,有,
∴,
即,
∴,
解得:;
∴;
∴(米);
∴路灯顶部到地面的距离约为3.5米.
10.【答案】解:如图,过点作的垂直,交延长线于点,
由题意得:,
设,则,
在中,,
在中,,,
则,
解得,
则,
答:古亭与古柳之间的距离的长约为.
11.【答案】解:过C作CD⊥AB于D,设BD=x,
∵CD⊥AB且∠CBD=45°∴BD=CD=x
在Rt△ACD中,tan30°=
∴
解得x=50( +1)≈137
∵137>120,
故这条船继续前进,没有被浅滩阻碍的危险.
12.【答案】(1)300
(2)解:由题意可得:
而
∴
∴
所以白塔的高度约为米.
13.【答案】(1)解:如图,过点C作AB的垂线CD,垂足为D,
∵AB⊥CD,AC=40千米,∠A=30°,∠B=45°.
∴BD=CD= AC=20千米,
∴BC= CD=20 (千米),
∴AC+BC=40+20 ≈40+1.41×20=68.2(千米).
∴开通隧道前,汽车从A地到B地大约要走68.2千米;
(2)解:∵AD=AC cos30°=40× =20 (千米),
∴BD=CD= AC=40× =20(千米),
∴AB=AD+BD=20 +20≈20×1.73+20=54.6(千米).
∴汽车从A地到B地比原来少走的路程为:
AC+BC-AB=68.2-54.6=13.6(千米).
∴开通隧道后,汽车从A地到B地大约可以少走13.6千米.
14.【答案】(1)解:作CD⊥AB交AB于点D,
由题意可知:∠CAB=90°-60°=30°,∠CBD=90°-30°=60°
∴∠ACB=∠CBD-∠CAB=30°
∴∠CAB=∠ACB
∴AB=CB=
在Rt△CBD中,CD=CB sin∠CBD=
∴小岛C到航线AB的距离为16海里;
(2)解:∵CD=16<20
∴这艘船继续向东航行会有进入危险区的可能.
15.【答案】(1)证明:∵∠DAB=30°,∠DBC=∠A+∠ADB=60°,
∴∠A=∠ADB=30°,
∴BD=AB;
(2)解:∵BD=AB=50米,
在Rt△BCD中,∠C=90°,
∴sin∠DBC=,
∴DC=BD sin60°=50×=25(米),
答:该塔高为25米.
一、单选题
1.如图是长春市人民大街下穿隧道工程施工现场的一台起重机的示意图,该起重机的变幅索顶端记为点A,变幅索的底端记为点B,垂直地面,垂足为点D,,垂足为点C.设,下列关系式正确的是( )
A. B. C. D.
2.河堤横断面如图所示,堤高BC=10米,迎水坡AB的坡比为1:,则AC的长是( )
A.5米 B.10米 C.15米 D.10米
二、填空题
3.如图,某水库堤坝横断面迎水坡的坡角为 , ,堤坝高 ,则迎水坡面 的长度为
4.如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,2小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是 海里.(结果保留根号)
三、作图题
5.如图,在7×7的正方形网格中,每个小正方形的边长均为1,线段AB的端点均在小正方形的格点上(小正方形的顶点称为格点).
(1)在图中画一个Rt△ABC,使其同时满足以下三个条件:
①A为直角顶点;②点C在格点上;③ ;
(2) 在(1)的条件下,请在网格中找到另一个格点D,满足tan∠CBD=1,连结CD,求线段CD的长.
6.如图,在小正方形的边长均为1的方格纸中,有线段 ,点 , 均在小正方形的顶点上.
(1)在图中画出一个以线段 为一边的平行四边形 ,点 , 均在小正方形的顶点上,且平行四边形 的面积为10;
(2)在图中画一个钝角三角形 ,点 在小正方形的顶点上,且三角形 面积为4, .请直接写出 的长.
7.如图,在 的正方形网格中,每个小正方形的边长均为1,线段 、线段 的端点均在小正方形的项点上.
(1)在图中以 为边画 ,使点C在小正方形的顶点上,且 , ;
(2)在(1)的条件下,在图中画以 为边且面积为3的 ,使点D在小正方形的顶点上,且 ,连结 ,直接写出线段 的长.
四、解答题
8.某型号飞机的机翼形状如图所示,根据图中数据计算的长度(结果保留小数点后一位,).
9.某数学小组要测量学校路灯的顶部到地面的距离,他们借助皮尺、测角仅进行测量,测量结果如下:
测量项目 测量数据
从A处测得路灯顶部P的仰角
从D处测得路灯顶部P的仰角
测角仪到地面的距离
两次测量时测角仪之间的水平距离
计算路灯顶部到地面的距离约为多少米 (结果精确到0.1米.参考数据;)
10.如图,湖中一古亭,湖边一古柳,一沉静,一飘逸、碧波荡漾,相映成趣.某活动小组赏湖之余,为了测量古亭与古柳间的距离,在古柳A处测得古亭B位于北偏东60°,他们向南走50m到达D点,测得古亭B位于北偏东45°,求古亭与古柳之间的距离AB的长(参考数据:,,结果精确到1m).
11.今年入夏以来,松花江哈尔滨段水位不断下降,达到历史最低水位.一条船在松花江某水段自西向东沿直线航行,如图,在A处测得航标C在北偏东60°方向上.前进100米到达B处,又测得航标C在北偏东45°方向上.在以航标C为圆心,120米长为半径的圆形区域内有浅滩.如果这条船继续前进,是否有被浅滩阻碍的危险?(供考生参考的数据: ≈1.732)
五、综合题
12.如图,莲花山是大连著名的景点之一,游客可以从山底乘坐索道车到达山项,索速车运行的速度是1米/秒,小明要测量莲花山山顶白塔的高度,他在索道A处测得白塔底部B的仰角的为,测得白塔顶部C的仰角的为.索道车从A处运行到B处所用时间的为5分钟.
(1)索道车从A处运行到B处的距离约为 米;
(2)请你利用小明测量的数据,求白塔的高度(结果取整数).(参考数据:)
13.为积极响应党中央号召,推进乡村振兴,某地区对A,B两地间的公路进行改建.如图,A、B两地间有一座山,汽车原来从A地到B地需要途经C地沿折线ACB行驶.现开通隧道后,汽车可直接沿直线AB行驶.已知 千米, , .(结果精确到0.1千米,参考数据: , )
(1)开通隧道前,汽车从A地到B地大约要走多少千米?
(2)开通隧道后,汽车从A地到B地大约可以少走多少千米?
14.如图,一艘船正以 海里/小时的速度向正东航行,在A处看小岛C在船北偏东60°,继续航行1小时到达B处,此时看见小岛C在船的北偏东30°.
(1)求小岛C到航线AB的距离.
(2)已知以小岛C为中心周围20海里内为我军导弹部队军事演习的着弹危险区,问这艘船继续向东航行,是否有进入危险区的可能?
15.如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为30°,再往塔的方向前进50米至B处,测得仰角为60°.
(1)求证:AB=BD;
(2)求塔高CD.(小明的身高忽略不计,结果保留根号)
答案解析部分
1.【答案】D
2.【答案】D
3.【答案】50
4.【答案】
5.【答案】(1)解:由题意,知 .
∵ ,
∴ .
如图,Rt△ABC即为所求:
(2)解:∵tan∠CBD=1,∴∠CBD=45°.
如图所示,点D和点D′即为所求:
∴
6.【答案】(1)解:在A的水平方向取一条长为5的线段 ,再取在B的水平方向取一条长为5的线段 ,四边形 即为所求.
(2)解:在A的水平方向取一条长为的线段 ,则 为钝角,
过 作 于 则
所以 即为所求.
此时:
7.【答案】(1)解:如图, 即为所求;
(2)解:如图, 即为所求,
8.【答案】解:如图,延长交的垂线于点,交于点,则四边形是矩形,
,
四边形是正方形,
,
,,
,
中,,
,
中,,
米.
9.【答案】解:如图:延长DA,交PE于点F,则DF⊥PE,
∵,
∴四边形ABCD是平行四边形,
∵AB⊥BC,
∴四边形ABCD是矩形,
同理:四边形CDFE是矩形;
∴,,
在直角△PDF中,有,
在直角△PAF中,有,
∴,
即,
∴,
解得:;
∴;
∴(米);
∴路灯顶部到地面的距离约为3.5米.
10.【答案】解:如图,过点作的垂直,交延长线于点,
由题意得:,
设,则,
在中,,
在中,,,
则,
解得,
则,
答:古亭与古柳之间的距离的长约为.
11.【答案】解:过C作CD⊥AB于D,设BD=x,
∵CD⊥AB且∠CBD=45°∴BD=CD=x
在Rt△ACD中,tan30°=
∴
解得x=50( +1)≈137
∵137>120,
故这条船继续前进,没有被浅滩阻碍的危险.
12.【答案】(1)300
(2)解:由题意可得:
而
∴
∴
所以白塔的高度约为米.
13.【答案】(1)解:如图,过点C作AB的垂线CD,垂足为D,
∵AB⊥CD,AC=40千米,∠A=30°,∠B=45°.
∴BD=CD= AC=20千米,
∴BC= CD=20 (千米),
∴AC+BC=40+20 ≈40+1.41×20=68.2(千米).
∴开通隧道前,汽车从A地到B地大约要走68.2千米;
(2)解:∵AD=AC cos30°=40× =20 (千米),
∴BD=CD= AC=40× =20(千米),
∴AB=AD+BD=20 +20≈20×1.73+20=54.6(千米).
∴汽车从A地到B地比原来少走的路程为:
AC+BC-AB=68.2-54.6=13.6(千米).
∴开通隧道后,汽车从A地到B地大约可以少走13.6千米.
14.【答案】(1)解:作CD⊥AB交AB于点D,
由题意可知:∠CAB=90°-60°=30°,∠CBD=90°-30°=60°
∴∠ACB=∠CBD-∠CAB=30°
∴∠CAB=∠ACB
∴AB=CB=
在Rt△CBD中,CD=CB sin∠CBD=
∴小岛C到航线AB的距离为16海里;
(2)解:∵CD=16<20
∴这艘船继续向东航行会有进入危险区的可能.
15.【答案】(1)证明:∵∠DAB=30°,∠DBC=∠A+∠ADB=60°,
∴∠A=∠ADB=30°,
∴BD=AB;
(2)解:∵BD=AB=50米,
在Rt△BCD中,∠C=90°,
∴sin∠DBC=,
∴DC=BD sin60°=50×=25(米),
答:该塔高为25米.
