第13章轴对称全章学案(共12课时)
文档属性
| 名称 | 第13章轴对称全章学案(共12课时) |  | |
| 格式 | zip | ||
| 文件大小 | 753.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-02 17:03:45 | ||
图片预览




文档简介
2013年秋人教版八年级上册数学
第13章 轴对称全章学案
第一课时 13.1 轴对称(1)
一、学习目标
1、认识轴对称和轴对称图形,并能找出对称轴;
2、知道轴对称和轴对称图形的区别和联系。
二、温故知新(口答)
1、如图(1),平分,则=_______=______。
2、如图(2),△ ABD ≌ △ACD,AB与 AC是对应边。试说出这两个三角形的对应顶点和对应边。
观察上面两个图形,你能发现它们有什么共同的的特点吗 ?
三、自主探究 合作展示
探究(一)
自学课本,完成以下问题。
什么是轴对称图形?你能举几个轴对称图形的例子吗?
2、试一试:下面的图形是轴对称图形吗?如果是,指出它的对称轴。
(1) (2) (3) (4) (5)
探究(二)
自学课本,完成以下问题。
1、什么叫做两个图形成轴对称?你能举几个生活中两个图形成轴对称的例子吗?
下面给出的每幅图中的两个图案是轴对称的吗?如果是,试着找出它们的对称轴,并找出一对对称点.
探究(三)
问题:
成轴对称的两个图形全等吗?如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形全等吗?这两个图形对称吗?
归纳:
区别:轴对称图形指的是_____个图形沿一条直线折叠,直线两旁的部分能够互相_________。
轴对称指的是_____个图形沿一条直线折叠 ,这个图形能够与另一个图形_________。
联系:把成轴对称的两个图形看成一个整体,它就是一个_______________;把一个轴对称图形沿对称轴分成两个图形,这两个图形关于这条直线对称(简称轴对称)
四、双基检测
1、轴对称图形的对称轴的条数( )
A.只有1条 B.2条 C.3条 D.至少一条
2、下列图形中对称轴最多的是( )
A.圆 B.正方形 C.角 D.线段
3、如下图,从几何图形的性质考虑,哪一个与其他三个不同?请指出这个图形,并简述你的理由.
答:图形 ;理由是: .
4、标出下列图形中点A、B、C的对称点。
5、下列图形是否是轴对称图形,如果是,找出轴对称图形的所有对称轴。
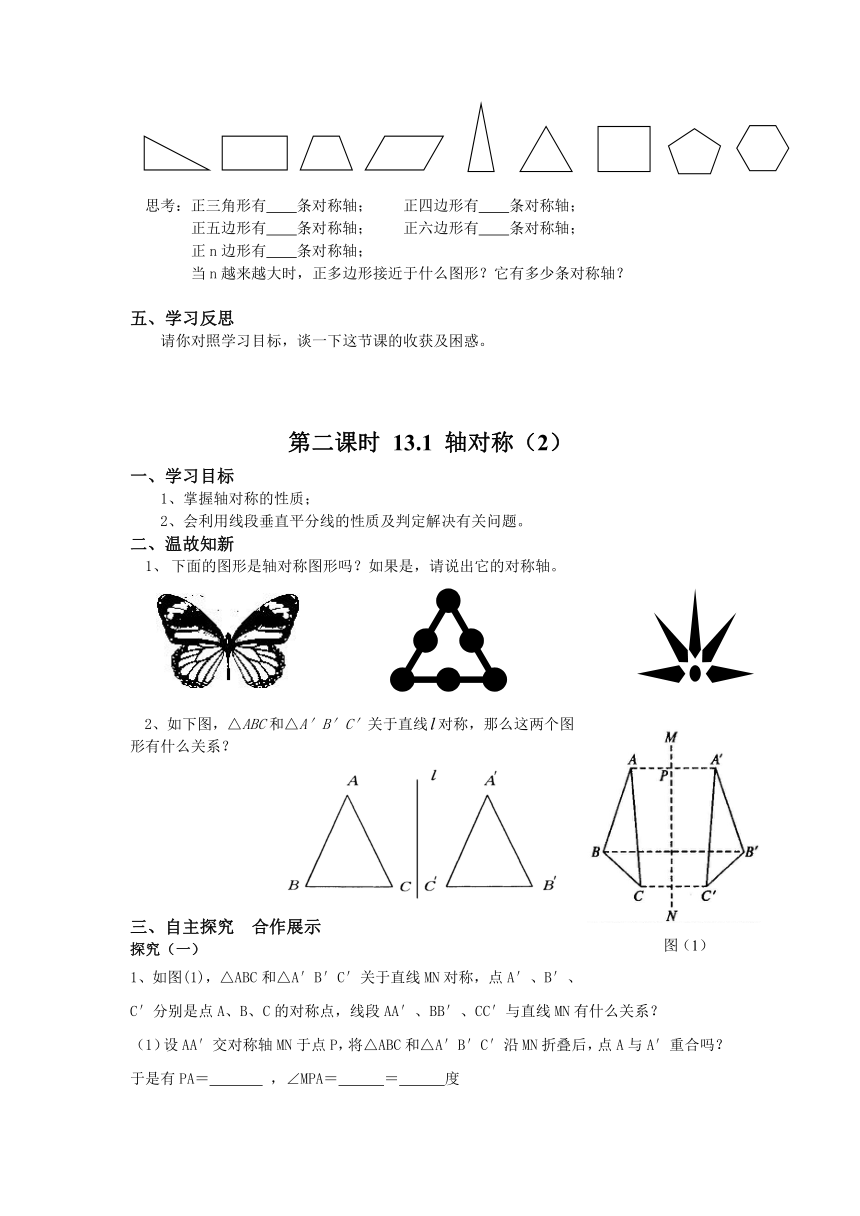
思考:正三角形有 条对称轴; 正四边形有 条对称轴;
正五边形有 条对称轴; 正六边形有 条对称轴;
正n边形有 条对称轴;
当n越来越大时,正多边形接近于什么图形?它有多少条对称轴?
五、学习反思
请你对照学习目标,谈一下这节课的收获及困惑。
第二课时 13.1 轴对称(2)
一、学习目标
1、掌握轴对称的性质;
2、会利用线段垂直平分线的性质及判定解决有关问题。
二、温故知新
下面的图形是轴对称图形吗?如果是,请说出它的对称轴。
2、如下图,△ABC和△A′B′C′关于直线对称,那么这两个图形有什么关系?
三、自主探究 合作展示
探究(一)
1、如图(1),△ABC和△A′B′C′关于直线MN对称,点A′、B′、C′分别是点A、B、C的对称点,线段AA′、BB′、CC′与直线MN有什么关系?
(1)设AA′交对称轴MN于点P,将△ABC和△A′B′C′沿MN折叠后,点A与A′重合吗?
于是有PA= ,∠MPA= = 度
(2)对于其他的对应点,如点B,B′;C,C′也有类似的情况吗?
(3)那么MN与线段AA′,BB′,CC′的连线有什么关系呢?
2、垂直平分线的定义:
经过线段 并且 这条线段的直线,叫做这条线段的垂直平分线.
3、轴对称的性质:
如果两个图形关于某条直线对称,那么 是任何一对对应点所连线段的 。
类似地,轴对称图形的对称轴,是任何一对对应点所连线段的 。
探究(二)
1、作出线段AB,过AB中点作AB的垂直平分线,在上取P1、P2、P3…,连结AP1、AP2、BP1、BP2、CP1、CP2…
2、作好图后,用直尺量出AP1、AP2、BP1、BP2、CP1、CP2…讨论发现什么样的规律.
总结线段垂直平分线的性质 :
3、你能利用判定两个三角形全等的方法证明这个性质吗?
如图(2),直线,垂足是,点在上。
求证:
探究(三)
作线段AB,取其中点P,过P作,在上取点P1、P2,连结AP1、AP2、BP1、BP2.会有哪些可能?要使L与AB垂直,AP1、AP2、BP1、BP2应满足什么条件?由此你得到什么结论?
你能证明这个结论吗?
新知应用:
例题:如图(3),在△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为13cm,求△ABC的周长。
例题反思:
四、双基检测
1、点P是△ABC中边AB的垂直平分线上的点,则一定有( )
A. PB=PC B.PA=PC C.PA=PB D.点P到∠ABC的两边距离相等
2、下列说法错误的是( )
A. D、E是线段AB的垂直平分线上的两点,则 AD=BD,AE=BE
B.若AD=BD,AE=BE,则直线DE是线段AB的垂直平分线
C.若PA=PB,则点P在线段AB的垂直平分线上
D.若PA=PB,则过点P的直线是线段AB的垂直平分线
3、如图(4),AB=AC,MB=MC.直线AM是线段BC的垂直平分线吗?
五、学习反思
请你对照学习目标,谈一下这节课的收获及困惑。
第三课时 13.1 轴对称(3)
一、学习目标
1、会依据轴对称的性质找出两个图形成轴对称及轴对称图形的对称轴;
2、掌握作出轴对称图形的对称轴的方法,即线段垂直平分线的尺规作图。
二、温故知新(口答)
1、下面的图形是轴对称图形吗?如果是,请说出它的对称轴。
2、如果两个图形关于某条直线对称,那么对称轴是任何一对 所连
的 线.
3、与一条线段两个端点距离相等的点,在这条线段的 上。
三、自主探究 合作展示
【问题】
如果我们感觉两个图形是成轴对称的,你准备用什么方法去验证?
两个成轴对称的图形,不经过折叠,你有什么方法画出它的对称轴?
归纳:
作轴对称图形的对称轴的方法是:找到一对 ,作出连接它们的 的 线,就可以得到这两个图形的对称轴.
【新知应用】
例题1:如图(1),点A和点B关于某条直线成轴对称,
你能作出这条直线吗?
1、请同学们按照以下作法在图(1)中完成作图。
作法:
(1)分别以点A、B为圆心,以大于AB的长为半径作弧,两弧相交于C和D两点;
(2)作直线CD.
直线CD即为所求的直线.
2、思考:(1)在上述作法中,为什么要以“大于AB的长”为半径作弧?
(2)在上面作法的基础上,连接AB, 直线CD是线段AB的垂直平分线吗?并说明理由.
例题反思:
例题2:如图(2),在五角星上作出它的一条对称轴。
例题反思:
四、双基检测
1、如图(3),下面的虚线中,哪些是图形的对称轴,哪些不是?
2、如图(4),画出图形的一条对称轴,和同学比较一下,你们画的对称轴一样吗?
3、如图(5),角是轴对称图形吗?如果是,画出它的对称轴。
4、如图(6),与图形A成轴对称的是哪个图形?画出它们的对称轴.
五、学习反思
请你对照学习目标,谈一下这节课的收获及困惑。
第四课时 13.2.1 作轴对称图形(1)
一、学习目标
1、认识轴对称图形,探索并了解它的基本性质;
2、能够按要求作出简单平面图形经过一次对称后的图形;
3、能利用轴对称进行图案设计。
二、温故知新(口答)
1、什么是轴对称图形?
2、请画出下列图形的对称轴。
三、自主探究 合作展示
探究(一)
自学:认真阅读教材的四辐图。
1、操作:自己动手在纸上画一个图案,将这张纸折叠,描图,再打开纸,看看你得到了什么?改变折痕的位置再试一次,你又得到了什么?
2、归纳:
(1)由一个平面图形可以得到它关于一条直线成轴对称的图形,这个图形与原图形
的 、 完全相同;
(2)新图形上的每一点,都是原图形上的某一点关于直线的 点;
(3)连接任意一对对应点的线段被对称轴 。
探究(二)
1、请同学们尝试解决以下问题;
如图(1),实线所构成的图形为已知图形,虚线为对称轴,请画出已知图形的轴对称图形。
问题:(1)你可以通过什么方法来验证你画的是否正确?
(2)和其他同学比较一下,你的方法是最简单的吗?
2、如图(2),已知点A和直线,试画出点A关于直线的对称点A′。
A·
3、例题:如图(3)已知△ABC,直线,画出△ABC关于直线的对称图形。
例题反思:
四、双基检测
1、把下列图形补成关于对称的图形。
2、小明在平面镜中看到身后墙上钟表显示的时间是12:15,这时的实际时间应该是 。
3、为美化校园,学校准备在一块圆形空地上建花坛,现征集设计方案,要求设计的图案由圆、三角形、矩形组成(三种几何图案的个数不限),并且使整个圆形场地成轴对称图形,请你画出你的设计方案.
五、学习反思
请你对照学习目标,谈一下这节课的收获及困惑。
第五课时 13.2.1 作轴对称图形(2)
一、学习目标
1、能够按要求作出简单平面图形经过轴对称后的图形;
2、能够用轴对称的知识解决生活中的实际问题。
二、温故知新
1、把下列图形补成关于对称的图形。
仔细观察第三个图形,你能尽可能多的从图中找出一些线段之间的关系吗?
三、自主探究 合作展示
探究(一)
如图(1).要在燃气管道上修建一个泵站,分别向A、B两镇供气.泵站修在管道的什么地方,可使所用的输气管线最短?
2、请同学们任意取点探究,并完成下列表格。
3、通过以上探究,你发现什么规律吗?
4、根据你发现的规律,在图(2)中完成本题。
探究(二)
问题
为什么在P点的位置修建泵站,就能使所用的输气管线最短呢?
四、双基检测
1、如图(3),在铁路的同侧有两个工厂A、B,要在路边建一个货场C,使A、B两厂到货场C的距离的和最小.问点C的位置如何选择?
2、如图(4),如果我们把台球桌做成等边三角形的形状,那么从AC的中点D处发出的球,能否依次经BC,AB两边反射后回到D处?如果认为不能,请说明理由;如果认为能,请作出球的运动路线。
3、如图(5),A为马厩,B为帐篷,牧马人某一天要从马厩牵出马,先到草地边某一处牧马,再到河边饮水,然后回到帐篷,请你帮他确定这一天的最短路线。
五、学习反思
请你对照学习目标,谈一下这节课的收获及困惑。
第六课时 13.2.2 用坐标表示轴对称
一、学习目标
1、能够经过探索利用坐标来表示轴对称;
2、掌握关于轴、轴对称的点的坐标特点。
二、温故知新
如图:(1)观察图(1)中两个圆脸有什么关系?
(2)若已知图(1)中圆脸右眼的坐标为(4,3),左眼
的坐标为(2,3),嘴角两个端点,右端点的坐标为(4,1),
左端点的坐标为(2,1).你能根据轴对称的性质写出左边圆
脸上左眼,右眼及嘴角两端点的坐标吗?
三、自主探究 合作展示
探究(一)
在如图(2)所示平面直角坐标系内画出下列已知点以及对称点,并把坐标填在表格中,你能发现坐标间有什么规律?
已知点
A(2,-3)
B(-1,2)
C(-6,-5)
D(0.5,1)
E(4,0)
关于轴对称的点
( )
( )
( )
( )
( )
关于轴对称的点
( )
( )
( )
( )
( )
2、归纳:点(,)关于轴对称的点的坐标是 ;
点(,)关于轴对称的点的坐标是
探究(二)
例题:
如图(3),四边形ABCD的四个顶点的坐标分别为A(-5,1),B(-2,1),C(-2,5),D(-5,4),分别作出四边形ABCD关于轴和轴对称的图形。
例题反思:
四、双基检测
1、分别写出下列各点关于轴和轴对称的点的坐标。
(3,6)
(-7,9)
(-3,-5)
(6,-1)
(0,10)
关于轴对称的点
关于轴对称的点
2、已知点(2a+b,-3a)与点(8,b+2).(1)若点与点关于轴对称,则a=_____;b=_______.
(2)若点与点关于轴对称,则a=_____;b=_______.
3、如图(4),△OBC关于轴对称,点A的坐标为(1,-2),标出点B的坐标.
3、如图(5),利用关于坐标轴对称的点的坐标的特点,分别作出与△ABC关于轴和轴对称的图形.
五、学习反思
请你对照学习目标,谈一下这节课的收获及困惑。
第七课时 13.3.1 等腰三角形(1)
一、学习目标
1、了解等腰三角形的概念,掌握等腰三角形的性质;
2、会运用等腰三角形的概念及性质解决相关问题。
二、温故知新
1、下列图形不一定是轴对称图形的是( ) A、圆 B、长方形 C、线段D、三角形
2、怎样的三角形是轴对称图形?答:
3、有两边相等的三角形叫 ,相等的两边叫 ,另一边叫 两腰的夹角叫 ,腰和底边的夹角叫
4、如图,在△ABC中,AB=AC,标出各部分名称
三、自主探究 合作展示
(一)操作、实践:
取一等腰三角形纸片,照图折叠,找出其中重合的线段和角,填入下表:
A A A
B C B(C) B D C
(1) (2) (3)
重合的线段
重合的角
【问题1】根据上表你能得出哪些结论?并将你的结论与同学交流。
【问题2】你能利用三角形全等的知识证明以上结论吗?
(二)【新知应用】
例1:填空:(1)如图(1)所示,根据等腰三角形性质定理在△ABC中,AB=AC时,
①∵AD⊥BC,∴∠_____ = ∠_____,____= ____.
② ∵AD是中线,∴____⊥____ ,∠_____ =∠_____.
③ ∵AD是角平分线,∴____ ⊥____ ,_____ =_____.
(2)等腰三角形一个底角为70°,它的顶角为______.
(3)等腰三角形一个角为70°,它的另外两个角为
例2:如图(2)所示,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.
分析:根据等边对等角的性质,我们可以得到∠A=______,∠ABC=______=______,再由∠BDC=∠A+______,就可得到∠ABC=______=______=2______.再由三角形内角和为180°,就可求出△ABC的三个内角.
解:例题反思:
四、双基检测
1、在△ABC中,AB=AC,
(1)如果∠A=70°,则∠C=_________,∠B=___________
(2)如果∠A=90°,则∠B=_________,∠C=___________
(3)如果有一个角等于120°,则其余两个角分别是多少度?
(4)如果有一个角等于55°,则其余两个角分别是多少度?
2、如图(3)所示,△ABC是等腰直角三角形(AB=AC,∠BAC=90°),AD是底边BC上的高,标出∠B、∠C、∠BAD、∠DAC的度数,图中有哪些相等线段?
3、如图(4),在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数.
五、学习反思
请你对照学习目标,谈一下这节课的收获及困惑。
第八课时 13.3.1 等腰三角形(2)
一、学习目标
1、理解等腰三角形的判定方法;
2、会运用等腰三角形的概念及性质解决相关问题。
二、温故知新
1、等腰三角形的两边长分别为6,8,则周长为
2、等腰三角形的一个角为70°,则另外两个角的度数是
3、等腰三角形的一个角为120°则另外两个角的度数是
三、自主探究 合作展示
(一)【思考】
(1)如图(1),位于在海上A、B两处的两艘救生船接到O处遇险船只的报警,当时测得∠A=∠B.如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?
(2)我们把这个问题一般化,在一般的三角形中,如果有两个角相等,那么它们所对的边有什么关系?
已知:在△ABO中,∠A=∠B
求证:AO=AO
证明:
【归纳】等腰三角形的判定方法:如果一个三角形有两个角相等,那么这两个角所对的
也相等(简写成 )
(二)【新知应用】
1、求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
请同学们完成下列问题
(1)、已知:如图(2), 是△ABC的外角,∠1= ,AD∥
求证: .
分析:要证明AB=AC,可先证明∠B= ,因为∠1= ,所以可设法找出
∠B、∠C与∠1、∠2的关系.
(2)、请同学们完整的写出解题过程
证明:
例题反思:
2、如图(3),标杆AB的高为5米,为了将它固定,需要由它的中点C向地面上与点B距离相等的D、E两点拉两条绳子,使得D、B、E在一条直线上,量得DE=4米,绳子CD和CE要多长?
例题反思:
四、双基检测
1、把一张等腰三角形的纸片沿与底边平行的虚线裁剪后(如图(4)所示),你得到的三角形还是等腰三角形吗?为什么?
2、如图(5),∠A=36°,∠DBC=36°,∠C=72°,分别计算∠1、∠2的度数,并说明图中有哪些等腰三角形.
3、如图(6),把一张矩形的纸沿对角线折叠.重合部分是一个等腰三角形吗?为什么?
4、如图(7),AC和BD相交于点O,且AB∥DC,OA=OB,求证:OC=OD.
五、学习反思
请你对照学习目标,谈一下这节课的收获及困惑。
第九课时 13.3.2 等边三角形(1)
一、学习目标
1、了解等边三角形是特殊的等腰三角形;
2、理解等边三角形的性质与判定。
二、温故知新
1、在△ABC中,AB=AC,
(1)如果∠A=70°,则∠C=_________,∠B=___________;
(2)如果∠A=90°,则∠B=_________,∠C=___________;
(3)如果∠A=60°,则∠B=_________,∠C=___________。
2、在△ABC中,如果AB=AC=BC,则∠A=_________,∠B=___________,∠C=_________。
3、____________________________的三角形是等边三角形,等边三角形是一种特殊的________三角形。
三、自主探究 合作展示
【问题】1、把等腰三角形的性质用于等边三角形,能得到什么结论?
2、一个三角形满足什么条件就是等边三角形?
3、你认为有一个角等于60°的等腰三角形是等边三角形吗?如果是请说明理由。
【新知应用】
例题:如图(1),在△ABC的边AB、AC上分别截取AD=AE.△ADE是等边三角形吗?试说明理由.
变式:如图(2),如将上述条件改为作∠ADE=60°,点D、E分别在边AB、AC上,结论还成立吗?改为过边AB上点D作DE∥BC,交边AC于点E呢?
例题反思:
探究(三)
等边三角形三条中线相交于一点。请在图(3)中画出图形,找出图中所有的全等三角形,并选择其中一组全等三角形进行证明。
四、双基检测
1、等边三角形是轴对称图形吗?它有几条对称轴?它们分别是什么?
2、如图(4),等边三角形ABC中,AD是BC上的高,∠BDE=∠CDF=60°,图中有哪些与BD相等的线段?
3、已知:如图(5),△ABC是等边三角形,BD是中线,延长BC到E,使CE=CD.
求证:DB=DE.
五、学习反思
请你对照学习目标,谈一下这节课的收获及困惑。
第十课时13.3.2 等边三角形(2)
一、学习目标
1、理解含30°锐角的直角三角形的性质;
2、能利用含30°锐角的直角三角形的性质解决简单的实际问题。
二、温故知新(口答)
1、等边三角形三边 ,三个角都等于 ,
2、等边三角形是轴对称图形,它有 条对称轴,它的对称轴 。
三、自主探究 合作展示
探究(一)
1、如图(1),将两个含有30°角的三角形放在一起,你能借助这个图形,找到Rt△ABC的直角边BC与斜边AB之间的数量关系吗?
2、你能用所学的知识验证以上结论吗?
方法1:如图(2),△ABC是等边三角形,AD⊥BC于D,∠BAD= °,BD= BC= AB。
方法2:如图(3),△ABC中,延长BC到D使BD=AB,连接AD,则△ABD是 三角形,
BC= = 。
探究(二)
例题:如图(4)是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=7.4m,∠A=30°,立柱BC、DE要多长?
分析:观察图形可以发现在Rt△AED与Rt△ACB中,由于∠A=30°,所以DE= ,BC= ,又由D是AB的中点,所以DE= .
例题反思:
探究(三)
例题:如图(5),要把一块三角形的土地均匀分给甲、乙、丙三家农户去种植,如果∠C=90°,
∠A=30°,要使这三家农户所得土地的大小和形状都相同,请你试着分一分,在图上画出来.
例题反思:
四、双基检测
1、等腰三角形中,一腰上的高与底边的夹角为30°,则此三角形中腰与底边的关系( )
A、腰大于底边 B、腰小于底边
C、腰等于底边 D、不能确定
2、在Rt△ABC中,∠C=90度,∠A=30°,CD⊥AB于点D,AB=8cm,则BC= ,
BD= , AD=
3、如图(6),在△ABC 中∠C=90°,∠B=15°,AB的垂直平分线交BC于D,交AB于M,且BD=8㎝,求AC之长.
五、学习反思
请你对照学习目标,谈一下这节课的收获及困惑。
第十一课时 轴对称复习(1)
一、复习目标
1、认识轴对称、轴对称图形,理解并掌握轴对称的有关性质;
2、掌握简单图形之间的轴对称关系,能按照要求作出简单图形经过一次或两次轴对称后的图形;
3、了解线段的垂直平分线的概念,并掌握其性质;
4、能利用轴对称的性质解决简单的实际问题。
二、知识再现
例1 、如图(1), 判断下列图形是不是轴对称图形.
例题反思:
例2 、如图(2),判断每组图形是否关于某条直线成轴对称.
例题反思:
例3、 如图(3)所示,已知△ABC和直线MN.求作:△A′B′C′,使△A′B′C′和△ABC关于直线MN对称.(不要求写作法,只保留作图痕迹)
例题反思:
例4、 如图(4)所示,有一块三角形田地,AB=AC=10m,作AB的垂直平分线ED交AC于D,交AB于E,量得△BDC的周长为17m,请你替测量人员计算BC的长.
例题反思:
三、双基检测
1、一只小狗正在平面镜前欣赏自己的全身像,此时,它所看到的全身像是( )
2、如果O是线段AB的垂直平分线与AB的交点,那么 = .
3、如图(5)所示,AB=AC=12,BC=7,AB的垂直平分线交AB于D,交AC于E,求△BCE的周长.
4、某地有两所大学和两条相交叉的公路,如图(6)所示(点M,N表示大学,AO,BO表示公路).现计划修建一座物资仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等.
(1)你能确定仓库应该建在什么位置吗?在所给的图形中画出你的设计方案;
(2)阐述你设计的理由.
四、拓展提高
如图(7)所示的是一个在19×16的点阵图上画出的“中国结”,点阵的每行及每列之间的距离都是1,请你画出“中国结”的对称轴,并直接写出阴影部分的面积
五、学习反思
请你对照复习目标,谈一下这节课的收获及困惑。
第十二课时 轴对称复习(2)
一、复习目标
1、了解等腰三角形的有关概念,探索并掌握等腰三角形的性质和一个三角形是等腰三角形的条件;
2、了解等边三角形的概念并探索其性质;
3、理解含30°锐角的直角三角形的性质并能利用它解决简单的实际问题。
二、知识再现
例1: 已知等腰三角形的一个内角是110°,求另外两个角的度数;
已知等腰三角形的一个内角是40°,求另外两个角的度数.
例题反思:
例2:如果等腰三角形的三边长均为整数,且它的周长为10cm,那么它的三边长分别为 .
例题反思:
例3:如图(1)所示,在△ABC中,AB=AC=CD,AD=DB,求∠BAC的度数.
例题反思:
例4:如图(2)所示,B,C,D三点在一条直线上,△ABC和△ECD是等边三角形.求证BE=AD.
例题反思:
例5:如图(3)所示,在△ABC中,∠C=90°,∠BAC=60°,AB的垂直平分线交AB于D,交BC于E,若CE=3cm,求BE的长.
例题反思:
三、双基检测
1、等边三角形的两条中线所成的钝角的度数是( )
A.120° B.130° C.150° D.160°
2、如果等腰三角形一底角为α,那么( )
A.α≤45° B.0°<α<90° C.α≤90° D.90°<α<180°
3、等腰三角形一腰上的高与底边所成的角等于( )
A.顶角 B.顶角的一半 C.顶角的2倍 D.底角的一半
4、如图(4)所示,在△ABC中,BO平分∠ABC,CO平分∠ACB,MN∥BC,MN经过点O,若AB=12,AC=18,则△AMN的周长是( )
A.15 B.18 C.24 D.30
5、(1)如果等腰三角形的两边长分别是4cm,7cm,那么它的周长是 ;
(2)如果等腰三角形的两边长分别是5cm,10cm,则它的周长是 .
6、如图(5)所示,∠1=∠2,BD=CD,试证明△ABC是等腰三角形.
四、拓展提高
(2008·安徽)已知:点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.
O
如图(6),若点O在边BC上,求证:AB=AC;
如图(7),若点O在△ABC的内部,求证:AB=AC;
若点O在△ABC的外部,AB=AC成立吗?请画图表示。
五、学习反思
请你对照复习目标,谈一下这节课的收获及困惑。
第13章 轴对称全章学案
第一课时 13.1 轴对称(1)
一、学习目标
1、认识轴对称和轴对称图形,并能找出对称轴;
2、知道轴对称和轴对称图形的区别和联系。
二、温故知新(口答)
1、如图(1),平分,则=_______=______。
2、如图(2),△ ABD ≌ △ACD,AB与 AC是对应边。试说出这两个三角形的对应顶点和对应边。
观察上面两个图形,你能发现它们有什么共同的的特点吗 ?
三、自主探究 合作展示
探究(一)
自学课本,完成以下问题。
什么是轴对称图形?你能举几个轴对称图形的例子吗?
2、试一试:下面的图形是轴对称图形吗?如果是,指出它的对称轴。
(1) (2) (3) (4) (5)
探究(二)
自学课本,完成以下问题。
1、什么叫做两个图形成轴对称?你能举几个生活中两个图形成轴对称的例子吗?
下面给出的每幅图中的两个图案是轴对称的吗?如果是,试着找出它们的对称轴,并找出一对对称点.
探究(三)
问题:
成轴对称的两个图形全等吗?如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形全等吗?这两个图形对称吗?
归纳:
区别:轴对称图形指的是_____个图形沿一条直线折叠,直线两旁的部分能够互相_________。
轴对称指的是_____个图形沿一条直线折叠 ,这个图形能够与另一个图形_________。
联系:把成轴对称的两个图形看成一个整体,它就是一个_______________;把一个轴对称图形沿对称轴分成两个图形,这两个图形关于这条直线对称(简称轴对称)
四、双基检测
1、轴对称图形的对称轴的条数( )
A.只有1条 B.2条 C.3条 D.至少一条
2、下列图形中对称轴最多的是( )
A.圆 B.正方形 C.角 D.线段
3、如下图,从几何图形的性质考虑,哪一个与其他三个不同?请指出这个图形,并简述你的理由.
答:图形 ;理由是: .
4、标出下列图形中点A、B、C的对称点。
5、下列图形是否是轴对称图形,如果是,找出轴对称图形的所有对称轴。
思考:正三角形有 条对称轴; 正四边形有 条对称轴;
正五边形有 条对称轴; 正六边形有 条对称轴;
正n边形有 条对称轴;
当n越来越大时,正多边形接近于什么图形?它有多少条对称轴?
五、学习反思
请你对照学习目标,谈一下这节课的收获及困惑。
第二课时 13.1 轴对称(2)
一、学习目标
1、掌握轴对称的性质;
2、会利用线段垂直平分线的性质及判定解决有关问题。
二、温故知新
下面的图形是轴对称图形吗?如果是,请说出它的对称轴。
2、如下图,△ABC和△A′B′C′关于直线对称,那么这两个图形有什么关系?
三、自主探究 合作展示
探究(一)
1、如图(1),△ABC和△A′B′C′关于直线MN对称,点A′、B′、C′分别是点A、B、C的对称点,线段AA′、BB′、CC′与直线MN有什么关系?
(1)设AA′交对称轴MN于点P,将△ABC和△A′B′C′沿MN折叠后,点A与A′重合吗?
于是有PA= ,∠MPA= = 度
(2)对于其他的对应点,如点B,B′;C,C′也有类似的情况吗?
(3)那么MN与线段AA′,BB′,CC′的连线有什么关系呢?
2、垂直平分线的定义:
经过线段 并且 这条线段的直线,叫做这条线段的垂直平分线.
3、轴对称的性质:
如果两个图形关于某条直线对称,那么 是任何一对对应点所连线段的 。
类似地,轴对称图形的对称轴,是任何一对对应点所连线段的 。
探究(二)
1、作出线段AB,过AB中点作AB的垂直平分线,在上取P1、P2、P3…,连结AP1、AP2、BP1、BP2、CP1、CP2…
2、作好图后,用直尺量出AP1、AP2、BP1、BP2、CP1、CP2…讨论发现什么样的规律.
总结线段垂直平分线的性质 :
3、你能利用判定两个三角形全等的方法证明这个性质吗?
如图(2),直线,垂足是,点在上。
求证:
探究(三)
作线段AB,取其中点P,过P作,在上取点P1、P2,连结AP1、AP2、BP1、BP2.会有哪些可能?要使L与AB垂直,AP1、AP2、BP1、BP2应满足什么条件?由此你得到什么结论?
你能证明这个结论吗?
新知应用:
例题:如图(3),在△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为13cm,求△ABC的周长。
例题反思:
四、双基检测
1、点P是△ABC中边AB的垂直平分线上的点,则一定有( )
A. PB=PC B.PA=PC C.PA=PB D.点P到∠ABC的两边距离相等
2、下列说法错误的是( )
A. D、E是线段AB的垂直平分线上的两点,则 AD=BD,AE=BE
B.若AD=BD,AE=BE,则直线DE是线段AB的垂直平分线
C.若PA=PB,则点P在线段AB的垂直平分线上
D.若PA=PB,则过点P的直线是线段AB的垂直平分线
3、如图(4),AB=AC,MB=MC.直线AM是线段BC的垂直平分线吗?
五、学习反思
请你对照学习目标,谈一下这节课的收获及困惑。
第三课时 13.1 轴对称(3)
一、学习目标
1、会依据轴对称的性质找出两个图形成轴对称及轴对称图形的对称轴;
2、掌握作出轴对称图形的对称轴的方法,即线段垂直平分线的尺规作图。
二、温故知新(口答)
1、下面的图形是轴对称图形吗?如果是,请说出它的对称轴。
2、如果两个图形关于某条直线对称,那么对称轴是任何一对 所连
的 线.
3、与一条线段两个端点距离相等的点,在这条线段的 上。
三、自主探究 合作展示
【问题】
如果我们感觉两个图形是成轴对称的,你准备用什么方法去验证?
两个成轴对称的图形,不经过折叠,你有什么方法画出它的对称轴?
归纳:
作轴对称图形的对称轴的方法是:找到一对 ,作出连接它们的 的 线,就可以得到这两个图形的对称轴.
【新知应用】
例题1:如图(1),点A和点B关于某条直线成轴对称,
你能作出这条直线吗?
1、请同学们按照以下作法在图(1)中完成作图。
作法:
(1)分别以点A、B为圆心,以大于AB的长为半径作弧,两弧相交于C和D两点;
(2)作直线CD.
直线CD即为所求的直线.
2、思考:(1)在上述作法中,为什么要以“大于AB的长”为半径作弧?
(2)在上面作法的基础上,连接AB, 直线CD是线段AB的垂直平分线吗?并说明理由.
例题反思:
例题2:如图(2),在五角星上作出它的一条对称轴。
例题反思:
四、双基检测
1、如图(3),下面的虚线中,哪些是图形的对称轴,哪些不是?
2、如图(4),画出图形的一条对称轴,和同学比较一下,你们画的对称轴一样吗?
3、如图(5),角是轴对称图形吗?如果是,画出它的对称轴。
4、如图(6),与图形A成轴对称的是哪个图形?画出它们的对称轴.
五、学习反思
请你对照学习目标,谈一下这节课的收获及困惑。
第四课时 13.2.1 作轴对称图形(1)
一、学习目标
1、认识轴对称图形,探索并了解它的基本性质;
2、能够按要求作出简单平面图形经过一次对称后的图形;
3、能利用轴对称进行图案设计。
二、温故知新(口答)
1、什么是轴对称图形?
2、请画出下列图形的对称轴。
三、自主探究 合作展示
探究(一)
自学:认真阅读教材的四辐图。
1、操作:自己动手在纸上画一个图案,将这张纸折叠,描图,再打开纸,看看你得到了什么?改变折痕的位置再试一次,你又得到了什么?
2、归纳:
(1)由一个平面图形可以得到它关于一条直线成轴对称的图形,这个图形与原图形
的 、 完全相同;
(2)新图形上的每一点,都是原图形上的某一点关于直线的 点;
(3)连接任意一对对应点的线段被对称轴 。
探究(二)
1、请同学们尝试解决以下问题;
如图(1),实线所构成的图形为已知图形,虚线为对称轴,请画出已知图形的轴对称图形。
问题:(1)你可以通过什么方法来验证你画的是否正确?
(2)和其他同学比较一下,你的方法是最简单的吗?
2、如图(2),已知点A和直线,试画出点A关于直线的对称点A′。
A·
3、例题:如图(3)已知△ABC,直线,画出△ABC关于直线的对称图形。
例题反思:
四、双基检测
1、把下列图形补成关于对称的图形。
2、小明在平面镜中看到身后墙上钟表显示的时间是12:15,这时的实际时间应该是 。
3、为美化校园,学校准备在一块圆形空地上建花坛,现征集设计方案,要求设计的图案由圆、三角形、矩形组成(三种几何图案的个数不限),并且使整个圆形场地成轴对称图形,请你画出你的设计方案.
五、学习反思
请你对照学习目标,谈一下这节课的收获及困惑。
第五课时 13.2.1 作轴对称图形(2)
一、学习目标
1、能够按要求作出简单平面图形经过轴对称后的图形;
2、能够用轴对称的知识解决生活中的实际问题。
二、温故知新
1、把下列图形补成关于对称的图形。
仔细观察第三个图形,你能尽可能多的从图中找出一些线段之间的关系吗?
三、自主探究 合作展示
探究(一)
如图(1).要在燃气管道上修建一个泵站,分别向A、B两镇供气.泵站修在管道的什么地方,可使所用的输气管线最短?
2、请同学们任意取点探究,并完成下列表格。
3、通过以上探究,你发现什么规律吗?
4、根据你发现的规律,在图(2)中完成本题。
探究(二)
问题
为什么在P点的位置修建泵站,就能使所用的输气管线最短呢?
四、双基检测
1、如图(3),在铁路的同侧有两个工厂A、B,要在路边建一个货场C,使A、B两厂到货场C的距离的和最小.问点C的位置如何选择?
2、如图(4),如果我们把台球桌做成等边三角形的形状,那么从AC的中点D处发出的球,能否依次经BC,AB两边反射后回到D处?如果认为不能,请说明理由;如果认为能,请作出球的运动路线。
3、如图(5),A为马厩,B为帐篷,牧马人某一天要从马厩牵出马,先到草地边某一处牧马,再到河边饮水,然后回到帐篷,请你帮他确定这一天的最短路线。
五、学习反思
请你对照学习目标,谈一下这节课的收获及困惑。
第六课时 13.2.2 用坐标表示轴对称
一、学习目标
1、能够经过探索利用坐标来表示轴对称;
2、掌握关于轴、轴对称的点的坐标特点。
二、温故知新
如图:(1)观察图(1)中两个圆脸有什么关系?
(2)若已知图(1)中圆脸右眼的坐标为(4,3),左眼
的坐标为(2,3),嘴角两个端点,右端点的坐标为(4,1),
左端点的坐标为(2,1).你能根据轴对称的性质写出左边圆
脸上左眼,右眼及嘴角两端点的坐标吗?
三、自主探究 合作展示
探究(一)
在如图(2)所示平面直角坐标系内画出下列已知点以及对称点,并把坐标填在表格中,你能发现坐标间有什么规律?
已知点
A(2,-3)
B(-1,2)
C(-6,-5)
D(0.5,1)
E(4,0)
关于轴对称的点
( )
( )
( )
( )
( )
关于轴对称的点
( )
( )
( )
( )
( )
2、归纳:点(,)关于轴对称的点的坐标是 ;
点(,)关于轴对称的点的坐标是
探究(二)
例题:
如图(3),四边形ABCD的四个顶点的坐标分别为A(-5,1),B(-2,1),C(-2,5),D(-5,4),分别作出四边形ABCD关于轴和轴对称的图形。
例题反思:
四、双基检测
1、分别写出下列各点关于轴和轴对称的点的坐标。
(3,6)
(-7,9)
(-3,-5)
(6,-1)
(0,10)
关于轴对称的点
关于轴对称的点
2、已知点(2a+b,-3a)与点(8,b+2).(1)若点与点关于轴对称,则a=_____;b=_______.
(2)若点与点关于轴对称,则a=_____;b=_______.
3、如图(4),△OBC关于轴对称,点A的坐标为(1,-2),标出点B的坐标.
3、如图(5),利用关于坐标轴对称的点的坐标的特点,分别作出与△ABC关于轴和轴对称的图形.
五、学习反思
请你对照学习目标,谈一下这节课的收获及困惑。
第七课时 13.3.1 等腰三角形(1)
一、学习目标
1、了解等腰三角形的概念,掌握等腰三角形的性质;
2、会运用等腰三角形的概念及性质解决相关问题。
二、温故知新
1、下列图形不一定是轴对称图形的是( ) A、圆 B、长方形 C、线段D、三角形
2、怎样的三角形是轴对称图形?答:
3、有两边相等的三角形叫 ,相等的两边叫 ,另一边叫 两腰的夹角叫 ,腰和底边的夹角叫
4、如图,在△ABC中,AB=AC,标出各部分名称
三、自主探究 合作展示
(一)操作、实践:
取一等腰三角形纸片,照图折叠,找出其中重合的线段和角,填入下表:
A A A
B C B(C) B D C
(1) (2) (3)
重合的线段
重合的角
【问题1】根据上表你能得出哪些结论?并将你的结论与同学交流。
【问题2】你能利用三角形全等的知识证明以上结论吗?
(二)【新知应用】
例1:填空:(1)如图(1)所示,根据等腰三角形性质定理在△ABC中,AB=AC时,
①∵AD⊥BC,∴∠_____ = ∠_____,____= ____.
② ∵AD是中线,∴____⊥____ ,∠_____ =∠_____.
③ ∵AD是角平分线,∴____ ⊥____ ,_____ =_____.
(2)等腰三角形一个底角为70°,它的顶角为______.
(3)等腰三角形一个角为70°,它的另外两个角为
例2:如图(2)所示,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.
分析:根据等边对等角的性质,我们可以得到∠A=______,∠ABC=______=______,再由∠BDC=∠A+______,就可得到∠ABC=______=______=2______.再由三角形内角和为180°,就可求出△ABC的三个内角.
解:例题反思:
四、双基检测
1、在△ABC中,AB=AC,
(1)如果∠A=70°,则∠C=_________,∠B=___________
(2)如果∠A=90°,则∠B=_________,∠C=___________
(3)如果有一个角等于120°,则其余两个角分别是多少度?
(4)如果有一个角等于55°,则其余两个角分别是多少度?
2、如图(3)所示,△ABC是等腰直角三角形(AB=AC,∠BAC=90°),AD是底边BC上的高,标出∠B、∠C、∠BAD、∠DAC的度数,图中有哪些相等线段?
3、如图(4),在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数.
五、学习反思
请你对照学习目标,谈一下这节课的收获及困惑。
第八课时 13.3.1 等腰三角形(2)
一、学习目标
1、理解等腰三角形的判定方法;
2、会运用等腰三角形的概念及性质解决相关问题。
二、温故知新
1、等腰三角形的两边长分别为6,8,则周长为
2、等腰三角形的一个角为70°,则另外两个角的度数是
3、等腰三角形的一个角为120°则另外两个角的度数是
三、自主探究 合作展示
(一)【思考】
(1)如图(1),位于在海上A、B两处的两艘救生船接到O处遇险船只的报警,当时测得∠A=∠B.如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?
(2)我们把这个问题一般化,在一般的三角形中,如果有两个角相等,那么它们所对的边有什么关系?
已知:在△ABO中,∠A=∠B
求证:AO=AO
证明:
【归纳】等腰三角形的判定方法:如果一个三角形有两个角相等,那么这两个角所对的
也相等(简写成 )
(二)【新知应用】
1、求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
请同学们完成下列问题
(1)、已知:如图(2), 是△ABC的外角,∠1= ,AD∥
求证: .
分析:要证明AB=AC,可先证明∠B= ,因为∠1= ,所以可设法找出
∠B、∠C与∠1、∠2的关系.
(2)、请同学们完整的写出解题过程
证明:
例题反思:
2、如图(3),标杆AB的高为5米,为了将它固定,需要由它的中点C向地面上与点B距离相等的D、E两点拉两条绳子,使得D、B、E在一条直线上,量得DE=4米,绳子CD和CE要多长?
例题反思:
四、双基检测
1、把一张等腰三角形的纸片沿与底边平行的虚线裁剪后(如图(4)所示),你得到的三角形还是等腰三角形吗?为什么?
2、如图(5),∠A=36°,∠DBC=36°,∠C=72°,分别计算∠1、∠2的度数,并说明图中有哪些等腰三角形.
3、如图(6),把一张矩形的纸沿对角线折叠.重合部分是一个等腰三角形吗?为什么?
4、如图(7),AC和BD相交于点O,且AB∥DC,OA=OB,求证:OC=OD.
五、学习反思
请你对照学习目标,谈一下这节课的收获及困惑。
第九课时 13.3.2 等边三角形(1)
一、学习目标
1、了解等边三角形是特殊的等腰三角形;
2、理解等边三角形的性质与判定。
二、温故知新
1、在△ABC中,AB=AC,
(1)如果∠A=70°,则∠C=_________,∠B=___________;
(2)如果∠A=90°,则∠B=_________,∠C=___________;
(3)如果∠A=60°,则∠B=_________,∠C=___________。
2、在△ABC中,如果AB=AC=BC,则∠A=_________,∠B=___________,∠C=_________。
3、____________________________的三角形是等边三角形,等边三角形是一种特殊的________三角形。
三、自主探究 合作展示
【问题】1、把等腰三角形的性质用于等边三角形,能得到什么结论?
2、一个三角形满足什么条件就是等边三角形?
3、你认为有一个角等于60°的等腰三角形是等边三角形吗?如果是请说明理由。
【新知应用】
例题:如图(1),在△ABC的边AB、AC上分别截取AD=AE.△ADE是等边三角形吗?试说明理由.
变式:如图(2),如将上述条件改为作∠ADE=60°,点D、E分别在边AB、AC上,结论还成立吗?改为过边AB上点D作DE∥BC,交边AC于点E呢?
例题反思:
探究(三)
等边三角形三条中线相交于一点。请在图(3)中画出图形,找出图中所有的全等三角形,并选择其中一组全等三角形进行证明。
四、双基检测
1、等边三角形是轴对称图形吗?它有几条对称轴?它们分别是什么?
2、如图(4),等边三角形ABC中,AD是BC上的高,∠BDE=∠CDF=60°,图中有哪些与BD相等的线段?
3、已知:如图(5),△ABC是等边三角形,BD是中线,延长BC到E,使CE=CD.
求证:DB=DE.
五、学习反思
请你对照学习目标,谈一下这节课的收获及困惑。
第十课时13.3.2 等边三角形(2)
一、学习目标
1、理解含30°锐角的直角三角形的性质;
2、能利用含30°锐角的直角三角形的性质解决简单的实际问题。
二、温故知新(口答)
1、等边三角形三边 ,三个角都等于 ,
2、等边三角形是轴对称图形,它有 条对称轴,它的对称轴 。
三、自主探究 合作展示
探究(一)
1、如图(1),将两个含有30°角的三角形放在一起,你能借助这个图形,找到Rt△ABC的直角边BC与斜边AB之间的数量关系吗?
2、你能用所学的知识验证以上结论吗?
方法1:如图(2),△ABC是等边三角形,AD⊥BC于D,∠BAD= °,BD= BC= AB。
方法2:如图(3),△ABC中,延长BC到D使BD=AB,连接AD,则△ABD是 三角形,
BC= = 。
探究(二)
例题:如图(4)是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=7.4m,∠A=30°,立柱BC、DE要多长?
分析:观察图形可以发现在Rt△AED与Rt△ACB中,由于∠A=30°,所以DE= ,BC= ,又由D是AB的中点,所以DE= .
例题反思:
探究(三)
例题:如图(5),要把一块三角形的土地均匀分给甲、乙、丙三家农户去种植,如果∠C=90°,
∠A=30°,要使这三家农户所得土地的大小和形状都相同,请你试着分一分,在图上画出来.
例题反思:
四、双基检测
1、等腰三角形中,一腰上的高与底边的夹角为30°,则此三角形中腰与底边的关系( )
A、腰大于底边 B、腰小于底边
C、腰等于底边 D、不能确定
2、在Rt△ABC中,∠C=90度,∠A=30°,CD⊥AB于点D,AB=8cm,则BC= ,
BD= , AD=
3、如图(6),在△ABC 中∠C=90°,∠B=15°,AB的垂直平分线交BC于D,交AB于M,且BD=8㎝,求AC之长.
五、学习反思
请你对照学习目标,谈一下这节课的收获及困惑。
第十一课时 轴对称复习(1)
一、复习目标
1、认识轴对称、轴对称图形,理解并掌握轴对称的有关性质;
2、掌握简单图形之间的轴对称关系,能按照要求作出简单图形经过一次或两次轴对称后的图形;
3、了解线段的垂直平分线的概念,并掌握其性质;
4、能利用轴对称的性质解决简单的实际问题。
二、知识再现
例1 、如图(1), 判断下列图形是不是轴对称图形.
例题反思:
例2 、如图(2),判断每组图形是否关于某条直线成轴对称.
例题反思:
例3、 如图(3)所示,已知△ABC和直线MN.求作:△A′B′C′,使△A′B′C′和△ABC关于直线MN对称.(不要求写作法,只保留作图痕迹)
例题反思:
例4、 如图(4)所示,有一块三角形田地,AB=AC=10m,作AB的垂直平分线ED交AC于D,交AB于E,量得△BDC的周长为17m,请你替测量人员计算BC的长.
例题反思:
三、双基检测
1、一只小狗正在平面镜前欣赏自己的全身像,此时,它所看到的全身像是( )
2、如果O是线段AB的垂直平分线与AB的交点,那么 = .
3、如图(5)所示,AB=AC=12,BC=7,AB的垂直平分线交AB于D,交AC于E,求△BCE的周长.
4、某地有两所大学和两条相交叉的公路,如图(6)所示(点M,N表示大学,AO,BO表示公路).现计划修建一座物资仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等.
(1)你能确定仓库应该建在什么位置吗?在所给的图形中画出你的设计方案;
(2)阐述你设计的理由.
四、拓展提高
如图(7)所示的是一个在19×16的点阵图上画出的“中国结”,点阵的每行及每列之间的距离都是1,请你画出“中国结”的对称轴,并直接写出阴影部分的面积
五、学习反思
请你对照复习目标,谈一下这节课的收获及困惑。
第十二课时 轴对称复习(2)
一、复习目标
1、了解等腰三角形的有关概念,探索并掌握等腰三角形的性质和一个三角形是等腰三角形的条件;
2、了解等边三角形的概念并探索其性质;
3、理解含30°锐角的直角三角形的性质并能利用它解决简单的实际问题。
二、知识再现
例1: 已知等腰三角形的一个内角是110°,求另外两个角的度数;
已知等腰三角形的一个内角是40°,求另外两个角的度数.
例题反思:
例2:如果等腰三角形的三边长均为整数,且它的周长为10cm,那么它的三边长分别为 .
例题反思:
例3:如图(1)所示,在△ABC中,AB=AC=CD,AD=DB,求∠BAC的度数.
例题反思:
例4:如图(2)所示,B,C,D三点在一条直线上,△ABC和△ECD是等边三角形.求证BE=AD.
例题反思:
例5:如图(3)所示,在△ABC中,∠C=90°,∠BAC=60°,AB的垂直平分线交AB于D,交BC于E,若CE=3cm,求BE的长.
例题反思:
三、双基检测
1、等边三角形的两条中线所成的钝角的度数是( )
A.120° B.130° C.150° D.160°
2、如果等腰三角形一底角为α,那么( )
A.α≤45° B.0°<α<90° C.α≤90° D.90°<α<180°
3、等腰三角形一腰上的高与底边所成的角等于( )
A.顶角 B.顶角的一半 C.顶角的2倍 D.底角的一半
4、如图(4)所示,在△ABC中,BO平分∠ABC,CO平分∠ACB,MN∥BC,MN经过点O,若AB=12,AC=18,则△AMN的周长是( )
A.15 B.18 C.24 D.30
5、(1)如果等腰三角形的两边长分别是4cm,7cm,那么它的周长是 ;
(2)如果等腰三角形的两边长分别是5cm,10cm,则它的周长是 .
6、如图(5)所示,∠1=∠2,BD=CD,试证明△ABC是等腰三角形.
四、拓展提高
(2008·安徽)已知:点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.
O
如图(6),若点O在边BC上,求证:AB=AC;
如图(7),若点O在△ABC的内部,求证:AB=AC;
若点O在△ABC的外部,AB=AC成立吗?请画图表示。
五、学习反思
请你对照复习目标,谈一下这节课的收获及困惑。
