北师大版数学九年级上册第三章概率的进一步认识 单元测试 (word版 含解析)
文档属性
| 名称 | 北师大版数学九年级上册第三章概率的进一步认识 单元测试 (word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 630.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-05 15:00:03 | ||
图片预览



文档简介
第三章 概率的进一步认识
一、选择题:(共10小题)
1.在某市组织的物理实验操作考试中,考试所用实验室共有24个测试位,分成6组,同组4个测试位各有一道相同试题,各组的试题不同,分别标记为A,B,C,D,E,F,考生从中随机抽取一道试题,则某个考生抽到试题A的概率为( )
A. B. C. D.
2.不透明的袋子中有两个小球,上面分别写着数字“1”“2”,除数字外两个小球无其他差别,从中随机摸出一个小球,记录其数字,放回并摇匀,再从中随机摸出一个小球,记录其数字,那么两次记录的数字之和为3的概率是( )
A. B. C. D.
3.一个不透明的盒子里有9个黄球和若干个红球,红球和黄球除颜色外其他完全相同,每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后再放回盒子,通过大量重复摸球试验后发现,摸到黄球的频率稳定在30%,那么估计盒子中红球的个数为( )
A.11 B.15 C.19 D.21
4.经过某十字路口的汽车,可能直行,也可能向左转或向右转,如果这三种可能性大小相同,则两辆汽车经过这个十字路口时,一辆向右转,辆向左转的概率是( )
A. B. C. D.
5.班长邀请A,B,C,D四位同学参加圆桌会议.如图,班长坐在⑤号座位,四位同学随机坐在①②③④四个座位,则A,B两位同学座位相邻的概率是( )
A. B. C. D.
6.一个不透明袋子中装有1个红球,2个绿球,除颜色外无其他差别.从中随机摸出一个球,然后放回摇匀,再随机摸出一个.下列说法中,错误的是( )
A.第一次摸出的球是红球,第二次摸出的球一定是绿球
B.第一次摸出的球是红球,第二次摸出的球不一定是绿球
C.第一次摸出的球是红球的概率是
D.两次摸出的球都是红球的概率是
7.如图,小李与小陈做猜拳游戏,规定每人每次至少要出一个手指,两人出拳的手指数之和为偶数时小李获胜,那么,小李获胜的概率为( )
A. B. C. D.
8.随着信息化的发展,二维码已经走进我们的日常生活,其图案主要由黑、白两种小正方形组成.现对由三个小正方形组成的“ ”进行涂色,每个小正方形随机涂成黑色或白色,恰好是两个黑色小正方形和一个白色小正方形的概率为( )
A. B. C. D.
9.从1,2,3,4四个数中随机选取两个不同的数,分别记为a,c,则关于x的一元二次方程有实数解的概率为( )
A. B. C. D.
10.某小组做“用频率估计概率”的试验时,绘出的某一结果出现的频率折线图,则符合这一结果的试验可能是( )
A.抛一枚硬币,出现正面朝上
B.掷一个正六面体的骰子,出现3点朝上
C.一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃
D.从一个装有2个红球1个黑球的袋子中任取一球,取到的是黑球
二、填空题(共5小题)
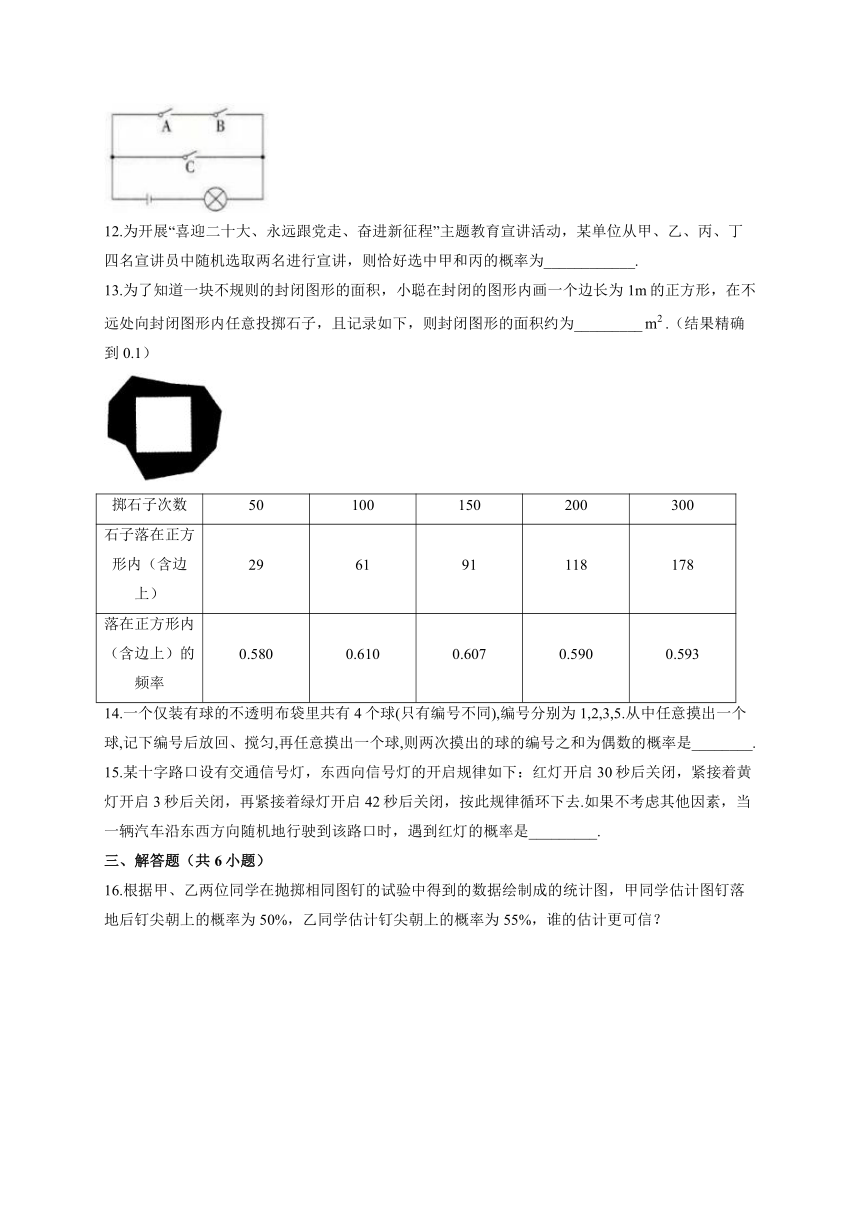
11.如图,电路图上有A、B、C3个开关和1个小灯泡,闭合开关C或同时闭合开关A、B都可以使小灯泡发亮.任意闭合其中的1个开关,小灯泡发亮的概率是___________.
12.为开展“喜迎二十大、永远跟党走、奋进新征程”主题教育宣讲活动,某单位从甲、乙、丙、丁四名宣讲员中随机选取两名进行宣讲,则恰好选中甲和丙的概率为____________.
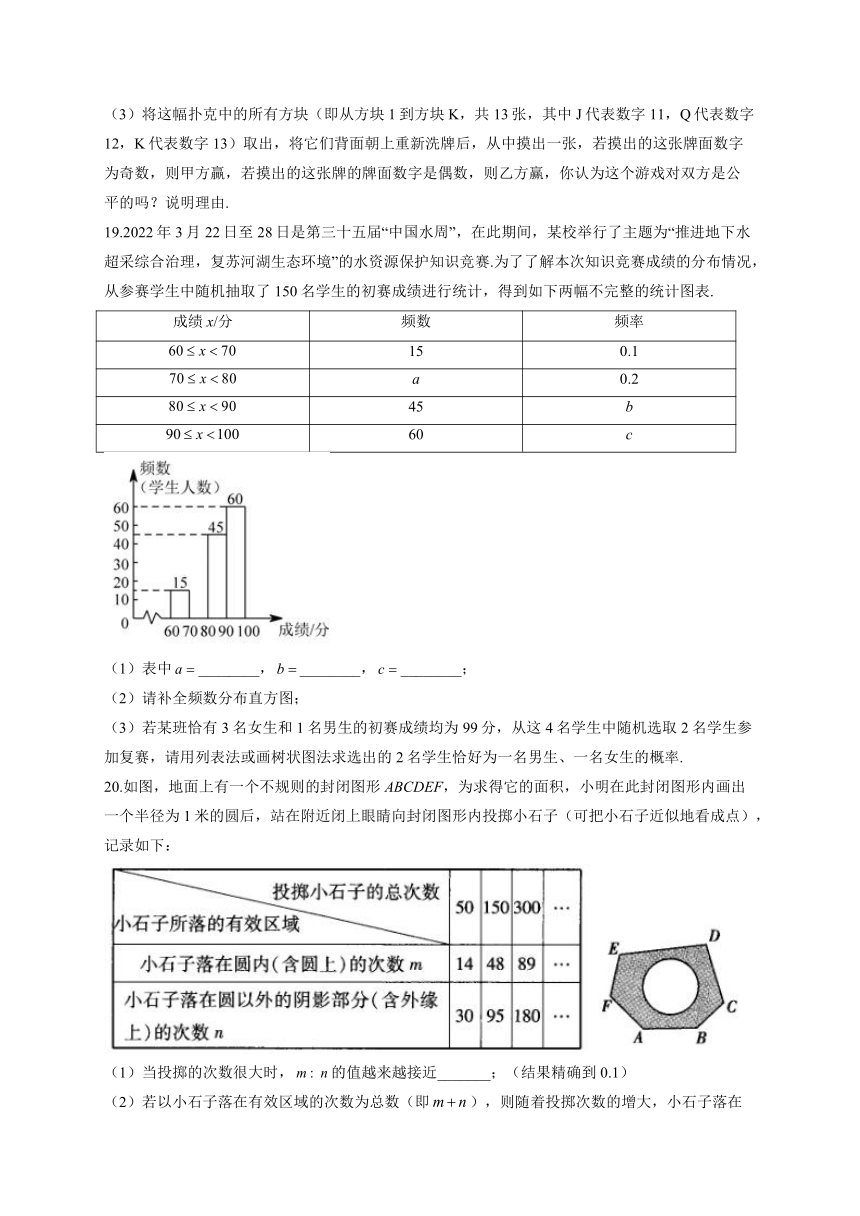
13.为了知道一块不规则的封闭图形的面积,小聪在封闭的图形内画一个边长为1m的正方形,在不远处向封闭图形内任意投掷石子,且记录如下,则封闭图形的面积约为_________.(结果精确到0.1)
掷石子次数 50 100 150 200 300
石子落在正方形内(含边上) 29 61 91 118 178
落在正方形内 (含边上)的频率 0.580 0.610 0.607 0.590 0.593
14.一个仅装有球的不透明布袋里共有4个球(只有编号不同),编号分别为1,2,3,5.从中任意摸出一个球,记下编号后放回、搅匀,再任意摸出一个球,则两次摸出的球的编号之和为偶数的概率是________.
15.某十字路口设有交通信号灯,东西向信号灯的开启规律如下:红灯开启30秒后关闭,紧接着黄灯开启3秒后关闭,再紧接着绿灯开启42秒后关闭,按此规律循环下去.如果不考虑其他因素,当一辆汽车沿东西方向随机地行驶到该路口时,遇到红灯的概率是_________.
三、解答题(共6小题)
16.根据甲、乙两位同学在抛掷相同图钉的试验中得到的数据绘制成的统计图,甲同学估计图钉落地后钉尖朝上的概率为50%,乙同学估计钉尖朝上的概率为55%,谁的估计更可信?
17.长白山国家级自然保护区、松花湖风景区和净月潭国家森林公园是吉林省著名的三个景区.甲、乙两人用抽卡片的方式决定一个自己要去的景区.他们准备了3张不透明的卡片,正面分别写上长白山、松花湖、净月潭.卡片除正面景区名称不同外其余均相同,将3张卡片正面向下洗匀,甲先从中随机抽取一张卡片,记下景区名称后正面向下放回,洗匀后乙再从中随机抽取一张卡片,请用画树状图或列表的方法,求两人都决定去长白山的概率.
18.从一副52张(没有大小王)的扑克中,每次抽出1张,然后放回洗匀再抽,在试验中得到下列表中部分数据试:
实验次数 40 80 120 160 200
出现方块的次数 11 18 a 40 49
出现方块的频率 27.5% 22.5% 25% 25% 24.5%
试验次数 240 280 320 360 400
出现方块的次数 63 68 80 91 100
出现方块的频率 26.25% 24.3% b 25.3% 25%
(1)填空:_________,_________.
(2)从上面的表中可以估计出现方块的概率是________.
(3)将这幅扑克中的所有方块(即从方块1到方块K,共13张,其中J代表数字11,Q代表数字12,K代表数字13)取出,将它们背面朝上重新洗牌后,从中摸出一张,若摸出的这张牌面数字为奇数,则甲方贏,若摸出的这张牌的牌面数字是偶数,则乙方赢,你认为这个游戏对双方是公平的吗?说明理由.
19.2022年3月22日至28日是第三十五届“中国水周”,在此期间,某校举行了主题为“推进地下水超采综合治理,复苏河湖生态环境”的水资源保护知识竞赛.为了了解本次知识竞赛成绩的分布情况,从参赛学生中随机抽取了150名学生的初赛成绩进行统计,得到如下两幅不完整的统计图表.
成绩x/分 频数 频率
15 0.1
a 0.2
45 b
60 c
(1)表中________,________,________;
(2)请补全频数分布直方图;
(3)若某班恰有3名女生和1名男生的初赛成绩均为99分,从这4名学生中随机选取2名学生参加复赛,请用列表法或画树状图法求选出的2名学生恰好为一名男生、一名女生的概率.
20.如图,地面上有一个不规则的封闭图形ABCDEF,为求得它的面积,小明在此封闭图形内画出一个半径为1米的圆后,站在附近闭上眼睛向封闭图形内投掷小石子(可把小石子近似地看成点),记录如下:
(1)当投掷的次数很大时,的值越来越接近_______;(结果精确到0.1)
(2)若以小石子落在有效区域的次数为总数(即),则随着投掷次数的增大,小石子落在圆内(含圆上)的频率稳定在_________;
(3)利用(2)中所得频率的稳定值,估计整个封闭图形ABCDEF的面积.(结果用表示)
21.为丰富校园文化生活,发展学生的兴趣与特长,促进学生全面发展.某中学团委组建了各种兴趣社团,为鼓励每个学生都参与到社团活动中,学生可以根据自己的爱好从美术、演讲、声乐、舞蹈、书法中选择其中1个社团.某班班主任对该班学生参加社团的情况进行调查统计,并绘制成如下两幅不完整的统计图.请根据统计图提供的信息完成下列各题:
(1)该班的总人数为_________人,并补全条形图(注:在所补小矩形上方标出人数);
(2)在该班团支部4人中,有1人参加美术社团,2人参加演讲社团,1人参加声乐社团如果该班班主任要从他们4人中任选2人作为学生会候选人,请利用树状图或列表法求选出的两人中恰好有1人参加美术社团、1人参加演讲社团的概率.
答案以及解析
1.答案:C
解析:总共有24道题,试题A共有4道,,故选:C.
2.答案:C
解析:由题意可知共有4种等可能的情况:,,,.其中和为3的情况有2种,故所求概率为.故选C.
3.答案:D
解析:设盒子中红球的个数为m,利用频率估计概率得到摸到黄球的概率为30%,则,解得.所以估计这个不透明的盒子中红球的个数为21.
4.答案:B
解析:画树状图如图所示:
这两辆汽车的行驶方向共有9种等可能的结果其中一辆向右转,
一辆向左转的结果有2种,
一辆向右转,一辆向左转的概率为.故选B.
5.答案:C
解析:根据题意,列表如下:
① ② ③ ④
① ①② ①③ ①④
② ②① ②④
③ ③① ③② ③④
④ ④① ④② ④③
由表格可知共有12种等可能的情况,其中①②,②①,②③,③②,③④,④③是相邻的座位,共6种,故A,B两位同学座位相邻的概率是.
6.答案:A
解析:选项A和B中的第一次已经确定是红球,所以第二次才是需要用概率计算的,因为放回,所以第二次袋子中有3个球,1个红球,2个绿球,所以第二次摸出红球的概率是,第二次摸出绿球的概率是,都是随机事件,故A选项“一定是绿球”是错误的,B选项正确;C选项第一次摸出红球的概率为,故正确;D选项是两步放回事件,可用树状图或列表法,列表如下:
红球 绿球① 绿球②
红球 红球,红球 绿球① 红球 绿球②, 红球
绿球① 红球, 绿球② 绿球①, 绿球① 绿球②, 绿球①
绿球② 红球, 绿球② 绿球①, 绿球② 绿球②, 绿球②
由上表可知,两次摸出的球都是红球的概率是.
7.答案:A
解析:画树状图如下:
∴共有25种等可能的结果,其中两人出拳的手指数之和为偶数的结果有13种,∴小李获胜的概率为.
8.答案:B
解析:根据题意可知共有如下8种情况,且每种情况出现的可能性相等.
有3个白色:;
有1个黑色:;
有2个黑色:;
有3个黑色:.
其中是两个黑色小正方形和一个白色小正方形的结果有3种,故所求概率为.
9.答案:C
解析:方程有实数解,
,.
画树状图如下:
由树状图可知,一共有12种等可能的结果,其中使方程有实数解,即使的结果有6种,关于x的一元二次方程有实数解的概率为,故选C.
10.答案:D
解析:由图可知,该试验的频率在0.2~0.4之间,稳定于0.35附近.
A.抛一枚硬币,出现正面朝上的概率为0.5,故A选项不符合题意;
B.掷一个正六面体的骰子,出现3点朝上的概率为,故B选项不符合题意;
C.一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃的概率为,故C选项不符合题意;
D.从一个装有2个红球1个黑球的袋子中任取一球,取到的是黑球的概率为,故D选项符合题意.
11.答案:
解析:任意闭合一个开关,有3种等可能结果,只闭合A或B小灯泡不发亮,只闭合C小灯泡发亮,所以任意闭合一个开关,小灯泡发亮的概率为.
12.答案:
解析:根据题意,列表如下:
甲 乙 丙 丁
甲 (乙,甲) (丙,甲) (丁,甲)
乙 (甲,乙) (丙,乙) (丁,乙)
丙 (甲,丙) (乙,丙) (丁,丙)
丁 (甲,丁) (乙,丁) (丙,丁)
由表格可知,共有12种等可能的情况,其中恰好选中甲和丙的情况有2种,故所求概率.
13.答案:1.7
解析:根据统计表,可得石子落在正方形内的概率约为0.593,设封闭图形的面积为x ,则有,解得.封闭图形的面积约为1.7.
14.答案:
解析:列表如下:
1 2 3 5
1 (1,1) (2,1) (3,1) (5,1)
2 (1,2) (2,2) (3,2) (5,2)
3 (1,3) (2,3) (3,3) (5,3)
4 (1,3) (2,3) (3,3) (5,3)
5 (1,5) (2,5) (3,5) (5,5)
由表可知,一共有16种等可能的结果,两次摸出的球的编号之和为偶数的结果有10种,∴两次摸出的球的编号之和为偶数的概率是.
15.答案:
解析:因为红灯亮30秒,黄灯亮3秒,绿灯亮42秒,所以.故答案为.
16.答案:乙同学的估计更可信.
因为乙同学的试验次数远远多于甲同学的试验次数,且从题中折线统计图上看,乙同学的试验数据基本趋于稳定,而甲同学的试验数据波动性较大,所以乙同学的估计更可信.
17.答案:
解析:将正面写有长白山、松花湖、净月潭的卡片依次用字母A,B,C表示.
方法一:画树状图如下.
由树状图可知,共有9种等可能的结果,其中甲、乙两人都决定去长白山的结果有1种,故所求概率为.
方法二:列表如下.
A B C
A (A,A) (A,B) (A,C)
B (B,A) (B,B) (B,C)
C (C,A) (C,B) (C,C)
由表格可知,共有9种等可能的结果,其中甲、乙两人都决定去长白山的结果有1种,故所求概率为.
18.答案:解:(1),.故答案为30,25%.
(2)从表中得出,出现方块的频率稳定在25%附近,故可以估计出现方块的概率为.故答案为.
(3)不公平.
因为在方块1到方块K共13张牌中,奇数有7个,偶数有6个,所以甲方赢的概率为,乙方赢的概率为,
由于,所以这个游戏对双方不公平.
19.答案:(1)30;0.3;0.4
(2)图见解析
(3)
解析:(2)补全频数分布直方图如图所示.
(3)根据题意,列表如下.
女 女2 女3 男
女1 (女1,女2) (女1,女3) (女1,男)
女2 (女2,女1) (女2,女3) (女2,男)
女3 (女3,女1) (女3,女2) (女3,男)
男 (男,女1) (男,女2) (男,女3)
由表可知共有12种等可能的情况,其中选出的2名学生恰好为1名男生、1名女生的情况有6种,故所求概率为.
20.答案:(1)0.5
,
,
,
…
所以当投掷的次数很大时,的值越来越接近0.5.
(2)
(3)设封闭图形ABCDEF的面积为a米 ,根据题意得,可解得,
所以封闭图形ABCDEF的面积约为3米 .
21.答案:(1)50,图见解析
(2)
解析:(1)50,补全条形图如图所示:
(2)解:树状图如下:
共有12种等可能的结果,而恰好有一人参加美术社团,一人参加演讲社团的结果有4种,
P(有一人参加美术社团,一人参加演讲社团).
一、选择题:(共10小题)
1.在某市组织的物理实验操作考试中,考试所用实验室共有24个测试位,分成6组,同组4个测试位各有一道相同试题,各组的试题不同,分别标记为A,B,C,D,E,F,考生从中随机抽取一道试题,则某个考生抽到试题A的概率为( )
A. B. C. D.
2.不透明的袋子中有两个小球,上面分别写着数字“1”“2”,除数字外两个小球无其他差别,从中随机摸出一个小球,记录其数字,放回并摇匀,再从中随机摸出一个小球,记录其数字,那么两次记录的数字之和为3的概率是( )
A. B. C. D.
3.一个不透明的盒子里有9个黄球和若干个红球,红球和黄球除颜色外其他完全相同,每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后再放回盒子,通过大量重复摸球试验后发现,摸到黄球的频率稳定在30%,那么估计盒子中红球的个数为( )
A.11 B.15 C.19 D.21
4.经过某十字路口的汽车,可能直行,也可能向左转或向右转,如果这三种可能性大小相同,则两辆汽车经过这个十字路口时,一辆向右转,辆向左转的概率是( )
A. B. C. D.
5.班长邀请A,B,C,D四位同学参加圆桌会议.如图,班长坐在⑤号座位,四位同学随机坐在①②③④四个座位,则A,B两位同学座位相邻的概率是( )
A. B. C. D.
6.一个不透明袋子中装有1个红球,2个绿球,除颜色外无其他差别.从中随机摸出一个球,然后放回摇匀,再随机摸出一个.下列说法中,错误的是( )
A.第一次摸出的球是红球,第二次摸出的球一定是绿球
B.第一次摸出的球是红球,第二次摸出的球不一定是绿球
C.第一次摸出的球是红球的概率是
D.两次摸出的球都是红球的概率是
7.如图,小李与小陈做猜拳游戏,规定每人每次至少要出一个手指,两人出拳的手指数之和为偶数时小李获胜,那么,小李获胜的概率为( )
A. B. C. D.
8.随着信息化的发展,二维码已经走进我们的日常生活,其图案主要由黑、白两种小正方形组成.现对由三个小正方形组成的“ ”进行涂色,每个小正方形随机涂成黑色或白色,恰好是两个黑色小正方形和一个白色小正方形的概率为( )
A. B. C. D.
9.从1,2,3,4四个数中随机选取两个不同的数,分别记为a,c,则关于x的一元二次方程有实数解的概率为( )
A. B. C. D.
10.某小组做“用频率估计概率”的试验时,绘出的某一结果出现的频率折线图,则符合这一结果的试验可能是( )
A.抛一枚硬币,出现正面朝上
B.掷一个正六面体的骰子,出现3点朝上
C.一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃
D.从一个装有2个红球1个黑球的袋子中任取一球,取到的是黑球
二、填空题(共5小题)
11.如图,电路图上有A、B、C3个开关和1个小灯泡,闭合开关C或同时闭合开关A、B都可以使小灯泡发亮.任意闭合其中的1个开关,小灯泡发亮的概率是___________.
12.为开展“喜迎二十大、永远跟党走、奋进新征程”主题教育宣讲活动,某单位从甲、乙、丙、丁四名宣讲员中随机选取两名进行宣讲,则恰好选中甲和丙的概率为____________.
13.为了知道一块不规则的封闭图形的面积,小聪在封闭的图形内画一个边长为1m的正方形,在不远处向封闭图形内任意投掷石子,且记录如下,则封闭图形的面积约为_________.(结果精确到0.1)
掷石子次数 50 100 150 200 300
石子落在正方形内(含边上) 29 61 91 118 178
落在正方形内 (含边上)的频率 0.580 0.610 0.607 0.590 0.593
14.一个仅装有球的不透明布袋里共有4个球(只有编号不同),编号分别为1,2,3,5.从中任意摸出一个球,记下编号后放回、搅匀,再任意摸出一个球,则两次摸出的球的编号之和为偶数的概率是________.
15.某十字路口设有交通信号灯,东西向信号灯的开启规律如下:红灯开启30秒后关闭,紧接着黄灯开启3秒后关闭,再紧接着绿灯开启42秒后关闭,按此规律循环下去.如果不考虑其他因素,当一辆汽车沿东西方向随机地行驶到该路口时,遇到红灯的概率是_________.
三、解答题(共6小题)
16.根据甲、乙两位同学在抛掷相同图钉的试验中得到的数据绘制成的统计图,甲同学估计图钉落地后钉尖朝上的概率为50%,乙同学估计钉尖朝上的概率为55%,谁的估计更可信?
17.长白山国家级自然保护区、松花湖风景区和净月潭国家森林公园是吉林省著名的三个景区.甲、乙两人用抽卡片的方式决定一个自己要去的景区.他们准备了3张不透明的卡片,正面分别写上长白山、松花湖、净月潭.卡片除正面景区名称不同外其余均相同,将3张卡片正面向下洗匀,甲先从中随机抽取一张卡片,记下景区名称后正面向下放回,洗匀后乙再从中随机抽取一张卡片,请用画树状图或列表的方法,求两人都决定去长白山的概率.
18.从一副52张(没有大小王)的扑克中,每次抽出1张,然后放回洗匀再抽,在试验中得到下列表中部分数据试:
实验次数 40 80 120 160 200
出现方块的次数 11 18 a 40 49
出现方块的频率 27.5% 22.5% 25% 25% 24.5%
试验次数 240 280 320 360 400
出现方块的次数 63 68 80 91 100
出现方块的频率 26.25% 24.3% b 25.3% 25%
(1)填空:_________,_________.
(2)从上面的表中可以估计出现方块的概率是________.
(3)将这幅扑克中的所有方块(即从方块1到方块K,共13张,其中J代表数字11,Q代表数字12,K代表数字13)取出,将它们背面朝上重新洗牌后,从中摸出一张,若摸出的这张牌面数字为奇数,则甲方贏,若摸出的这张牌的牌面数字是偶数,则乙方赢,你认为这个游戏对双方是公平的吗?说明理由.
19.2022年3月22日至28日是第三十五届“中国水周”,在此期间,某校举行了主题为“推进地下水超采综合治理,复苏河湖生态环境”的水资源保护知识竞赛.为了了解本次知识竞赛成绩的分布情况,从参赛学生中随机抽取了150名学生的初赛成绩进行统计,得到如下两幅不完整的统计图表.
成绩x/分 频数 频率
15 0.1
a 0.2
45 b
60 c
(1)表中________,________,________;
(2)请补全频数分布直方图;
(3)若某班恰有3名女生和1名男生的初赛成绩均为99分,从这4名学生中随机选取2名学生参加复赛,请用列表法或画树状图法求选出的2名学生恰好为一名男生、一名女生的概率.
20.如图,地面上有一个不规则的封闭图形ABCDEF,为求得它的面积,小明在此封闭图形内画出一个半径为1米的圆后,站在附近闭上眼睛向封闭图形内投掷小石子(可把小石子近似地看成点),记录如下:
(1)当投掷的次数很大时,的值越来越接近_______;(结果精确到0.1)
(2)若以小石子落在有效区域的次数为总数(即),则随着投掷次数的增大,小石子落在圆内(含圆上)的频率稳定在_________;
(3)利用(2)中所得频率的稳定值,估计整个封闭图形ABCDEF的面积.(结果用表示)
21.为丰富校园文化生活,发展学生的兴趣与特长,促进学生全面发展.某中学团委组建了各种兴趣社团,为鼓励每个学生都参与到社团活动中,学生可以根据自己的爱好从美术、演讲、声乐、舞蹈、书法中选择其中1个社团.某班班主任对该班学生参加社团的情况进行调查统计,并绘制成如下两幅不完整的统计图.请根据统计图提供的信息完成下列各题:
(1)该班的总人数为_________人,并补全条形图(注:在所补小矩形上方标出人数);
(2)在该班团支部4人中,有1人参加美术社团,2人参加演讲社团,1人参加声乐社团如果该班班主任要从他们4人中任选2人作为学生会候选人,请利用树状图或列表法求选出的两人中恰好有1人参加美术社团、1人参加演讲社团的概率.
答案以及解析
1.答案:C
解析:总共有24道题,试题A共有4道,,故选:C.
2.答案:C
解析:由题意可知共有4种等可能的情况:,,,.其中和为3的情况有2种,故所求概率为.故选C.
3.答案:D
解析:设盒子中红球的个数为m,利用频率估计概率得到摸到黄球的概率为30%,则,解得.所以估计这个不透明的盒子中红球的个数为21.
4.答案:B
解析:画树状图如图所示:
这两辆汽车的行驶方向共有9种等可能的结果其中一辆向右转,
一辆向左转的结果有2种,
一辆向右转,一辆向左转的概率为.故选B.
5.答案:C
解析:根据题意,列表如下:
① ② ③ ④
① ①② ①③ ①④
② ②① ②④
③ ③① ③② ③④
④ ④① ④② ④③
由表格可知共有12种等可能的情况,其中①②,②①,②③,③②,③④,④③是相邻的座位,共6种,故A,B两位同学座位相邻的概率是.
6.答案:A
解析:选项A和B中的第一次已经确定是红球,所以第二次才是需要用概率计算的,因为放回,所以第二次袋子中有3个球,1个红球,2个绿球,所以第二次摸出红球的概率是,第二次摸出绿球的概率是,都是随机事件,故A选项“一定是绿球”是错误的,B选项正确;C选项第一次摸出红球的概率为,故正确;D选项是两步放回事件,可用树状图或列表法,列表如下:
红球 绿球① 绿球②
红球 红球,红球 绿球① 红球 绿球②, 红球
绿球① 红球, 绿球② 绿球①, 绿球① 绿球②, 绿球①
绿球② 红球, 绿球② 绿球①, 绿球② 绿球②, 绿球②
由上表可知,两次摸出的球都是红球的概率是.
7.答案:A
解析:画树状图如下:
∴共有25种等可能的结果,其中两人出拳的手指数之和为偶数的结果有13种,∴小李获胜的概率为.
8.答案:B
解析:根据题意可知共有如下8种情况,且每种情况出现的可能性相等.
有3个白色:;
有1个黑色:;
有2个黑色:;
有3个黑色:.
其中是两个黑色小正方形和一个白色小正方形的结果有3种,故所求概率为.
9.答案:C
解析:方程有实数解,
,.
画树状图如下:
由树状图可知,一共有12种等可能的结果,其中使方程有实数解,即使的结果有6种,关于x的一元二次方程有实数解的概率为,故选C.
10.答案:D
解析:由图可知,该试验的频率在0.2~0.4之间,稳定于0.35附近.
A.抛一枚硬币,出现正面朝上的概率为0.5,故A选项不符合题意;
B.掷一个正六面体的骰子,出现3点朝上的概率为,故B选项不符合题意;
C.一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃的概率为,故C选项不符合题意;
D.从一个装有2个红球1个黑球的袋子中任取一球,取到的是黑球的概率为,故D选项符合题意.
11.答案:
解析:任意闭合一个开关,有3种等可能结果,只闭合A或B小灯泡不发亮,只闭合C小灯泡发亮,所以任意闭合一个开关,小灯泡发亮的概率为.
12.答案:
解析:根据题意,列表如下:
甲 乙 丙 丁
甲 (乙,甲) (丙,甲) (丁,甲)
乙 (甲,乙) (丙,乙) (丁,乙)
丙 (甲,丙) (乙,丙) (丁,丙)
丁 (甲,丁) (乙,丁) (丙,丁)
由表格可知,共有12种等可能的情况,其中恰好选中甲和丙的情况有2种,故所求概率.
13.答案:1.7
解析:根据统计表,可得石子落在正方形内的概率约为0.593,设封闭图形的面积为x ,则有,解得.封闭图形的面积约为1.7.
14.答案:
解析:列表如下:
1 2 3 5
1 (1,1) (2,1) (3,1) (5,1)
2 (1,2) (2,2) (3,2) (5,2)
3 (1,3) (2,3) (3,3) (5,3)
4 (1,3) (2,3) (3,3) (5,3)
5 (1,5) (2,5) (3,5) (5,5)
由表可知,一共有16种等可能的结果,两次摸出的球的编号之和为偶数的结果有10种,∴两次摸出的球的编号之和为偶数的概率是.
15.答案:
解析:因为红灯亮30秒,黄灯亮3秒,绿灯亮42秒,所以.故答案为.
16.答案:乙同学的估计更可信.
因为乙同学的试验次数远远多于甲同学的试验次数,且从题中折线统计图上看,乙同学的试验数据基本趋于稳定,而甲同学的试验数据波动性较大,所以乙同学的估计更可信.
17.答案:
解析:将正面写有长白山、松花湖、净月潭的卡片依次用字母A,B,C表示.
方法一:画树状图如下.
由树状图可知,共有9种等可能的结果,其中甲、乙两人都决定去长白山的结果有1种,故所求概率为.
方法二:列表如下.
A B C
A (A,A) (A,B) (A,C)
B (B,A) (B,B) (B,C)
C (C,A) (C,B) (C,C)
由表格可知,共有9种等可能的结果,其中甲、乙两人都决定去长白山的结果有1种,故所求概率为.
18.答案:解:(1),.故答案为30,25%.
(2)从表中得出,出现方块的频率稳定在25%附近,故可以估计出现方块的概率为.故答案为.
(3)不公平.
因为在方块1到方块K共13张牌中,奇数有7个,偶数有6个,所以甲方赢的概率为,乙方赢的概率为,
由于,所以这个游戏对双方不公平.
19.答案:(1)30;0.3;0.4
(2)图见解析
(3)
解析:(2)补全频数分布直方图如图所示.
(3)根据题意,列表如下.
女 女2 女3 男
女1 (女1,女2) (女1,女3) (女1,男)
女2 (女2,女1) (女2,女3) (女2,男)
女3 (女3,女1) (女3,女2) (女3,男)
男 (男,女1) (男,女2) (男,女3)
由表可知共有12种等可能的情况,其中选出的2名学生恰好为1名男生、1名女生的情况有6种,故所求概率为.
20.答案:(1)0.5
,
,
,
…
所以当投掷的次数很大时,的值越来越接近0.5.
(2)
(3)设封闭图形ABCDEF的面积为a米 ,根据题意得,可解得,
所以封闭图形ABCDEF的面积约为3米 .
21.答案:(1)50,图见解析
(2)
解析:(1)50,补全条形图如图所示:
(2)解:树状图如下:
共有12种等可能的结果,而恰好有一人参加美术社团,一人参加演讲社团的结果有4种,
P(有一人参加美术社团,一人参加演讲社团).
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
