5.1相交线垂线测试卷(附解析)
文档属性
| 名称 | 5.1相交线垂线测试卷(附解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 274.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-03 00:00:00 | ||
图片预览

文档简介
2013年10月3日第五章相交线提高测试卷 姓名
一.选择题(共12小题)
1.在直线AB上任取一点O,过点O作射线OC,OD,使OC⊥OD,当∠AOC=30°时,∠BOD的度数是( )
A. 60° B. 120° C. 60°或90° D. 60°或120°
2.两条相交直线所成的角中( )
A.必有一个钝角 B. 必有一个锐角
C.必有一个不是钝角 D. 必有两个锐角
3.如图,OA⊥OC,OB⊥OD,4位同学观察图形后分别说了自己的观点.甲:∠AOB=∠COD;乙:∠BOC+∠AOD=180°;丙:∠AOB+∠COD=90°;丁:图中小于平角的角有5个.其中正确的结论是( ) A.1个 B.2个 C. 3个 D.4个
4.三条直线两两相交于同一点时,对顶角有m对;交于不同三点时,对顶角有n对,则m与n的关系是( )
A. m=n B. m>n C. m<n D. m+n=10
5.下列图形中∠1与∠2是对顶角的是( )
A. B. C. D.
6.已知,OA⊥OC,且∠AOB:∠AOC=2:3,则∠BOC的度数为( )
A.30° B. 150° C. 30°或150° D. 90°
7.如图,在△ABC中,AC⊥BC,CD⊥AB,则图中能表示点到直线(或线段)的距离的线段有( )A.2条 B.3条 C.4条 D.5条
8.(1)延长射线OM; (2)平角是一条射线;(3)线段、射线都是直线的一部分;(4)锐角一定小于它的余角;(5)大于直角的角是钝角;(6)一个锐角的补角与这个锐角的余角的差是90°; (7)相等的两个角是对顶角; (8)若∠A+∠B+∠C=180°,则这三个角互补;(9)互为邻补角的两个角的平分线互相垂直.以上说法正确的有( )
A. 2个 B. 3个 C. ?4个 D. ?5个
9.在一个平面内,任意四条直线相交,交点的个数最多有( )
A. 7个 B. 6个 C. 5个 D. 4个
10.下列图形中,线段PQ的长表示点P到直线MN的距离是( )
A. B. C. D.
11.已知线段AB=10cm,点A,B到直线l的距离分别为6cm,4cm.符合条件的直线l有( )
A. 1条 B. 2条 C. 3条 D. 4条
12.下面四个图形中,∠1与∠2是对顶角的图形的个数是( )
A. 0 B. 1 C. 2 D. 3
二.填空题(共9小题)
13.观察下列图形,并阅读,图形下面的相关字.
两条直线相交最多有1个交点 三条直线相交最多有3个交点 四条直线相交最多有6个交点
则n条直线最多有 _________ 个交点.
14.如图:A、O、B在同一直线上,AB⊥OE,OC⊥OD,则图中互余的角共有 ___对.
15.图中有 _________ 对对顶角.
16.公园里准备修6条甬道,并在甬道交叉路口处设一个报亭,这样的报亭最多设 ________个.
17.(2006 南宁)如图,已知AB、CD相交于点O,OE⊥AB,∠EOC=28°,则∠AOD= _________ 度.
18题图 19题图
18.如图,OA⊥OB,∠BOC=30°,OD平分∠AOC,则∠BOD= _________ 度.
19.如图,已知直线AB、CD、EF相交于点O,∠1=95°,∠2=32°,则∠BOE= _________ 度.
20.如图,直线AB,CD相交于点O,∠AOC=54°,∠1比∠2大10°,则∠1= _________ 度;∠2= _________ 度.
21.如图,直线AB、CD相交于点O,OE⊥AB,O为垂足,如果∠EOD=38°,则∠AOC= _________ 度,∠COB= _________ 度.
19题图 20题图 21题图
三.解答题(共9小题)
22.已知点C在直线a外,点A在直线a上,且AC=2厘米.
(1)设d是点C到直线a的距离,求d的取值范围;
(2)若直线BD垂直于直线a,垂足为B.则直线BD与直线AC有怎样的位置关系,请画示意图表示(每种位置关系画一个示意图).
23.如图所示,OA丄OB,OC丄OD,OE为∠BOD的平分线,∠BOE=22°,求∠AOC的度数.
23题图 24题图 25题图
24.如图,直线BC与MN相交于点O,AO⊥BC,OE平分∠BON,若∠EON=20°,求∠AOM和∠NOC的度数.
25.如图①②所示,将两个相同三角板的两个直角顶点O重合在一起,像图①②那样放置.
(1)若∠BOC=60°,如图①,猜想∠AOD的度数;
(2)若∠BOC=70°,如图②,猜想∠AOD的度数;
(3)猜想∠AOD和∠BOC的关系,并写出理由.
26.观察下列各图,寻找对顶角(不含平角):
(1)如图a,图中共有 _________ 对对顶角;(2)如图b,图中共有 _________ 对对顶角;
(3)如图c,图中共有 _________ 对对顶角;(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可形成 _________ 对对顶角;
(5)若有2008条直线相交于一点,则可形成 _________ 对对顶角.
27.如图,直线AB、CD相交于O,OD平分∠AOF,OE⊥CD于点O,∠1=50°,求∠COB、∠BOF的度数.
28.如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD.
(1)图中除直角外,还有相等的角吗?请写出两对:① _________ ;② _________ .
(2)如果∠AOD=40°.①那么根据 _________ ,可得∠BOC= _________ 度.
②因为OP是∠BOC的平分线,所以∠COP=∠ _________ = _________ 度.
③求∠BOF的度数.
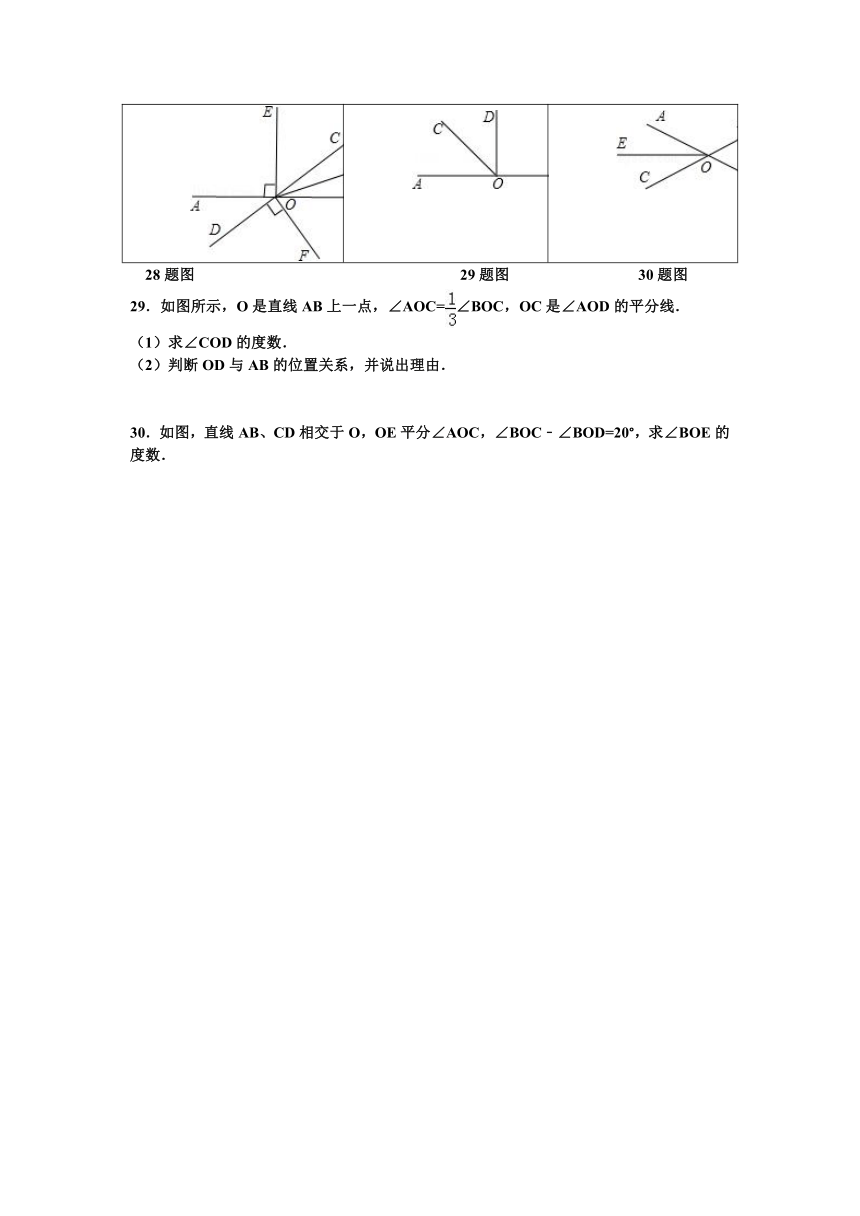
28题图 29题图 30题图
29.如图所示,O是直线AB上一点,∠AOC=∠BOC,OC是∠AOD的平分线.
(1)求∠COD的度数.
(2)判断OD与AB的位置关系,并说出理由.
30.如图,直线AB、CD相交于O,OE平分∠AOC,∠BOC﹣∠BOD=20°,求∠BOE的度数.
第五章5.1相交线提高测试卷参考答案与试题解析
一.选择题(共12小题)
1.在直线AB上任取一点O,过点O作射线OC,OD,使OC⊥OD,当∠AOC=30°时,∠BOD的度数是( )
A. 60° B. 120° C. 60°或90° D. 60°或120°
解答: 解:①当OC、OD在AB的一旁时,
∵OC⊥OD,∠COD=90°,∠AOC=30°,
∴∠BOD=180°﹣∠COD﹣∠AOC=60°;
②当OC、OD在AB的两旁时,
∵OC⊥OD,∠AOC=30°,
∴∠AOD=60°,
∴∠BOD=180°﹣∠AOD=120°.
故选D.
2.两条相交直线所成的角中( )
A. 必有一个钝角 B. 必有一个锐角
C. 必有一个不是钝角 D. 必有两个锐角
解答: 解:当两条直线互相垂直时所成的角都是直角,所以A、B、D都不对.
若都是钝角,则圆周角超过360°,
故选C.
3.如图,OA⊥OC,OB⊥OD,4位同学观察图形后分别说了自己的观点.甲:∠AOB=∠COD;乙:∠BOC+∠AOD=180°;丙:∠AOB+∠COD=90°;丁:图中小于平角的角有5个.其中正确的结论是( )
A. 1个 B. 2个 C. 3个 D. 4个
解答: 解:根据同角的余角相等可得,∠AOB=∠COD,而不会得出∠AOB+∠COD=90°,故甲正确,丙错误;
∠BOC+∠AOD=∠BOC+∠AOB+∠BOD=∠AOC+∠BOD=90°+90°=180°,故乙正确;
图中小于平角的角有∠COD,∠BOD,∠AOD,∠BOC,∠AOC,∠AOB六个,故丁错误.
正确的有两个,故选B.
4.三条直线两两相交于同一点时,对顶角有m对;交于不同三点时,对顶角有n对,则m与n的关系是( )
A. m=n B. m>n C. m<n D. m+n=10
解答: 解:因为三条直线两两相交与是否交于同一点无关,所以m=n,故选A.
5.下列图形中∠1与∠2是对顶角的是( )
A. B. C. D.
解答: 解:根据对顶角的定义,两条直线相交后所得的只有一个公共顶点且两个角的两边互为反向延长线,这样的两个角叫做对顶角.符合条件的只有B,
故选B.
6.已知,OA⊥OC,且∠AOB:∠AOC=2:3,则∠BOC的度数为( )
A. 30° B. 150° C. 30°或150° D. 90°
解答: 解:∵OA⊥OC,
∴∠AOC=90°,
∵∠AOB:∠AOC=2:3,
∴∠AOB=60°.
因为∠AOB的位置有两种:一种是在∠AOC内,一种是在∠AOC外.
①当在∠AOC内时,∠BOC=90°﹣60°=30°;
②当在∠AOC外时,∠BOC=90°+60°=150°.
故选C.
7.如图,在△ABC中,AC⊥BC,CD⊥AB,则图中能表示点到直线(或线段)的距离的线段有( ) A. 2条 B. 3条 C. 4条 D. 5条
解答: 解:表示点C到直线AB的距离的线段为CD;
表示点B到直线AC的距离的线段为BC;表示点A到直线BC的距离的线段为AC;
表示点A到直线DC的距离的线段为AD;表示点B到直线DC的距离的线段为BD.
故选D.
8.(1)延长射线OM; (2)平角是一条射线;(3)线段、射线都是直线的一部分;(4)锐角一定小于它的余角;(5)大于直角的角是钝角;(6)一个锐角的补角与这个锐角的余角的差是90°; (7)相等的两个角是对顶角; (8)若∠A+∠B+∠C=180°,则这三个角互补;(9)互为邻补角的两个角的平分线互相垂直.以上说法正确的有( )
A. 2个 B. 3个 C. ?4个 D. ?5个
解答: 解:(1)射线有起点,终点在无穷远处,无法延长,故(1)错误;
(2)角的定义是具有公共点的两条射线组成的图形.故(2)错误;
(3)在直线上画两点,两点之间的部分就是一条线段,在直线上画一点,这点把直线分成两部分,这两部分就是两个相反方向的射线.所以线段和射线都是直线的一部分.故(3)正确;
(4)两个角的和等于90°,就说这两个角互为余角.如45°+45°=90°,故(4)错误;
(5)根据直角的定义可知,大于直角而小于平角的角叫做钝角,故(5)错误;
(6)因为补角=180°﹣这个角,而余角=90°﹣这个角,故(6)项正确;
(7)相等的两个角有很多情况如是两条直线平行时,同位角相等等,故(7)错误;
(8)两个角的和等于180°就说这两个角互为补角,故(8)错误;
(9)根据角平分线的性质,互为邻补角的两个角的平分线互相垂直,故(9)正确.
所以③⑥⑨正确.
故选B.
9.在一个平面内,任意四条直线相交,交点的个数最多有( )
A. 7个 B. 6个 C. 5个 D. 4个
分析: 在平面上画出4条直线,当这4条直线经过同一个点时,有1个交点;当3条直线经过同一个点,第4条不经过该点时,有4个交点;当4条直线不经过同一点时,有6个交点.
解答: 解:如图所示:
①当4条直线经过同一个点时,有1个交点;②当3条直线经过同一个点,第4条不经过该点时,
有4个交点;③当4条直线不经过同一点时,有6个交点.综上所述,4条直线相交最多有6个交点.故选B.
10.下列图形中,线段PQ的长表示点P到直线MN的距离是( )
A. B. C. D.
解答: 解:利用点到直线的距离的定义可知:线段PQ的长表示点P到直线MN的距离的是A图.
故选A.
11.已知线段AB=10cm,点A,B到直线l的距离分别为6cm,4cm.符合条件的直线l有( )
A. 1条 B. 2条 C. 3条 D. 4条
解答: 解:在线段AB的两旁可分别画一条满足条件的直线;作线段AB的垂线,将线段AB分成6cm,4cm两部分,所以符合条件的直线l有3条,故选C.
点评: 此题主要考查了从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离的定义.
12.下面四个图形中,∠1与∠2是对顶角的图形的个数是( )
A. 0 B. 1 C. 2 D. 3
解答: 解:根据对顶角的定义可知:只有图3中的是对顶角,其它都不是.故选B.
二.填空题(共9小题)
13.观察下列图形,并阅读,图形下面的相关字.
两条直线相交最多有1个交点 三条直线相交最多有3个交点 四条直线相交最多有6个交点
则n条直线最多有 个交点.
解答: 解:∵两条直线相交,最多有1个交点,即1=,三条直线两条直线相交,最多有3个交点,即3= 四条直线相交,最多有6个交点,即6=
5条直线相交,最多有10个交点,即5=,∴n条直线相交,最多的交点个数是,故答案为:.
14.如图:A、O、B在同一直线上,AB⊥OE,OC⊥OD,则图中互余的角共有 4 对.
解答: 解:由已知条件得,∠AOE=∠BOE=∠DOC=90°,
∴∠BOD+∠DOE=90°,∠DOE+∠COE=90°,∠COE+∠AOC=90°,∴∠DOE=∠AOC,
∴∠BOD+∠AOC=90°,∴互余的角共有四对.
15.图中有 12 对对顶角.
解答: 解:如图,单个角组成的对顶角有4对,两个角看做一个角组成的对顶角有4对,
三个角看做一个角组成的对顶角有4对,所以对顶角共有4×3=12对.故应填12.
16.公园里准备修6条甬道,并在甬道交叉路口处设一个报亭,这样的报亭最多设 15 个.
分析: 根据6条直线只能与其余5条直线有5个交点,推出共有6×5个交点,但每个交点都重复一次,故共有6×5×=15个交点,即可得出答案.
解答: 解:∵有6条直线,最多与前6﹣1=5条直线有6﹣1=5个交点,
∴最多有6×(6﹣1)÷2=15个交点,
故答案为:15.
17.(2006 南宁)如图,已知AB、CD相交于点O,OE⊥AB,∠EOC=28°,则∠AOD= 62 度.
17题图 18题图 19题图
解:∵OE⊥AB,∠EOC=28°,∴∠COB=90°﹣∠EOC=62°,∴∠AOD=62°(对顶角相等).
18.如图,OA⊥OB,∠BOC=30°,OD平分∠AOC,则∠BOD= 30 度.
解答: 解:OA⊥OB,∠AOB=90°,即∠AOD+BOD=90°;∵OD平分∠AOC,
∴∠AOD=∠DOC,即∠BOD+∠BOC+BOD=90°,即2∠BOD+∠BOC=90°
∵∠BOC=30°,∴∠BOD=30°.故填30.
19.如图,已知直线AB、CD、EF相交于点O,∠1=95°,∠2=32°,则∠BOE= 53 度.
解答: 解:∵∠BOE与∠AOF是对顶角,∴∠BOE=∠AOF,∵∠1=95°,∠2=32°,∠COD是平角,∴∠AOF=180°﹣∠1﹣∠2=180°﹣95°﹣32°=53°,即∠BOE=53°.
20.如图,直线AB,CD相交于点O,∠AOC=54°,∠1比∠2大10°,则∠1= 32 度;∠2= 22 度.
解答: 解:∵∠AOC与∠BOD是对顶角,∴∠1+∠2=∠AOC=54°,∵∠1﹣∠2=10°,
∴∠1=32°,∠2=22°.
20题图 21题图
21.如图,直线AB、CD相交于点O,OE⊥AB,O为垂足,如果∠EOD=38°,则∠AOC= 52 度,∠COB= 128 度.
解答: 解:∵OE⊥AB,∴∠EOB=90°,又∠EOD=38°,∴∠DOB=90°﹣38°=52°,∵∠AOC=∠DOB,∴∠AOC=52°,∵∠COB与∠AOC互补,∴∠COB=180°﹣52°=128°.
三.解答题(共9小题)
22.已知点C在直线a外,点A在直线a上,且AC=2厘米.
(1)设d是点C到直线a的距离,求d的取值范围;
(2)若直线BD垂直于直线a,垂足为B.则直线BD与直线AC有怎样的位置关系,请画示意图表示(每种位置关系画一个示意图).
分析: (1)由于点C在直线a外,所以AC和直线a有两种可能:①垂直相交,此时d=AC;②不垂直相交,此时d<AC.由此即可确定d的取值范围;
(2)如图,有四种位置关系:分别是重合、相交(两种)、平行.
解答: (1)解:∵当AC⊥直线a时,A为垂足,此时d=AC=2厘米,
∴0<d≤2;
(2)解:如图所示:
,
标出AC与BD交于点E.
23.如图所示,OA丄OB,OC丄OD,OE为∠BOD的平分线,∠BOE=22°,求∠AOC的度数.
解答: 解:∵OA丄OB,OC丄OD,∴∠AOB=∠COD=90°,∵OE为∠BOD的平分线,
∴∠BOD=44°,∴∠AOC=360°﹣(∠AOB+∠COD+∠BOD),=360°﹣(90°+90°+44°),=136°.
23题图 24题图 25题图
24.如图,直线BC与MN相交于点O,AO⊥BC,OE平分∠BON,若∠EON=20°,求∠AOM和∠NOC的度数.
解答: 解:∵OE平分∠BON,∴∠BON=2∠EON=2×20°=40°,∴∠NOC=180°﹣∠BON=180°﹣40°=140°,∠MOC=∠BON=40°,∵AO⊥BC,∴∠AOC=90°,∴∠AOM=∠AOC﹣∠MOC=90°﹣40°=50°,所以∠NOC=140°,∠AOM=50°.
25.如图①②所示,将两个相同三角板的两个直角顶点O重合在一起,像图①②那样放置.
(1)若∠BOC=60°,如图①,猜想∠AOD的度数;
(2)若∠BOC=70°,如图②,猜想∠AOD的度数;
(3)猜想∠AOD和∠BOC的关系,并写出理由.
解答: 解:(1)∵∠AOB=90°,∠BOC=60°,∴∠AOC=∠AOB﹣∠BOC=90°﹣60°=30°.
又∵∠COD=90°,∴∠AOD=∠AOC+∠COD=30°+90°=120°.
(2)∵∠AOB+∠COD+∠BOC+∠AOD=360°,∠AOB=90°,∠COD=90°,∠BOC=70°,
∴∠AOD=360°﹣∠AOB﹣∠COD﹣∠BOC=360°﹣90°﹣90°﹣70°=110°.
(3)由(1)知∠AOD+∠BOC=120°+60°=180°,由(2)知∠AOD+∠BOC=110°+70°=180°.
故由(1),(2)可猜想:∠AOD+∠BOC=180°.理由:∵∠AOD=∠AOC+∠COD=∠AOC+90°,∠BOC=∠COD﹣∠BOD=90°﹣∠BOD,∠AOC=∠BOD,∴∠AOD+∠BOC=180°.
26.观察下列各图,寻找对顶角(不含平角):
(1)如图a,图中共有 2 对对顶角;
(2)如图b,图中共有 6 对对顶角;
(3)如图c,图中共有 12 对对顶角;
(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可形成 (n﹣1)n 对对顶角;
(5)若有2008条直线相交于一点,则可形成 4030056 对对顶角.
解答: 解:(1)如图a,图中共有1×2=2对对顶角;
(2)如图b,图中共有2×3=6对对顶角;
(3)如图c,图中共有3×4=12对对顶角;
(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,
若有n条直线相交于一点,则可形成(n﹣1)n对对顶角;
(5)若有2008条直线相交于一点,则可形成(2008﹣1)×2008=4 030 056对对顶角.
27.如图,直线AB、CD相交于O,OD平分∠AOF,OE⊥CD于点O,∠1=50°,求∠COB、∠BOF的度数.
解答: 解:∵OE⊥CD于点O,∠1=50°,∴∠AOD=90°﹣∠1=40°,∵∠BOC与∠AOD是对顶角,∴∠BOC=∠AOD=40°.∵OD平分∠AOF,∴∠DOF=∠AOD=40°,∴∠BOF=180°﹣∠BOC﹣∠DOF=180°﹣40°﹣40°=100°.
27题图 28题图
28.如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD.
(1)图中除直角外,还有相等的角吗?请写出两对:
① ∠COE=∠BOF ;② ∠COP=∠BOP .
(2)如果∠AOD=40°.
①那么根据 对顶角相等 ,可得∠BOC= 40 度.
②因为OP是∠BOC的平分线,所以∠COP=∠ BOC = 20 度.
③求∠BOF的度数.
解答: 解:(1)∠COE=∠BOF、∠COP=∠BOP、∠COB=∠AOD(写出任意两个即可);
(2)①对顶角相等,40度;②∠COP=∠BOC=20°;③∵∠AOD=40°,∴∠BOF=90°﹣40°=50°.
29.如图所示,O是直线AB上一点,∠AOC=∠BOC,OC是∠AOD的平分线.
(1)求∠COD的度数.
(2)判断OD与AB的位置关系,并说出理由.
解答: 解:(1)∵∠AOC+∠BOC=180°,∠AOC=∠BOC,∴∠BOC+∠BOC=180°,
解得∠BOC=135°,∴∠AOC=180°﹣∠BOC=180°﹣135°=45°,∵OC平分∠AOD,∴∠COD=∠AOC=45°.
(2)OD⊥AB.理由:由(1)知∠AOC=∠COD=45°,∴∠AOD=∠AOC+∠COD=90°,
∴OD⊥AB(垂直定义).
30.如图,直线AB、CD相交于O,OE平分∠AOC,∠BOC﹣∠BOD=20°,求∠BOE的度数.
解答: 解:∵∠BOC﹣∠BOD=20°且∠BOC+∠BOD=180°,
∴∠BOC=100°,∠AOC=80°,
∵OE平分∠AOC,
∴∠EOC=∠AOC=40°,
∴∠BOE=∠BOC+∠EOC=140°.
点评: 本题考查邻补角的定义和对顶角的性质以及角平分线的定义,是一个需要熟记的内容.
一.选择题(共12小题)
1.在直线AB上任取一点O,过点O作射线OC,OD,使OC⊥OD,当∠AOC=30°时,∠BOD的度数是( )
A. 60° B. 120° C. 60°或90° D. 60°或120°
2.两条相交直线所成的角中( )
A.必有一个钝角 B. 必有一个锐角
C.必有一个不是钝角 D. 必有两个锐角
3.如图,OA⊥OC,OB⊥OD,4位同学观察图形后分别说了自己的观点.甲:∠AOB=∠COD;乙:∠BOC+∠AOD=180°;丙:∠AOB+∠COD=90°;丁:图中小于平角的角有5个.其中正确的结论是( ) A.1个 B.2个 C. 3个 D.4个
4.三条直线两两相交于同一点时,对顶角有m对;交于不同三点时,对顶角有n对,则m与n的关系是( )
A. m=n B. m>n C. m<n D. m+n=10
5.下列图形中∠1与∠2是对顶角的是( )
A. B. C. D.
6.已知,OA⊥OC,且∠AOB:∠AOC=2:3,则∠BOC的度数为( )
A.30° B. 150° C. 30°或150° D. 90°
7.如图,在△ABC中,AC⊥BC,CD⊥AB,则图中能表示点到直线(或线段)的距离的线段有( )A.2条 B.3条 C.4条 D.5条
8.(1)延长射线OM; (2)平角是一条射线;(3)线段、射线都是直线的一部分;(4)锐角一定小于它的余角;(5)大于直角的角是钝角;(6)一个锐角的补角与这个锐角的余角的差是90°; (7)相等的两个角是对顶角; (8)若∠A+∠B+∠C=180°,则这三个角互补;(9)互为邻补角的两个角的平分线互相垂直.以上说法正确的有( )
A. 2个 B. 3个 C. ?4个 D. ?5个
9.在一个平面内,任意四条直线相交,交点的个数最多有( )
A. 7个 B. 6个 C. 5个 D. 4个
10.下列图形中,线段PQ的长表示点P到直线MN的距离是( )
A. B. C. D.
11.已知线段AB=10cm,点A,B到直线l的距离分别为6cm,4cm.符合条件的直线l有( )
A. 1条 B. 2条 C. 3条 D. 4条
12.下面四个图形中,∠1与∠2是对顶角的图形的个数是( )
A. 0 B. 1 C. 2 D. 3
二.填空题(共9小题)
13.观察下列图形,并阅读,图形下面的相关字.
两条直线相交最多有1个交点 三条直线相交最多有3个交点 四条直线相交最多有6个交点
则n条直线最多有 _________ 个交点.
14.如图:A、O、B在同一直线上,AB⊥OE,OC⊥OD,则图中互余的角共有 ___对.
15.图中有 _________ 对对顶角.
16.公园里准备修6条甬道,并在甬道交叉路口处设一个报亭,这样的报亭最多设 ________个.
17.(2006 南宁)如图,已知AB、CD相交于点O,OE⊥AB,∠EOC=28°,则∠AOD= _________ 度.
18题图 19题图
18.如图,OA⊥OB,∠BOC=30°,OD平分∠AOC,则∠BOD= _________ 度.
19.如图,已知直线AB、CD、EF相交于点O,∠1=95°,∠2=32°,则∠BOE= _________ 度.
20.如图,直线AB,CD相交于点O,∠AOC=54°,∠1比∠2大10°,则∠1= _________ 度;∠2= _________ 度.
21.如图,直线AB、CD相交于点O,OE⊥AB,O为垂足,如果∠EOD=38°,则∠AOC= _________ 度,∠COB= _________ 度.
19题图 20题图 21题图
三.解答题(共9小题)
22.已知点C在直线a外,点A在直线a上,且AC=2厘米.
(1)设d是点C到直线a的距离,求d的取值范围;
(2)若直线BD垂直于直线a,垂足为B.则直线BD与直线AC有怎样的位置关系,请画示意图表示(每种位置关系画一个示意图).
23.如图所示,OA丄OB,OC丄OD,OE为∠BOD的平分线,∠BOE=22°,求∠AOC的度数.
23题图 24题图 25题图
24.如图,直线BC与MN相交于点O,AO⊥BC,OE平分∠BON,若∠EON=20°,求∠AOM和∠NOC的度数.
25.如图①②所示,将两个相同三角板的两个直角顶点O重合在一起,像图①②那样放置.
(1)若∠BOC=60°,如图①,猜想∠AOD的度数;
(2)若∠BOC=70°,如图②,猜想∠AOD的度数;
(3)猜想∠AOD和∠BOC的关系,并写出理由.
26.观察下列各图,寻找对顶角(不含平角):
(1)如图a,图中共有 _________ 对对顶角;(2)如图b,图中共有 _________ 对对顶角;
(3)如图c,图中共有 _________ 对对顶角;(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可形成 _________ 对对顶角;
(5)若有2008条直线相交于一点,则可形成 _________ 对对顶角.
27.如图,直线AB、CD相交于O,OD平分∠AOF,OE⊥CD于点O,∠1=50°,求∠COB、∠BOF的度数.
28.如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD.
(1)图中除直角外,还有相等的角吗?请写出两对:① _________ ;② _________ .
(2)如果∠AOD=40°.①那么根据 _________ ,可得∠BOC= _________ 度.
②因为OP是∠BOC的平分线,所以∠COP=∠ _________ = _________ 度.
③求∠BOF的度数.
28题图 29题图 30题图
29.如图所示,O是直线AB上一点,∠AOC=∠BOC,OC是∠AOD的平分线.
(1)求∠COD的度数.
(2)判断OD与AB的位置关系,并说出理由.
30.如图,直线AB、CD相交于O,OE平分∠AOC,∠BOC﹣∠BOD=20°,求∠BOE的度数.
第五章5.1相交线提高测试卷参考答案与试题解析
一.选择题(共12小题)
1.在直线AB上任取一点O,过点O作射线OC,OD,使OC⊥OD,当∠AOC=30°时,∠BOD的度数是( )
A. 60° B. 120° C. 60°或90° D. 60°或120°
解答: 解:①当OC、OD在AB的一旁时,
∵OC⊥OD,∠COD=90°,∠AOC=30°,
∴∠BOD=180°﹣∠COD﹣∠AOC=60°;
②当OC、OD在AB的两旁时,
∵OC⊥OD,∠AOC=30°,
∴∠AOD=60°,
∴∠BOD=180°﹣∠AOD=120°.
故选D.
2.两条相交直线所成的角中( )
A. 必有一个钝角 B. 必有一个锐角
C. 必有一个不是钝角 D. 必有两个锐角
解答: 解:当两条直线互相垂直时所成的角都是直角,所以A、B、D都不对.
若都是钝角,则圆周角超过360°,
故选C.
3.如图,OA⊥OC,OB⊥OD,4位同学观察图形后分别说了自己的观点.甲:∠AOB=∠COD;乙:∠BOC+∠AOD=180°;丙:∠AOB+∠COD=90°;丁:图中小于平角的角有5个.其中正确的结论是( )
A. 1个 B. 2个 C. 3个 D. 4个
解答: 解:根据同角的余角相等可得,∠AOB=∠COD,而不会得出∠AOB+∠COD=90°,故甲正确,丙错误;
∠BOC+∠AOD=∠BOC+∠AOB+∠BOD=∠AOC+∠BOD=90°+90°=180°,故乙正确;
图中小于平角的角有∠COD,∠BOD,∠AOD,∠BOC,∠AOC,∠AOB六个,故丁错误.
正确的有两个,故选B.
4.三条直线两两相交于同一点时,对顶角有m对;交于不同三点时,对顶角有n对,则m与n的关系是( )
A. m=n B. m>n C. m<n D. m+n=10
解答: 解:因为三条直线两两相交与是否交于同一点无关,所以m=n,故选A.
5.下列图形中∠1与∠2是对顶角的是( )
A. B. C. D.
解答: 解:根据对顶角的定义,两条直线相交后所得的只有一个公共顶点且两个角的两边互为反向延长线,这样的两个角叫做对顶角.符合条件的只有B,
故选B.
6.已知,OA⊥OC,且∠AOB:∠AOC=2:3,则∠BOC的度数为( )
A. 30° B. 150° C. 30°或150° D. 90°
解答: 解:∵OA⊥OC,
∴∠AOC=90°,
∵∠AOB:∠AOC=2:3,
∴∠AOB=60°.
因为∠AOB的位置有两种:一种是在∠AOC内,一种是在∠AOC外.
①当在∠AOC内时,∠BOC=90°﹣60°=30°;
②当在∠AOC外时,∠BOC=90°+60°=150°.
故选C.
7.如图,在△ABC中,AC⊥BC,CD⊥AB,则图中能表示点到直线(或线段)的距离的线段有( ) A. 2条 B. 3条 C. 4条 D. 5条
解答: 解:表示点C到直线AB的距离的线段为CD;
表示点B到直线AC的距离的线段为BC;表示点A到直线BC的距离的线段为AC;
表示点A到直线DC的距离的线段为AD;表示点B到直线DC的距离的线段为BD.
故选D.
8.(1)延长射线OM; (2)平角是一条射线;(3)线段、射线都是直线的一部分;(4)锐角一定小于它的余角;(5)大于直角的角是钝角;(6)一个锐角的补角与这个锐角的余角的差是90°; (7)相等的两个角是对顶角; (8)若∠A+∠B+∠C=180°,则这三个角互补;(9)互为邻补角的两个角的平分线互相垂直.以上说法正确的有( )
A. 2个 B. 3个 C. ?4个 D. ?5个
解答: 解:(1)射线有起点,终点在无穷远处,无法延长,故(1)错误;
(2)角的定义是具有公共点的两条射线组成的图形.故(2)错误;
(3)在直线上画两点,两点之间的部分就是一条线段,在直线上画一点,这点把直线分成两部分,这两部分就是两个相反方向的射线.所以线段和射线都是直线的一部分.故(3)正确;
(4)两个角的和等于90°,就说这两个角互为余角.如45°+45°=90°,故(4)错误;
(5)根据直角的定义可知,大于直角而小于平角的角叫做钝角,故(5)错误;
(6)因为补角=180°﹣这个角,而余角=90°﹣这个角,故(6)项正确;
(7)相等的两个角有很多情况如是两条直线平行时,同位角相等等,故(7)错误;
(8)两个角的和等于180°就说这两个角互为补角,故(8)错误;
(9)根据角平分线的性质,互为邻补角的两个角的平分线互相垂直,故(9)正确.
所以③⑥⑨正确.
故选B.
9.在一个平面内,任意四条直线相交,交点的个数最多有( )
A. 7个 B. 6个 C. 5个 D. 4个
分析: 在平面上画出4条直线,当这4条直线经过同一个点时,有1个交点;当3条直线经过同一个点,第4条不经过该点时,有4个交点;当4条直线不经过同一点时,有6个交点.
解答: 解:如图所示:
①当4条直线经过同一个点时,有1个交点;②当3条直线经过同一个点,第4条不经过该点时,
有4个交点;③当4条直线不经过同一点时,有6个交点.综上所述,4条直线相交最多有6个交点.故选B.
10.下列图形中,线段PQ的长表示点P到直线MN的距离是( )
A. B. C. D.
解答: 解:利用点到直线的距离的定义可知:线段PQ的长表示点P到直线MN的距离的是A图.
故选A.
11.已知线段AB=10cm,点A,B到直线l的距离分别为6cm,4cm.符合条件的直线l有( )
A. 1条 B. 2条 C. 3条 D. 4条
解答: 解:在线段AB的两旁可分别画一条满足条件的直线;作线段AB的垂线,将线段AB分成6cm,4cm两部分,所以符合条件的直线l有3条,故选C.
点评: 此题主要考查了从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离的定义.
12.下面四个图形中,∠1与∠2是对顶角的图形的个数是( )
A. 0 B. 1 C. 2 D. 3
解答: 解:根据对顶角的定义可知:只有图3中的是对顶角,其它都不是.故选B.
二.填空题(共9小题)
13.观察下列图形,并阅读,图形下面的相关字.
两条直线相交最多有1个交点 三条直线相交最多有3个交点 四条直线相交最多有6个交点
则n条直线最多有 个交点.
解答: 解:∵两条直线相交,最多有1个交点,即1=,三条直线两条直线相交,最多有3个交点,即3= 四条直线相交,最多有6个交点,即6=
5条直线相交,最多有10个交点,即5=,∴n条直线相交,最多的交点个数是,故答案为:.
14.如图:A、O、B在同一直线上,AB⊥OE,OC⊥OD,则图中互余的角共有 4 对.
解答: 解:由已知条件得,∠AOE=∠BOE=∠DOC=90°,
∴∠BOD+∠DOE=90°,∠DOE+∠COE=90°,∠COE+∠AOC=90°,∴∠DOE=∠AOC,
∴∠BOD+∠AOC=90°,∴互余的角共有四对.
15.图中有 12 对对顶角.
解答: 解:如图,单个角组成的对顶角有4对,两个角看做一个角组成的对顶角有4对,
三个角看做一个角组成的对顶角有4对,所以对顶角共有4×3=12对.故应填12.
16.公园里准备修6条甬道,并在甬道交叉路口处设一个报亭,这样的报亭最多设 15 个.
分析: 根据6条直线只能与其余5条直线有5个交点,推出共有6×5个交点,但每个交点都重复一次,故共有6×5×=15个交点,即可得出答案.
解答: 解:∵有6条直线,最多与前6﹣1=5条直线有6﹣1=5个交点,
∴最多有6×(6﹣1)÷2=15个交点,
故答案为:15.
17.(2006 南宁)如图,已知AB、CD相交于点O,OE⊥AB,∠EOC=28°,则∠AOD= 62 度.
17题图 18题图 19题图
解:∵OE⊥AB,∠EOC=28°,∴∠COB=90°﹣∠EOC=62°,∴∠AOD=62°(对顶角相等).
18.如图,OA⊥OB,∠BOC=30°,OD平分∠AOC,则∠BOD= 30 度.
解答: 解:OA⊥OB,∠AOB=90°,即∠AOD+BOD=90°;∵OD平分∠AOC,
∴∠AOD=∠DOC,即∠BOD+∠BOC+BOD=90°,即2∠BOD+∠BOC=90°
∵∠BOC=30°,∴∠BOD=30°.故填30.
19.如图,已知直线AB、CD、EF相交于点O,∠1=95°,∠2=32°,则∠BOE= 53 度.
解答: 解:∵∠BOE与∠AOF是对顶角,∴∠BOE=∠AOF,∵∠1=95°,∠2=32°,∠COD是平角,∴∠AOF=180°﹣∠1﹣∠2=180°﹣95°﹣32°=53°,即∠BOE=53°.
20.如图,直线AB,CD相交于点O,∠AOC=54°,∠1比∠2大10°,则∠1= 32 度;∠2= 22 度.
解答: 解:∵∠AOC与∠BOD是对顶角,∴∠1+∠2=∠AOC=54°,∵∠1﹣∠2=10°,
∴∠1=32°,∠2=22°.
20题图 21题图
21.如图,直线AB、CD相交于点O,OE⊥AB,O为垂足,如果∠EOD=38°,则∠AOC= 52 度,∠COB= 128 度.
解答: 解:∵OE⊥AB,∴∠EOB=90°,又∠EOD=38°,∴∠DOB=90°﹣38°=52°,∵∠AOC=∠DOB,∴∠AOC=52°,∵∠COB与∠AOC互补,∴∠COB=180°﹣52°=128°.
三.解答题(共9小题)
22.已知点C在直线a外,点A在直线a上,且AC=2厘米.
(1)设d是点C到直线a的距离,求d的取值范围;
(2)若直线BD垂直于直线a,垂足为B.则直线BD与直线AC有怎样的位置关系,请画示意图表示(每种位置关系画一个示意图).
分析: (1)由于点C在直线a外,所以AC和直线a有两种可能:①垂直相交,此时d=AC;②不垂直相交,此时d<AC.由此即可确定d的取值范围;
(2)如图,有四种位置关系:分别是重合、相交(两种)、平行.
解答: (1)解:∵当AC⊥直线a时,A为垂足,此时d=AC=2厘米,
∴0<d≤2;
(2)解:如图所示:
,
标出AC与BD交于点E.
23.如图所示,OA丄OB,OC丄OD,OE为∠BOD的平分线,∠BOE=22°,求∠AOC的度数.
解答: 解:∵OA丄OB,OC丄OD,∴∠AOB=∠COD=90°,∵OE为∠BOD的平分线,
∴∠BOD=44°,∴∠AOC=360°﹣(∠AOB+∠COD+∠BOD),=360°﹣(90°+90°+44°),=136°.
23题图 24题图 25题图
24.如图,直线BC与MN相交于点O,AO⊥BC,OE平分∠BON,若∠EON=20°,求∠AOM和∠NOC的度数.
解答: 解:∵OE平分∠BON,∴∠BON=2∠EON=2×20°=40°,∴∠NOC=180°﹣∠BON=180°﹣40°=140°,∠MOC=∠BON=40°,∵AO⊥BC,∴∠AOC=90°,∴∠AOM=∠AOC﹣∠MOC=90°﹣40°=50°,所以∠NOC=140°,∠AOM=50°.
25.如图①②所示,将两个相同三角板的两个直角顶点O重合在一起,像图①②那样放置.
(1)若∠BOC=60°,如图①,猜想∠AOD的度数;
(2)若∠BOC=70°,如图②,猜想∠AOD的度数;
(3)猜想∠AOD和∠BOC的关系,并写出理由.
解答: 解:(1)∵∠AOB=90°,∠BOC=60°,∴∠AOC=∠AOB﹣∠BOC=90°﹣60°=30°.
又∵∠COD=90°,∴∠AOD=∠AOC+∠COD=30°+90°=120°.
(2)∵∠AOB+∠COD+∠BOC+∠AOD=360°,∠AOB=90°,∠COD=90°,∠BOC=70°,
∴∠AOD=360°﹣∠AOB﹣∠COD﹣∠BOC=360°﹣90°﹣90°﹣70°=110°.
(3)由(1)知∠AOD+∠BOC=120°+60°=180°,由(2)知∠AOD+∠BOC=110°+70°=180°.
故由(1),(2)可猜想:∠AOD+∠BOC=180°.理由:∵∠AOD=∠AOC+∠COD=∠AOC+90°,∠BOC=∠COD﹣∠BOD=90°﹣∠BOD,∠AOC=∠BOD,∴∠AOD+∠BOC=180°.
26.观察下列各图,寻找对顶角(不含平角):
(1)如图a,图中共有 2 对对顶角;
(2)如图b,图中共有 6 对对顶角;
(3)如图c,图中共有 12 对对顶角;
(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可形成 (n﹣1)n 对对顶角;
(5)若有2008条直线相交于一点,则可形成 4030056 对对顶角.
解答: 解:(1)如图a,图中共有1×2=2对对顶角;
(2)如图b,图中共有2×3=6对对顶角;
(3)如图c,图中共有3×4=12对对顶角;
(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,
若有n条直线相交于一点,则可形成(n﹣1)n对对顶角;
(5)若有2008条直线相交于一点,则可形成(2008﹣1)×2008=4 030 056对对顶角.
27.如图,直线AB、CD相交于O,OD平分∠AOF,OE⊥CD于点O,∠1=50°,求∠COB、∠BOF的度数.
解答: 解:∵OE⊥CD于点O,∠1=50°,∴∠AOD=90°﹣∠1=40°,∵∠BOC与∠AOD是对顶角,∴∠BOC=∠AOD=40°.∵OD平分∠AOF,∴∠DOF=∠AOD=40°,∴∠BOF=180°﹣∠BOC﹣∠DOF=180°﹣40°﹣40°=100°.
27题图 28题图
28.如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD.
(1)图中除直角外,还有相等的角吗?请写出两对:
① ∠COE=∠BOF ;② ∠COP=∠BOP .
(2)如果∠AOD=40°.
①那么根据 对顶角相等 ,可得∠BOC= 40 度.
②因为OP是∠BOC的平分线,所以∠COP=∠ BOC = 20 度.
③求∠BOF的度数.
解答: 解:(1)∠COE=∠BOF、∠COP=∠BOP、∠COB=∠AOD(写出任意两个即可);
(2)①对顶角相等,40度;②∠COP=∠BOC=20°;③∵∠AOD=40°,∴∠BOF=90°﹣40°=50°.
29.如图所示,O是直线AB上一点,∠AOC=∠BOC,OC是∠AOD的平分线.
(1)求∠COD的度数.
(2)判断OD与AB的位置关系,并说出理由.
解答: 解:(1)∵∠AOC+∠BOC=180°,∠AOC=∠BOC,∴∠BOC+∠BOC=180°,
解得∠BOC=135°,∴∠AOC=180°﹣∠BOC=180°﹣135°=45°,∵OC平分∠AOD,∴∠COD=∠AOC=45°.
(2)OD⊥AB.理由:由(1)知∠AOC=∠COD=45°,∴∠AOD=∠AOC+∠COD=90°,
∴OD⊥AB(垂直定义).
30.如图,直线AB、CD相交于O,OE平分∠AOC,∠BOC﹣∠BOD=20°,求∠BOE的度数.
解答: 解:∵∠BOC﹣∠BOD=20°且∠BOC+∠BOD=180°,
∴∠BOC=100°,∠AOC=80°,
∵OE平分∠AOC,
∴∠EOC=∠AOC=40°,
∴∠BOE=∠BOC+∠EOC=140°.
点评: 本题考查邻补角的定义和对顶角的性质以及角平分线的定义,是一个需要熟记的内容.
