2022—2023学年人教版九年级数学上册23.2.3关于原点对称的点的坐标 导学案(含答案)
文档属性
| 名称 | 2022—2023学年人教版九年级数学上册23.2.3关于原点对称的点的坐标 导学案(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 123.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-05 16:25:24 | ||
图片预览

文档简介
23.2.3关于原点对称的点的坐标
【学习目标】
1.理解P与点P′点关于原点对称时,它们的横纵坐标的关系,掌握P(x,y)关于原点的对称点为P′(-x,-y)的运用。
2.复习中心对称以及点关于x轴或y轴对称点的坐标,知识迁移到关于原点对称的点的坐标的关系及其运用。
3.发展空间观念,渗透数形结合思想。
【学习重点】
两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点的对称点P′(-x,-y)及其运用。
【学习难点】
运用中心对称的知识导出关于原点对称的点的坐标的性质及其运用它解决实际问题。
【学习过程】
一、知识回顾。
1.什么叫中心对称和中心对称图形?
2.在下列图形中,是中心对称图形的是( )。
3.下列美丽的图案,既是轴对称图形又是中心对称图形的个数是( )。
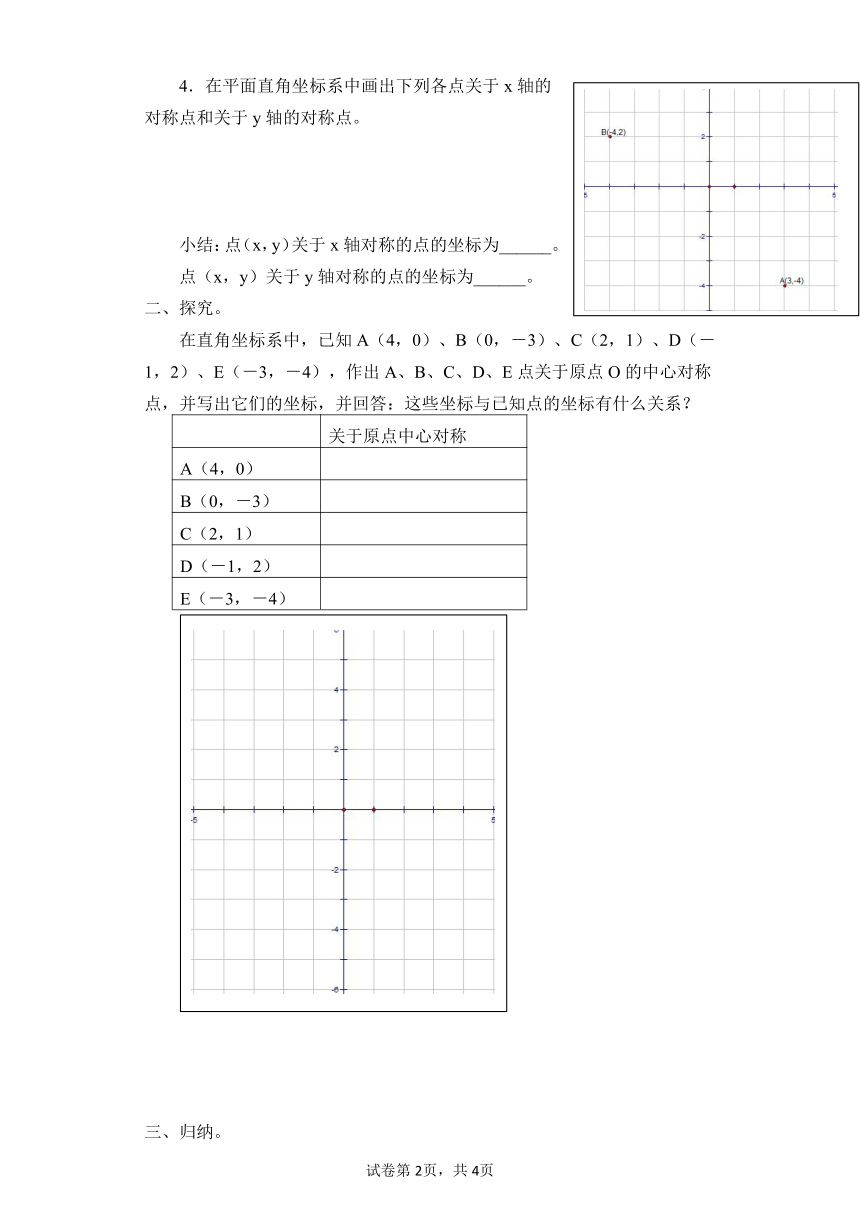
4.在平面直角坐标系中画出下列各点关于x轴的对称点和关于y轴的对称点。
小结:点(x,y)关于x轴对称的点的坐标为______。
点(x,y)关于y轴对称的点的坐标为______。
二、探究。
在直角坐标系中,已知A(4,0)、B(0,-3)、C(2,1)、D(-1,2)、E(-3,-4),作出A、B、C、D、E点关于原点O的中心对称点,并写出它们的坐标,并回答:这些坐标与已知点的坐标有什么关系?
关于原点中心对称
A(4,0)
B(0,-3)
C(2,1)
D(-1,2)
E(-3,-4)
三、归纳。
在平面坐标系中,两个点关于原点对称时,________________。
即:点P(x,y)关于原点O对称,点P'坐标为________________。
引申:若点P与P'的横,纵坐标分别互为相反数,即P(x,y),P'(-x,-y),则点P与P'关于原点O成中心对称。
四、做一做。
如图,利用关于原点对称的点的坐标的特点,作出△ABC关于原点对称的图形。
巩固练习
1.设点A与点B关于x轴对称,点A与点C关于y轴对称,则点B与点C( )
A.关于y轴对称 B.关于x轴对称 C.关于原点对称 D.以上均不对
2.已知点M的坐标是(﹣4,3),则点M关于原点对称的点的坐标是( )
A.(4,3) B.(4,-3) C.(-4,-3) D.(3,-4)
3.已知点A(a,2020)与点B(2021,b)关于x轴对称,则的值为( )
A.-1 B.1 C.2 D.3
4.已知点P的坐标是(﹣6,5),则P点关于原点的对称点的坐标是( )
A.(﹣6,﹣5) B.(6,5) C.(6,﹣5) D.(5,﹣6)
5.已知点P(a+1,)关于原点的对称点在第四象限,则a的取值范围在数轴上表示正确的是( )
A. B.
C. D.
6.直线上有一点,则P点关于原点的对称点为______.
7.若点A(m,5)与点B(-4,n)关于原点成中心对称,则m+n=________.
8.已知点与关于原点对称,则=____________.
9.如图,在直角坐标平面内,已知点A的坐标(﹣2,0).
(1)写出点的坐标;
(2)点B关于原点对称的点C的坐标是 ;点A关于y轴对称的点D的坐标是 ;
(3)四边形ABDC的面积是 ;
(4)在y轴上找一点F,使S△ADF=S△ABD,那么点F的坐标是 .
试卷第1页,共3页
试卷第1页,共3页
参考答案:
C2.B3.B4.C5.C
8.-8
9.(1)(﹣3,4)(2)(3,﹣4),(2,0);(3)16;(4)(0,2)或(0,﹣2)
3 / 3
【学习目标】
1.理解P与点P′点关于原点对称时,它们的横纵坐标的关系,掌握P(x,y)关于原点的对称点为P′(-x,-y)的运用。
2.复习中心对称以及点关于x轴或y轴对称点的坐标,知识迁移到关于原点对称的点的坐标的关系及其运用。
3.发展空间观念,渗透数形结合思想。
【学习重点】
两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点的对称点P′(-x,-y)及其运用。
【学习难点】
运用中心对称的知识导出关于原点对称的点的坐标的性质及其运用它解决实际问题。
【学习过程】
一、知识回顾。
1.什么叫中心对称和中心对称图形?
2.在下列图形中,是中心对称图形的是( )。
3.下列美丽的图案,既是轴对称图形又是中心对称图形的个数是( )。
4.在平面直角坐标系中画出下列各点关于x轴的对称点和关于y轴的对称点。
小结:点(x,y)关于x轴对称的点的坐标为______。
点(x,y)关于y轴对称的点的坐标为______。
二、探究。
在直角坐标系中,已知A(4,0)、B(0,-3)、C(2,1)、D(-1,2)、E(-3,-4),作出A、B、C、D、E点关于原点O的中心对称点,并写出它们的坐标,并回答:这些坐标与已知点的坐标有什么关系?
关于原点中心对称
A(4,0)
B(0,-3)
C(2,1)
D(-1,2)
E(-3,-4)
三、归纳。
在平面坐标系中,两个点关于原点对称时,________________。
即:点P(x,y)关于原点O对称,点P'坐标为________________。
引申:若点P与P'的横,纵坐标分别互为相反数,即P(x,y),P'(-x,-y),则点P与P'关于原点O成中心对称。
四、做一做。
如图,利用关于原点对称的点的坐标的特点,作出△ABC关于原点对称的图形。
巩固练习
1.设点A与点B关于x轴对称,点A与点C关于y轴对称,则点B与点C( )
A.关于y轴对称 B.关于x轴对称 C.关于原点对称 D.以上均不对
2.已知点M的坐标是(﹣4,3),则点M关于原点对称的点的坐标是( )
A.(4,3) B.(4,-3) C.(-4,-3) D.(3,-4)
3.已知点A(a,2020)与点B(2021,b)关于x轴对称,则的值为( )
A.-1 B.1 C.2 D.3
4.已知点P的坐标是(﹣6,5),则P点关于原点的对称点的坐标是( )
A.(﹣6,﹣5) B.(6,5) C.(6,﹣5) D.(5,﹣6)
5.已知点P(a+1,)关于原点的对称点在第四象限,则a的取值范围在数轴上表示正确的是( )
A. B.
C. D.
6.直线上有一点,则P点关于原点的对称点为______.
7.若点A(m,5)与点B(-4,n)关于原点成中心对称,则m+n=________.
8.已知点与关于原点对称,则=____________.
9.如图,在直角坐标平面内,已知点A的坐标(﹣2,0).
(1)写出点的坐标;
(2)点B关于原点对称的点C的坐标是 ;点A关于y轴对称的点D的坐标是 ;
(3)四边形ABDC的面积是 ;
(4)在y轴上找一点F,使S△ADF=S△ABD,那么点F的坐标是 .
试卷第1页,共3页
试卷第1页,共3页
参考答案:
C2.B3.B4.C5.C
8.-8
9.(1)(﹣3,4)(2)(3,﹣4),(2,0);(3)16;(4)(0,2)或(0,﹣2)
3 / 3
同课章节目录
