九年级上册沪科版课件23.1比例线段(二)课件
文档属性
| 名称 | 九年级上册沪科版课件23.1比例线段(二)课件 |  | |
| 格式 | zip | ||
| 文件大小 | 195.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-03 21:38:22 | ||
图片预览








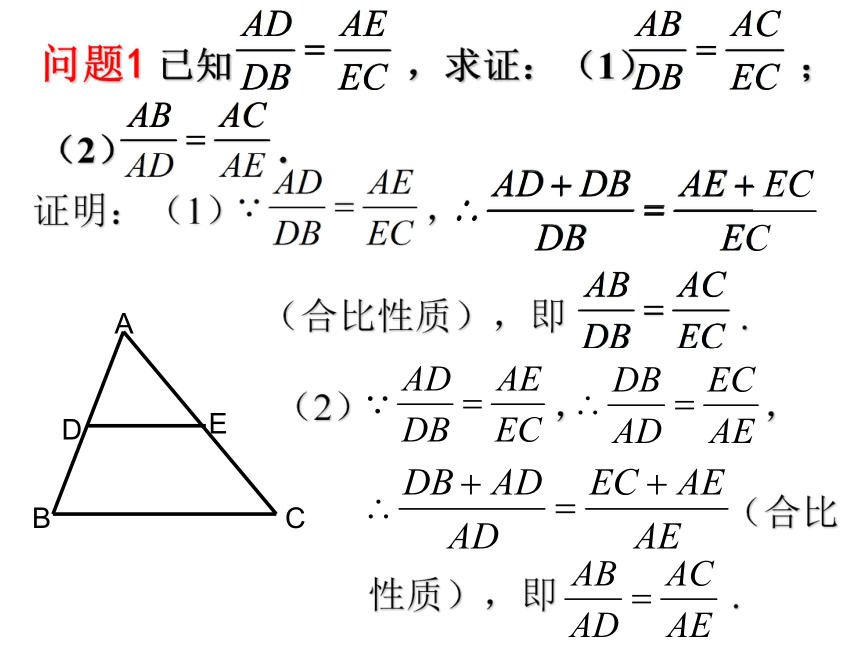
文档简介
课件26张PPT。 第23章 相似形 23.1比例线段(二)比例线段 画两个矩形ABCD和A′ B ′ C ′D ′,使它们的长分别为4.5cm 和 1.5cm,宽分别为2.4cm和0.8cm,并计算线段AB和BC的比,线段A′B ′ 和B ′C ′的比.结论: 在四条线段 a、b、c、d 中,如果 a 和 b 的比等于 c 和 d 的比,那么这四条线段a、b、c、d 叫做成比例的线段,简称比例线段.a :b = c :d.a、b、c 的第四比例项(1)比例的基本性质:反之也成立如果 a:b = b:c ,那么b2=ac
b叫做a、c的比例中项反之如果b2=ac,那么a:b = b:c
b叫做a、c的比例中项例: 从ad = bc 还可以得到那些比例? 解:∵ ad = bc ,两边同除以 ac 得:即 d : c = b : a ;∵ ad = bc ,两边同除以 db 得:即 a : b = c : d ;∵ ad = bc ,两边同除以 dc 得:即 a : c = b : d ;∵ ad = bc ,两边同除以 ab 得:即 d : b = c : a ;(比例的基本性质)在等式两边同加上1, .(2)比例合比性质:如果那么(3)等比性质如果 那么(b+d+…+n≠0),证明:设=k,则a=bk,c=dk,…m=nk,=ka c
b d =m
n = …= a+c+…+m
b+d+…+n= .a
b分母之和不为零,?1.判断下列线段a、b、c、d是否是成比例线段: 例题解析(1)a=4,b=6,c=5,d=10;解 (1) ∵ ∴ 线段a、b、c、d不是成比例线段.∴ 线段a、b、c、d是成比例线段.
2.A、B两地的实际距离AB=250m,画在图上的距离A/B/=5cm,求图上的距离与实际距离的比。
解:取米作为共同的单位长度。AB=250m,
A/B/=0.05m,所以:
练习:⑴若m 是2、3、8 的第四比例项,m= ;⑵若x 是3和27的比例中项,则 x = ;⑶若 a :b :c = 2 : 3 :7 ,又 a + b + c = 36,
则 a = ,b = ,c = . 1296921课堂练习7.已知a、b、c为非0的整数,,求k的值 8.达标练习
3.已知,求的值
,求,的值。4.已知5.已知 = =2,求
6.已知 ==3,求(b+d+f≠0),1.解: 由比例的基本性质得
a2 = (1+a)(1-a)2a2 = 1 X=达标试题2.解:设
则
∴ 已知 ,b+d+f=4,
求a+c+e。3.解:∵即 ∴a+c+e = 4×3 = 12如图,已知 ,由等比性质得 求△ABC与△ADE的周长比。5.解: ∵∴比例线段的概念a :b = c :d.a、b、c 的第四比例项a :b = b :c 在四条线段 a、b、c、d 中,如果 a 和 b 的比等于 c 和 d 的比,那么这四条线段a、b、c、d 叫做成比例的线段,简称比例线段.小结比例的性质1、比例的基本性质:如果 a :b = c :d ,那么 ad = bc.如果 ad = bc,那么 a :b = c :d 2、合比性质:3、等比性质:
b叫做a、c的比例中项反之如果b2=ac,那么a:b = b:c
b叫做a、c的比例中项例: 从ad = bc 还可以得到那些比例? 解:∵ ad = bc ,两边同除以 ac 得:即 d : c = b : a ;∵ ad = bc ,两边同除以 db 得:即 a : b = c : d ;∵ ad = bc ,两边同除以 dc 得:即 a : c = b : d ;∵ ad = bc ,两边同除以 ab 得:即 d : b = c : a ;(比例的基本性质)在等式两边同加上1, .(2)比例合比性质:如果那么(3)等比性质如果 那么(b+d+…+n≠0),证明:设=k,则a=bk,c=dk,…m=nk,=ka c
b d =m
n = …= a+c+…+m
b+d+…+n= .a
b分母之和不为零,?1.判断下列线段a、b、c、d是否是成比例线段: 例题解析(1)a=4,b=6,c=5,d=10;解 (1) ∵ ∴ 线段a、b、c、d不是成比例线段.∴ 线段a、b、c、d是成比例线段.
2.A、B两地的实际距离AB=250m,画在图上的距离A/B/=5cm,求图上的距离与实际距离的比。
解:取米作为共同的单位长度。AB=250m,
A/B/=0.05m,所以:
练习:⑴若m 是2、3、8 的第四比例项,m= ;⑵若x 是3和27的比例中项,则 x = ;⑶若 a :b :c = 2 : 3 :7 ,又 a + b + c = 36,
则 a = ,b = ,c = . 1296921课堂练习7.已知a、b、c为非0的整数,,求k的值 8.达标练习
3.已知,求的值
,求,的值。4.已知5.已知 = =2,求
6.已知 ==3,求(b+d+f≠0),1.解: 由比例的基本性质得
a2 = (1+a)(1-a)2a2 = 1 X=达标试题2.解:设
则
∴ 已知 ,b+d+f=4,
求a+c+e。3.解:∵即 ∴a+c+e = 4×3 = 12如图,已知 ,由等比性质得 求△ABC与△ADE的周长比。5.解: ∵∴比例线段的概念a :b = c :d.a、b、c 的第四比例项a :b = b :c 在四条线段 a、b、c、d 中,如果 a 和 b 的比等于 c 和 d 的比,那么这四条线段a、b、c、d 叫做成比例的线段,简称比例线段.小结比例的性质1、比例的基本性质:如果 a :b = c :d ,那么 ad = bc.如果 ad = bc,那么 a :b = c :d 2、合比性质:3、等比性质:
