23.1《三角形一边的平行线》ppt课件
文档属性
| 名称 | 23.1《三角形一边的平行线》ppt课件 |  | |
| 格式 | zip | ||
| 文件大小 | 97.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-03 21:42:46 | ||
图片预览



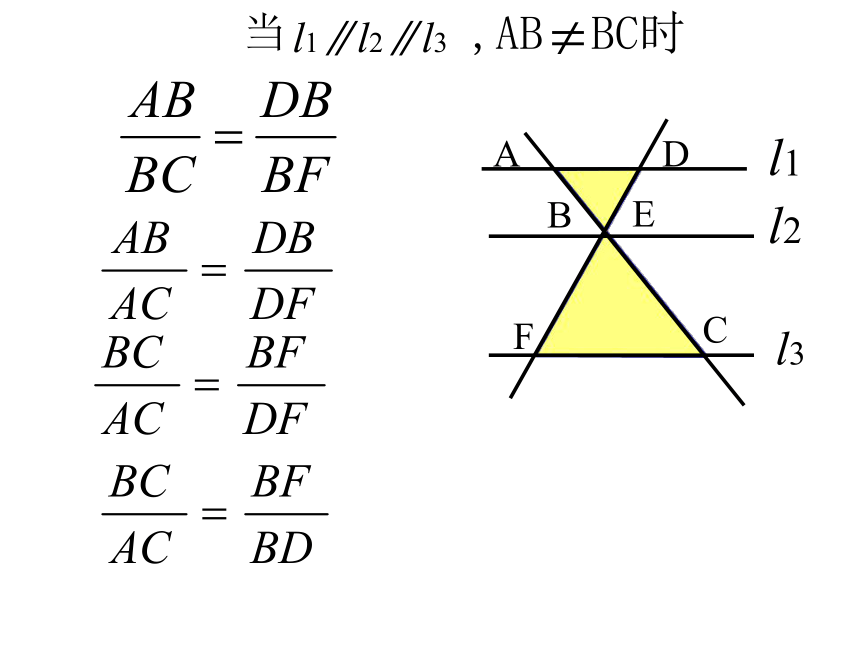
文档简介
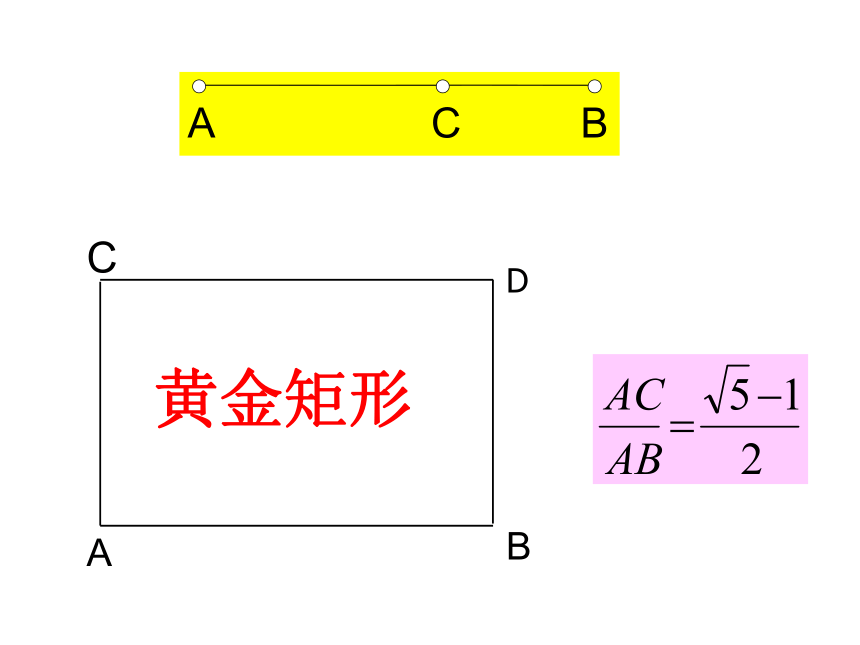
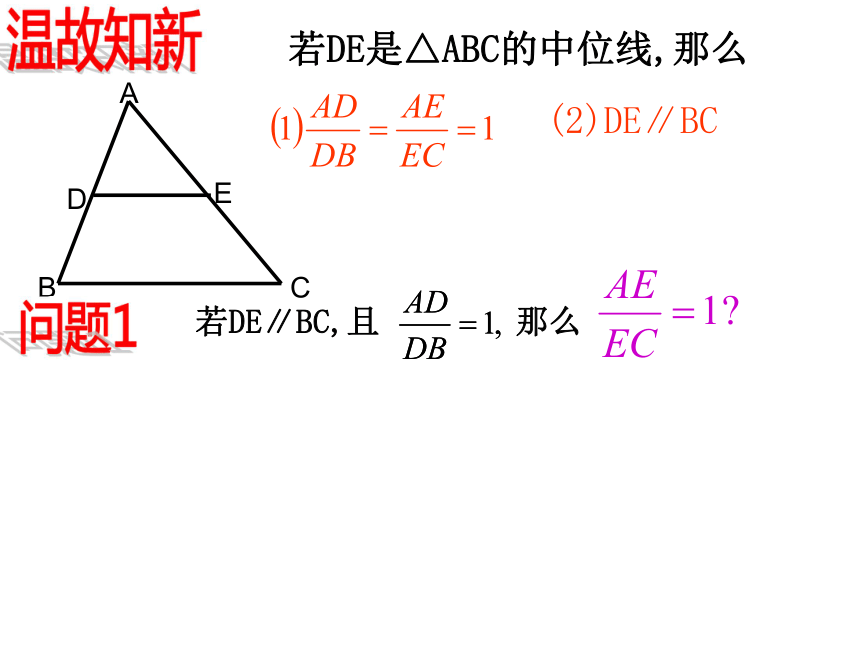
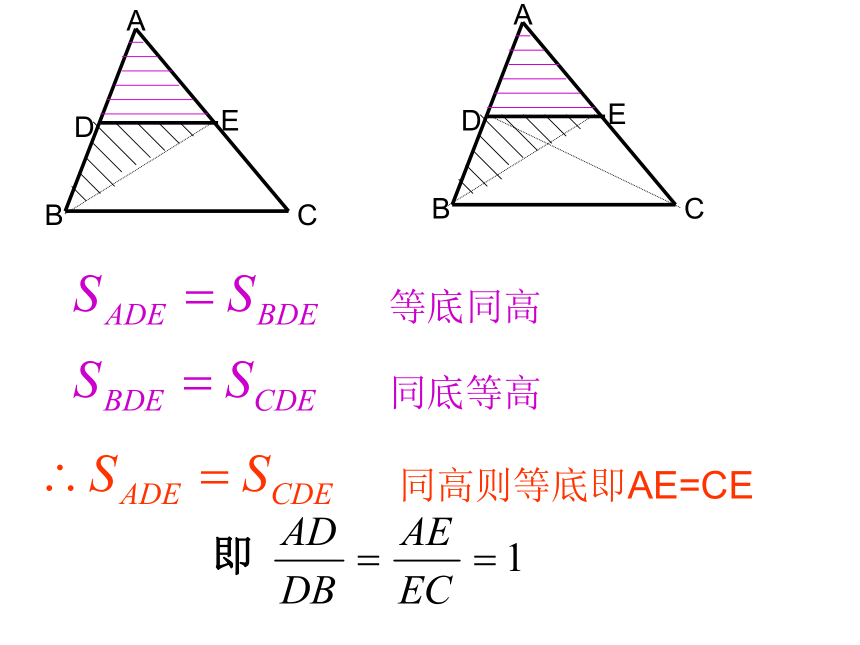
课件34张PPT。 三角形一边的平行线23.1 比例线段(四)a:b=c:d ad=bc 。a:b=b:c b2=ac 。比例的基本性质合比性质如果 ,那么 。如果 ( ),等比性质那么相似形:对应角相等;对应边成比例ABC黄金矩形D温故知新若DE是△ABC的中位线,那么(2)DE∥BC问题1若DE∥BC,且 那么等底同高同底等高同高则等底即AE=CE 即变式1:若将DE 保持与BC平行而进行移
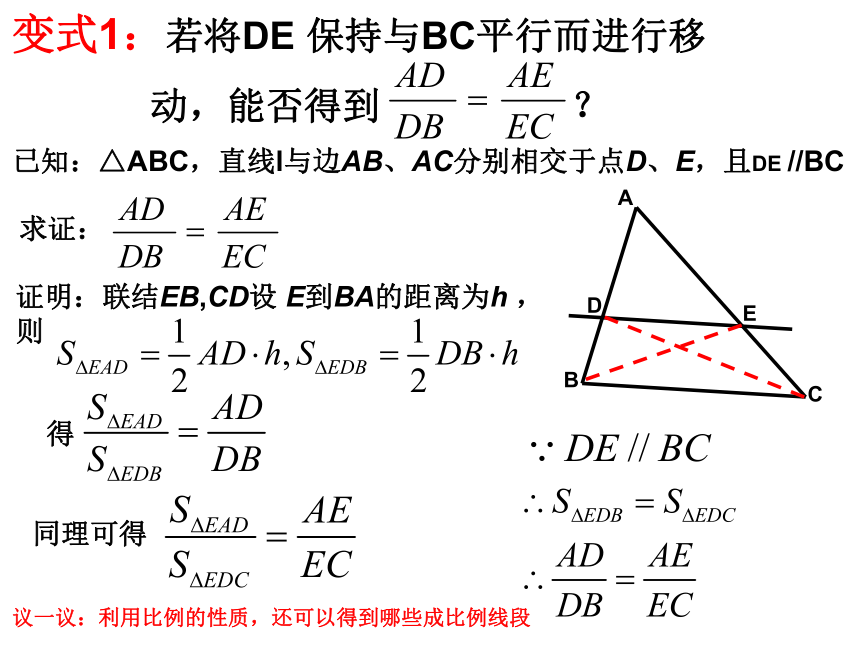
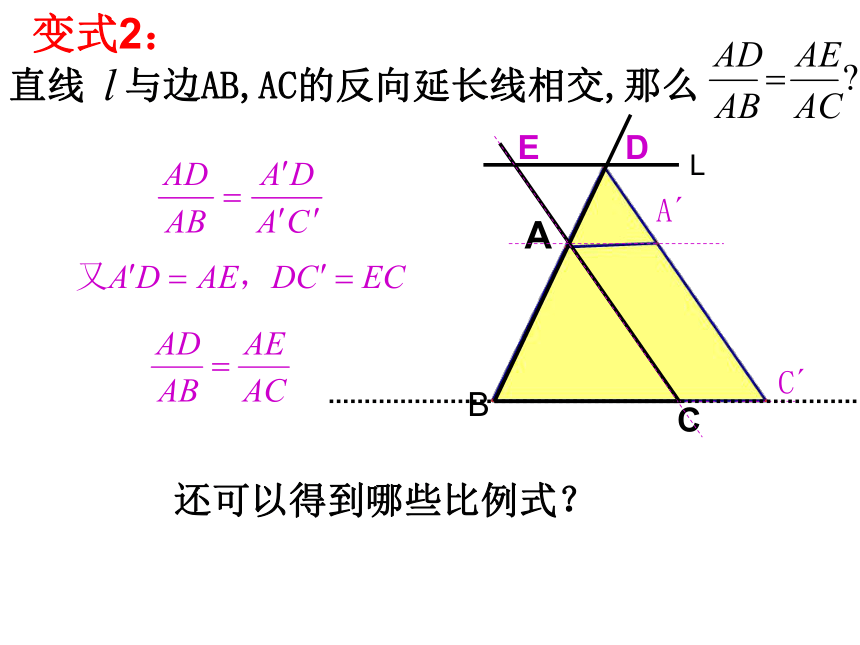
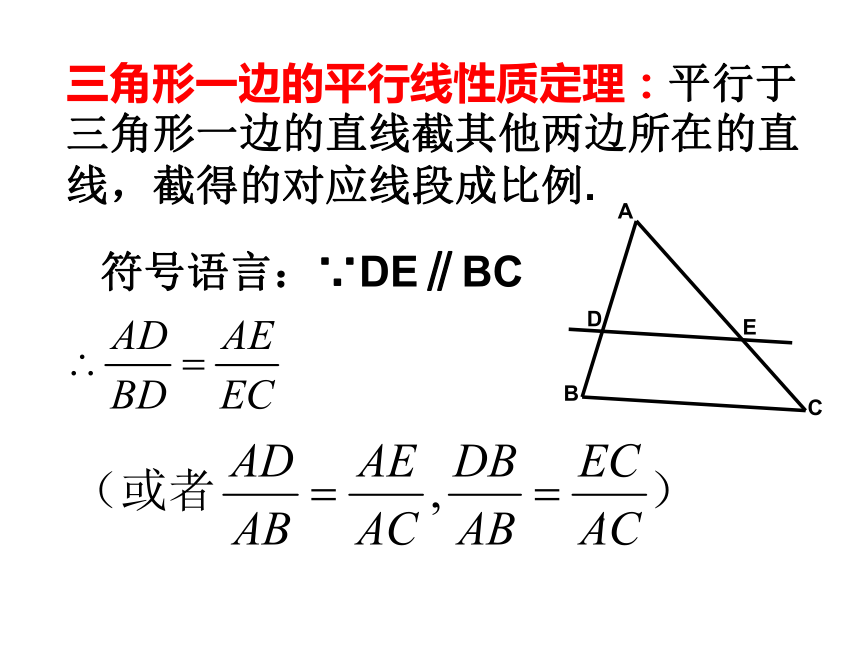
动,能否得到 ? 证明:联结EB,CD设 E到BA的距离为h ,则得同理可得 议一议:利用比例的性质,还可以得到哪些成比例线段 今后常用的有三个比例式:ABCDEL直线 与边AB,AC的反向延长线相交,那么 C′ A′还可以得到哪些比例式?变式2:ABCl1l2 l3DEF,三角形一边的平行线性质定理:平行于三角形一边的直线截其他两边所在的直线,截得的对应线段成比例.符号语言:∵DE∥BC
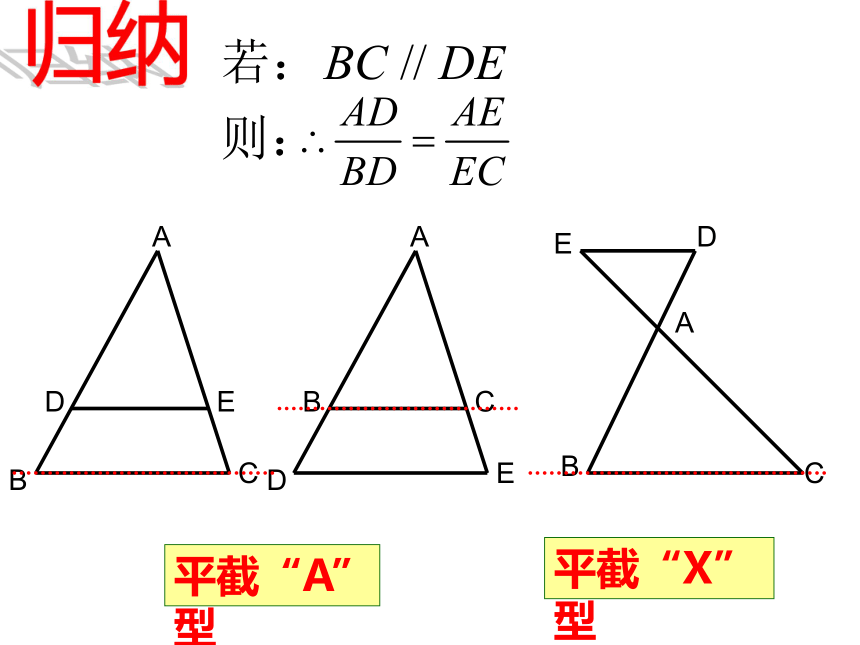
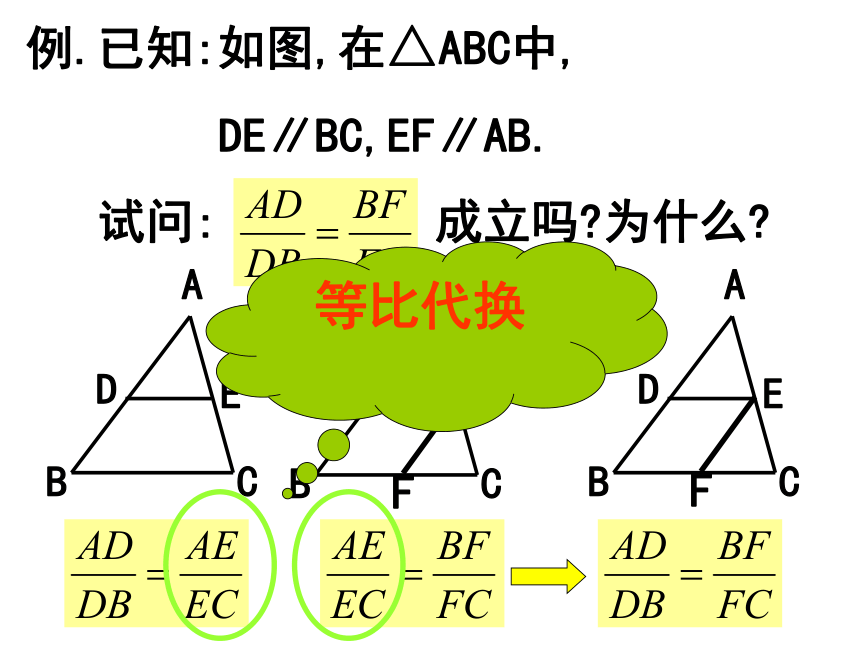
归纳平截“A”型平截“X”型例.已知:如图,在△ABC中,
DE∥BC,EF∥AB.
试问: 成立吗?为什么?F等比代换例.已知:如图,在△ABC中,
DE∥BC,EF∥AB.
试问: 成立吗?F等线代换练习:判断下列比例式是否正确?DE∥BC,EF∥AB.(1)(2)(3)××√例:已知DE∥BC,AB=15,AC=10,BD=6.
求CE.解∵DE∥BC,由AB=15,AC=10,BD=6,得∴CE=4. 1、如图1,DE∥BC,下列比例式中,不成立的是( )A.B.C.D.2、如图2,AB∥CD,AD和BC相交于点O,下列比例式中,正确的是( )A.B.C.D.BD练习ABCl1l2 l3DEF平行线分线段成比例定理:当AB BC时l1∥l2∥l3, 两条直线被三条平行线所截,截得的对应线段成比例.思考:你怎样理解“对应线段成比例”)))ABCl1l2 l3DEF)))))ABCl1l2 l3DEF))))ABCl1l2 l3DEF))))ABCl1l2 l3DEF结论是对应线段成比例.ABCl1l2 l3DEF))))ABCl1l2 l3DEF))))ABCl1l2 l3DEF))))ABCl1l2 l3DEF))))综合以上,结论是对应线段成比例.例:已知线段a,b,c.求作线段x,使a∶b=c∶xx作法略 如果一组平行线在一条直线上截得的线段相等,那么在其它直线上截得的线段也相等.例如:当 l1∥l2∥ l3 , AB=BC 时, 则有 DE=EF.推论:例:已知:线段AB。
求作:线段AB的五等分点。作法:1、作射线AC;2、在射线AC上以任意长顺次截取AD=DE=EF=FG=GH;3、连结HB;4、过点G、F、E、D分别作HB的平行线GL、FK、EJ、DI,分别交AB于L、K、J、I;I、J、K、L就是所求的五等分点;AF交BE于O,且AO=OD=DF,厘米.若BE=60厘米,那么BO=CDEFO201、已知AB∥CD∥EF,AB巩固提高:且AE=BE,那么DF=.CF2、已知AD∥EF∥BC,EFBCADE是AB的中点,则DG=,H是EFBCADGH的中点,.F是的中点BGACCD3、已知AD∥EF∥BC,4、已知△ABC中,AB=AC,AD⊥BC,M是AD的中点,CM交AB于P,DN∥CM交AB于N,如果AB=6厘米,则PN=厘米.2ABCD.MPN∟5、已知△ABC中,CD平分∠ACB,ABCDAE⊥CD交BC于E,EDF∥CB交AB于F,FAF=4厘米,则AB=厘米.8∟
动,能否得到 ? 证明:联结EB,CD设 E到BA的距离为h ,则得同理可得 议一议:利用比例的性质,还可以得到哪些成比例线段 今后常用的有三个比例式:ABCDEL直线 与边AB,AC的反向延长线相交,那么 C′ A′还可以得到哪些比例式?变式2:ABCl1l2 l3DEF,三角形一边的平行线性质定理:平行于三角形一边的直线截其他两边所在的直线,截得的对应线段成比例.符号语言:∵DE∥BC
归纳平截“A”型平截“X”型例.已知:如图,在△ABC中,
DE∥BC,EF∥AB.
试问: 成立吗?为什么?F等比代换例.已知:如图,在△ABC中,
DE∥BC,EF∥AB.
试问: 成立吗?F等线代换练习:判断下列比例式是否正确?DE∥BC,EF∥AB.(1)(2)(3)××√例:已知DE∥BC,AB=15,AC=10,BD=6.
求CE.解∵DE∥BC,由AB=15,AC=10,BD=6,得∴CE=4. 1、如图1,DE∥BC,下列比例式中,不成立的是( )A.B.C.D.2、如图2,AB∥CD,AD和BC相交于点O,下列比例式中,正确的是( )A.B.C.D.BD练习ABCl1l2 l3DEF平行线分线段成比例定理:当AB BC时l1∥l2∥l3, 两条直线被三条平行线所截,截得的对应线段成比例.思考:你怎样理解“对应线段成比例”)))ABCl1l2 l3DEF)))))ABCl1l2 l3DEF))))ABCl1l2 l3DEF))))ABCl1l2 l3DEF结论是对应线段成比例.ABCl1l2 l3DEF))))ABCl1l2 l3DEF))))ABCl1l2 l3DEF))))ABCl1l2 l3DEF))))综合以上,结论是对应线段成比例.例:已知线段a,b,c.求作线段x,使a∶b=c∶xx作法略 如果一组平行线在一条直线上截得的线段相等,那么在其它直线上截得的线段也相等.例如:当 l1∥l2∥ l3 , AB=BC 时, 则有 DE=EF.推论:例:已知:线段AB。
求作:线段AB的五等分点。作法:1、作射线AC;2、在射线AC上以任意长顺次截取AD=DE=EF=FG=GH;3、连结HB;4、过点G、F、E、D分别作HB的平行线GL、FK、EJ、DI,分别交AB于L、K、J、I;I、J、K、L就是所求的五等分点;AF交BE于O,且AO=OD=DF,厘米.若BE=60厘米,那么BO=CDEFO201、已知AB∥CD∥EF,AB巩固提高:且AE=BE,那么DF=.CF2、已知AD∥EF∥BC,EFBCADE是AB的中点,则DG=,H是EFBCADGH的中点,.F是的中点BGACCD3、已知AD∥EF∥BC,4、已知△ABC中,AB=AC,AD⊥BC,M是AD的中点,CM交AB于P,DN∥CM交AB于N,如果AB=6厘米,则PN=厘米.2ABCD.MPN∟5、已知△ABC中,CD平分∠ACB,ABCDAE⊥CD交BC于E,EDF∥CB交AB于F,FAF=4厘米,则AB=厘米.8∟
