23.2《相似三角形的判定预备定理》课件.
文档属性
| 名称 | 23.2《相似三角形的判定预备定理》课件. |  | |
| 格式 | zip | ||
| 文件大小 | 141.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-03 21:48:23 | ||
图片预览


文档简介
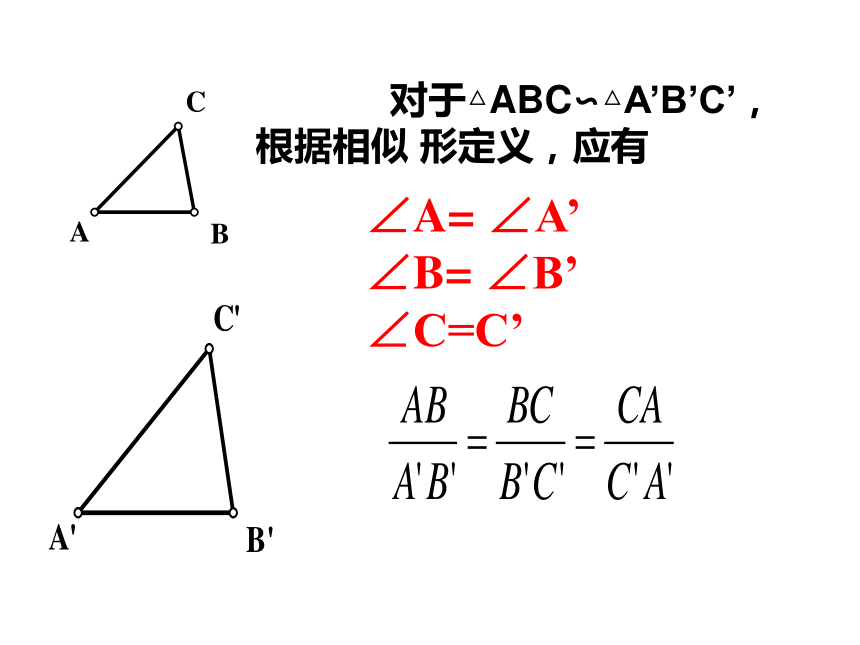
课件21张PPT。相似三角形的判定预备定理 △ABC∽△A/B/C/ 定义:如果两个三角形的对应角相等,对应边成比例,那么这两个三角形叫做相似三角形。表示方法:用“∽”表示 在写两个三角形相似时通常把表示对应顶点的字母写在对应的位置上。 用“∽”表示 ,如:△ABC∽△A/B/C/ 注意 对于△ABC∽△A’B’C’,
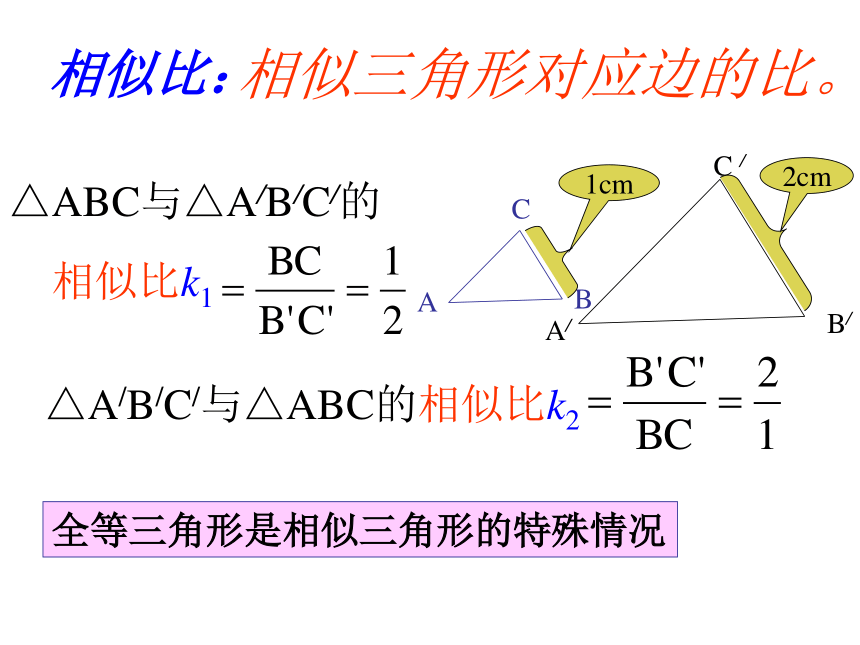
根据相似 形定义,应有相似比:相似三角形对应边的比。全等三角形是相似三角形的特殊情况△ABC与△A/B/C/的
相似比k1△A/B/C/与△ABC的相似比k2它们是相似三角形吗?为什么?课前复习:1、两个全等三角形一定相似吗?为什么?2、两个直角三角形一定相似吗?为什么?
两个等腰直角三角形呢?3、两个等腰三角形一定相似吗?为什么?
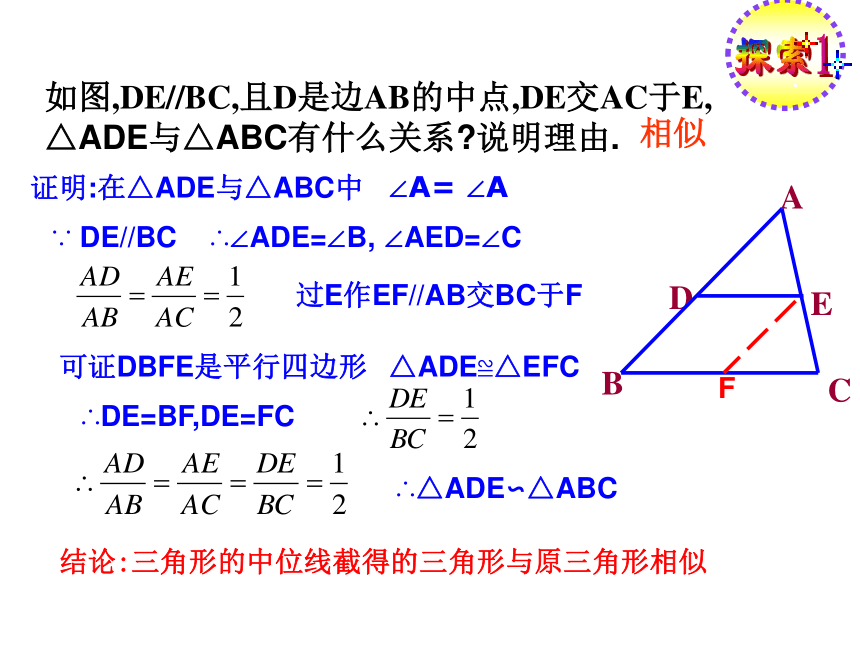
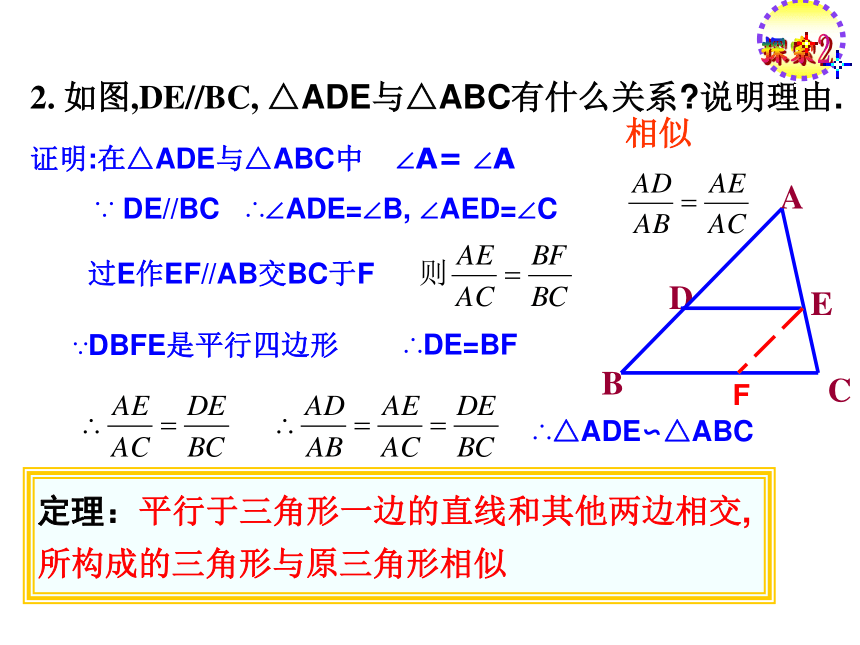
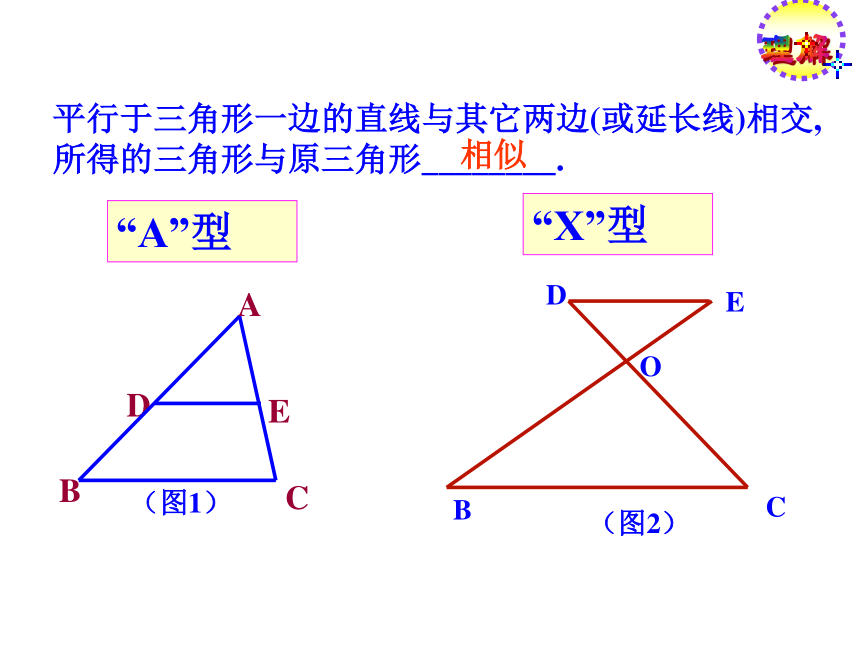
两个等边三角形呢?相似比是多少?巩固练习:如图,DE//BC,且D是边AB的中点,DE交AC于E, △ADE与△ABC有什么关系?说明理由.相似证明:在△ADE与△ABC中∠A= ∠A∵ DE//BC∴∠ADE=∠B, ∠AED=∠C过E作EF//AB交BC于F可证DBFE是平行四边形F△ADE≌△EFC∴DE=BF,DE=FC∴△ADE∽△ABC结论:三角形的中位线截得的三角形与原三角形相似探索12. 如图,DE//BC, △ADE与△ABC有什么关系?说明理由.相似ABCDE证明:在△ADE与△ABC中∠A= ∠A∵ DE//BC∴∠ADE=∠B, ∠AED=∠C过E作EF//AB交BC于F∵DBFE是平行四边形F∴DE=BF定理:平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似∴△ADE∽△ABC探索2平行于三角形一边的直线与其它两边(或延长线)相交,所得的三角形与原三角形________.相似“A”型 “X”型 理解巩固练习 如图,在平行四边形ABCD中,E是AB上的一点, CE和DA的延长线交于点F根据本节所得预备定理找出图中相似三角形(全等三角形除外). ABCDEF 如图,在平行四边形ABCD中,E是AB上的一点, CE和DA的延长线交于点F根据本节所得预备定理找出图中相似三角形(全等三角形除外).巩固练习 ABCDEF 如图,在平行四边形ABCD中,E是AB上的一点, CE和DA的延长线交于点F根据本节所得预备定理找出图中相似三角形(全等三角形除外).巩固练习 如图,在平行四边形ABCD中,E是AB上的一点, CE和DA的延长线交于点F根据本节所得预备定理找出图中相似三角形(全等三角形除外).变式一:连接BD巩固练习 如图,在平行四边形ABCD中,E是AB上的一点, CE和DA的延长线交于点F根据本节所得预备定理找出图中相似三角形(全等三角形除外).变式二:G为BC延长线上一点G巩固练习 1.已知:如图,AB∥EF ∥CD,3图中共有____对相似三角形。 △EOF∽△COD AB∥EF △AOB∽ △FOE AB∥CDEF∥CD△AOB ∽△DOC理解请写出它们的对应边的比例式理解 1.如图,△ABC 中,DE∥BC,GF∥AB,DE、GF交于点O,则图中与△ABC相似的三角形共有多少个?请你写出来.解: 与△ABC相似的三角形有3个: △ADE
△GFC
△GOE运用2.如图,已知DE ∥ BC,AE=50cm,EC=30cm,BC=70cm,
∠BAC=450,∠ACB=400.
(1)求∠AED和∠ADE的大小;(2)求DE的长.
(2)解: (1)DE ∥ BC△ADE∽△ABC∠AED=∠C=400.△ADE∽△ABC运用在△ADE中, ∠ADE=1800-400-450=950.3.如图,在△ABC中,DG∥EH∥FI∥BC,
(1)请找出图中所有的相似三角形;
(2)如果AD=1,DB=3,那么DG:BC=_____。△ADG∽△AEH∽△AFI∽△ABC1:4运用4.有一块呈三角形形状的草坪,其中一边的长是20m,在这个草坪的图纸上,这条边长5cm,其他两边的长都是3.5cm,求该草坪其他两边的实际长度。思考下列问题:1、草坪的形状与其图纸上相应的形状是否相似? 2.它们的相似比是多少?解:设其他两边的实际长度都是xcm,则
X=3.5×400=1400cm=14m
答:草坪其他两边的实际长度都是14m运用小结
根据相似 形定义,应有相似比:相似三角形对应边的比。全等三角形是相似三角形的特殊情况△ABC与△A/B/C/的
相似比k1△A/B/C/与△ABC的相似比k2它们是相似三角形吗?为什么?课前复习:1、两个全等三角形一定相似吗?为什么?2、两个直角三角形一定相似吗?为什么?
两个等腰直角三角形呢?3、两个等腰三角形一定相似吗?为什么?
两个等边三角形呢?相似比是多少?巩固练习:如图,DE//BC,且D是边AB的中点,DE交AC于E, △ADE与△ABC有什么关系?说明理由.相似证明:在△ADE与△ABC中∠A= ∠A∵ DE//BC∴∠ADE=∠B, ∠AED=∠C过E作EF//AB交BC于F可证DBFE是平行四边形F△ADE≌△EFC∴DE=BF,DE=FC∴△ADE∽△ABC结论:三角形的中位线截得的三角形与原三角形相似探索12. 如图,DE//BC, △ADE与△ABC有什么关系?说明理由.相似ABCDE证明:在△ADE与△ABC中∠A= ∠A∵ DE//BC∴∠ADE=∠B, ∠AED=∠C过E作EF//AB交BC于F∵DBFE是平行四边形F∴DE=BF定理:平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似∴△ADE∽△ABC探索2平行于三角形一边的直线与其它两边(或延长线)相交,所得的三角形与原三角形________.相似“A”型 “X”型 理解巩固练习 如图,在平行四边形ABCD中,E是AB上的一点, CE和DA的延长线交于点F根据本节所得预备定理找出图中相似三角形(全等三角形除外). ABCDEF 如图,在平行四边形ABCD中,E是AB上的一点, CE和DA的延长线交于点F根据本节所得预备定理找出图中相似三角形(全等三角形除外).巩固练习 ABCDEF 如图,在平行四边形ABCD中,E是AB上的一点, CE和DA的延长线交于点F根据本节所得预备定理找出图中相似三角形(全等三角形除外).巩固练习 如图,在平行四边形ABCD中,E是AB上的一点, CE和DA的延长线交于点F根据本节所得预备定理找出图中相似三角形(全等三角形除外).变式一:连接BD巩固练习 如图,在平行四边形ABCD中,E是AB上的一点, CE和DA的延长线交于点F根据本节所得预备定理找出图中相似三角形(全等三角形除外).变式二:G为BC延长线上一点G巩固练习 1.已知:如图,AB∥EF ∥CD,3图中共有____对相似三角形。 △EOF∽△COD AB∥EF △AOB∽ △FOE AB∥CDEF∥CD△AOB ∽△DOC理解请写出它们的对应边的比例式理解 1.如图,△ABC 中,DE∥BC,GF∥AB,DE、GF交于点O,则图中与△ABC相似的三角形共有多少个?请你写出来.解: 与△ABC相似的三角形有3个: △ADE
△GFC
△GOE运用2.如图,已知DE ∥ BC,AE=50cm,EC=30cm,BC=70cm,
∠BAC=450,∠ACB=400.
(1)求∠AED和∠ADE的大小;(2)求DE的长.
(2)解: (1)DE ∥ BC△ADE∽△ABC∠AED=∠C=400.△ADE∽△ABC运用在△ADE中, ∠ADE=1800-400-450=950.3.如图,在△ABC中,DG∥EH∥FI∥BC,
(1)请找出图中所有的相似三角形;
(2)如果AD=1,DB=3,那么DG:BC=_____。△ADG∽△AEH∽△AFI∽△ABC1:4运用4.有一块呈三角形形状的草坪,其中一边的长是20m,在这个草坪的图纸上,这条边长5cm,其他两边的长都是3.5cm,求该草坪其他两边的实际长度。思考下列问题:1、草坪的形状与其图纸上相应的形状是否相似? 2.它们的相似比是多少?解:设其他两边的实际长度都是xcm,则
X=3.5×400=1400cm=14m
答:草坪其他两边的实际长度都是14m运用小结
