(2022秋季新教材)人教版 五年级上册第3课时 梯形的面积 课件(共25张PPT)
文档属性
| 名称 | (2022秋季新教材)人教版 五年级上册第3课时 梯形的面积 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-05 14:39:20 | ||
图片预览



文档简介
(共25张PPT)
2022秋 人教数学
五年级上册
梯形的面积
R·五年级上册
你能用学过的方法推导出梯形的面积计算公式吗?
情景导入
车窗玻璃的形状是梯形,怎样计算它的面积呢?
回忆一下,我们是怎样推导出三角形面积的计算公式的?
三角形(新) 已学过的图形(旧)
转化(拼接、割补)
推导
联系
情景导入
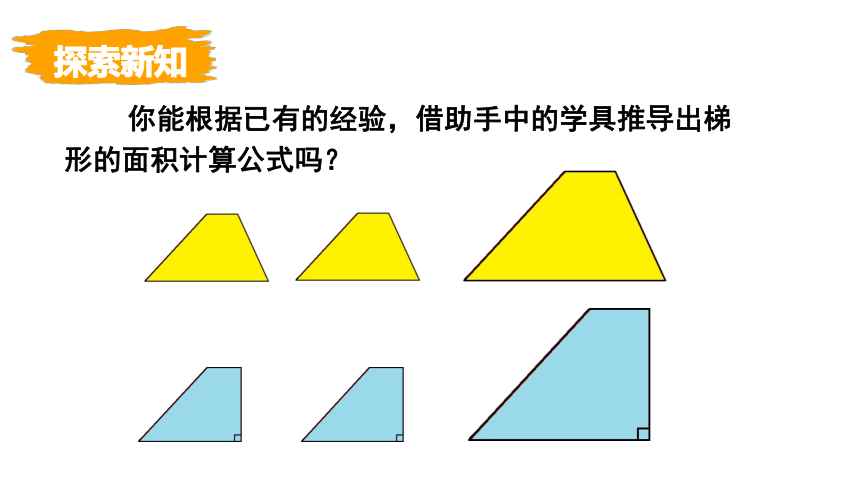
你能根据已有的经验,借助手中的学具推导出梯形的面积计算公式吗?
探索新知
操作指南:
1.想一想:你能用什么办法求出这个梯形纸片的面积?
2.做一做:可以折、拼、剪。
3.说一说:你是用什么办法求出这个梯形纸片的面积。
探索新知
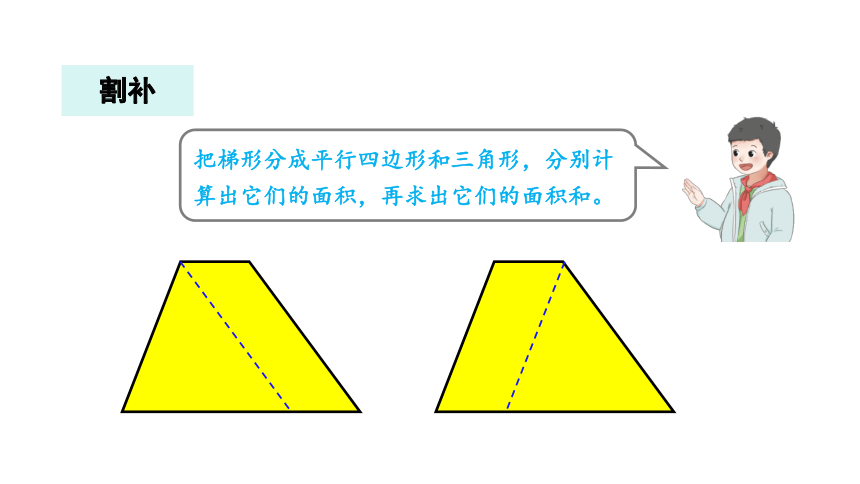
把梯形分成平行四边形和三角形,分别计算出它们的面积,再求出它们的面积和。
割补
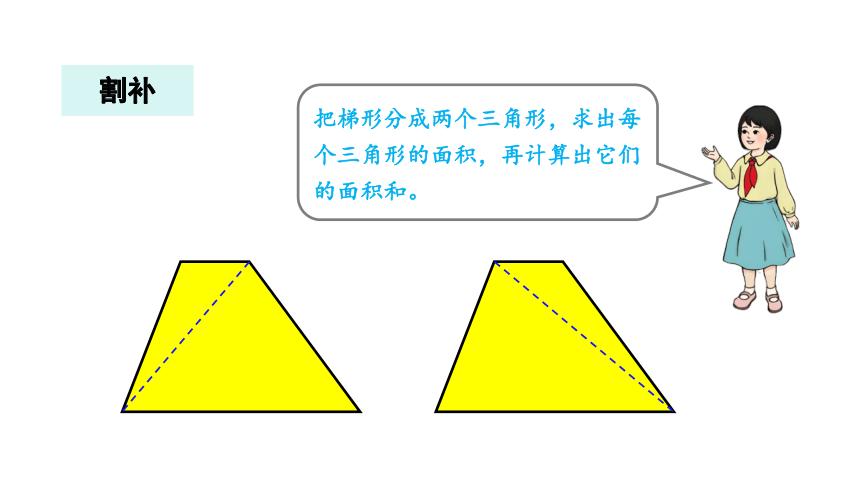
把梯形分成两个三角形,求出每个三角形的面积,再计算出它们的面积和。
割补
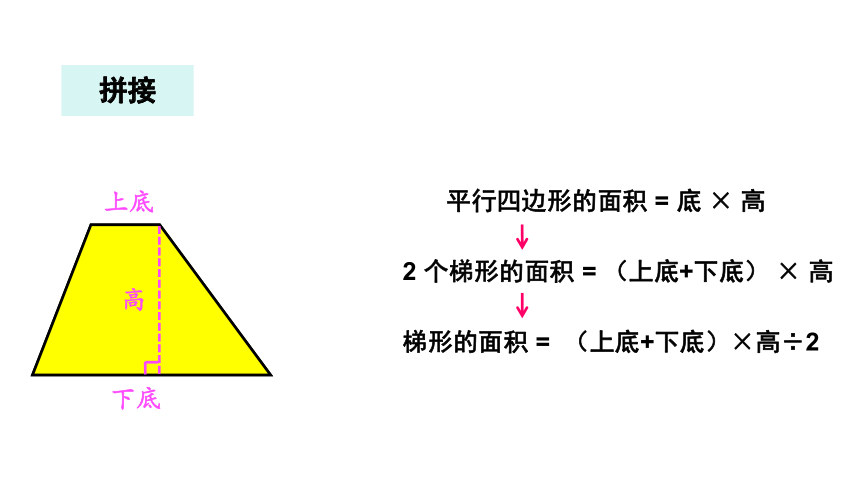
上底
下底
平行四边形的面积 = 底 × 高
2 个梯形的面积 = (上底+下底) × 高
梯形的面积 = (上底+下底)×高÷2
高
拼接
上底
下底
长方形的面积 = 长 × 宽
2 个梯形的面积 =(上底+下底)× 高
梯形的面积 = (上底+下底)×高÷2
高
拼接
方法1
方法2
方法3
梯形(新) 已学过的图形(旧)
转化(拼接、割补)
梯形的面积 =______________________
(上底+下底)×高÷2
上底
下底
高
平行四边形的面积 = 底 × 高
2 个梯形的面积 = (上底+下底) × 高
如果用 S 表示梯形的面积,用 a、b 和 h 分别表示梯形的上底、下底和高,那么梯形的面积计算公式可以写成:
b
a
h
S = (a + b)h÷2
易错点:不要忘记“÷2”。
方法1
上底
下底
高
梯形的面积 = 三角形的面积+平行四边形的面积
= 三角形的底×高÷2+平行四边形的底×高
= (三角形的底÷2+平行四边形的底÷2×2)×高
= (三角形的底+平行四边形的底×2)×高÷2
=[平行四边形的底+(三角形的底+平行四边形的底)]×高÷2
=(梯形的上底+梯形的下底)×高÷2
所以,梯形的面积=(上底+下底)×高÷2
上底
下底
方法2
梯形的面积 = 三角形①的面积+三角形②的面积
①
②
= 上底×高÷2+下底×高÷2
=(上底+下底)×高÷2
[教材P94 例3]
我国三峡水电站大坝的横截面的一部分是梯形(如下图),求它的面积。
S =(a+b)h÷2
=(36+120)×135÷2
= 156×135÷2
= 10530(m2)
答:它的面积是 10530 平方米。
一辆汽车侧面的两块玻璃的形状是梯形(如下图),它们的面积分别是多少?
[教材P94 做一做]
随堂练习
1
S =(a + b)h÷2
=(40 + 71)×40÷2
= 111×40÷2
= 2220(cm2)
S =(a + b)h÷2
=(45 + 65)×40÷2
= 110×40÷2
= 2200(cm2)
答:它们的面积分别是 2220 cm2和2200 cm2。
一条新挖的水渠,横截面是梯形(如图)。渠口宽2.8m,渠底宽1.4m,渠深1.2m。横截面的面积是多少平方米?
[教材P95 练习二十一 第1题]
(1.4 + 2.8)×1.2÷2= 2.52(m2)
答:它的横截面积是 2.52 m2。
2
一块梯形木板,上底长 10 cm,下底比上底长 7 cm,高 6 cm,这块木板的面积是多少?
(10+10+7)×6÷2 = 81(cm2)
答:这块木板的面积是 81 cm2。
3
你知道吗?
我国古代数学家刘徽利用“出入相补” 原理来计算平面图形的面积。出入相补原理是指:把一个图形分割、移补,而面积保持不变(如下图所示)。你能运用这一原理推导出三角形和梯形的面积公式吗?
通过本节课的学习,你有什么收获?
课堂小结
一、求下面梯形的面积。
(8+12)×6÷2 = 60(cm2)
(7+15)×8÷2 = 88(dm2)
巩固练习
二、一条防洪堤,横截面是梯形(如图),它的横截面的面积是多少平方米?(单位:m)
(6+25)×10÷2 = 155(m2)
三、一个梯形的面积是 28 dm2,上底是 5 dm,下底是 9 dm,它的高是多少分米?
28×2÷(5+9) = 4(dm)
2022秋 人教数学
五年级上册
梯形的面积
R·五年级上册
你能用学过的方法推导出梯形的面积计算公式吗?
情景导入
车窗玻璃的形状是梯形,怎样计算它的面积呢?
回忆一下,我们是怎样推导出三角形面积的计算公式的?
三角形(新) 已学过的图形(旧)
转化(拼接、割补)
推导
联系
情景导入
你能根据已有的经验,借助手中的学具推导出梯形的面积计算公式吗?
探索新知
操作指南:
1.想一想:你能用什么办法求出这个梯形纸片的面积?
2.做一做:可以折、拼、剪。
3.说一说:你是用什么办法求出这个梯形纸片的面积。
探索新知
把梯形分成平行四边形和三角形,分别计算出它们的面积,再求出它们的面积和。
割补
把梯形分成两个三角形,求出每个三角形的面积,再计算出它们的面积和。
割补
上底
下底
平行四边形的面积 = 底 × 高
2 个梯形的面积 = (上底+下底) × 高
梯形的面积 = (上底+下底)×高÷2
高
拼接
上底
下底
长方形的面积 = 长 × 宽
2 个梯形的面积 =(上底+下底)× 高
梯形的面积 = (上底+下底)×高÷2
高
拼接
方法1
方法2
方法3
梯形(新) 已学过的图形(旧)
转化(拼接、割补)
梯形的面积 =______________________
(上底+下底)×高÷2
上底
下底
高
平行四边形的面积 = 底 × 高
2 个梯形的面积 = (上底+下底) × 高
如果用 S 表示梯形的面积,用 a、b 和 h 分别表示梯形的上底、下底和高,那么梯形的面积计算公式可以写成:
b
a
h
S = (a + b)h÷2
易错点:不要忘记“÷2”。
方法1
上底
下底
高
梯形的面积 = 三角形的面积+平行四边形的面积
= 三角形的底×高÷2+平行四边形的底×高
= (三角形的底÷2+平行四边形的底÷2×2)×高
= (三角形的底+平行四边形的底×2)×高÷2
=[平行四边形的底+(三角形的底+平行四边形的底)]×高÷2
=(梯形的上底+梯形的下底)×高÷2
所以,梯形的面积=(上底+下底)×高÷2
上底
下底
方法2
梯形的面积 = 三角形①的面积+三角形②的面积
①
②
= 上底×高÷2+下底×高÷2
=(上底+下底)×高÷2
[教材P94 例3]
我国三峡水电站大坝的横截面的一部分是梯形(如下图),求它的面积。
S =(a+b)h÷2
=(36+120)×135÷2
= 156×135÷2
= 10530(m2)
答:它的面积是 10530 平方米。
一辆汽车侧面的两块玻璃的形状是梯形(如下图),它们的面积分别是多少?
[教材P94 做一做]
随堂练习
1
S =(a + b)h÷2
=(40 + 71)×40÷2
= 111×40÷2
= 2220(cm2)
S =(a + b)h÷2
=(45 + 65)×40÷2
= 110×40÷2
= 2200(cm2)
答:它们的面积分别是 2220 cm2和2200 cm2。
一条新挖的水渠,横截面是梯形(如图)。渠口宽2.8m,渠底宽1.4m,渠深1.2m。横截面的面积是多少平方米?
[教材P95 练习二十一 第1题]
(1.4 + 2.8)×1.2÷2= 2.52(m2)
答:它的横截面积是 2.52 m2。
2
一块梯形木板,上底长 10 cm,下底比上底长 7 cm,高 6 cm,这块木板的面积是多少?
(10+10+7)×6÷2 = 81(cm2)
答:这块木板的面积是 81 cm2。
3
你知道吗?
我国古代数学家刘徽利用“出入相补” 原理来计算平面图形的面积。出入相补原理是指:把一个图形分割、移补,而面积保持不变(如下图所示)。你能运用这一原理推导出三角形和梯形的面积公式吗?
通过本节课的学习,你有什么收获?
课堂小结
一、求下面梯形的面积。
(8+12)×6÷2 = 60(cm2)
(7+15)×8÷2 = 88(dm2)
巩固练习
二、一条防洪堤,横截面是梯形(如图),它的横截面的面积是多少平方米?(单位:m)
(6+25)×10÷2 = 155(m2)
三、一个梯形的面积是 28 dm2,上底是 5 dm,下底是 9 dm,它的高是多少分米?
28×2÷(5+9) = 4(dm)
