23.2《相似三角形的判定(一)》课件
文档属性
| 名称 | 23.2《相似三角形的判定(一)》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 247.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-03 21:48:03 | ||
图片预览




文档简介
课件23张PPT。相似三角形的判定定理(一) 相似三角形的预备定理:
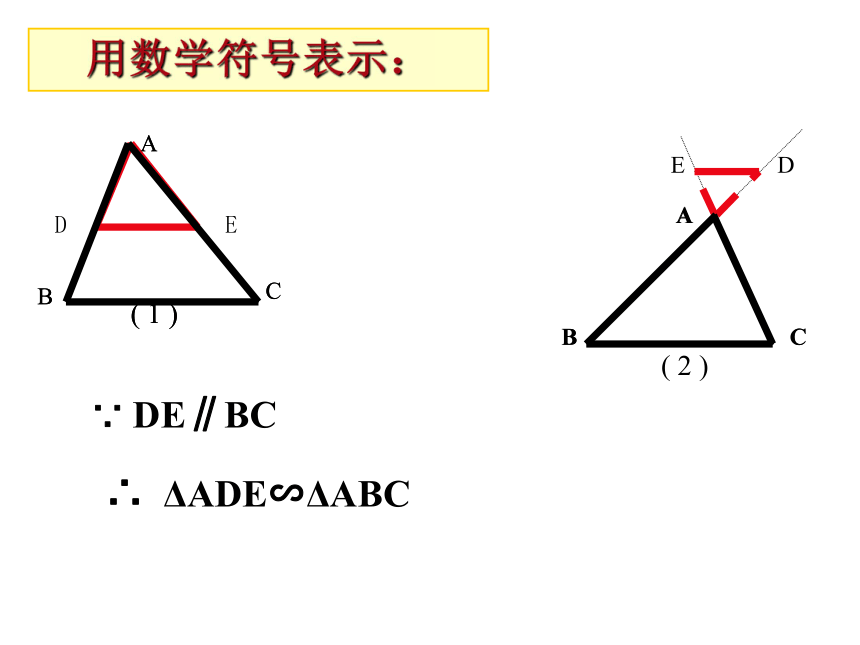
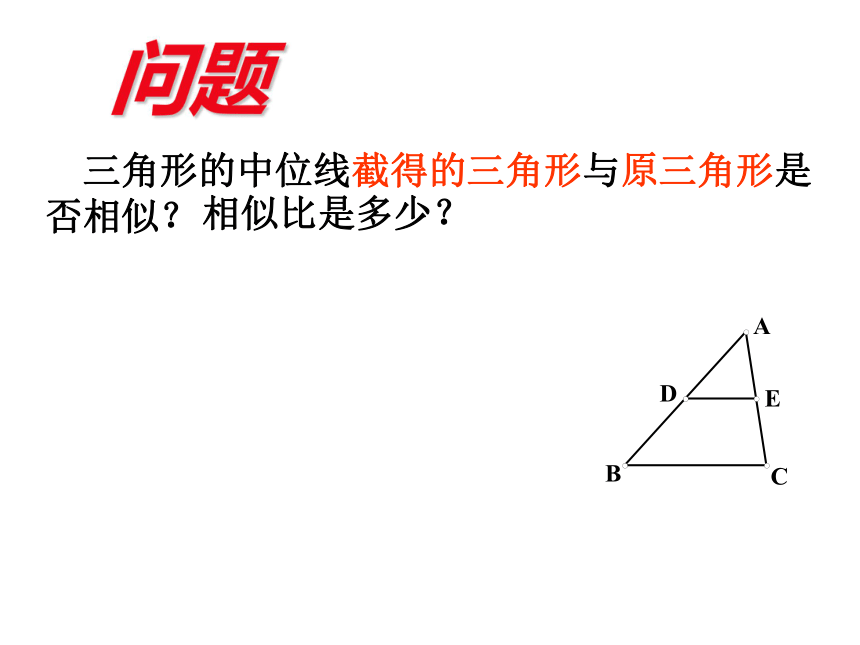
如果一条直线平行于三角形的一条边,且这条直线与原三角形的两条边 (或其延长线)分别相交,那么所构成的三 角形与原三角形相似。复习回顾DE用数学符号表示:∵ DE∥BC∴ ΔADE∽ΔABC 三角形的中位线截得的三角形与原三角形是否相似?相似比是多少?
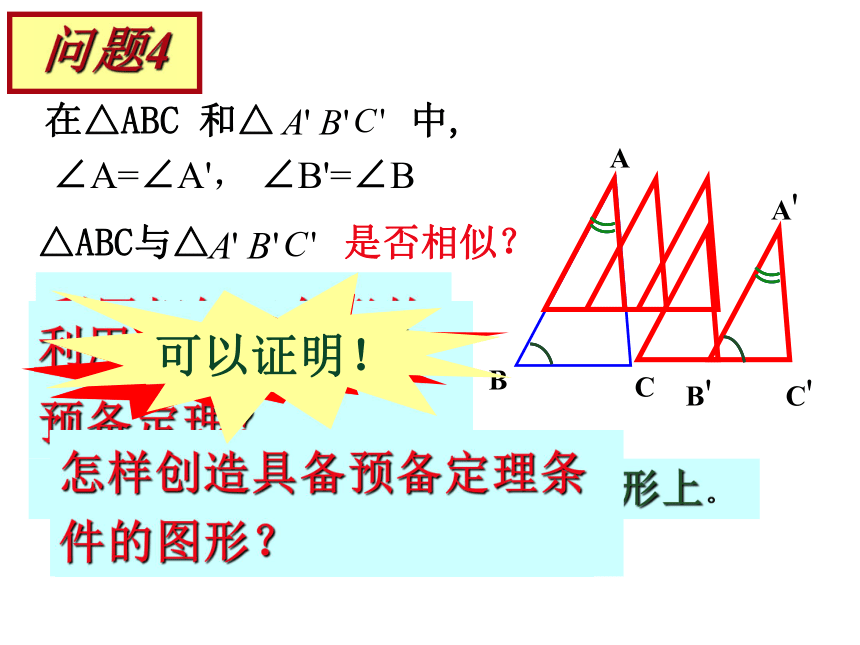
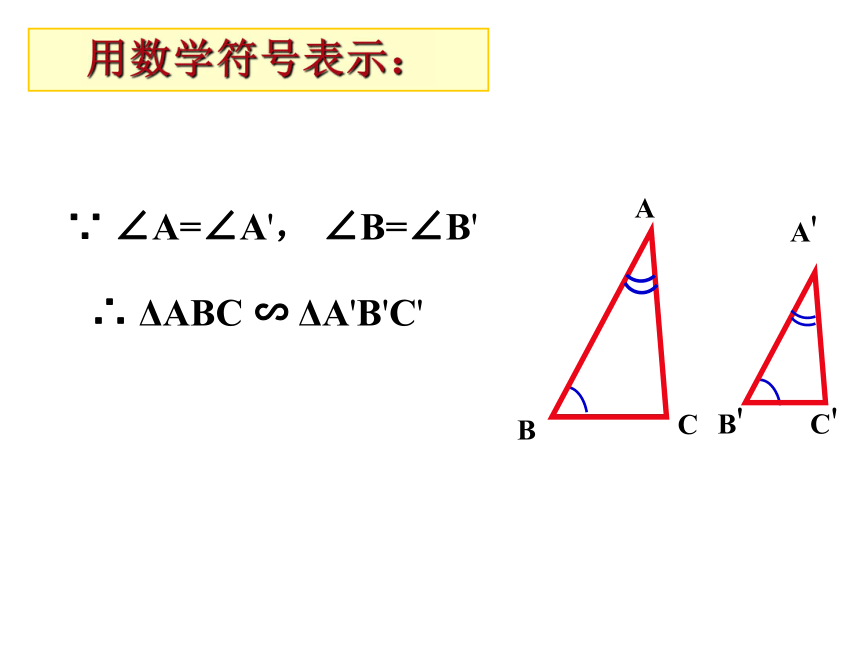
问题在△ABC 和△ 中,△ABC与△ 把小的三角形移动到大的三角形上。是否相似?利用相似三角形的定义?利用相似三角形的预备定理?怎样创造具备预备定理条件的图形? 条件不够可以证明!问题4∠A=∠A', ∠B'=∠BABCA/ C/ B/ 判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。可以简单说成:两角对应相等,两三角形相似。∵ AD=A'B',∠A=∠A',AE=A'C'∴ ΔA DE≌ΔA'B'C',∴ ∠ADE=∠B',又∵ ∠B'=∠B,∴ ∠ADE=∠B,∴ DE//BC,∴ ΔADE∽ΔABC。∴ ΔA'B'C'∽ΔABC证明:在AB,AC上分别截取AD= A'B' ,AE = A'C'CC'∵ ∠A=∠A', ∠B=∠B'∴ ΔABC ∽ ΔA'B'C'用数学符号表示:原因?相似三角形的传递性:如果△ABC∽△A1B1C1 ,
而△A1B1C1 ∽△A2B2C2
那么△ABC∽△A2B2C2 。如果△ABC∽△A1B1C1
而△A1B1C1 ∽△A2B2C2
那么△ABC与△A2B2C2
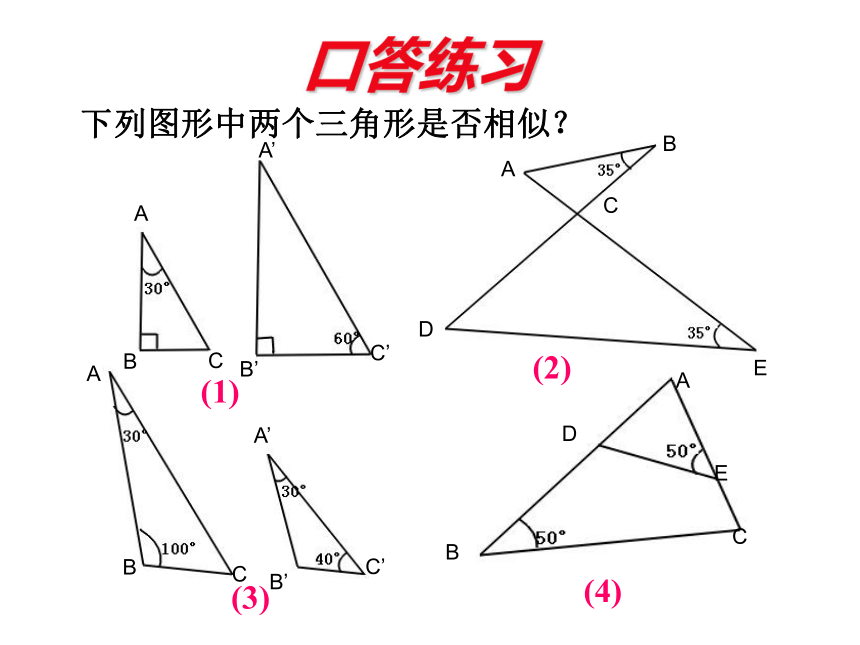
是否相似? 问题下列图形中两个三角形是否相似?(1)(2)(3)(4)口答练习
⑴所有的直角三角形都相似 . ( )
⑵有一个锐角对应相等的两直角三角形相似.( )
⑶所有的等边三角形都相似. ( )
⑷所有的等腰直角三角形都相似. ( )
⑸顶角相等的两个等腰三角形相似. ( )
⑹有一个角相等的两个等腰三角形相似. ( )
×√√ √√×判断练习(1)ΔABC和ΔDEF中, ∠A=400,∠B=800,∠E=800, ∠F=600。ΔABC与ΔDEF (“相似”或“不相似”)。 巩固练习相似相似(3)在ΔABC中,AB?AC,D为AB边上的一点,过D点作直线DE,交边AC于E点,使ΔADE和ΔABC相似,这样的直线可以作 条2(4)有一个角相等的两等腰三角形是否为相似
三角形?顶角相等底角相等顶角与底角相等巩固练习第一种情况∴ ΔABC ∽ ΔA'B'C'第二种情况∴ ΔABC ∽ ΔA'B'C'第三种情况两三角形不相似11.已知DE ∥BC 且∠1=∠B , 则图中共有 对相似三角形。∵ DE∥BC∴△ADE∽△ABC∵ ∠1=∠B ,∠A=∠A ∴△ACD∽△ABC∴△ADE∽△ABC∽ △ACD∵ DE∥BC∵ ∠EDC=∠DCB, 又∵ ∠1=∠B∴△DEC∽△CDB4思考练习2.如图C是线段BD上的一点,AB⊥BD.ED⊥BD.AC⊥EC
求证:△ABC∽△CDEE证明:
∵AB⊥BD、ED⊥BD
∴∠ABC=∠CDE=90°
∴∠1+∠A=90°
∵AC⊥EC
∴∠1+∠2=90°
∴∠A=∠2
∴△ABC∽△CDE思考练习 3.直角三角形被斜边上的高分成的两个直角三角形和原三角形相似.已知:如图, Rt△ABC中,CD是斜边的高.求证:△ABC ∽ △CBD ∽ △ACD证明: ∵ ∠B= ∠B,
∠CDB= ∠ACB=90°
∴ ΔABC∽ΔCBD
同理 ΔABC∽ΔACD
∴ ΔABC∽ΔCBD∽ΔACD
思考练习 变式一:如图,直线a、直线b相交于点A,点B、C分别在直线a、直线b上,在直线a、直线b上分别找两点D、E,使?BAC与?DAE相似,请尽量多地画出点D、E的位置.E变式二:如图,G是□ ABCD的CD延长线上的一点,连结BG交对角线AC于E,交AD于F,则: (1)图中与△AEF相似的三角形有 .(2)图中与△ABC相似的三角形有 .(3)图中与△GFD相似的三角形有 . △CEB △CDA 、△BFA解后反思:运用定理一判定两三角形相似,如何找准两对相等的角△GBC1.已知:如图,AB ∥A’B’、BC ∥B’C’。
求证:△OAC∽△OA’C’达标练习2.已知:直线BE,DC交于A,∠E=∠C.
求证:DA·AC=BA·AE.
如果一条直线平行于三角形的一条边,且这条直线与原三角形的两条边 (或其延长线)分别相交,那么所构成的三 角形与原三角形相似。复习回顾DE用数学符号表示:∵ DE∥BC∴ ΔADE∽ΔABC 三角形的中位线截得的三角形与原三角形是否相似?相似比是多少?
问题在△ABC 和△ 中,△ABC与△ 把小的三角形移动到大的三角形上。是否相似?利用相似三角形的定义?利用相似三角形的预备定理?怎样创造具备预备定理条件的图形? 条件不够可以证明!问题4∠A=∠A', ∠B'=∠BABCA/ C/ B/ 判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。可以简单说成:两角对应相等,两三角形相似。∵ AD=A'B',∠A=∠A',AE=A'C'∴ ΔA DE≌ΔA'B'C',∴ ∠ADE=∠B',又∵ ∠B'=∠B,∴ ∠ADE=∠B,∴ DE//BC,∴ ΔADE∽ΔABC。∴ ΔA'B'C'∽ΔABC证明:在AB,AC上分别截取AD= A'B' ,AE = A'C'CC'∵ ∠A=∠A', ∠B=∠B'∴ ΔABC ∽ ΔA'B'C'用数学符号表示:原因?相似三角形的传递性:如果△ABC∽△A1B1C1 ,
而△A1B1C1 ∽△A2B2C2
那么△ABC∽△A2B2C2 。如果△ABC∽△A1B1C1
而△A1B1C1 ∽△A2B2C2
那么△ABC与△A2B2C2
是否相似? 问题下列图形中两个三角形是否相似?(1)(2)(3)(4)口答练习
⑴所有的直角三角形都相似 . ( )
⑵有一个锐角对应相等的两直角三角形相似.( )
⑶所有的等边三角形都相似. ( )
⑷所有的等腰直角三角形都相似. ( )
⑸顶角相等的两个等腰三角形相似. ( )
⑹有一个角相等的两个等腰三角形相似. ( )
×√√ √√×判断练习(1)ΔABC和ΔDEF中, ∠A=400,∠B=800,∠E=800, ∠F=600。ΔABC与ΔDEF (“相似”或“不相似”)。 巩固练习相似相似(3)在ΔABC中,AB?AC,D为AB边上的一点,过D点作直线DE,交边AC于E点,使ΔADE和ΔABC相似,这样的直线可以作 条2(4)有一个角相等的两等腰三角形是否为相似
三角形?顶角相等底角相等顶角与底角相等巩固练习第一种情况∴ ΔABC ∽ ΔA'B'C'第二种情况∴ ΔABC ∽ ΔA'B'C'第三种情况两三角形不相似11.已知DE ∥BC 且∠1=∠B , 则图中共有 对相似三角形。∵ DE∥BC∴△ADE∽△ABC∵ ∠1=∠B ,∠A=∠A ∴△ACD∽△ABC∴△ADE∽△ABC∽ △ACD∵ DE∥BC∵ ∠EDC=∠DCB, 又∵ ∠1=∠B∴△DEC∽△CDB4思考练习2.如图C是线段BD上的一点,AB⊥BD.ED⊥BD.AC⊥EC
求证:△ABC∽△CDEE证明:
∵AB⊥BD、ED⊥BD
∴∠ABC=∠CDE=90°
∴∠1+∠A=90°
∵AC⊥EC
∴∠1+∠2=90°
∴∠A=∠2
∴△ABC∽△CDE思考练习 3.直角三角形被斜边上的高分成的两个直角三角形和原三角形相似.已知:如图, Rt△ABC中,CD是斜边的高.求证:△ABC ∽ △CBD ∽ △ACD证明: ∵ ∠B= ∠B,
∠CDB= ∠ACB=90°
∴ ΔABC∽ΔCBD
同理 ΔABC∽ΔACD
∴ ΔABC∽ΔCBD∽ΔACD
思考练习 变式一:如图,直线a、直线b相交于点A,点B、C分别在直线a、直线b上,在直线a、直线b上分别找两点D、E,使?BAC与?DAE相似,请尽量多地画出点D、E的位置.E变式二:如图,G是□ ABCD的CD延长线上的一点,连结BG交对角线AC于E,交AD于F,则: (1)图中与△AEF相似的三角形有 .(2)图中与△ABC相似的三角形有 .(3)图中与△GFD相似的三角形有 . △CEB △CDA 、△BFA解后反思:运用定理一判定两三角形相似,如何找准两对相等的角△GBC1.已知:如图,AB ∥A’B’、BC ∥B’C’。
求证:△OAC∽△OA’C’达标练习2.已知:直线BE,DC交于A,∠E=∠C.
求证:DA·AC=BA·AE.
