23.2《相似三角形的判定(二)》课件
文档属性
| 名称 | 23.2《相似三角形的判定(二)》课件 |  | |
| 格式 | zip | ||
| 文件大小 | 333.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-03 21:47:37 | ||
图片预览




文档简介
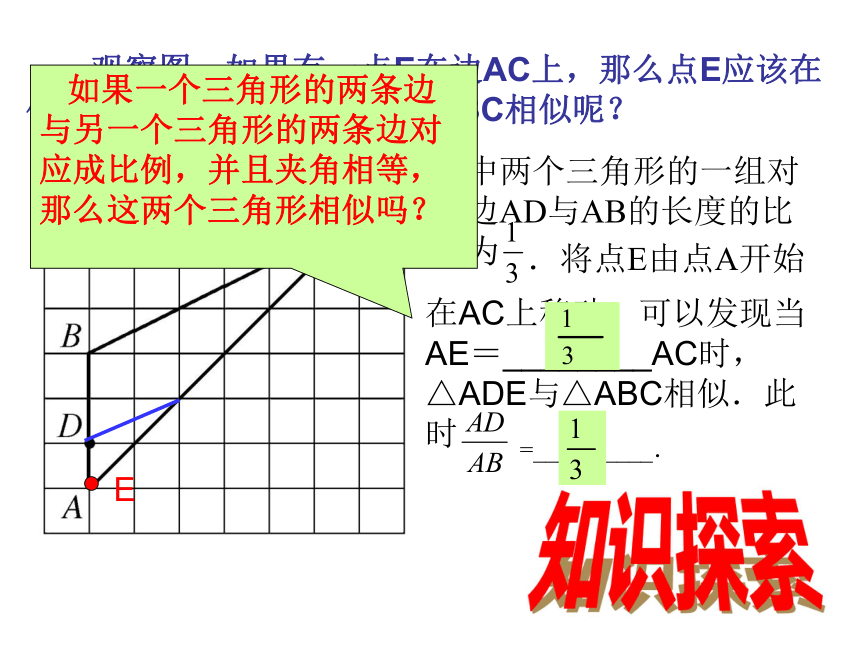
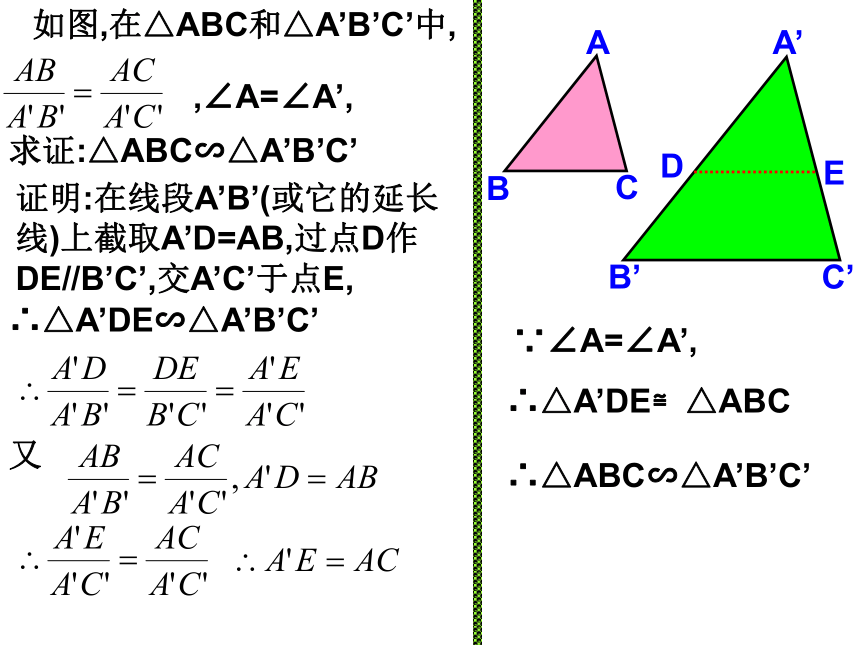
课件16张PPT。相似三角形的判定定理(二) 观察图,如果有一点E在边AC上,那么点E应该在什么位置才能使△ADE与△ABC相似呢? 如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似吗?知识探索如图,在△ABC和△A’B’C’中,求证:△ABC∽△A’B’C’证明:在线段A’B’(或它的延长线)上截取A’D=AB,过点D作DE//B’C’,交A’C’于点E,DE∴△A’DE∽△A’B’C’又∵∠A=∠A’,∴△A’DE≌△ABC∴△ABC∽△A’B’C’,∠A=∠A’, 定理2:如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似。结 论可以简单说成:两边对应成比例且夹角相等,两三角形相似。在△ABC和△A’B’C’中,∴△ABC∽△A’B’C’∠A=∠A’,思 考 对于△ABC和△A’B’C’,如果
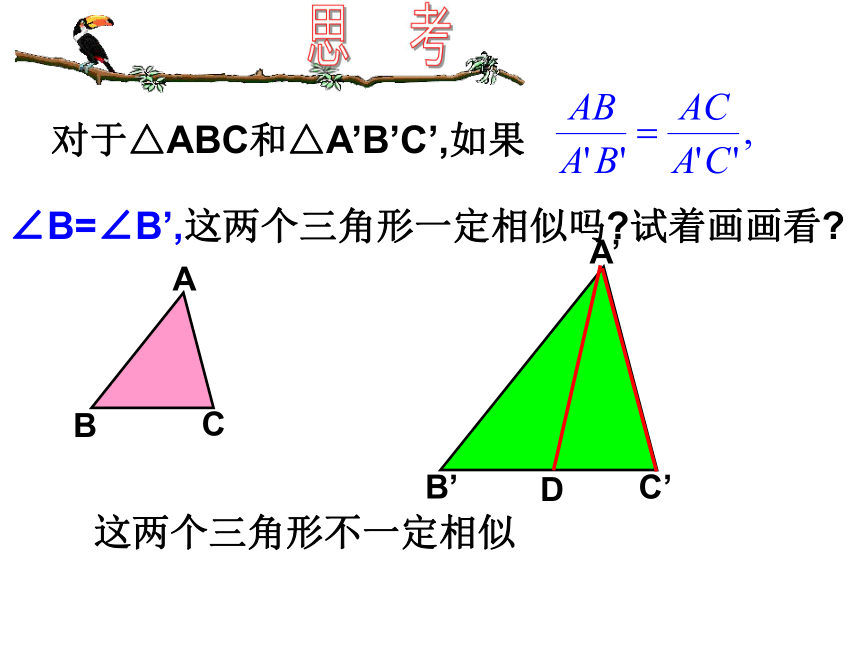
∠B=∠B’,这两个三角形一定相似吗?试着画画看?
这两个三角形不一定相似D例题解析例1: 证明图中△AEB和
△FEC相似.证明 ∵ ,
∴ ∴ △AEB∽△FEC(如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似). ∵ ∠AEB=∠FEC, 例 2:如图矩形ABCD是由三个正方形, ABEG,GEFH,
HFCD组成的,找出图中的相似三角形.解:△ AEF∽ △CEA.理由是:
设小正方形的边长是1,由勾股定理得∵∠ AEF = ∠CEA=135°.∴△ AEF ∽ △CEA.想一想1. 在△ABC中,D﹑E分别在AB﹑AC上,请你加一个条件使△ADE∽△ABC,这个条件可以是___________DE∥BC2.下列说法中错误的是( )
(A)有一个角是30°的两个等腰三角形相似
(B)有一个角是60°的两个等腰三角形相似
(C)有一个角是90°的两个等腰三角形相似
(D)有一个角是120°的两个等腰三角形相似
想一想1.如下图所示,在△ABC中,D﹑E分别在AC﹑AB上,
且AD:AB=AE:AC=1:2,BC=5,则DE=________ 2.如图,在4×4的正方形方格中,△ABC和△DEF
的顶点都在边长为1的小正方形的顶点上.
(1)填空:∠ABC= °, ∠DEF= ° ;
(2)判断△ABC与△DEF是否相似,并证明你的结论.练一练1. 根据下列条件,判断△ABC和△A’B’C’是否相似,并说明理由:
∠A=120°,AB=7cm,AC=14cm,
∠A’=120°,A’B’=3cm,A’C’=6cm,
2.如图,在△ABC中,D在AC上,已知AD=2 cm,AB=4cm,AC=8cm, 求证:△ABD∽△ABC. 达标练习 3. 如图,在正方形ABCD中,已知P是BC上的 点,且BP=3PC,Q是CD的中点,试判断△ADQ∽△QCP吗?说明理由.4.如图,在△ABC中,D在AC上,已知
AD=2 cm,AB=4cm,AC=8cm, 求证:△ABD∽△ABC.
5.如图AB=4,AC=5,CD=3,BE=6
求证: △ADE∽△ABC D6.已知△ABC 中∠C=90°,D、E分别是AB、AC上的点且AD·AB= AE·AC
求证:ED⊥AB7.如图已知:△ABC 中∠A=90°AH⊥BC
与H再以AB,AC为边向外作等边三角形
△ABD 和△ACE
求证: △BDH∽△AEH
∠B=∠B’,这两个三角形一定相似吗?试着画画看?
这两个三角形不一定相似D例题解析例1: 证明图中△AEB和
△FEC相似.证明 ∵ ,
∴ ∴ △AEB∽△FEC(如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似). ∵ ∠AEB=∠FEC, 例 2:如图矩形ABCD是由三个正方形, ABEG,GEFH,
HFCD组成的,找出图中的相似三角形.解:△ AEF∽ △CEA.理由是:
设小正方形的边长是1,由勾股定理得∵∠ AEF = ∠CEA=135°.∴△ AEF ∽ △CEA.想一想1. 在△ABC中,D﹑E分别在AB﹑AC上,请你加一个条件使△ADE∽△ABC,这个条件可以是___________DE∥BC2.下列说法中错误的是( )
(A)有一个角是30°的两个等腰三角形相似
(B)有一个角是60°的两个等腰三角形相似
(C)有一个角是90°的两个等腰三角形相似
(D)有一个角是120°的两个等腰三角形相似
想一想1.如下图所示,在△ABC中,D﹑E分别在AC﹑AB上,
且AD:AB=AE:AC=1:2,BC=5,则DE=________ 2.如图,在4×4的正方形方格中,△ABC和△DEF
的顶点都在边长为1的小正方形的顶点上.
(1)填空:∠ABC= °, ∠DEF= ° ;
(2)判断△ABC与△DEF是否相似,并证明你的结论.练一练1. 根据下列条件,判断△ABC和△A’B’C’是否相似,并说明理由:
∠A=120°,AB=7cm,AC=14cm,
∠A’=120°,A’B’=3cm,A’C’=6cm,
2.如图,在△ABC中,D在AC上,已知AD=2 cm,AB=4cm,AC=8cm, 求证:△ABD∽△ABC. 达标练习 3. 如图,在正方形ABCD中,已知P是BC上的 点,且BP=3PC,Q是CD的中点,试判断△ADQ∽△QCP吗?说明理由.4.如图,在△ABC中,D在AC上,已知
AD=2 cm,AB=4cm,AC=8cm, 求证:△ABD∽△ABC.
5.如图AB=4,AC=5,CD=3,BE=6
求证: △ADE∽△ABC D6.已知△ABC 中∠C=90°,D、E分别是AB、AC上的点且AD·AB= AE·AC
求证:ED⊥AB7.如图已知:△ABC 中∠A=90°AH⊥BC
与H再以AB,AC为边向外作等边三角形
△ABD 和△ACE
求证: △BDH∽△AEH
