苏教版(2019)高中数学必修一第6章 幂函数、指数函数和对数函数综合拔高练(Word含答案)
文档属性
| 名称 | 苏教版(2019)高中数学必修一第6章 幂函数、指数函数和对数函数综合拔高练(Word含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 197.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-06 15:50:14 | ||
图片预览




文档简介
第6章 幂函数、指数函数和对数函数综合拔高练
考点1 比较大小
1.(2021新高考Ⅱ,7)若a=log52,b=log83,c=,则( )
A.c2.(2021天津,5)设a=log20.3,b=lo0.4,c=0.40.3,则a,b,c的大小关系为( )
A.a3.(2019课标全国Ⅲ,11)设f(x)是定义域为R的偶函数,且在(0,+∞)单调递减,则( )
A. f >f()>f()
B. f >f()>f()
C. f()>f()>f
D. f()>f()>f
考点2 幂函数、指数函数、对数函数的图象
4.(2021天津,3)函数y=的图象大致为( )
5.(2020北京,6)已知函数f(x)=2x-x-1,则不等式f(x)>0的解集是( )
A.(-1,1)
B.(-∞,-1)∪(1,+∞)
C.(0,1)
D.(-∞,0)∪(1,+∞)
6.(2019课标全国Ⅲ,7)函数y=在[-6,6]上的图象大致为( )
7.(2018课标全国Ⅲ,7)下列函数中,其图象与函数y=ln x的图象关于直线x=1对称的是( )
A.y=ln(1-x) B.y=ln(2-x)
C.y=ln(1+x) D.y=ln(2+x)
8.(2018课标全国Ⅱ,3)函数f(x)=的图象大致为( )
A B C D
考点3 幂函数、指数函数、对数函数的性质
9.(2020全国Ⅰ理,12)若2a+log2a=4b+2log4b,则( )
A.a>2b B.a<2b C.a>b2 D.a10.(2020全国Ⅱ文,10)设函数f(x)=x3-,则f(x)( )
A.是奇函数,且在(0,+∞)单调递增
B.是奇函数,且在(0,+∞)单调递减
C.是偶函数,且在(0,+∞)单调递增
D.是偶函数,且在(0,+∞)单调递减
11.(2020全国Ⅱ理,9)设函数f(x)=ln|2x+1|-ln|2x-1|,则f(x)( )
A.是偶函数,且在单调递增
B.是奇函数,且在单调递减
C.是偶函数,且在单调递增
D.是奇函数,且在单调递减
12.(2021新高考Ⅰ,13)已知函数f(x)=x3(a·2x-2-x)是偶函数,则a= .
13.(2020北京,11)函数f(x)=+ln x的定义域是 .
14.(2020江苏,7)已知y=f(x)是奇函数,当x≥0时, f(x)=,则f(-8)的值是 .
考点4 反函数
(2020上海,4)已知函数f(x)=x3,f -1(x)是f(x)的反函数,则
f -1(x)= .
16.(2018上海,4)设常数a∈R,函数f(x)=log2(x+a).若f(x)的反函数的图象经过点(3,1),则a= .
应用实践
1.(2021江苏泰州期末)设函数f(x)=则满足不等式f(x)+f>2的x的取值范围是( )
A. B.
C. D.
2.(2021河南驻马店期末)设函数y=f(x)和y=f(-x),若两函数在区间[m,n]上的单调性相同,则把区间[m,n]叫作y=f(x)的“稳定区间”.已知区间[1,2 021]为函数g(x)=的“稳定区间”,则实数a的可能取值是( )
A.- B.- C. D.-4
3.(2021江苏南通如东高级中学期末)已知f(x)=若关于x的方程f(x)=m(m∈R)有四个不相等的实根x1,x2,x3,x4,则x1x2x3x4的取值范围是( )
A. B.
C. D.
4.(2022江苏马坝高级中学阶段检测)已知函数f(x)对于一切实数x,y均有f(x+y)-f(y)=x(x+2y+1)成立,且f(1)=0,则当x∈时,不等式f(x)+2A.∪(1,+∞) B.
C.∪(1,+∞) D.
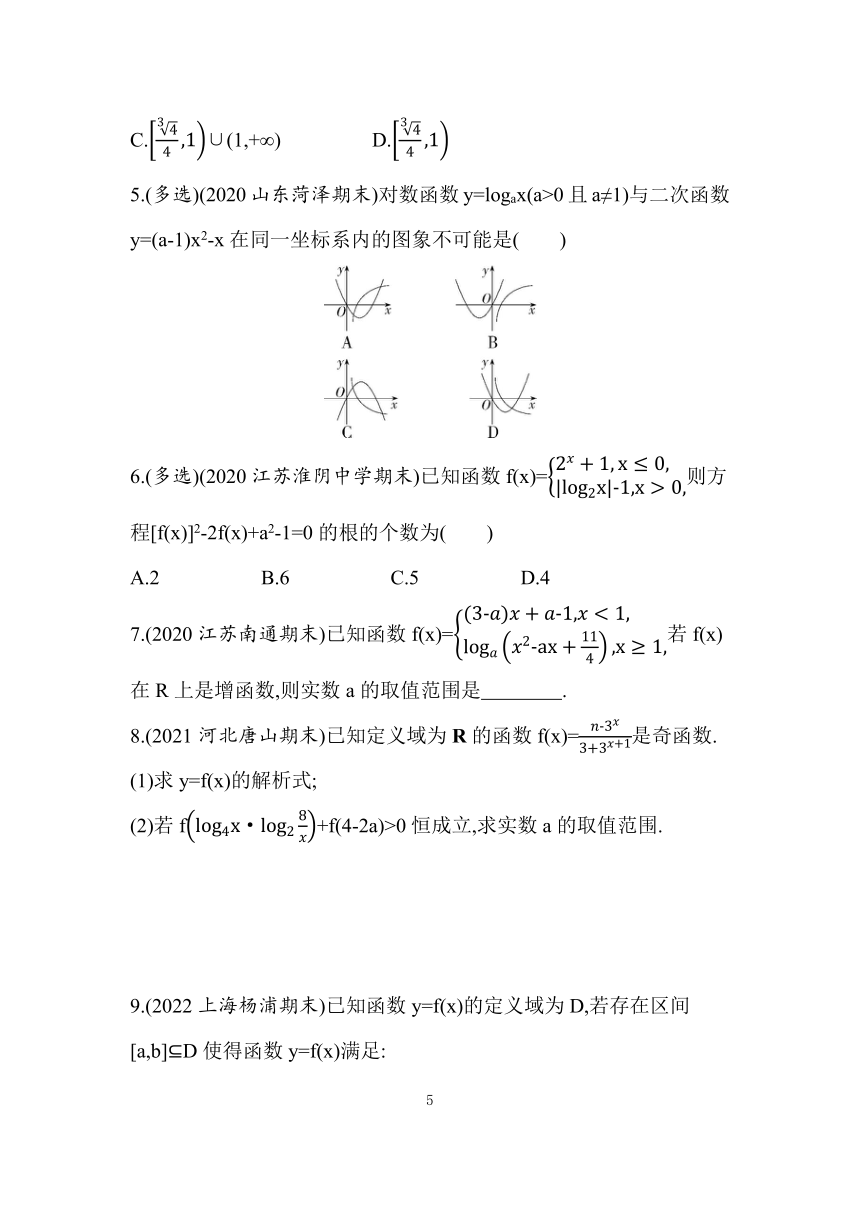
5.(多选)(2020山东菏泽期末)对数函数y=logax(a>0且a≠1)与二次函数y=(a-1)x2-x在同一坐标系内的图象不可能是( )
6.(多选)(2020江苏淮阴中学期末)已知函数f(x)=则方程[f(x)]2-2f(x)+a2-1=0的根的个数为( )
A.2 B.6 C.5 D.4
7.(2020江苏南通期末)已知函数f(x)=若f(x)在R上是增函数,则实数a的取值范围是 .
8.(2021河北唐山期末)已知定义域为R的函数f(x)=是奇函数.
(1)求y=f(x)的解析式;
(2)若f+f(4-2a)>0恒成立,求实数a的取值范围.
9.(2022上海杨浦期末)已知函数y=f(x)的定义域为D,若存在区间[a,b] D使得函数y=f(x)满足:
①函数y=f(x)在区间[a,b]上是严格增函数或严格减函数;
②函数y=f(x),x∈[a,b]的值域是[na,nb](n∈Z且n≥2).
则称区间[a,b]为函数y=f(x)的“n倍区间”.
(1)判断下列函数是否存在“2倍区间”(不需要说明理由);
①y=1-x;②y=x2+;
(2)证明:函数y=x-2不存在“n倍区间”;
(3)证明:当有理数m满足m∈(0,1)∪(1,+∞)时,对任意n(n∈Z且n≥2),函数y=xm都存在“n倍区间”,并求函数y=x3和y=所有的“10倍区间”.
答案全解全析
1.C 2.D 3.C 4.B 5.D 6.B 7.B 8.B
9.B 10.A 11.D
1.C ∵log52log8,
∴b>c,∴a2.D ∵a=log20.3lo=1,∴a<1,b>1.
∵0<0.40.3<0.40=1,∴03.C ∵f(x)是定义域为R的偶函数,
∴f(-x)=f(x),∴f=f(-log34)=f(log34).
∵log34>log33=1,且1>>>0,
∴log34>>>0.
∵f(x)在(0,+∞)上单调递减,
∴f()>f(.故选C.
4.B 设f(x)=,则f(x)的定义域为{x|x≠0},
因为f(-x)=>0,排除D,故选B.
5.D 不等式f(x)>0等价于不等式2x>x+1,作出函数y=2x和函数y=x+1的图象,如图所示,易知两个函数图象的交点坐标为(1,2)和(0,1),观察函数图象可知,当x>1或x<0时,函数y=2x的图象在函数y=x+1图象的上方,此时2x>x+1,故不等式f(x)>0的解集为(-∞,0)∪(1,+∞),故选D.
6.B 设f(x)=(x∈[-6,6]),则f(-x)=≈7.97,排除选项A.故选B.
7.B 设所求函数图象上一点的坐标为(a,b),则点(a,b)关于直线x=1的对称点(2-a,b)在函数y=ln x的图象上,∴b=ln(2-a),故所求的函数为y=ln(2-x).
8.B 因为f(x)的定义域关于原点对称且f(-x)=-f(x),所以f(x)为奇函数,排除A选项;
f(2)=>1,排除C、D选项.故选B.
9.B 2a+log2a=22b+log2b<22b+log2(2b),令f(x)=2x+log2x,则f(a)10.A 由函数y=x3和y=-
是奇函数,且在区间(0,+∞)上单调递增.故选A.
11.D x∈xx≠ ±,x∈R,∴函数f(x)的定义域关于原点对称,又∵f(-x)=ln|-2x+1|-ln|-2x-1|=ln|2x-1|-ln|2x+1|=-f(x),∴f(x)是奇函数,排除A、C;当x∈时,f(x)=ln(2x+1)-ln(1-2x),
∵y=ln(2x+1)在上单调递减,
∴f(x)在上单调递增,排除B;当x∈上单调递减,∴D正确.
12.答案 1
解析 ∵f(x)=x3(a·2x-2-x)为偶函数,
∴f(1)=f(-1),
∴2a-,∴a=1.
当a=1时,f(x)=x3(2x-2-x),定义域为R,且满足f(-x)=f(x),即f(x)为偶函数.
13.答案 (0,+∞)
解析 要使函数f(x)有意义,则故x>0,
因此函数f(x)的定义域为(0,+∞).
14.答案 -4
解析 由函数f(x)是奇函数得f(-8)=-f(8)=-=-4.
15.答案
解析 由f(x)=x3,得x=.
16.答案 7
解析 ∵f(x)的反函数的图象经过点(3,1),∴函数f(x)=log2(x+a)的图象经过点(1,3),
∴log2(1+a)=3,解得a=7.
1.D 2.B 3.D 4.D 5.BCD 6.ACD
1.D 当x-时,不等式显然成立;
当x≤1时,f(x)+f当x>1且x-≤1,即12.
综上,不等式的解集为.故选D.
2.B g(x)=,则g(-x)=|3x+a|.
①当两个函数都是增函数时,
在区间[1,2 021]上恒成立,即(-3x)max≤a≤,所以-3≤a≤-;
②当两个函数都是减函数时,在区间[1,2 021]上恒成立,即≤a≤(-3x)min,无解.综上,-3≤a≤-.
故选B.
3.D 画出函数f(x)的图象,如图所示:
由图可知,方程f(x)=m有四个不相等的实根时2≤m<.
设y=m与y=2-3x-2x2=-2(x≤0)图象的交点的横坐标从左到右为x1,x2,则x1<0,x2≤0,且x1+x2=-,x1x2≥0,
∴x1x2=(-x1)(-x2)<.
设y=m与y=|lg x|(x>0)图象的交点的横坐标从左到右为x3,x4,则x3>0,x4>0.
由|lg x3|=|lg x4|得lg x3=-lg x4,
∴x3x4=1.
∴x1x2x3x4∈.
故选D.
4.D 令x=1,y=0,则f(1)-f(0)=2,
∵f(1)=0,
∴f(0)=-2,
令y=0,则f(x)-f(0)=x(x+1),即f(x)=x2+x-2.
当x∈时,不等式f(x)+2∴当x∈时,x2+x令g(x)=x2+x,x∈上单调递增,
∴g(x)∈,
要使x2+x1时,logax<0,不成立;
当05.BCD 选项A,B中,由对数函数图象得a>1,则二次函数中二次项系数a-1>0,其对应方程的两个根为0,<0,与a>1相矛盾,选项B不可能.
选项C,D中,由对数函数的图象得01,与0解题模板
确定含参数的函数的图象,要分析函数中参数的几何意义.特别是二次函数中,要从图象的开口方向、对称轴、与x轴的交点位置等方面进行分析,对各个选项逐一进行判断
6.ACD 画出f(x)的图象,如图所示:
令t=f(x),则t2-2t+a2-1=0,Δ=4(2-a2).
当Δ=0,即a2=2时,t=1,此时f(x)=1,由图可知,直线y=1与y=f(x)的图象有2个交点,
所以方程[f(x)]2-2f(x)+a2-1=0的根的个数为2,A正确.
当Δ>0,即a2<2时,t=1±≤≤1+≤1-<1.
当t=1-时,f(x)∈[1-,1),由图可知x有2个解;
当t=1+时,若t∈(1,2],则x有3个解;若t∈(2,1+],则x有2个解.
故方程[f(x)]2-2f(x)+a2-1=0的根的个数为5或4,C、D正确.故选ACD.
7.答案
解析 因为函数f(x)在R上是增函数,
所以y=(3-a)x+a-1在区间(-∞,1)上是增函数且y=loga在区间[1,+∞)上也是增函数.
由函数y=(3-a)x+a-1在(-∞,1)上是增函数,得3-a>0 a<3.①
对于函数y=loga,x∈[1,+∞),令u=x2-ax+=.
当0又y=logau为定义域内的减函数,
所以根据复合函数“同增异减”可得0当a>1时,要使函数y=loga=在[1,+∞)上也是增函数,又对数函数的真数大于0,
所以解得a≤2,
又a>1,所以1由①②得1因为f(x)在R上是增函数,所以f(x)的图象在衔接点处的函数值应满足3-a+a-1≤
loga,
即a2+a-≤0,解得-≤a≤.
所以实数a的取值范围是.
8.解析 (1)因为函数f(x)=为奇函数,
所以f(-x)=-f(x),
即,
所以,
所以n·3x-1=-n+3x,
即(n-1)(3x+1)=0,解得n=1.
故函数f(x)=.
(2)由(1)知f(x)=·,
所以f(x)在(-∞,+∞)上单调递减.
由f>-f(4-2a).
因为函数f(x)是奇函数,
所以f>f(2a-4),
所以log4x·(3-log2x)<2a-4,
整理得log2x·(3-log2x)<2a-4.
设t=log2x,t∈R,则(3t-t2)<2a-4恒成立,
令y=.
9.解析 (1)y=1-x不存在“2倍区间”,y=x2+存在“2倍区间”.
理由如下:根据严格单调定义可知,函数y=1-x在R上严格单调递减,若[a,b]是函数的2倍区间,则函数的值域为[1-b,1-a],且,不满足a易知函数y=x2+
∴
即函数y=x2+.
(2)证明:假设存在区间[a,b]是y=x-2的“n倍区间”(n∈Z,且n≥2),
由条件①可知,[a,b] (-∞,0)或[a,b] (0,+∞).当[a,b] (0,+∞),即0因为y=在(0,+∞)上是严格减函数,
所以
所以=1,即a=b,
这与a即y=x-2在x∈(0,+∞)上不存在“n倍区间”,
当[a,b] (-∞,0)时,[na,nb] (-∞,0),
这与x∈(-∞,0)时,y=x-2>0矛盾,
即y=x-2在x∈(-∞,0)上不存在“n倍区间”.
综上所述,函数y=x-2不存在“n倍区间”.
(3)先考虑y=xm,x∈[0,+∞)的情况,
因为y=xm在[0,+∞)上是严格增函数,所以若存在“n倍区间”,则xm=nx有两个非负解,方程xm=nx可化为x(xm-1-n)=0,
当m∈(0,1)∪(1,+∞)时,方程xm=nx有两个非负解x=0和x=,
所以至少存在一个“n倍区间”为[0,].
y=x3在(-∞,+∞)是严格增函数,
令x3=10x,解得x1=0,x2=,
所以y=x3有三个“10倍区间”,分别是[-].
y=在[0,+∞)上是严格增函数,在(-∞,0]上是严格减函数,
当x∈(-∞,0]时,≥0,所以不存在“10倍区间”,所以y=有1个“10倍区间”,为.
1
考点1 比较大小
1.(2021新高考Ⅱ,7)若a=log52,b=log83,c=,则( )
A.c
A.a
A. f >f()>f()
B. f >f()>f()
C. f()>f()>f
D. f()>f()>f
考点2 幂函数、指数函数、对数函数的图象
4.(2021天津,3)函数y=的图象大致为( )
5.(2020北京,6)已知函数f(x)=2x-x-1,则不等式f(x)>0的解集是( )
A.(-1,1)
B.(-∞,-1)∪(1,+∞)
C.(0,1)
D.(-∞,0)∪(1,+∞)
6.(2019课标全国Ⅲ,7)函数y=在[-6,6]上的图象大致为( )
7.(2018课标全国Ⅲ,7)下列函数中,其图象与函数y=ln x的图象关于直线x=1对称的是( )
A.y=ln(1-x) B.y=ln(2-x)
C.y=ln(1+x) D.y=ln(2+x)
8.(2018课标全国Ⅱ,3)函数f(x)=的图象大致为( )
A B C D
考点3 幂函数、指数函数、对数函数的性质
9.(2020全国Ⅰ理,12)若2a+log2a=4b+2log4b,则( )
A.a>2b B.a<2b C.a>b2 D.a
A.是奇函数,且在(0,+∞)单调递增
B.是奇函数,且在(0,+∞)单调递减
C.是偶函数,且在(0,+∞)单调递增
D.是偶函数,且在(0,+∞)单调递减
11.(2020全国Ⅱ理,9)设函数f(x)=ln|2x+1|-ln|2x-1|,则f(x)( )
A.是偶函数,且在单调递增
B.是奇函数,且在单调递减
C.是偶函数,且在单调递增
D.是奇函数,且在单调递减
12.(2021新高考Ⅰ,13)已知函数f(x)=x3(a·2x-2-x)是偶函数,则a= .
13.(2020北京,11)函数f(x)=+ln x的定义域是 .
14.(2020江苏,7)已知y=f(x)是奇函数,当x≥0时, f(x)=,则f(-8)的值是 .
考点4 反函数
(2020上海,4)已知函数f(x)=x3,f -1(x)是f(x)的反函数,则
f -1(x)= .
16.(2018上海,4)设常数a∈R,函数f(x)=log2(x+a).若f(x)的反函数的图象经过点(3,1),则a= .
应用实践
1.(2021江苏泰州期末)设函数f(x)=则满足不等式f(x)+f>2的x的取值范围是( )
A. B.
C. D.
2.(2021河南驻马店期末)设函数y=f(x)和y=f(-x),若两函数在区间[m,n]上的单调性相同,则把区间[m,n]叫作y=f(x)的“稳定区间”.已知区间[1,2 021]为函数g(x)=的“稳定区间”,则实数a的可能取值是( )
A.- B.- C. D.-4
3.(2021江苏南通如东高级中学期末)已知f(x)=若关于x的方程f(x)=m(m∈R)有四个不相等的实根x1,x2,x3,x4,则x1x2x3x4的取值范围是( )
A. B.
C. D.
4.(2022江苏马坝高级中学阶段检测)已知函数f(x)对于一切实数x,y均有f(x+y)-f(y)=x(x+2y+1)成立,且f(1)=0,则当x∈时,不等式f(x)+2
C.∪(1,+∞) D.
5.(多选)(2020山东菏泽期末)对数函数y=logax(a>0且a≠1)与二次函数y=(a-1)x2-x在同一坐标系内的图象不可能是( )
6.(多选)(2020江苏淮阴中学期末)已知函数f(x)=则方程[f(x)]2-2f(x)+a2-1=0的根的个数为( )
A.2 B.6 C.5 D.4
7.(2020江苏南通期末)已知函数f(x)=若f(x)在R上是增函数,则实数a的取值范围是 .
8.(2021河北唐山期末)已知定义域为R的函数f(x)=是奇函数.
(1)求y=f(x)的解析式;
(2)若f+f(4-2a)>0恒成立,求实数a的取值范围.
9.(2022上海杨浦期末)已知函数y=f(x)的定义域为D,若存在区间[a,b] D使得函数y=f(x)满足:
①函数y=f(x)在区间[a,b]上是严格增函数或严格减函数;
②函数y=f(x),x∈[a,b]的值域是[na,nb](n∈Z且n≥2).
则称区间[a,b]为函数y=f(x)的“n倍区间”.
(1)判断下列函数是否存在“2倍区间”(不需要说明理由);
①y=1-x;②y=x2+;
(2)证明:函数y=x-2不存在“n倍区间”;
(3)证明:当有理数m满足m∈(0,1)∪(1,+∞)时,对任意n(n∈Z且n≥2),函数y=xm都存在“n倍区间”,并求函数y=x3和y=所有的“10倍区间”.
答案全解全析
1.C 2.D 3.C 4.B 5.D 6.B 7.B 8.B
9.B 10.A 11.D
1.C ∵log52
∴b>c,∴a
∵0<0.40.3<0.40=1,∴0
∴f(-x)=f(x),∴f=f(-log34)=f(log34).
∵log34>log33=1,且1>>>0,
∴log34>>>0.
∵f(x)在(0,+∞)上单调递减,
∴f()>f(.故选C.
4.B 设f(x)=,则f(x)的定义域为{x|x≠0},
因为f(-x)=>0,排除D,故选B.
5.D 不等式f(x)>0等价于不等式2x>x+1,作出函数y=2x和函数y=x+1的图象,如图所示,易知两个函数图象的交点坐标为(1,2)和(0,1),观察函数图象可知,当x>1或x<0时,函数y=2x的图象在函数y=x+1图象的上方,此时2x>x+1,故不等式f(x)>0的解集为(-∞,0)∪(1,+∞),故选D.
6.B 设f(x)=(x∈[-6,6]),则f(-x)=≈7.97,排除选项A.故选B.
7.B 设所求函数图象上一点的坐标为(a,b),则点(a,b)关于直线x=1的对称点(2-a,b)在函数y=ln x的图象上,∴b=ln(2-a),故所求的函数为y=ln(2-x).
8.B 因为f(x)的定义域关于原点对称且f(-x)=-f(x),所以f(x)为奇函数,排除A选项;
f(2)=>1,排除C、D选项.故选B.
9.B 2a+log2a=22b+log2b<22b+log2(2b),令f(x)=2x+log2x,则f(a)
是奇函数,且在区间(0,+∞)上单调递增.故选A.
11.D x∈xx≠ ±,x∈R,∴函数f(x)的定义域关于原点对称,又∵f(-x)=ln|-2x+1|-ln|-2x-1|=ln|2x-1|-ln|2x+1|=-f(x),∴f(x)是奇函数,排除A、C;当x∈时,f(x)=ln(2x+1)-ln(1-2x),
∵y=ln(2x+1)在上单调递减,
∴f(x)在上单调递增,排除B;当x∈上单调递减,∴D正确.
12.答案 1
解析 ∵f(x)=x3(a·2x-2-x)为偶函数,
∴f(1)=f(-1),
∴2a-,∴a=1.
当a=1时,f(x)=x3(2x-2-x),定义域为R,且满足f(-x)=f(x),即f(x)为偶函数.
13.答案 (0,+∞)
解析 要使函数f(x)有意义,则故x>0,
因此函数f(x)的定义域为(0,+∞).
14.答案 -4
解析 由函数f(x)是奇函数得f(-8)=-f(8)=-=-4.
15.答案
解析 由f(x)=x3,得x=.
16.答案 7
解析 ∵f(x)的反函数的图象经过点(3,1),∴函数f(x)=log2(x+a)的图象经过点(1,3),
∴log2(1+a)=3,解得a=7.
1.D 2.B 3.D 4.D 5.BCD 6.ACD
1.D 当x-时,不等式显然成立;
当x≤1时,f(x)+f
综上,不等式的解集为.故选D.
2.B g(x)=,则g(-x)=|3x+a|.
①当两个函数都是增函数时,
在区间[1,2 021]上恒成立,即(-3x)max≤a≤,所以-3≤a≤-;
②当两个函数都是减函数时,在区间[1,2 021]上恒成立,即≤a≤(-3x)min,无解.综上,-3≤a≤-.
故选B.
3.D 画出函数f(x)的图象,如图所示:
由图可知,方程f(x)=m有四个不相等的实根时2≤m<.
设y=m与y=2-3x-2x2=-2(x≤0)图象的交点的横坐标从左到右为x1,x2,则x1<0,x2≤0,且x1+x2=-,x1x2≥0,
∴x1x2=(-x1)(-x2)<.
设y=m与y=|lg x|(x>0)图象的交点的横坐标从左到右为x3,x4,则x3>0,x4>0.
由|lg x3|=|lg x4|得lg x3=-lg x4,
∴x3x4=1.
∴x1x2x3x4∈.
故选D.
4.D 令x=1,y=0,则f(1)-f(0)=2,
∵f(1)=0,
∴f(0)=-2,
令y=0,则f(x)-f(0)=x(x+1),即f(x)=x2+x-2.
当x∈时,不等式f(x)+2
∴g(x)∈,
要使x2+x
当0
选项C,D中,由对数函数的图象得0
确定含参数的函数的图象,要分析函数中参数的几何意义.特别是二次函数中,要从图象的开口方向、对称轴、与x轴的交点位置等方面进行分析,对各个选项逐一进行判断
6.ACD 画出f(x)的图象,如图所示:
令t=f(x),则t2-2t+a2-1=0,Δ=4(2-a2).
当Δ=0,即a2=2时,t=1,此时f(x)=1,由图可知,直线y=1与y=f(x)的图象有2个交点,
所以方程[f(x)]2-2f(x)+a2-1=0的根的个数为2,A正确.
当Δ>0,即a2<2时,t=1±≤≤1+≤1-<1.
当t=1-时,f(x)∈[1-,1),由图可知x有2个解;
当t=1+时,若t∈(1,2],则x有3个解;若t∈(2,1+],则x有2个解.
故方程[f(x)]2-2f(x)+a2-1=0的根的个数为5或4,C、D正确.故选ACD.
7.答案
解析 因为函数f(x)在R上是增函数,
所以y=(3-a)x+a-1在区间(-∞,1)上是增函数且y=loga在区间[1,+∞)上也是增函数.
由函数y=(3-a)x+a-1在(-∞,1)上是增函数,得3-a>0 a<3.①
对于函数y=loga,x∈[1,+∞),令u=x2-ax+=.
当0
所以根据复合函数“同增异减”可得0
所以解得a≤2,
又a>1,所以1
loga,
即a2+a-≤0,解得-≤a≤.
所以实数a的取值范围是.
8.解析 (1)因为函数f(x)=为奇函数,
所以f(-x)=-f(x),
即,
所以,
所以n·3x-1=-n+3x,
即(n-1)(3x+1)=0,解得n=1.
故函数f(x)=.
(2)由(1)知f(x)=·,
所以f(x)在(-∞,+∞)上单调递减.
由f>-f(4-2a).
因为函数f(x)是奇函数,
所以f>f(2a-4),
所以log4x·(3-log2x)<2a-4,
整理得log2x·(3-log2x)<2a-4.
设t=log2x,t∈R,则(3t-t2)<2a-4恒成立,
令y=.
9.解析 (1)y=1-x不存在“2倍区间”,y=x2+存在“2倍区间”.
理由如下:根据严格单调定义可知,函数y=1-x在R上严格单调递减,若[a,b]是函数的2倍区间,则函数的值域为[1-b,1-a],且,不满足a
∴
即函数y=x2+.
(2)证明:假设存在区间[a,b]是y=x-2的“n倍区间”(n∈Z,且n≥2),
由条件①可知,[a,b] (-∞,0)或[a,b] (0,+∞).当[a,b] (0,+∞),即0
所以
所以=1,即a=b,
这与a
当[a,b] (-∞,0)时,[na,nb] (-∞,0),
这与x∈(-∞,0)时,y=x-2>0矛盾,
即y=x-2在x∈(-∞,0)上不存在“n倍区间”.
综上所述,函数y=x-2不存在“n倍区间”.
(3)先考虑y=xm,x∈[0,+∞)的情况,
因为y=xm在[0,+∞)上是严格增函数,所以若存在“n倍区间”,则xm=nx有两个非负解,方程xm=nx可化为x(xm-1-n)=0,
当m∈(0,1)∪(1,+∞)时,方程xm=nx有两个非负解x=0和x=,
所以至少存在一个“n倍区间”为[0,].
y=x3在(-∞,+∞)是严格增函数,
令x3=10x,解得x1=0,x2=,
所以y=x3有三个“10倍区间”,分别是[-].
y=在[0,+∞)上是严格增函数,在(-∞,0]上是严格减函数,
当x∈(-∞,0]时,≥0,所以不存在“10倍区间”,所以y=有1个“10倍区间”,为.
1
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
