苏教版(2019)高中数学必修一7.2.3 三角函数的诱导公式同步练习(Word含答案)
文档属性
| 名称 | 苏教版(2019)高中数学必修一7.2.3 三角函数的诱导公式同步练习(Word含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 45.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-06 15:52:50 | ||
图片预览



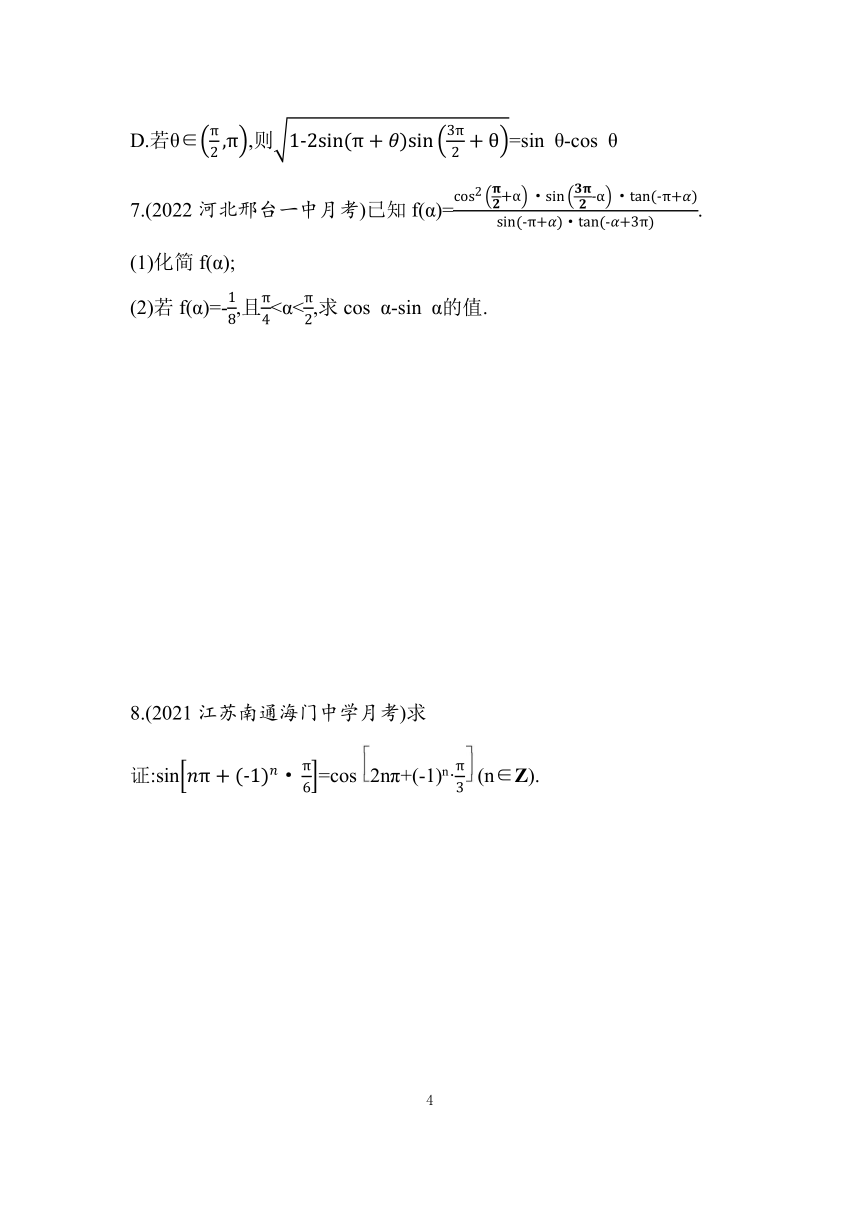
文档简介
7.2.3 三角函数的诱导公式
基础过关练
题组一 利用诱导公式解决给角求值问题
1.(2022江苏宿迁期末)已知角α的终边经过点P(-2,1),则cos的值为( )
A. B. C.- D.-
2.(2021江苏无锡锡山高级中学期末)若角α的顶点在原点,始边在x轴非负半轴上,终边上一点P的坐标为,则角α为( )
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
3.(2021山东潍坊一中月考)sin(-1 200°)·tan(-30°)-cos 585°·
tan(-1 665°)= .
题组二 利用诱导公式解决给值求值问题
(2021山东枣庄三中质检)已知sin(α+3π)=-,且α为第二象限角,则
cos α=( )
A.- B. C.- D.-
5.(2021江苏连云港海州高级中学月考)已知tan=,则
tan=( )
A. B.- C. D.-
6.(2022江苏盐城时杨中学期中)已知cos(α-π)=-,且α是第四象限角,则sin α=( )
A.- B. C. D.±
7.(2022广东深圳期末)已知sin=-,则cos=( )
A. B.- C. D.-
8.(2022江苏南通海安高级中学期中)当θ∈时,若cos=-,则sin的值为( )
A. B. C.± D.-
题组三 利用诱导公式化简、证明恒等式
9.化简sincostan的结果是( )
A.1 B.sin2α C.-cos2α D.-1
10.(2022天津耀华中学期末)已知角A、B、C为△ABC的三个内角,若sin=sin,则△ABC一定是( )
A.等腰直角三角形
B.直角三角形
C.等腰三角形
D.等腰三角形或直角三角形
11.(2021江苏连云港赣榆第一中学月考)求证:=-tan θ.
能力提升练
题组一 利用诱导公式解决求值问题
1.(2021广东中山纪念中学期中)若cos=,则cos-sin2=( )
A.- B.-
C.- D.
2.(2021江苏常州第二中学月考)已知3sin+α=-5cos,则tan=( )
A.- B.-
C. D.
3.(2022湖南长沙月考)已知α为锐角,若sin=,则sin= .
4.若sin θ=,则+= .
5.(2020河南郑州期末)已知sin=-,则sin2-sin的值为 .
题组二 利用诱导公式化简、证明恒等式
6.(多选)下列化简正确的是( )
A.=cos α
B.=tan α
C.=1
D.若θ∈,则=sin θ-cos θ
7.(2022河北邢台一中月考)已知f(α)=.
(1)化简f(α);
(2)若f(α)=-,且<α<,求cos α-sin α的值.
8.(2021江苏南通海门中学月考)求证:sin=cos2nπ+(-1)n·(n∈Z).
答案全解全析
基础过关练
1.A 2.C 4.D 5.B 6.A 7.D 8.B 9.C
10.C
1.A 由题意可得|OP|=(O为坐标原点),
∴sin α=,
∴cos.故选A.
2.C sin<0,
所以点P在第三象限,所以角α为第三象限角.故选C.
3.答案
解析 sin(-1 200°)·tan(-30°)-cos 585°·tan(-1 665°)=-sin(3×360°+120°)·-cos(720°-135°)·tan(-9×180°-45°)=sin 120°-
cos 135°·tan(-45°)=.
4.D ∵sin(α+3π)=-sin α=-,
∴sin α=.
∵sin2α+cos2α=1,
∴,
又α为第二象限角,∴cos α=-.故选D.
5.B ∵tan.故选B.
6.A ∵cos(α-π)=cos(π-α)=-cos α=-
.
7.D ∵sin.故选D.
8.B ∵θ∈-θ∈,
∴sin,
∴sin.
9.C 因为sin=cos α,
cos=-sin α,
tan,
所以原式=cos α·(-sin α)·=-cos2α.故选C.
10.C 因为sin,
所以sin,
即sin,即cos C=cos B,即B=C,故该三角形一定是等腰三角形.故选C.
11.证明 因为左边==-tan θ=右边,
所以原等式成立.
能力提升练
1.A 2.C 6.AD
1.A cos
=cos
=-cos
=-.故选A.
2.C 由诱导公式可知3sin,
又3sin,
所以-3sin,
所以tan,
所以tan.
故选C.
3.答案 -
解析 因为α为锐角,所以0<α<.
4.答案 6
解析 原式==6.
5.答案
解析 设,
所以sin2-sin(π-θ)=cos2θ-sin θ=1-sin2θ-sin θ=1-.
6.AD A正确,=cos α;
B错误,=-tan α;
C错误,
==-1;
D正确,
=
=
=|sin θ-cos θ|,
∵θ∈=sin θ-cos θ.故选AD.
7.解析 (1)由题知,f(α)==-sin αcos α.
(2)由(1)知,f(α)=-sin αcos α,∵f(α)=-,
∴sin αcos α=,∴(cos α-sin α)2=cos2α-2sin α·cos α+sin2α=1-2sin αcos α=1-2×,
又∵,∴cos α∴cos α-sin α=-.
8.证明 ①当n=2k,k∈Z时,
左边=sin,
右边=cos,
左边=右边,则原等式成立;
②当n=2k+1,k∈Z时,
左边=sin
=sin,
右边=cos2(2k+1)π+(-1)2k+1·
=cos,
左边=右边,则原等式成立.
综上,sin=cos2nπ+(-1)n·(n∈Z).
1
基础过关练
题组一 利用诱导公式解决给角求值问题
1.(2022江苏宿迁期末)已知角α的终边经过点P(-2,1),则cos的值为( )
A. B. C.- D.-
2.(2021江苏无锡锡山高级中学期末)若角α的顶点在原点,始边在x轴非负半轴上,终边上一点P的坐标为,则角α为( )
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
3.(2021山东潍坊一中月考)sin(-1 200°)·tan(-30°)-cos 585°·
tan(-1 665°)= .
题组二 利用诱导公式解决给值求值问题
(2021山东枣庄三中质检)已知sin(α+3π)=-,且α为第二象限角,则
cos α=( )
A.- B. C.- D.-
5.(2021江苏连云港海州高级中学月考)已知tan=,则
tan=( )
A. B.- C. D.-
6.(2022江苏盐城时杨中学期中)已知cos(α-π)=-,且α是第四象限角,则sin α=( )
A.- B. C. D.±
7.(2022广东深圳期末)已知sin=-,则cos=( )
A. B.- C. D.-
8.(2022江苏南通海安高级中学期中)当θ∈时,若cos=-,则sin的值为( )
A. B. C.± D.-
题组三 利用诱导公式化简、证明恒等式
9.化简sincostan的结果是( )
A.1 B.sin2α C.-cos2α D.-1
10.(2022天津耀华中学期末)已知角A、B、C为△ABC的三个内角,若sin=sin,则△ABC一定是( )
A.等腰直角三角形
B.直角三角形
C.等腰三角形
D.等腰三角形或直角三角形
11.(2021江苏连云港赣榆第一中学月考)求证:=-tan θ.
能力提升练
题组一 利用诱导公式解决求值问题
1.(2021广东中山纪念中学期中)若cos=,则cos-sin2=( )
A.- B.-
C.- D.
2.(2021江苏常州第二中学月考)已知3sin+α=-5cos,则tan=( )
A.- B.-
C. D.
3.(2022湖南长沙月考)已知α为锐角,若sin=,则sin= .
4.若sin θ=,则+= .
5.(2020河南郑州期末)已知sin=-,则sin2-sin的值为 .
题组二 利用诱导公式化简、证明恒等式
6.(多选)下列化简正确的是( )
A.=cos α
B.=tan α
C.=1
D.若θ∈,则=sin θ-cos θ
7.(2022河北邢台一中月考)已知f(α)=.
(1)化简f(α);
(2)若f(α)=-,且<α<,求cos α-sin α的值.
8.(2021江苏南通海门中学月考)求证:sin=cos2nπ+(-1)n·(n∈Z).
答案全解全析
基础过关练
1.A 2.C 4.D 5.B 6.A 7.D 8.B 9.C
10.C
1.A 由题意可得|OP|=(O为坐标原点),
∴sin α=,
∴cos.故选A.
2.C sin<0,
所以点P在第三象限,所以角α为第三象限角.故选C.
3.答案
解析 sin(-1 200°)·tan(-30°)-cos 585°·tan(-1 665°)=-sin(3×360°+120°)·-cos(720°-135°)·tan(-9×180°-45°)=sin 120°-
cos 135°·tan(-45°)=.
4.D ∵sin(α+3π)=-sin α=-,
∴sin α=.
∵sin2α+cos2α=1,
∴,
又α为第二象限角,∴cos α=-.故选D.
5.B ∵tan.故选B.
6.A ∵cos(α-π)=cos(π-α)=-cos α=-
.
7.D ∵sin.故选D.
8.B ∵θ∈-θ∈,
∴sin,
∴sin.
9.C 因为sin=cos α,
cos=-sin α,
tan,
所以原式=cos α·(-sin α)·=-cos2α.故选C.
10.C 因为sin,
所以sin,
即sin,即cos C=cos B,即B=C,故该三角形一定是等腰三角形.故选C.
11.证明 因为左边==-tan θ=右边,
所以原等式成立.
能力提升练
1.A 2.C 6.AD
1.A cos
=cos
=-cos
=-.故选A.
2.C 由诱导公式可知3sin,
又3sin,
所以-3sin,
所以tan,
所以tan.
故选C.
3.答案 -
解析 因为α为锐角,所以0<α<.
4.答案 6
解析 原式==6.
5.答案
解析 设,
所以sin2-sin(π-θ)=cos2θ-sin θ=1-sin2θ-sin θ=1-.
6.AD A正确,=cos α;
B错误,=-tan α;
C错误,
==-1;
D正确,
=
=
=|sin θ-cos θ|,
∵θ∈=sin θ-cos θ.故选AD.
7.解析 (1)由题知,f(α)==-sin αcos α.
(2)由(1)知,f(α)=-sin αcos α,∵f(α)=-,
∴sin αcos α=,∴(cos α-sin α)2=cos2α-2sin α·cos α+sin2α=1-2sin αcos α=1-2×,
又∵,∴cos α
8.证明 ①当n=2k,k∈Z时,
左边=sin,
右边=cos,
左边=右边,则原等式成立;
②当n=2k+1,k∈Z时,
左边=sin
=sin,
右边=cos2(2k+1)π+(-1)2k+1·
=cos,
左边=右边,则原等式成立.
综上,sin=cos2nπ+(-1)n·(n∈Z).
1
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
