苏教版(2019)高中数学必修一8.1.1 函数的零点同步练习(Word含答案)
文档属性
| 名称 | 苏教版(2019)高中数学必修一8.1.1 函数的零点同步练习(Word含答案) | 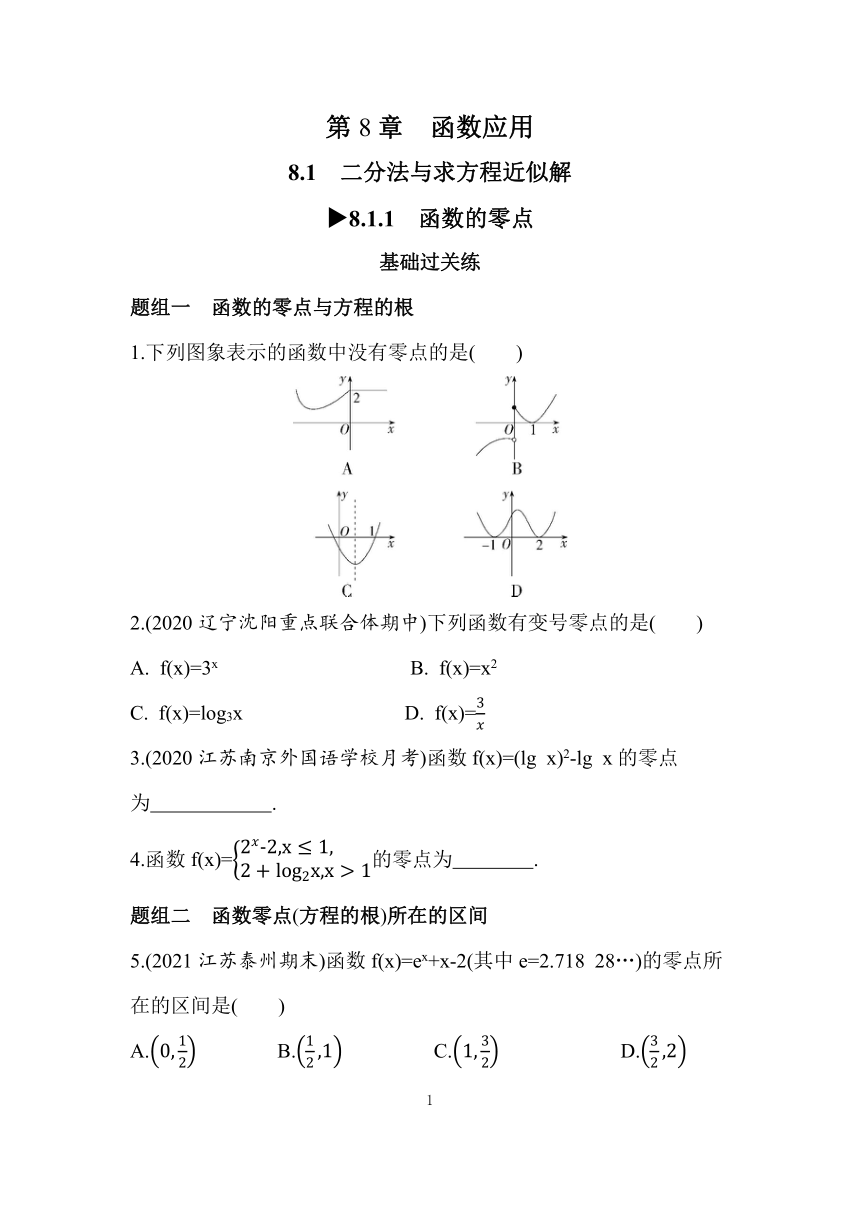 | |
| 格式 | docx | ||
| 文件大小 | 288.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-06 15:58:40 | ||
图片预览





文档简介
第8章 函数应用
8.1 二分法与求方程近似解
8.1.1 函数的零点
基础过关练
题组一 函数的零点与方程的根
1.下列图象表示的函数中没有零点的是( )
2.(2020辽宁沈阳重点联合体期中)下列函数有变号零点的是( )
A. f(x)=3x B. f(x)=x2
C. f(x)=log3x D. f(x)=
3.(2020江苏南京外国语学校月考)函数f(x)=(lg x)2-lg x的零点为 .
4.函数f(x)=的零点为 .
题组二 函数零点(方程的根)所在的区间
5.(2021江苏泰州期末)函数f(x)=ex+x-2(其中e=2.718 28…)的零点所在的区间是( )
A. B. C. D.
6.(2021江苏宿迁期末)函数f(x)=lg(2x)+x-1的零点所在区间为( )
A. B.
C. D.
7.(2021江苏无锡锡山高级中学期末)设x∈R,用[x]表示不超过x的最大整数,y=[x]被称为“高斯函数”,例如[2.1]=2,[3]=3,[-1.5]=-2.设x0为函数f(x)=log2x--1的零点,则[x0]=( )
A.2 B.3
C.4 D.5
题组三 确定函数的零点个数
8.已知函数f(x)的图象是连续不断的,有如下x, f(x)的对应值表:
x 1 2 3 4 5 6
f(x) 15 10 -7 6 -4 -5
则函数f(x)在区间[1,6]上的零点至少有( )
A.2个 B.3个
C.4个 D.5个
9.(2022江苏苏州实验中学期中)函数f(x)=的零点个数为( )
A.2 B.3
C.4 D.5
10.(2022江苏东台第一中学期中)已知函数f(x)=函数g(x)=3-f(2-x),则函数y=f(x)-g(x)的零点个数为 .
11.判断函数f(x)=ln x+x2-3的零点个数.
题组四 根据函数零点(方程根)的情况求参数的值或范围
12.(多选)(2021江苏扬州期末)设函数f(x)=若函数g(x)=f(x)-m有四个零点,则实数m的值可以是( )
A.-1 B.1 C.3 D.5
13.(2022江苏马塘中学期中)已知函数f(x)=若方程[f(x)]2-4mf(x)+m2+2=0有四个不相等的实数根,则实数m的取值范围为 .
14.已知函数f(x)=x2-bx+3.
(1)若f(0)=f(4),求函数f(x)的零点;
(2)若函数f(x)的一个零点大于1,另一个零点小于1,求实数b的取值
范围.
15.(2021江苏苏州实验中学月考)已知函数f(x)=.
(1)若f(x)为偶函数,求a的值;
(2)若函数g(x)=f(x)-(a+1)在[-1,1]上有2个不同的零点,求实数a的取值范围.
能力提升练
题组一 函数零点的个数及零点的应用
1.(2021江苏淮安期末)函数f(x)=x+x3,g(x)=x+3x,h(x)=x+log3x的零点分别是a,b,c,则它们的大小关系为( )
A.a>b>c B.a>c>b
C.c>a>b D.c>b>a
2.(2021安徽合肥十中期末)已知函数f(x)=3-4||x-1|-1|,则函数y=f(x)-lg|x|的零点个数为( )
A.2 B.3 C.4 D.5
3.(2022江苏常州高级中学期末)函数f(x)=sin x-的零点个数是( )
A.8 B.9 C.10 D.11
题组二 根据函数零点(方程根)的情况求参数的值或范围
4.若函数f(x)=(2ax-1)2-loga(ax+2)在区间上恰有一个零点,则实数a的取值范围是( )
A. B.[3,+∞)
C.[2,3] D.[2,3)
5.(多选)(2022江苏常州高级中学期中)已知函数f(x)=若函数g(x)=f[2f(x)]+a有7个零点,则实数a的可能取值是( )
A.0 B.- C.- D.-
6.(2022江苏宿迁中学期中)已知函数f(x)=(a>0且a≠1)在R上单调递减,且关于x的方程f(x)=2-恰有两个不相等的实数解,则a的取值范围是 .
7.(2022江苏白塔高级中学期中)已知f(x)是定义在(-∞,0)∪(0,+∞)上的奇函数,且当x>0时,f(x)=g(x)=f(x)-a.
(1)若函数g(x)恰有三个不同的零点,求实数a的值;
(2)记h(a)为函数g(x)的所有零点之和.当-18.(2021江苏丹阳高级中学期末)已知函数f(x)=lg(m为常数且m<0)为奇函数.
(1)求m的值;
(2)设函数g(x)=f(x)-lg(4x+a-4),若函数g(x)有零点,求实数a的取值
范围.
答案全解全析
基础过关练
1.A 2.C 5.A 6.B 7.B 8.B 9.A 12.BC
1.A
2.C 对于A,函数f(x)=3x>0,不存在零点,故A不符合题意;对于B,函数f(x)=x2存在零点x=0,但当x<0时,f(x)>0,当x>0时,f(x)>0,不是变号零点,故B不符合题意;对于C,函数f(x)=log3x存在零点x=1,且当01时,f(x)>0,故C符合题意;对于D,函数f(x)=不存在零点,故D不符合题意.故选C.
3.答案 1,10
解析 令(lg x)2-lg x=0,得lg x(lg x-1)=0,∴lg x=0或lg x=1,∴x=1或x=10.
4.答案 1
解析 当x≤1时,令2x-2=0,解得x=1;当x>1时,令2+log2x=0,解得x=(舍去),所以函数f(x)存在零点,且零点为1.
5.A 易知函数f(x)为R上的增函数,且图象是不间断的.因为f(0)=-1<0,f.故选A.
6.B 易知f(x)在(0,+∞)上单调递增,且图象是不间断的.因为f·f(1)<0,所以由函数零点存在定理可知函数f(x)的零点所在区间为.故选B.
7.B 易知f(x)=log2x->0,所以由函数零点存在定理可知x0∈(3,4),所以[x0]=3.
故选B.
8.B 由题表可知f(2)f(3)<0,f(3)f(4)<0,f(4)f(5)<0,又f(x)的图象是连续不断的,故函数f(x)在区间[1,6]上至少有3个零点.
9.A 令f(x)=0,则
解得x=0或x=1,所以函数的零点个数为2.
故选A.
10.答案 2
解析 由题意知y=f(x)+f(2-x)-3.
因为f(x)=,
所以f(x)+f(2-x)=
在同一平面直角坐标系中分别画出函数y=f(x)+f(2-x)的图象与直线y=3,如图所示:
由图可知,函数y=f(x)+f(2-x)的图象与直线y=3有2个交点,故函数y=f(x)-g(x)只有2个零点.
11.解析 解法一:函数对应的方程为ln x+x2-3=0,故原函数的零点个数即为函数y=ln x与y=3-x2的图象交点个数.
在同一平面直角坐标系中,作出函数y=ln x和y=3-x2的图象,如图所示:
由图象知,函数y=3-x2与y=ln x的图象只有一个交点,从而ln x+x2-3=0只有一个根,即函数f(x)=ln x+x2-3有一个零点.
解法二:∵f(1)=ln 1+12-3=-2<0,
f(2)=ln 2+22-3=ln 2+1>0,
∴f(1)·f(2)<0,
又f(x)=ln x+x2-3的图象在(1,2)上是不间断的,∴f(x)在(1,2)上必有零点,
又f(x)在(0,+∞)上是单调递增的,
∴函数的零点有且只有一个.
12.BC 函数g(x)=f(x)-m有四个零点等价于y=f(x)的图象与直线y=m有四个不同的交点.
作出f(x)的图象如图所示:
由图知,若y=f(x)的图象与直线y=m有四个不同的交点,则m∈(0,4),故选BC.
13.答案 ∪(3,+∞)
解析 令t=f(x),则方程[f(x)]2-4mf(x)+m2+2=0转化为t2-4mt+m2+2=0,
作出函数f(x)的图象如图所示,
由题意,方程[f(x)]2-4mf(x)+m2+2=0有四个不相等的实数根,即t2-4mt+m2+2=0有两个大于1的不等实数根,
令h(t)=t2-4mt+m2+2,则则实数m的取值范围为∪(3,+∞).
14.解析 (1)因为f(0)=f(4),所以3=16-4b+3,解得b=4,所以f(x)=x2-4x+3.
令f(x)=0,即x2-4x+3=0,解得x1=3,x2=1,所以函数f(x)的零点是1和3.
(2)要使函数f(x)的一个零点大于1,另一个零点小于1,需满足解得b>4.故实数b的取值范围为(4,+∞).
15.解析 (1)因为函数f(x)为偶函数,所以f(-x)=f(x),即,
整理得(a-1)(4x-1)=0,所以a=1.
(2)g(x)=f(x)-(a+1)=-(a+1).
令g(x)=0,可得-(a+1)=0,整理得4x-(a+1)·2x+a=0,即(2x-a)(2x-1)=0.
因为函数g(x)在[-1,1]上有2个不同的零点,
所以x=0或x=log2a(a>0),且-1≤log2a≤1,log2a≠0,解得≤a<1或1所以实数a的取值范围为∪(1,2].
能力提升练
1.C 2.C 3.D 4.D 5.BD
1.C f(x)=x+x3,g(x)=x+3x,h(x)=x+log3x的零点分别为y=x3,y=3x,y=log3x的图象与y=-x的图象的交点的横坐标.在同一平面直角坐标系中作出y=x3,y=3x,y=log3x,y=-x的图象,如图.
由图可知c>a>b.故选C.
2.C 易得f(x)=
函数y=f(x)-lg|x|的零点个数即为y=f(x)与y=g(x)=lg|x|图象的交点个数.
在同一平面直角坐标系中作出函数y=f(x)与y=g(x)=lg|x|的大致图象如图所示.
由图可知,函数y=f(x)-lg|x|的零点有4个,故选C.
3.D 在同一平面直角坐标系中,作出y=sin x与y=的图象,如图.
由图可知,当x≥5π时,>1>sin x,所以此时两函数图象无交点;
当0由对称性知,当-5π当x=0时,两函数图象有1个交点.
所以函数f(x)的零点个数为5+5+1=11.
4.D 函数f(x)在区间≤0,即(1-loga2)·(1-loga3)≤0,
则
解得2≤a≤3,
当a=3时,f(x)=(6x-1)2-log3(3x+2),
显然函数f(x)在区间上有两个零点,不符合
题意.
经检验,当a=2时,符合题意.
故实数a的取值范围为[2,3).故选D.
5.BD 由题知,f(x)在x∈(-∞,0]上单调递增,其值域为(-∞,1];
f(x)在(0,1]上单调递减,其值域为[0,+∞);
f(x)在(1,+∞)上单调递增,其值域为(0,+∞).
作出y=f(x)的图象,如图所示:
∵g(x)=f[2f(x)]+a有7个零点,即f[2f(x)]=-a有7个不同的解,
当-a<0时,有2f(x)<-1,即f(x)<-,此时g(x)有1个零点;
当-a=0时,有2f(x)=±1,即f(x)=±,
∴f(x)=-有3个解,
此时g(x)共有4个零点;
当0<-a≤lg 2时,有-1<2f(x)≤lg 2-1或≤2f(x)<1或1<2f(x)≤2,
∴-当lg 2<-a≤1时,有lg 2-1<2f(x)≤0或0<2f(x)<或2<2f(x)≤10,
∴此时g(x)共有6个零点;
当-a>1时,有0<2f(x)<或2f(x)>10,
∴05有2个零点,此时g(x)共有5个零点.
综上,要使g(x)有7个零点,则-lg 2≤a<0.
结合选项知,a的可能取值是-.
故选BD.
6.答案
解析 由题意得≤a≤,
作出函数y=f(x)与y=2-的图象,如图所示:
若f(x)=2-,故a∈.
7.解析 (1)根据题意画出函数f(x)的图象,如图所示:
由图象可知,当且仅当a=2或a=-2时,直线y=a与函数y=f(x)的图象有三个不同的交点,即函数g(x)恰有三个不同的零点,故a=2或a=-2.
(2)由(1)中f(x)的图象可知,当-1∴h(a)=-10-log3(7-a)+log3(7+a)+10=log3,
当-1∴h(a)∈(1-2log32,2log32-1),
故当-18.解析 (1)因为函数f(x)为奇函数,所以f(-x)=-f(x),即f(-x)+f(x)=0,
又f(x)=lg,
f(-x)=lg,
所以lg=0,
即lg=0,
所以=1,
所以(m+1)2=1,
又m<0,所以m=-2.
(2)由(1)可得f(x)=lg.
令-1+>0,得-1所以函数f(x)的定义域为(-1,1).
函数g(x)=f(x)-lg(4x+a-4)有零点,即g(x)=0有实数根,
即lg与y=4x+a-4=4(x-1)+a的图象在(-1,1)上有交点.画出两个函数在(-1,1)上的大致图象,如图所示.
易知y=4(x-1)+a过定点(1,a),且斜率为4,所以由图可知a>0.
1
8.1 二分法与求方程近似解
8.1.1 函数的零点
基础过关练
题组一 函数的零点与方程的根
1.下列图象表示的函数中没有零点的是( )
2.(2020辽宁沈阳重点联合体期中)下列函数有变号零点的是( )
A. f(x)=3x B. f(x)=x2
C. f(x)=log3x D. f(x)=
3.(2020江苏南京外国语学校月考)函数f(x)=(lg x)2-lg x的零点为 .
4.函数f(x)=的零点为 .
题组二 函数零点(方程的根)所在的区间
5.(2021江苏泰州期末)函数f(x)=ex+x-2(其中e=2.718 28…)的零点所在的区间是( )
A. B. C. D.
6.(2021江苏宿迁期末)函数f(x)=lg(2x)+x-1的零点所在区间为( )
A. B.
C. D.
7.(2021江苏无锡锡山高级中学期末)设x∈R,用[x]表示不超过x的最大整数,y=[x]被称为“高斯函数”,例如[2.1]=2,[3]=3,[-1.5]=-2.设x0为函数f(x)=log2x--1的零点,则[x0]=( )
A.2 B.3
C.4 D.5
题组三 确定函数的零点个数
8.已知函数f(x)的图象是连续不断的,有如下x, f(x)的对应值表:
x 1 2 3 4 5 6
f(x) 15 10 -7 6 -4 -5
则函数f(x)在区间[1,6]上的零点至少有( )
A.2个 B.3个
C.4个 D.5个
9.(2022江苏苏州实验中学期中)函数f(x)=的零点个数为( )
A.2 B.3
C.4 D.5
10.(2022江苏东台第一中学期中)已知函数f(x)=函数g(x)=3-f(2-x),则函数y=f(x)-g(x)的零点个数为 .
11.判断函数f(x)=ln x+x2-3的零点个数.
题组四 根据函数零点(方程根)的情况求参数的值或范围
12.(多选)(2021江苏扬州期末)设函数f(x)=若函数g(x)=f(x)-m有四个零点,则实数m的值可以是( )
A.-1 B.1 C.3 D.5
13.(2022江苏马塘中学期中)已知函数f(x)=若方程[f(x)]2-4mf(x)+m2+2=0有四个不相等的实数根,则实数m的取值范围为 .
14.已知函数f(x)=x2-bx+3.
(1)若f(0)=f(4),求函数f(x)的零点;
(2)若函数f(x)的一个零点大于1,另一个零点小于1,求实数b的取值
范围.
15.(2021江苏苏州实验中学月考)已知函数f(x)=.
(1)若f(x)为偶函数,求a的值;
(2)若函数g(x)=f(x)-(a+1)在[-1,1]上有2个不同的零点,求实数a的取值范围.
能力提升练
题组一 函数零点的个数及零点的应用
1.(2021江苏淮安期末)函数f(x)=x+x3,g(x)=x+3x,h(x)=x+log3x的零点分别是a,b,c,则它们的大小关系为( )
A.a>b>c B.a>c>b
C.c>a>b D.c>b>a
2.(2021安徽合肥十中期末)已知函数f(x)=3-4||x-1|-1|,则函数y=f(x)-lg|x|的零点个数为( )
A.2 B.3 C.4 D.5
3.(2022江苏常州高级中学期末)函数f(x)=sin x-的零点个数是( )
A.8 B.9 C.10 D.11
题组二 根据函数零点(方程根)的情况求参数的值或范围
4.若函数f(x)=(2ax-1)2-loga(ax+2)在区间上恰有一个零点,则实数a的取值范围是( )
A. B.[3,+∞)
C.[2,3] D.[2,3)
5.(多选)(2022江苏常州高级中学期中)已知函数f(x)=若函数g(x)=f[2f(x)]+a有7个零点,则实数a的可能取值是( )
A.0 B.- C.- D.-
6.(2022江苏宿迁中学期中)已知函数f(x)=(a>0且a≠1)在R上单调递减,且关于x的方程f(x)=2-恰有两个不相等的实数解,则a的取值范围是 .
7.(2022江苏白塔高级中学期中)已知f(x)是定义在(-∞,0)∪(0,+∞)上的奇函数,且当x>0时,f(x)=g(x)=f(x)-a.
(1)若函数g(x)恰有三个不同的零点,求实数a的值;
(2)记h(a)为函数g(x)的所有零点之和.当-1
(1)求m的值;
(2)设函数g(x)=f(x)-lg(4x+a-4),若函数g(x)有零点,求实数a的取值
范围.
答案全解全析
基础过关练
1.A 2.C 5.A 6.B 7.B 8.B 9.A 12.BC
1.A
2.C 对于A,函数f(x)=3x>0,不存在零点,故A不符合题意;对于B,函数f(x)=x2存在零点x=0,但当x<0时,f(x)>0,当x>0时,f(x)>0,不是变号零点,故B不符合题意;对于C,函数f(x)=log3x存在零点x=1,且当0
3.答案 1,10
解析 令(lg x)2-lg x=0,得lg x(lg x-1)=0,∴lg x=0或lg x=1,∴x=1或x=10.
4.答案 1
解析 当x≤1时,令2x-2=0,解得x=1;当x>1时,令2+log2x=0,解得x=(舍去),所以函数f(x)存在零点,且零点为1.
5.A 易知函数f(x)为R上的增函数,且图象是不间断的.因为f(0)=-1<0,f.故选A.
6.B 易知f(x)在(0,+∞)上单调递增,且图象是不间断的.因为f·f(1)<0,所以由函数零点存在定理可知函数f(x)的零点所在区间为.故选B.
7.B 易知f(x)=log2x->0,所以由函数零点存在定理可知x0∈(3,4),所以[x0]=3.
故选B.
8.B 由题表可知f(2)f(3)<0,f(3)f(4)<0,f(4)f(5)<0,又f(x)的图象是连续不断的,故函数f(x)在区间[1,6]上至少有3个零点.
9.A 令f(x)=0,则
解得x=0或x=1,所以函数的零点个数为2.
故选A.
10.答案 2
解析 由题意知y=f(x)+f(2-x)-3.
因为f(x)=,
所以f(x)+f(2-x)=
在同一平面直角坐标系中分别画出函数y=f(x)+f(2-x)的图象与直线y=3,如图所示:
由图可知,函数y=f(x)+f(2-x)的图象与直线y=3有2个交点,故函数y=f(x)-g(x)只有2个零点.
11.解析 解法一:函数对应的方程为ln x+x2-3=0,故原函数的零点个数即为函数y=ln x与y=3-x2的图象交点个数.
在同一平面直角坐标系中,作出函数y=ln x和y=3-x2的图象,如图所示:
由图象知,函数y=3-x2与y=ln x的图象只有一个交点,从而ln x+x2-3=0只有一个根,即函数f(x)=ln x+x2-3有一个零点.
解法二:∵f(1)=ln 1+12-3=-2<0,
f(2)=ln 2+22-3=ln 2+1>0,
∴f(1)·f(2)<0,
又f(x)=ln x+x2-3的图象在(1,2)上是不间断的,∴f(x)在(1,2)上必有零点,
又f(x)在(0,+∞)上是单调递增的,
∴函数的零点有且只有一个.
12.BC 函数g(x)=f(x)-m有四个零点等价于y=f(x)的图象与直线y=m有四个不同的交点.
作出f(x)的图象如图所示:
由图知,若y=f(x)的图象与直线y=m有四个不同的交点,则m∈(0,4),故选BC.
13.答案 ∪(3,+∞)
解析 令t=f(x),则方程[f(x)]2-4mf(x)+m2+2=0转化为t2-4mt+m2+2=0,
作出函数f(x)的图象如图所示,
由题意,方程[f(x)]2-4mf(x)+m2+2=0有四个不相等的实数根,即t2-4mt+m2+2=0有两个大于1的不等实数根,
令h(t)=t2-4mt+m2+2,则
14.解析 (1)因为f(0)=f(4),所以3=16-4b+3,解得b=4,所以f(x)=x2-4x+3.
令f(x)=0,即x2-4x+3=0,解得x1=3,x2=1,所以函数f(x)的零点是1和3.
(2)要使函数f(x)的一个零点大于1,另一个零点小于1,需满足解得b>4.故实数b的取值范围为(4,+∞).
15.解析 (1)因为函数f(x)为偶函数,所以f(-x)=f(x),即,
整理得(a-1)(4x-1)=0,所以a=1.
(2)g(x)=f(x)-(a+1)=-(a+1).
令g(x)=0,可得-(a+1)=0,整理得4x-(a+1)·2x+a=0,即(2x-a)(2x-1)=0.
因为函数g(x)在[-1,1]上有2个不同的零点,
所以x=0或x=log2a(a>0),且-1≤log2a≤1,log2a≠0,解得≤a<1或1
能力提升练
1.C 2.C 3.D 4.D 5.BD
1.C f(x)=x+x3,g(x)=x+3x,h(x)=x+log3x的零点分别为y=x3,y=3x,y=log3x的图象与y=-x的图象的交点的横坐标.在同一平面直角坐标系中作出y=x3,y=3x,y=log3x,y=-x的图象,如图.
由图可知c>a>b.故选C.
2.C 易得f(x)=
函数y=f(x)-lg|x|的零点个数即为y=f(x)与y=g(x)=lg|x|图象的交点个数.
在同一平面直角坐标系中作出函数y=f(x)与y=g(x)=lg|x|的大致图象如图所示.
由图可知,函数y=f(x)-lg|x|的零点有4个,故选C.
3.D 在同一平面直角坐标系中,作出y=sin x与y=的图象,如图.
由图可知,当x≥5π时,>1>sin x,所以此时两函数图象无交点;
当0
所以函数f(x)的零点个数为5+5+1=11.
4.D 函数f(x)在区间≤0,即(1-loga2)·(1-loga3)≤0,
则
解得2≤a≤3,
当a=3时,f(x)=(6x-1)2-log3(3x+2),
显然函数f(x)在区间上有两个零点,不符合
题意.
经检验,当a=2时,符合题意.
故实数a的取值范围为[2,3).故选D.
5.BD 由题知,f(x)在x∈(-∞,0]上单调递增,其值域为(-∞,1];
f(x)在(0,1]上单调递减,其值域为[0,+∞);
f(x)在(1,+∞)上单调递增,其值域为(0,+∞).
作出y=f(x)的图象,如图所示:
∵g(x)=f[2f(x)]+a有7个零点,即f[2f(x)]=-a有7个不同的解,
当-a<0时,有2f(x)<-1,即f(x)<-,此时g(x)有1个零点;
当-a=0时,有2f(x)=±1,即f(x)=±,
∴f(x)=-有3个解,
此时g(x)共有4个零点;
当0<-a≤lg 2时,有-1<2f(x)≤lg 2-1或≤2f(x)<1或1<2f(x)≤2,
∴-
∴
当-a>1时,有0<2f(x)<或2f(x)>10,
∴0
综上,要使g(x)有7个零点,则-lg 2≤a<0.
结合选项知,a的可能取值是-.
故选BD.
6.答案
解析 由题意得≤a≤,
作出函数y=f(x)与y=2-的图象,如图所示:
若f(x)=2-,故a∈.
7.解析 (1)根据题意画出函数f(x)的图象,如图所示:
由图象可知,当且仅当a=2或a=-2时,直线y=a与函数y=f(x)的图象有三个不同的交点,即函数g(x)恰有三个不同的零点,故a=2或a=-2.
(2)由(1)中f(x)的图象可知,当-1
当-1
故当-1
又f(x)=lg,
f(-x)=lg,
所以lg=0,
即lg=0,
所以=1,
所以(m+1)2=1,
又m<0,所以m=-2.
(2)由(1)可得f(x)=lg.
令-1+>0,得-1
函数g(x)=f(x)-lg(4x+a-4)有零点,即g(x)=0有实数根,
即lg与y=4x+a-4=4(x-1)+a的图象在(-1,1)上有交点.画出两个函数在(-1,1)上的大致图象,如图所示.
易知y=4(x-1)+a过定点(1,a),且斜率为4,所以由图可知a>0.
1
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
