苏教版(2019)高中数学必修一8.2.1 几个函数模型的比较同步练习(Word含答案)
文档属性
| 名称 | 苏教版(2019)高中数学必修一8.2.1 几个函数模型的比较同步练习(Word含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 123.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-06 15:59:46 | ||
图片预览

文档简介
8.2 函数与数学模型
8.2.1 几个函数模型的比较
基础过关练
题组 不同函数增长的差异
1.(2022江苏射阳中学月考)下面对函数f(x)=lox,g(x)=与h(x)=-在区间(0,+∞)上递减情况的说法中正确的是( )
A.f(x)递减速度越来越慢,g(x)递减速度越来越快,h(x)递减速度比较
平稳
f(x)递减速度越来越快,g(x)递减速度越来越慢,h(x)递减速度越来
越快
f(x)递减速度越来越慢,g(x)递减速度越来越慢,h(x)递减速度比较
平稳
f(x)递减速度越来越快,g(x)递减速度越来越快,h(x)递减速度越来
越快
2.(2020湖南醴陵一中期中)已知函数y1=2x,y2=x2,y3=log2x,在区间(0,+∞)上一定存在x0,当x>x0时( )
A.2x>x2>log2x B.x2>2x>log2x
C.log2x>2x>x2 D.log2x>x2>2x
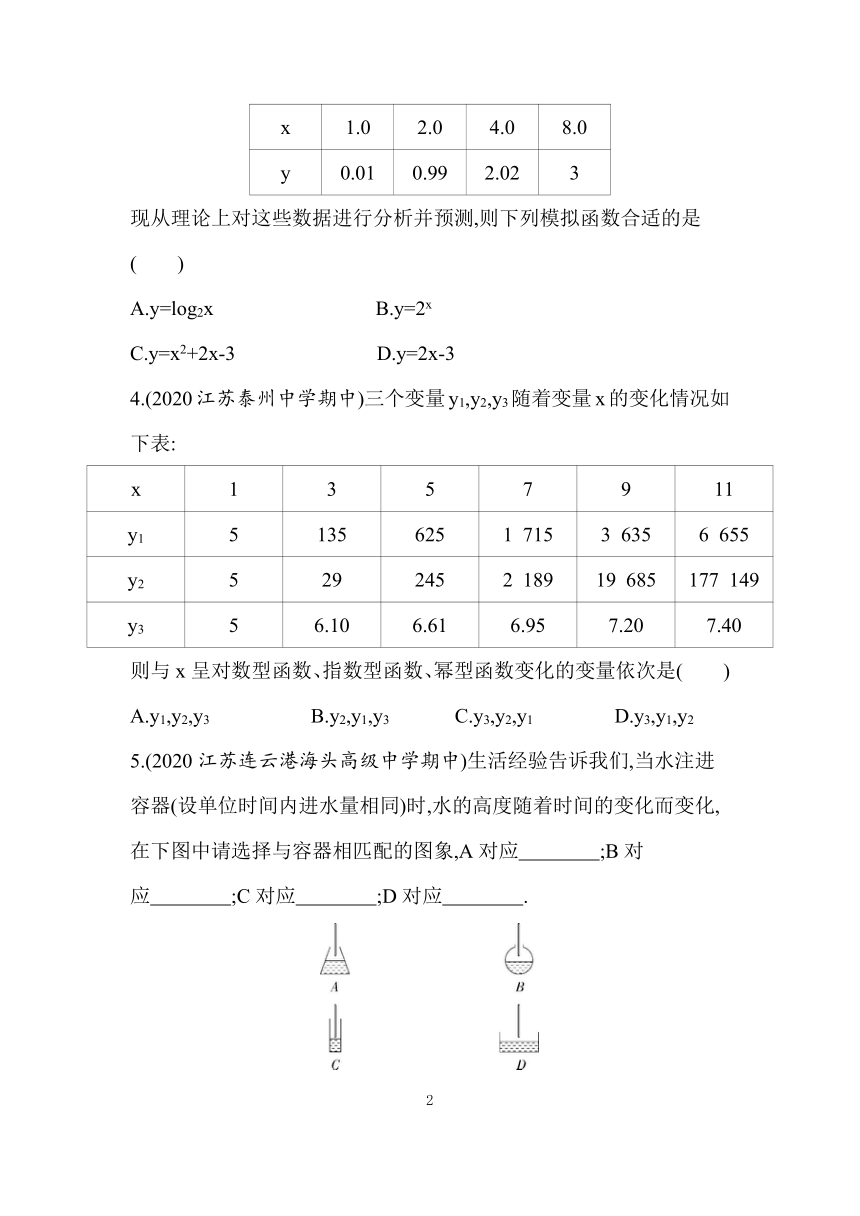
3.(2022江苏如东高级中学月考)某同学参加研究性学习活动,得到如下试验数据:
x 1.0 2.0 4.0 8.0
y 0.01 0.99 2.02 3
现从理论上对这些数据进行分析并预测,则下列模拟函数合适的是( )
A.y=log2x B.y=2x
C.y=x2+2x-3 D.y=2x-3
4.(2020江苏泰州中学期中)三个变量y1,y2,y3随着变量x的变化情况如下表:
x 1 3 5 7 9 11
y1 5 135 625 1 715 3 635 6 655
y2 5 29 245 2 189 19 685 177 149
y3 5 6.10 6.61 6.95 7.20 7.40
则与x呈对数型函数、指数型函数、幂型函数变化的变量依次是( )
A.y1,y2,y3 B.y2,y1,y3 C.y3,y2,y1 D.y3,y1,y2
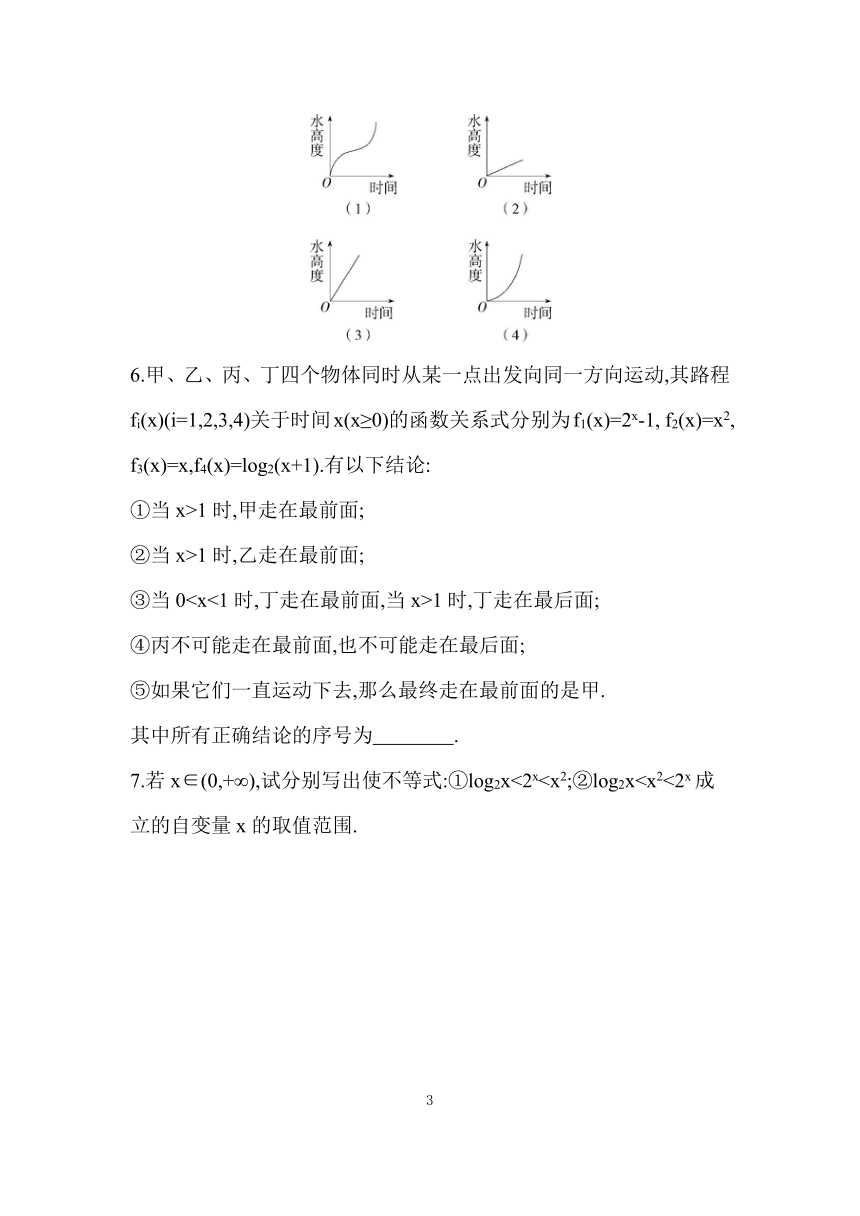
5.(2020江苏连云港海头高级中学期中)生活经验告诉我们,当水注进容器(设单位时间内进水量相同)时,水的高度随着时间的变化而变化,在下图中请选择与容器相匹配的图象,A对应 ;B对应 ;C对应 ;D对应 .
6.甲、乙、丙、丁四个物体同时从某一点出发向同一方向运动,其路程fi(x)(i=1,2,3,4)关于时间x(x≥0)的函数关系式分别为f1(x)=2x-1, f2(x)=x2, f3(x)=x,f4(x)=log2(x+1).有以下结论:
①当x>1时,甲走在最前面;
②当x>1时,乙走在最前面;
③当01时,丁走在最后面;
④丙不可能走在最前面,也不可能走在最后面;
⑤如果它们一直运动下去,那么最终走在最前面的是甲.
其中所有正确结论的序号为 .
7.若x∈(0,+∞),试分别写出使不等式:①log2x<2x8.函数f(x)=2x和g(x)=x3的大致图象如图所示.设两函数的图象交于点A(x1,y1),B(x2,y2),且x1(1)请指出图中曲线C1,C2分别对应的函数;
(2)结合函数图象,比较f(6),g(6),f(2 021),g(2 021)的大小.
答案全解全析
基础过关练
1.C 2.A 3.A 4.C
1.C 画出函数f(x)、g(x)、h(x)在区间(0,+∞)上的图象,如图所示:
函数f(x)的图象在区间(0,1)上递减较快,但递减速度逐渐变慢;在区间(1,+∞)上,递减较慢,且越来越慢;函数g(x)的图象在区间(0,+∞)上递减较慢,且递减速度越来越慢;函数h(x)的图象递减速度比较平稳.故选C.
2.A 由于指数函数增长最快,对数函数增长最慢,因此当x很大时,指数函数值最大,对数函数值最小,
即在区间(0,+∞)上一定存在x0,当x>x0时,2x>x2>log2x,故选A.
3.A 由题表可得y随x的增大而增大,且增大的幅度越来越小,而函数y=2x,y=x2+2x-3在(0,+∞)上的增大幅度越来越大,函数y=2x-3呈线性增大,只有函数y=log2x与已知数据的增大趋势接近.故选A.
4.C
5.答案 (4);(1);(3);(2)
解析 A容器下粗上细,水的高度的变化先慢后快,故与(4)对应;B容器为球形,水的高度的变化为快→慢→快,故与(1)对应;C,D容器都是柱形,水的高度的变化都是直线形,但C容器细,D容器粗,故C容器中水的高度的变化快,与(3)对应,D容器中水的高度的变化慢,与(2)对应.
6.答案 ③④⑤
解析 四个函数的大致图象如图所示,根据图象易知,③④⑤正确.
7.解析 在同一平面直角坐标系中作出函数y=2x,y=x2,y=log2x的图象,可得22=4,24=42=16,下面借助图象解决问题.
①∵log2x<2x∴自变量x的取值范围为(2,4).
②∵log2x4,
∴自变量x的取值范围为(0,2)∪(4,+∞).
8.解析 (1)曲线C1对应的函数为g(x)=x3,曲线C2对应的函数为f(x)=2x.
(2)∵f(1)=2>g(1)=1,f(2)=4g(10)=1 000,
∴1∴x1<6x2.
由题图可以看出,当x1f(x)当x>x2时,f(x)>g(x),
∴f(2 021)>g(2 021).
又g(2 021)>g(6),
∴f(2 021)>g(2 021)>g(6)>f(6).
1
8.2.1 几个函数模型的比较
基础过关练
题组 不同函数增长的差异
1.(2022江苏射阳中学月考)下面对函数f(x)=lox,g(x)=与h(x)=-在区间(0,+∞)上递减情况的说法中正确的是( )
A.f(x)递减速度越来越慢,g(x)递减速度越来越快,h(x)递减速度比较
平稳
f(x)递减速度越来越快,g(x)递减速度越来越慢,h(x)递减速度越来
越快
f(x)递减速度越来越慢,g(x)递减速度越来越慢,h(x)递减速度比较
平稳
f(x)递减速度越来越快,g(x)递减速度越来越快,h(x)递减速度越来
越快
2.(2020湖南醴陵一中期中)已知函数y1=2x,y2=x2,y3=log2x,在区间(0,+∞)上一定存在x0,当x>x0时( )
A.2x>x2>log2x B.x2>2x>log2x
C.log2x>2x>x2 D.log2x>x2>2x
3.(2022江苏如东高级中学月考)某同学参加研究性学习活动,得到如下试验数据:
x 1.0 2.0 4.0 8.0
y 0.01 0.99 2.02 3
现从理论上对这些数据进行分析并预测,则下列模拟函数合适的是( )
A.y=log2x B.y=2x
C.y=x2+2x-3 D.y=2x-3
4.(2020江苏泰州中学期中)三个变量y1,y2,y3随着变量x的变化情况如下表:
x 1 3 5 7 9 11
y1 5 135 625 1 715 3 635 6 655
y2 5 29 245 2 189 19 685 177 149
y3 5 6.10 6.61 6.95 7.20 7.40
则与x呈对数型函数、指数型函数、幂型函数变化的变量依次是( )
A.y1,y2,y3 B.y2,y1,y3 C.y3,y2,y1 D.y3,y1,y2
5.(2020江苏连云港海头高级中学期中)生活经验告诉我们,当水注进容器(设单位时间内进水量相同)时,水的高度随着时间的变化而变化,在下图中请选择与容器相匹配的图象,A对应 ;B对应 ;C对应 ;D对应 .
6.甲、乙、丙、丁四个物体同时从某一点出发向同一方向运动,其路程fi(x)(i=1,2,3,4)关于时间x(x≥0)的函数关系式分别为f1(x)=2x-1, f2(x)=x2, f3(x)=x,f4(x)=log2(x+1).有以下结论:
①当x>1时,甲走在最前面;
②当x>1时,乙走在最前面;
③当0
④丙不可能走在最前面,也不可能走在最后面;
⑤如果它们一直运动下去,那么最终走在最前面的是甲.
其中所有正确结论的序号为 .
7.若x∈(0,+∞),试分别写出使不等式:①log2x<2x
(2)结合函数图象,比较f(6),g(6),f(2 021),g(2 021)的大小.
答案全解全析
基础过关练
1.C 2.A 3.A 4.C
1.C 画出函数f(x)、g(x)、h(x)在区间(0,+∞)上的图象,如图所示:
函数f(x)的图象在区间(0,1)上递减较快,但递减速度逐渐变慢;在区间(1,+∞)上,递减较慢,且越来越慢;函数g(x)的图象在区间(0,+∞)上递减较慢,且递减速度越来越慢;函数h(x)的图象递减速度比较平稳.故选C.
2.A 由于指数函数增长最快,对数函数增长最慢,因此当x很大时,指数函数值最大,对数函数值最小,
即在区间(0,+∞)上一定存在x0,当x>x0时,2x>x2>log2x,故选A.
3.A 由题表可得y随x的增大而增大,且增大的幅度越来越小,而函数y=2x,y=x2+2x-3在(0,+∞)上的增大幅度越来越大,函数y=2x-3呈线性增大,只有函数y=log2x与已知数据的增大趋势接近.故选A.
4.C
5.答案 (4);(1);(3);(2)
解析 A容器下粗上细,水的高度的变化先慢后快,故与(4)对应;B容器为球形,水的高度的变化为快→慢→快,故与(1)对应;C,D容器都是柱形,水的高度的变化都是直线形,但C容器细,D容器粗,故C容器中水的高度的变化快,与(3)对应,D容器中水的高度的变化慢,与(2)对应.
6.答案 ③④⑤
解析 四个函数的大致图象如图所示,根据图象易知,③④⑤正确.
7.解析 在同一平面直角坐标系中作出函数y=2x,y=x2,y=log2x的图象,可得22=4,24=42=16,下面借助图象解决问题.
①∵log2x<2x
②∵log2x
∴自变量x的取值范围为(0,2)∪(4,+∞).
8.解析 (1)曲线C1对应的函数为g(x)=x3,曲线C2对应的函数为f(x)=2x.
(2)∵f(1)=2>g(1)=1,f(2)=4
∴1
由题图可以看出,当x1
∴f(2 021)>g(2 021).
又g(2 021)>g(6),
∴f(2 021)>g(2 021)>g(6)>f(6).
1
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
