2022-2023学年人教版八年级上册数学11.1.1三角形的边 课件(共27张PPT)
文档属性
| 名称 | 2022-2023学年人教版八年级上册数学11.1.1三角形的边 课件(共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 975.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-05 16:34:04 | ||
图片预览








文档简介
(共27张PPT)
第
11.1.1 三角形的边
LOGO
ADD YOUR SCHOOL NAME
十
一
章
11.1 与三角形有关的线段
01
PART ONE
学习目标
1. 认识三角形的边、内角、顶点,能用几何语言表示三角形;
3. 了解三角形分类的原则和结论.(重点)
2. 掌握三角形的三边关系定理,能利用定理及其推论进行简单的证明;(难点)
导入新课
Teacher says lesson
看一看
法国卢浮宫
导入新课
Teacher says lesson
埃及金字塔
新奥尔良三角大夏
导入新课
Teacher says lesson
钢架桥宫
水分子结构示意图
课程分析/
Teacher says lesson
(1)从古埃及的金字塔到现代的飞机,从宏伟的建筑
物到微小的分子结构,都有三角形的形象,为什么在工程 建筑、机械制造中经常采用三角形呢?
问题
讲授新课
Teacher says lesson
问题1:观察三角形的形成过程,说一说什么叫三角形
定义:
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
A
B
C
三角形的相关概念
讲授新课
Teacher says lesson
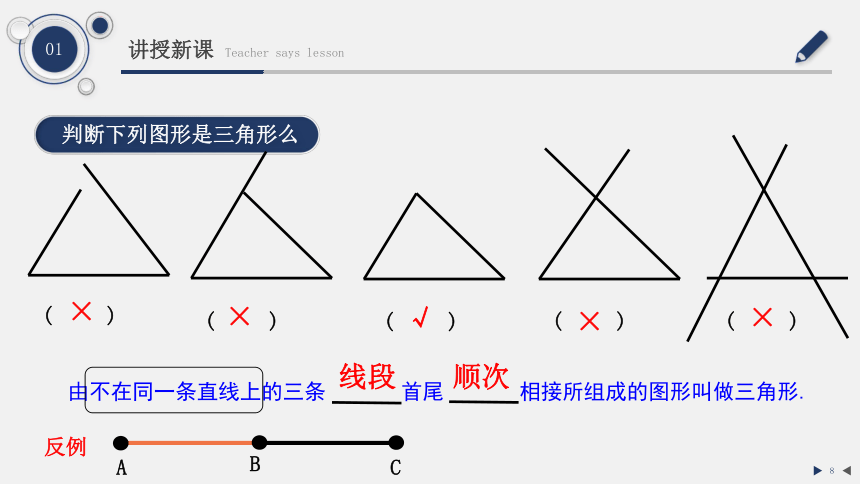
判断下列图形是三角形么
( )
( )
( )
( )
( )
×
×
×
×
√
由不在同一条直线上的三条 首尾 相接所组成的图形叫做三角形.
线段
顺次
A
B
C
反例
新授课
Teacher says lesson
边:线段 AB,BC,CA 是三角形的边.
顶点:点 A,B,C 是三角形的顶点.
角:∠A,∠B,∠C 叫做三角形的内角,简称三角形的角.
问题2:三角形中有几条线段 有几个角
A
B
C
边
边
边
顶点
顶点
顶点
角
三角形的相关概念
顶点是A、B、C的三角形,记作△ABC,读作:三角形ABC
答:有三条线段,三个角
新课讲授
Teacher says lesson
三角形的相关概念
如图,顶点A所对应的边BC用 a表示
AC
c
b
a
顶点 C
角
角
角
顶点 A
顶点 B
b
∠B所对的边 可以用 表示
AB所对的角是 ,AB可以用 表示
∠C
c
新课讲授
Teacher says lesson
三角形的相关概念
顶点
边
内角
点A 点B 点C
BC
AC
AB
c
b
a
∠A
∠B
∠C
c
b
a
C
A
B
课堂练习
Teacher says lesson
A
B
D
C
例:如图所示,共有 个三角形,用符号表示这些三角形为
△ABD的角有
以AC为边的三角形有
以D为顶点的三角形有
∠C是△ADC的 边的对角;
BD是△ABD中∠ 的对边。
新课讲授
Teacher says lesson
问题1:观察下列三角形,说一说,按照三角形内角的大小,三角形可以分为哪几类?
锐角三角形、 直角三角形、 钝角三角形.
三角形分类
新课讲授
Teacher says lesson
想一想,如何按照边的关系对三角形进行分类呢?
三边都不相等的三角形
三角形分类
等腰三角形
腰
腰
底边
顶角
低角
低角
等边三角形
新课讲授
Teacher says lesson
三角形分类
按是否有相等边分类
三角形
三边都不相等的三角形
等腰
三角形
底边和腰不相等的等腰三角形
等边三角形
按最大内角分类
三角形
锐角三角形
直角三角形
钝角三角形
课堂练习/
Teacher says lesson
判断:
(2)等边三角形是特殊的等腰三角形.( )
(1)一个钝角三角形一定不是等腰三角形.( )
√
×
(3)等腰三角形的腰和底一定不相等.( )
×
(4)等边三角形是锐角三角形.( )
(5)直角三角形一定不是等腰三角形.( )
×
√
新课讲授
Teacher says lesson
做一做 如图,在 B 点的小明,为了尽快到 C 点的学校,它选择了 B C 的路线,而不选择 B A C的路线,如果你是小明你会选择哪条路?
C
A
B
AB + AC > BC
三角形的三边关系
同理:
AC + BC> AB
AB + BC > AC
三角形两边的和大于第三边.
(两点之间线段最短)
新课讲授
Teacher says lesson
C
A
B
AB + AC > BC
三角形的三边关系
同理:
AC + BC> AB
AB + BC > AC
三角形两边的和大于第三边.
BC> AB-AC
BC > AC-AB
三角形两边的差小于第三边
新课讲授
Teacher says lesson
三角形的三边关系
三角形两边的和大于 ;
(可用来判断三条线段能否组成三角形)
三角形两边的差小于 ;
进而得到,三角形第三边的取值范围
两边的差<第三边<两边的和
课堂练习
Teacher says lesson
例1 下列长度的三条线段能否拼成三角形?为什么?
(1)3 cm、8 cm、4 cm;(2)5 cm、6 cm、11 cm;
(3)5 cm、6 cm、10 cm.
解:(1)不能,∵ 3 cm + 4 cm < 8 cm.
(2)不能,∵ 5 cm + 6 cm = 11 cm.
(3)能,∵ 5 cm + 6 cm > 10 cm.
判断三条线段是否可以组成三角形,只需判断两条较短线段长之和是否大于第三条线段长即可.
归纳
课堂练习
Teacher says lesson
一根木棒长为 7,另一根木棒长为 2,那么用长度为 4 的木棒能和它们首尾相连拼成三角形吗?长度为 11 的木棒呢?若不能拼成,则第三根木棒长应在什么范围?
三角形的第三边长 x 满足两边之差<x<两边之和.
设第三根木棒长为 x,则应有
7 - 2 < x < 7 + 2,
即 5 < x < 9.
答:用长度为 4 或 11 的木棒都不能和它们拼成三角形. 第三根木棒长的范围为 5 < x < 9.
归纳
解:7,、2、4不能拼成三角形,∵2+4<7 ;7、2、11不能拼成三角 形,∵7+2<11
课堂练习
Teacher says lesson
例2 用一条长为 18 cm 的细绳围成一个等腰三角形.
(1) 如果腰长是底边长的 2 倍,那么各边的长是多少?
(2) 能围成有一边的长是 4 cm 的等腰三角形吗?为什么?
解:(1) 设底边长为 x cm,则腰长为 2x cm,
∴ x + 2x + 2x = 18,解得 x = 3.6.
∴ 三边长分别为 3.6 cm、7.2 cm、7.2 cm.
(2) ∵ 长为 4 cm 的边可能是腰,也可能是底边,
∴ 需要分情况讨论:
① 若底边长为 4 cm,设腰长为 x cm,则有
4 + 2x = 18,解得 x = 7.
例题讲解
Teacher says lesson
例2 用一条长为 18 cm 的细绳围成一个等腰三角形.
(1) 如果腰长是底边长的 2 倍,那么各边的长是多少?
(2) 能围成有一边的长是 4 cm 的等腰三角形吗?为什么?
②若腰长为 4 cm,设底边长为 x cm,则有 2×4 + x = 18,解得 x = 10.
∵ 4 + 4<10,不符合三角形三边关系,
∴ 该情况不存在.
综上可知,可以围成底边长是 4 cm,腰长是 7 cm 的等腰三角形.
等腰三角形与三角形的三边关系结合时,若腰和底不明确,需要分类讨论,再检验是否符合三边关系.
归纳
课堂练习
Teacher says lesson
1. 图中的锐角三角形有 ( )
A. 3 个 B. 4 个 C. 5 个 D. 6 个
A
2. 用木棒钉成一个三角架,两根小棒长分别是
7 cm 和 10 cm,第三根小棒长可取 ( )
A. 2 cm B. 3 cm C. 11 cm D. 20 cm
C
课堂练习
Teacher says lesson
3. 如图,在△ACE 中,∠CAE 的对边是 .
A
B
F
E
D
C
CE
课堂小结
三角形
定义及其基本要素
顶点、角、边
分类
按边分类
按角分类
不重不漏
三边关系
原理
两点之间,线段最短
应用
内容
两边之和大于第三边
两边之差小于第三边
a-bb,x 为第三边)
THANKS
第
11.1.1 三角形的边
LOGO
ADD YOUR SCHOOL NAME
十
一
章
11.1 与三角形有关的线段
01
PART ONE
学习目标
1. 认识三角形的边、内角、顶点,能用几何语言表示三角形;
3. 了解三角形分类的原则和结论.(重点)
2. 掌握三角形的三边关系定理,能利用定理及其推论进行简单的证明;(难点)
导入新课
Teacher says lesson
看一看
法国卢浮宫
导入新课
Teacher says lesson
埃及金字塔
新奥尔良三角大夏
导入新课
Teacher says lesson
钢架桥宫
水分子结构示意图
课程分析/
Teacher says lesson
(1)从古埃及的金字塔到现代的飞机,从宏伟的建筑
物到微小的分子结构,都有三角形的形象,为什么在工程 建筑、机械制造中经常采用三角形呢?
问题
讲授新课
Teacher says lesson
问题1:观察三角形的形成过程,说一说什么叫三角形
定义:
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
A
B
C
三角形的相关概念
讲授新课
Teacher says lesson
判断下列图形是三角形么
( )
( )
( )
( )
( )
×
×
×
×
√
由不在同一条直线上的三条 首尾 相接所组成的图形叫做三角形.
线段
顺次
A
B
C
反例
新授课
Teacher says lesson
边:线段 AB,BC,CA 是三角形的边.
顶点:点 A,B,C 是三角形的顶点.
角:∠A,∠B,∠C 叫做三角形的内角,简称三角形的角.
问题2:三角形中有几条线段 有几个角
A
B
C
边
边
边
顶点
顶点
顶点
角
三角形的相关概念
顶点是A、B、C的三角形,记作△ABC,读作:三角形ABC
答:有三条线段,三个角
新课讲授
Teacher says lesson
三角形的相关概念
如图,顶点A所对应的边BC用 a表示
AC
c
b
a
顶点 C
角
角
角
顶点 A
顶点 B
b
∠B所对的边 可以用 表示
AB所对的角是 ,AB可以用 表示
∠C
c
新课讲授
Teacher says lesson
三角形的相关概念
顶点
边
内角
点A 点B 点C
BC
AC
AB
c
b
a
∠A
∠B
∠C
c
b
a
C
A
B
课堂练习
Teacher says lesson
A
B
D
C
例:如图所示,共有 个三角形,用符号表示这些三角形为
△ABD的角有
以AC为边的三角形有
以D为顶点的三角形有
∠C是△ADC的 边的对角;
BD是△ABD中∠ 的对边。
新课讲授
Teacher says lesson
问题1:观察下列三角形,说一说,按照三角形内角的大小,三角形可以分为哪几类?
锐角三角形、 直角三角形、 钝角三角形.
三角形分类
新课讲授
Teacher says lesson
想一想,如何按照边的关系对三角形进行分类呢?
三边都不相等的三角形
三角形分类
等腰三角形
腰
腰
底边
顶角
低角
低角
等边三角形
新课讲授
Teacher says lesson
三角形分类
按是否有相等边分类
三角形
三边都不相等的三角形
等腰
三角形
底边和腰不相等的等腰三角形
等边三角形
按最大内角分类
三角形
锐角三角形
直角三角形
钝角三角形
课堂练习/
Teacher says lesson
判断:
(2)等边三角形是特殊的等腰三角形.( )
(1)一个钝角三角形一定不是等腰三角形.( )
√
×
(3)等腰三角形的腰和底一定不相等.( )
×
(4)等边三角形是锐角三角形.( )
(5)直角三角形一定不是等腰三角形.( )
×
√
新课讲授
Teacher says lesson
做一做 如图,在 B 点的小明,为了尽快到 C 点的学校,它选择了 B C 的路线,而不选择 B A C的路线,如果你是小明你会选择哪条路?
C
A
B
AB + AC > BC
三角形的三边关系
同理:
AC + BC> AB
AB + BC > AC
三角形两边的和大于第三边.
(两点之间线段最短)
新课讲授
Teacher says lesson
C
A
B
AB + AC > BC
三角形的三边关系
同理:
AC + BC> AB
AB + BC > AC
三角形两边的和大于第三边.
BC> AB-AC
BC > AC-AB
三角形两边的差小于第三边
新课讲授
Teacher says lesson
三角形的三边关系
三角形两边的和大于 ;
(可用来判断三条线段能否组成三角形)
三角形两边的差小于 ;
进而得到,三角形第三边的取值范围
两边的差<第三边<两边的和
课堂练习
Teacher says lesson
例1 下列长度的三条线段能否拼成三角形?为什么?
(1)3 cm、8 cm、4 cm;(2)5 cm、6 cm、11 cm;
(3)5 cm、6 cm、10 cm.
解:(1)不能,∵ 3 cm + 4 cm < 8 cm.
(2)不能,∵ 5 cm + 6 cm = 11 cm.
(3)能,∵ 5 cm + 6 cm > 10 cm.
判断三条线段是否可以组成三角形,只需判断两条较短线段长之和是否大于第三条线段长即可.
归纳
课堂练习
Teacher says lesson
一根木棒长为 7,另一根木棒长为 2,那么用长度为 4 的木棒能和它们首尾相连拼成三角形吗?长度为 11 的木棒呢?若不能拼成,则第三根木棒长应在什么范围?
三角形的第三边长 x 满足两边之差<x<两边之和.
设第三根木棒长为 x,则应有
7 - 2 < x < 7 + 2,
即 5 < x < 9.
答:用长度为 4 或 11 的木棒都不能和它们拼成三角形. 第三根木棒长的范围为 5 < x < 9.
归纳
解:7,、2、4不能拼成三角形,∵2+4<7 ;7、2、11不能拼成三角 形,∵7+2<11
课堂练习
Teacher says lesson
例2 用一条长为 18 cm 的细绳围成一个等腰三角形.
(1) 如果腰长是底边长的 2 倍,那么各边的长是多少?
(2) 能围成有一边的长是 4 cm 的等腰三角形吗?为什么?
解:(1) 设底边长为 x cm,则腰长为 2x cm,
∴ x + 2x + 2x = 18,解得 x = 3.6.
∴ 三边长分别为 3.6 cm、7.2 cm、7.2 cm.
(2) ∵ 长为 4 cm 的边可能是腰,也可能是底边,
∴ 需要分情况讨论:
① 若底边长为 4 cm,设腰长为 x cm,则有
4 + 2x = 18,解得 x = 7.
例题讲解
Teacher says lesson
例2 用一条长为 18 cm 的细绳围成一个等腰三角形.
(1) 如果腰长是底边长的 2 倍,那么各边的长是多少?
(2) 能围成有一边的长是 4 cm 的等腰三角形吗?为什么?
②若腰长为 4 cm,设底边长为 x cm,则有 2×4 + x = 18,解得 x = 10.
∵ 4 + 4<10,不符合三角形三边关系,
∴ 该情况不存在.
综上可知,可以围成底边长是 4 cm,腰长是 7 cm 的等腰三角形.
等腰三角形与三角形的三边关系结合时,若腰和底不明确,需要分类讨论,再检验是否符合三边关系.
归纳
课堂练习
Teacher says lesson
1. 图中的锐角三角形有 ( )
A. 3 个 B. 4 个 C. 5 个 D. 6 个
A
2. 用木棒钉成一个三角架,两根小棒长分别是
7 cm 和 10 cm,第三根小棒长可取 ( )
A. 2 cm B. 3 cm C. 11 cm D. 20 cm
C
课堂练习
Teacher says lesson
3. 如图,在△ACE 中,∠CAE 的对边是 .
A
B
F
E
D
C
CE
课堂小结
三角形
定义及其基本要素
顶点、角、边
分类
按边分类
按角分类
不重不漏
三边关系
原理
两点之间,线段最短
应用
内容
两边之和大于第三边
两边之差小于第三边
a-b
THANKS
