2022-2023学年人教版八年级数学上册13.3.1等腰三角形 课件(共16张PPT)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册13.3.1等腰三角形 课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-05 16:59:43 | ||
图片预览


文档简介
(共16张PPT)
13.3.1 等腰三角形
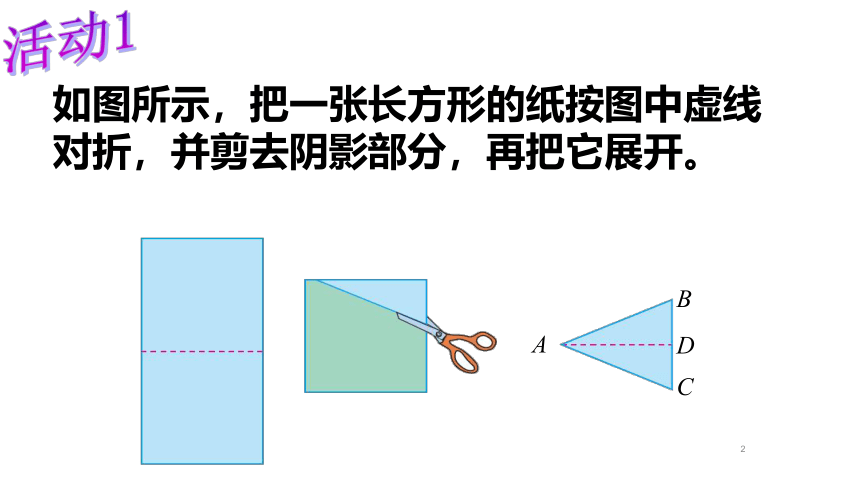
如图所示,把一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它展开。ABCD活动1有两条边相等的三角形叫做
等腰三角形。
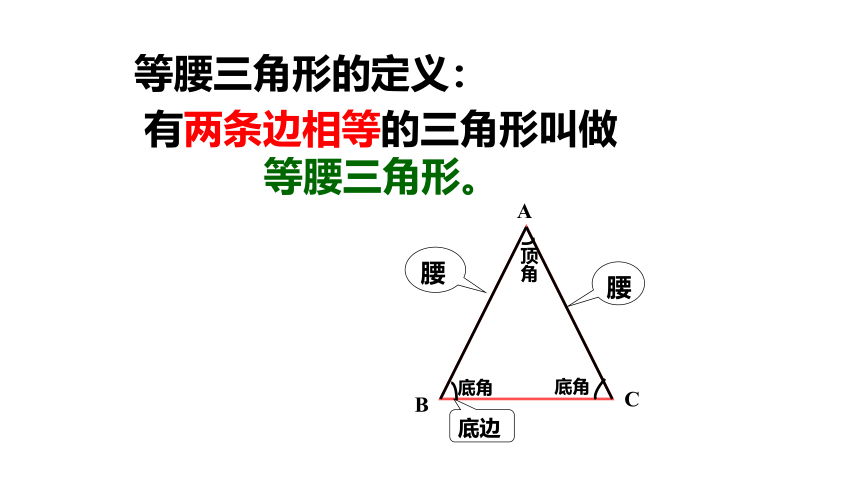
等腰三角形的定义:
A
C
B
腰
腰
底边
底角
底角
顶角
A
B
C
D
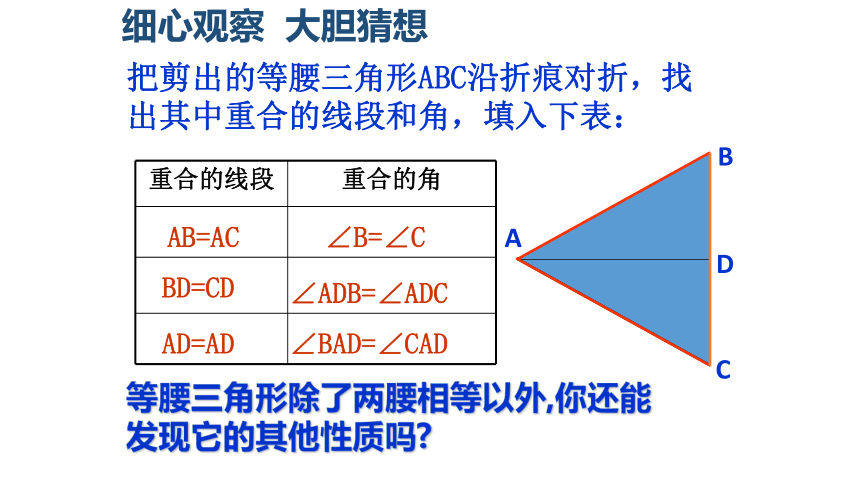
把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角,填入下表:
重合的线段 重合的角
等腰三角形除了两腰相等以外,你还能发现它的其他性质吗
AB=AC
BD=CD
AD=AD
∠B=∠C
∠ADB=∠ADC
∠BAD=∠CAD
细心观察 大胆猜想
A
B
C
D
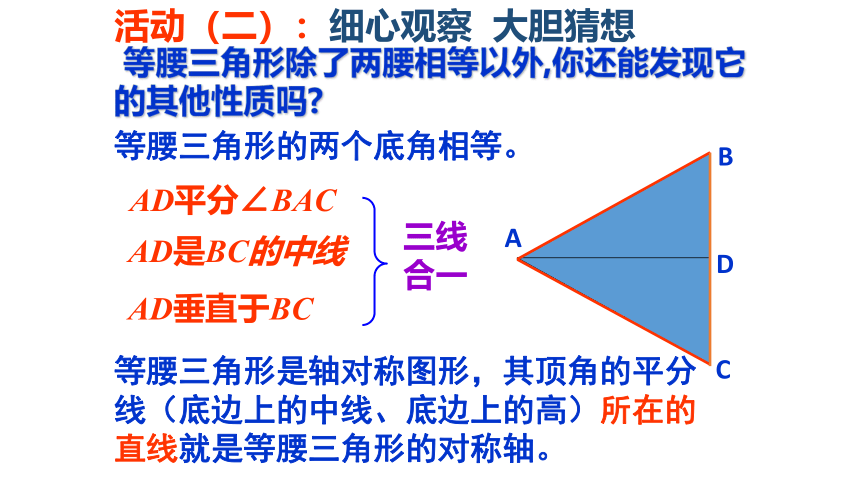
等腰三角形的两个底角相等。
等腰三角形是轴对称图形,其顶角的平分线(底边上的中线、底边上的高)所在的直线就是等腰三角形的对称轴。
等腰三角形除了两腰相等以外,你还能发现它的其他性质吗
AD平分∠BAC
AD是BC的中线
AD垂直于BC
三线合一
活动(二):细心观察 大胆猜想
猜想1:等腰三角形的两底角相等。
(简写成“等边对等角”)
猜想2:等腰三角形的顶角平分线,底边的中线和底边的高互相重合。
(简写成“三线合一”)
活动2
观察猜想
已知:△ABC中,AB=AC
求证:∠B=∠C
A
B
C
D
等腰三角形的两个底角相等
验证猜想1
活动3
已知: 在△ABC中,AB=AC.
求证: ∠B= ∠C.
A
B
C
D
证明:
过点A作顶角的角平分线AD,
则∠BAD=∠CAD.
AB=AC
∠BAD=∠CAD
AD=AD
∴ △BAD ≌ △CAD (SAS).
∴ ∠B= ∠C (全等三角形对应角相等).
方法一:作顶角的角平分线
在△BAD和△CAD中
证明
已知: 在△ABC中,AB=AC.
求证: ∠B= ∠C.
A
B
C
D
证明:
过点A作底边的中线AD,
则BD=CD.
AB=AC
BD=CD
AD=AD
∴ △BAD≌ △CAD (SSS).
∴ ∠B= ∠C (全等三角形对应角相等).
在△BAD和△CAD中
方法二:作底边上的中线
证明
证明:
过点A作底边高线AD.
则 ∠ADB=∠ADC =90
AB=AC ( 已知 ),
AD=AD (公共边) ,
∴ Rt △BAD ≌ Rt △CAD (HL).
∴ ∠ B= ∠C (全等三角形对应角相等).
已知: △ ABC中,AB=AC.
求证: ∠B= ∠C.
在Rt△BAD和△RtCAD中,
方法三:作底边的高线
A
B
C
D
证明
性质1:等腰三角形的两个底角相等
(简写成“等边对等角”).
A
B
C
符号语言:
∵ AB=AC
∴ ∠B=∠C (等边对等角)
(简写成等腰三角形三线合一)
性质2:等腰三角形的顶角平分线与底边上的中线,底边上的高互相重合.
底边上的高,
AD垂直于BC
底边上的中线
AD平分∠BAC
AD是BC的中线
顶角平分线
∠BAD= ∠ CAD
∠ADB= ∠ ADC=900
BD=CD
A
B
D
C
一般三角形是否具备三线合一的性质呢?
“三线合一”是等腰三角形所特有的性质。
1. 根据等腰三角形性质2填空,
在△ABC中, AB=AC,
小试牛刀
(1) ∵AD⊥BC,
∴∠_____ = ∠_____,____= ____.
(2) ∵AD是中线,∴____⊥____ ,∠_____ =∠_____.
(3) ∵AD是角平分线,∴____ ⊥____ ,_____ =_____.
A
B
C
D
BAD
CAD
CAD
BD
CD
AD
BC
BD
BAD
BC
AD
CD
知一线得二线
“三线合一”可以帮助我们解决线段的垂直、
线段的相等以及角的相等问题。
2、等腰三角形一个底角为70°, 它的顶角为______.
3、等腰三角形一个角为70°,它的另外两个角为_____________________.
4、等腰三角形一个角为110°,它的另外两个角为___________.
① 顶角度数+2×底角度数=180°
② 0°<顶角度数<180°
③ 0°<底角度数<90°
结论: 在等腰三角形中,
40 °
35 °,35 °
70°,40° 或 55°,55°
课堂小结
今天这节课你有收获吗 ?
2 等腰三角形的两条重要性质。
(1)等边对等角。
(2)三线合一。
1 等腰三角形的定义。
13.3.1 等腰三角形
如图所示,把一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它展开。ABCD活动1有两条边相等的三角形叫做
等腰三角形。
等腰三角形的定义:
A
C
B
腰
腰
底边
底角
底角
顶角
A
B
C
D
把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角,填入下表:
重合的线段 重合的角
等腰三角形除了两腰相等以外,你还能发现它的其他性质吗
AB=AC
BD=CD
AD=AD
∠B=∠C
∠ADB=∠ADC
∠BAD=∠CAD
细心观察 大胆猜想
A
B
C
D
等腰三角形的两个底角相等。
等腰三角形是轴对称图形,其顶角的平分线(底边上的中线、底边上的高)所在的直线就是等腰三角形的对称轴。
等腰三角形除了两腰相等以外,你还能发现它的其他性质吗
AD平分∠BAC
AD是BC的中线
AD垂直于BC
三线合一
活动(二):细心观察 大胆猜想
猜想1:等腰三角形的两底角相等。
(简写成“等边对等角”)
猜想2:等腰三角形的顶角平分线,底边的中线和底边的高互相重合。
(简写成“三线合一”)
活动2
观察猜想
已知:△ABC中,AB=AC
求证:∠B=∠C
A
B
C
D
等腰三角形的两个底角相等
验证猜想1
活动3
已知: 在△ABC中,AB=AC.
求证: ∠B= ∠C.
A
B
C
D
证明:
过点A作顶角的角平分线AD,
则∠BAD=∠CAD.
AB=AC
∠BAD=∠CAD
AD=AD
∴ △BAD ≌ △CAD (SAS).
∴ ∠B= ∠C (全等三角形对应角相等).
方法一:作顶角的角平分线
在△BAD和△CAD中
证明
已知: 在△ABC中,AB=AC.
求证: ∠B= ∠C.
A
B
C
D
证明:
过点A作底边的中线AD,
则BD=CD.
AB=AC
BD=CD
AD=AD
∴ △BAD≌ △CAD (SSS).
∴ ∠B= ∠C (全等三角形对应角相等).
在△BAD和△CAD中
方法二:作底边上的中线
证明
证明:
过点A作底边高线AD.
则 ∠ADB=∠ADC =90
AB=AC ( 已知 ),
AD=AD (公共边) ,
∴ Rt △BAD ≌ Rt △CAD (HL).
∴ ∠ B= ∠C (全等三角形对应角相等).
已知: △ ABC中,AB=AC.
求证: ∠B= ∠C.
在Rt△BAD和△RtCAD中,
方法三:作底边的高线
A
B
C
D
证明
性质1:等腰三角形的两个底角相等
(简写成“等边对等角”).
A
B
C
符号语言:
∵ AB=AC
∴ ∠B=∠C (等边对等角)
(简写成等腰三角形三线合一)
性质2:等腰三角形的顶角平分线与底边上的中线,底边上的高互相重合.
底边上的高,
AD垂直于BC
底边上的中线
AD平分∠BAC
AD是BC的中线
顶角平分线
∠BAD= ∠ CAD
∠ADB= ∠ ADC=900
BD=CD
A
B
D
C
一般三角形是否具备三线合一的性质呢?
“三线合一”是等腰三角形所特有的性质。
1. 根据等腰三角形性质2填空,
在△ABC中, AB=AC,
小试牛刀
(1) ∵AD⊥BC,
∴∠_____ = ∠_____,____= ____.
(2) ∵AD是中线,∴____⊥____ ,∠_____ =∠_____.
(3) ∵AD是角平分线,∴____ ⊥____ ,_____ =_____.
A
B
C
D
BAD
CAD
CAD
BD
CD
AD
BC
BD
BAD
BC
AD
CD
知一线得二线
“三线合一”可以帮助我们解决线段的垂直、
线段的相等以及角的相等问题。
2、等腰三角形一个底角为70°, 它的顶角为______.
3、等腰三角形一个角为70°,它的另外两个角为_____________________.
4、等腰三角形一个角为110°,它的另外两个角为___________.
① 顶角度数+2×底角度数=180°
② 0°<顶角度数<180°
③ 0°<底角度数<90°
结论: 在等腰三角形中,
40 °
35 °,35 °
70°,40° 或 55°,55°
课堂小结
今天这节课你有收获吗 ?
2 等腰三角形的两条重要性质。
(1)等边对等角。
(2)三线合一。
1 等腰三角形的定义。
