第十三章轴对称导学案(2013年秋新人教版八年级上)
文档属性
| 名称 | 第十三章轴对称导学案(2013年秋新人教版八年级上) |  | |
| 格式 | zip | ||
| 文件大小 | 871.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-04 15:19:24 | ||
图片预览




文档简介
轴对称
13.1.1 轴对称
学习目标
1、初步认识轴对称图形;判掌握关于某条直线成轴对称的两个图形的对应线段相等、对应角相等;
2、断一个图形是否是轴对称图形;理解轴对称图形和两个图形成轴对称这两个概念的区别与联系。
3、能够判别两个图形是否成轴对称。通过试验,归纳出轴对称图形概念,能用概念;培养良好的动手试验能力、归纳能力和语言表述能力。
重点:理解轴对称图形的概念;轴对称图形的对应线段相等、对应角相等
难点:判断图形是否是轴对称图形;两个图形成轴对称与轴对称图形两个概念的区别与联系。
一、预习新知P58
1、观察课本中的7副图片,你能找出它们的共同特征吗?
2、你能列举出一些现实生活中具有这种特征的物体和建筑物吗?
3、动手做一做:把一张纸对折,然后从折叠处剪出一个图形,展开后会是一个什么样的图形?它有什么特征?
4、如果一个图形沿一条__________折叠,________两旁的部分能够完全________.这个图形就叫做轴对称图形,这条________就是它的对称轴,这时,我们也说这个图形关于这条_________(成轴) 对称.
5、观察课本P59图13.1-3中的三幅图形,并试着沿虚线折叠,每对图形有什么共同特征?
6、一个图形沿着某条直线折叠,如果他能够与________重合,那么就说_______关于这条直线对称,这条直线叫做__________,折叠后________叫做对称点.
7、在课本中的图13.1-3的第三个图中,
(1)标出A、B、C的对称点,∠A、∠B、∠C的对应角,
(2)连接AA′,BB′,CC′,你发现这三条线段有什么关系?你找到规律了吗?
8、成轴对称的两个图形全等吗?为什么?
9、全等的两个图形成轴对称吗?试举例说明。(可以画图说明)
10、课本P60练习题
做下面的题,检验你预习的结果
1、轴对称图形的对称轴是一条___________
A直线 B射线 C线段
右面的图形是轴对称图形吗?如果是,指出对称轴。
二、课堂展示
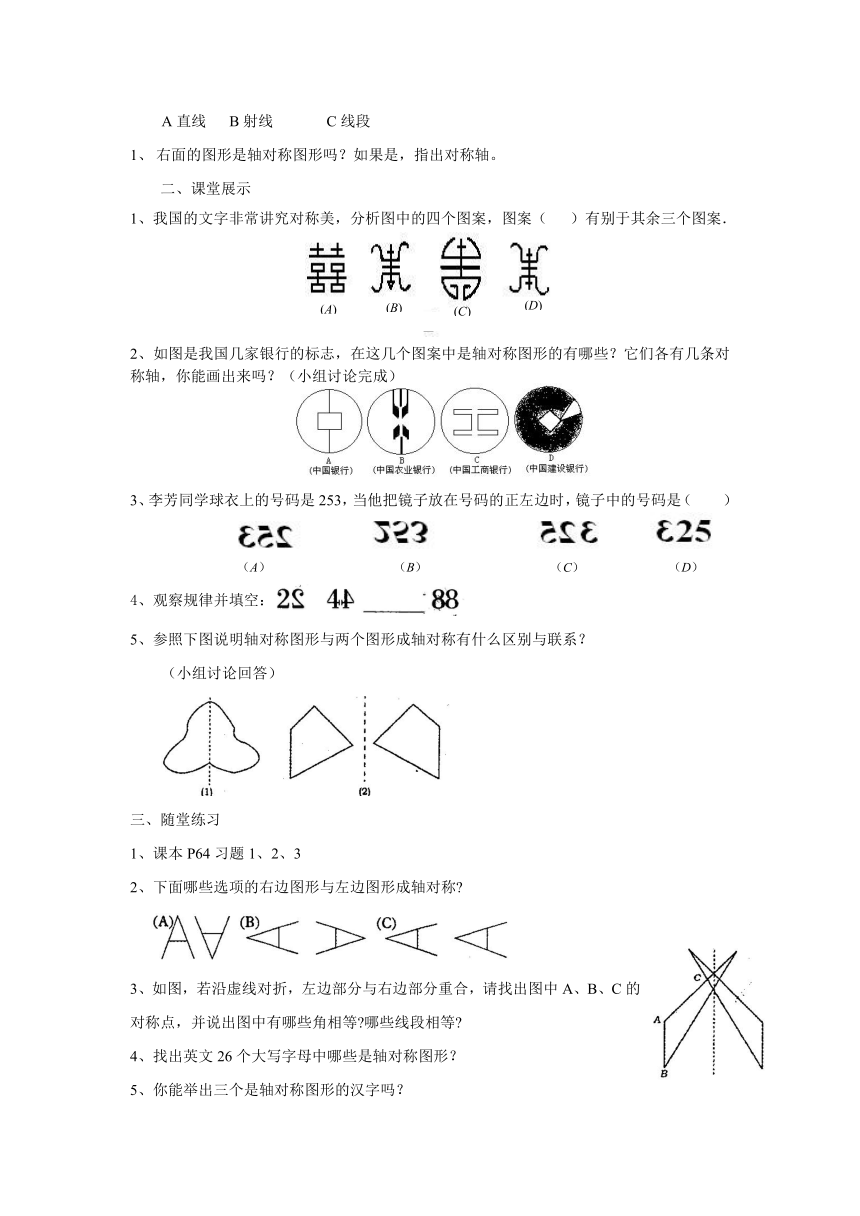
1、我国的文字非常讲究对称美,分析图中的四个图案,图案( )有别于其余三个图案.
2、如图是我国几家银行的标志,在这几个图案中是轴对称图形的有哪些?它们各有几条对称轴,你能画出来吗?(小组讨论完成)
3、李芳同学球衣上的号码是253,当他把镜子放在号码的正左边时,镜子中的号码是( )
4、观察规律并填空:
5、参照下图说明轴对称图形与两个图形成轴对称有什么区别与联系?
(小组讨论回答)
三、随堂练习
1、课本P64习题1、2、3
2、下面哪些选项的右边图形与左边图形成轴对称?
3、如图,若沿虚线对折,左边部分与右边部分重合,请找出图中A、B、C的对称点,并说出图中有哪些角相等?哪些线段相等?
4、找出英文26个大写字母中哪些是轴对称图形?
5、你能举出三个是轴对称图形的汉字吗?
6、你能运用学过的知识把下面这个数学中不可能的式子变为可能吗?
7、如图,四边形ABCD与四边形EFGH关于MN对称。
(1)A、B、C、D的对称点分别是 ,线段AC、AB的对应线段分别是 ,CD= , ∠CBA= ,∠ADC= .
(2)AE与BF平行吗?为什么?
(3)AE与BF平行,能说明轴对称图形对称点的连线一定互相平行吗?
(4)延长线段BC、FG,交于点P,延长线段AB、EF,交于点Q,,你有什么发现吗?
13.1.2线段的垂直平分线1
学习目标:
通过动手试验掌握线段的垂直平分线的定义
理解线段垂直平分线与对称轴的关系
掌握线段垂直平分线的性质
重点:线段垂直平分线上的点到线段两端的距离相等。
难点:运用线段垂直平分线性质解决问题。
教学过程
一、预习新知P61
1、线段是轴对称图形吗?通过折叠的方法作出线段AB的对称轴l,交AB与O
1)点A的对称点是_______
2)量出AO与BO的长度,它们有什么关系?
3)AB与直线l在位置上有什么关系?
2、经过线段________并且______于这条线段的________,叫做这条线段的垂直平分线.
3、观察课本P59思考中的图,线段AA′,BB′,CC′与直线MN的关系是________
由上可得:对称轴与对应点所连线段的垂直平分线有什么关系?
已知直线l垂直平分线段AB,交AB与O.点C是l上任意一点,连接AC,BC.
量出AC,BC的长度,它们有什么关系?
另在l上任找一点D,量出AD,DB的长度,它们有什么关系?
由1),2),你得到什么猜想?
4)用我们以前学过的只是证明你的猜想。
6、线段垂直平分线上的点与这条线段两个端点的__________。
7、.课本P62练习题1.
二、课堂展示
例1、已知互不平行的两条线段AB, A′B′关于直线l对称,AB, A′B′所在的直线交于点P,判断下列正误。
1)AB=A′B′( ) 2)点P在直线l上( )
3)若A, A′是对称点,则l垂直平分线段A A′( )
4)若B, B′是对称点,则PB=P B′( )
例2.如右图所示,△ABC中,BC=10,边BC的垂直平分线分别交AB、BC于点E、D,BE=6,求△BCE的周长。
三、随堂练习
1.如右图所示,直线MN和DE分别是线段 AB、BC的垂直平分线,它们交于P点,请问PA和 PC相等吗?为什么?
2、如图,△ABC中,AB=AC=18cm,BC= 10cm,AB的垂直平分线ED交AC于D点,求:△BCD的周长。
13.1.2 线段的垂直平分线2
学习目标:
进一步理解线段垂直平分线的性质,并能灵活运用。
掌握线段垂直平分线的判定
运用线段垂直平分线的判定解决问题
重点:探索并理解线段垂直平分线的判定
难点:运用线段垂直平分线的判定解决问题
一、预习新知P61
1、用一根木棒和一根弹性均匀的橡皮筋,做一个简易的弓,箭通过木棒中央的孔射出去。
(1) (2)
1)如图(1)要使CO垂直于AB,需要添加什么条件?为什么?
那么点C在_____________上。
2)如图(2),拉动C,到达D的位置,若AD=DB,那么点D在__________上。
3)由1),2),你得到什么猜想?
4)用学过的知识证明你的猜想。
2、与一条线段两个端点距离________的点,在这条线段的______________上。
3、课本P62练习题2
二、课堂展示
例、如图所示,已知Rt△ABC中,∠C=90°,沿过B点的一条直线BE折叠这个三角形,使C点落在AB边上的点D.要使点D恰为AB的中点,问还要添加什么条件?根据你添加的条件,你能证明出D为AB的中点吗?
三、随堂练习
1、如图:已知直线l和l异侧的两点A、B,在直线l上求作一点P,使PA=PB.
2、 如图:已知,OD=OC,ED=EC,那么直线OE是线段
CD的______________,你能写出证明过程吗/
3、已知:E是∠AOB的平分线上一点,EC⊥OA ,ED⊥OB ,垂足分别为C、D.
求证:(1)∠ECD=∠EDC ;(2)OE是CD的垂直平分线.
轴对称
学习目标:
掌握用“连结对称点的线段被对称轴垂直平分”
熟练画出轴对称图形的对称轴。
3、培养良好的动手实践能力。
重点:验证一个图形是不是轴对称图形
难点:画轴对称图形的对称轴。
一、预习新知P62—P63
1、如图:不通过折叠的方法,你能验证出这两个四边形是否关于直线MN对称吗?
2、设A、B两点关于直线MN对称,则______垂直平分________.
3、轴对称图形的对称轴与对应点所连线段的垂直平分线有什么关系?
4、作轴对称图形的对称轴就是做作出一对对应点所连线段_____________
5、只用圆规和直尺(不量长度)你能作出线段AB垂直平分线吗?根据下面的做法试一试。
作法:(1)分别以点A、B为圆心,以大于1/2AB的长为半径画弧,两弧相交于点C、D;
(2)作直线CD
所以直线CD就是AB垂直平分线,也是线段AB的对称轴。
问:这样所作的直线为什么是线段的垂直平分线?
6、课本P64练习题1、2
三、课堂展示
例1、试着画出下边两个轴对称图形的对称轴。
例2、下面是我们学过的一些几何图形,说出下面图形是不是轴对称图形,并完成下表。
长方形 正方形 三角形 等腰三角形 等边三角形
平行四边形 任意梯形 等腰梯形 圆
图
形
长方
形
正方
形
三角
形
等腰
三角
形
等边
三角
形
平行
四边
形
任意
梯形
等腰
梯形
圆
对称轴的条数
三、随堂练习
1、画出以下图形的对称轴
2、课本P64练习题3
3、课本P65习题5
13.2 画轴对称图形
学习目标
1.能够按要求作出简单平面图形经过一次对称后的图形。
2、能设计简单的轴对称图案。
3、通过画轴对称图形,增强学生学习几何的趣味感,培养审美情操。:
重点:利用对称轴作轴对称图形。
难点:利用对称轴进行图案设计。
教学过程
一、预习新知P39---P41
1、如图:你能做出它关于虚线的对称图形吗?
(1)找到点A的对称点A′
(2) A A′与对称轴有什么关系?
(3)在图中另找一对对称点,连接对称点的线段与对称轴还
有上述关系吗?
2、连接任意一对对称点的线段被对称轴____________
3、如图,已知点A和直线l,试画出点A关于直线l的对称点A′。请说说你的画法
l
A·
作△ABC关于直线l的对称的图形△A′B′C′
5、课本P68练习题1
二、课堂展示
例1、已知△ABC,及点A的对称点A′,请作出对称轴直线l,并画出△ABC关于直线l的对称图形。
A . A′
B
C
随堂练习
1.如图,请画出三角形关于直线l对称的图形。
2、身高1.80米的人站在平面镜前2米处,它在镜子中的像高______米,人与像之间距离为_______米;如果他向前走0.2米,人与像之间距离为_________米.
3、P71习题1
4、为了美化环境,在一块正方形空地上分别种植四种不同的花草.现将这块空地按下列要求分成四块:⑴分割后的整个图形必须是轴对称图形;⑵四块图形形状相同;⑶四块图形面积相等.现已有两种不同的分法:⑴分别作两条对角线(如图中的图1);⑵过一条边的四等分点作这边的垂线段(图2)(图2中两个图形的分割看作同一方法).请你按照上述三个要求,分别在下面两个正方形中给出另外两种不同的分割方法.(正确画图,不写画法)
13.2用坐标表示轴对称
学习目标: 1、掌握在平面直角坐标系中,关于x轴和y轴对称点的坐标特点。
2、能在平面直角坐标系中画出一些简单的关于x轴和y轴的对称图形。
3、能运用坐标中的轴对称特点解决简单的问题。
重点:在平面直角坐标系中画出一些简单的关于x轴和y轴的对称图形。
难点:能运用坐标中的轴对称特点解决简单的问题。
一、预习新知P69-P70
1、如图,在平面直角坐标系中,
1)分别写出点A、B、C的坐标。
2)在坐标系中标出点A、B、C关于x轴的对称点
A1 、 B1、C1、。
3)写出A1 、 B1、C1、的坐标。
4)观察每对对称点的坐标,你发现了什么规律?
5)再找几个点,分别作出它们关于x轴的对称点,
检验一下你发现的规律。
由此可以得到:
在平面直角坐标系中,关于x轴对称的点横坐标_____,,纵坐标_________________。
点(x,y)关于x轴的对称点的坐标为__________.
2、如上图,在平面直角坐标系中,
1)在坐标系中标出点A、B、C关于关于y轴的对称点A2、B2、C2。
2)写出A2、B2、C2的坐标。
4)观察每对对称点的坐标,你发现了什么规律?
5)再找几个点,分别作出它们关于y轴的对称点,检验一下你发现的规律。
由此可以得到:
在平面直角坐标系中,关于y轴对称的点横坐标_____,,纵坐标_________________。
点(x,y)关于y轴的对称点的坐标为__________.
3、完成下表.
已知点
(2,-3)
(-1,2)
(-6,-5)
(0,-1.6)
(4,0)
关于x轴的对称点
?
?
?
?
?
关于y轴的对称点
?
?
?
?
?
4、点(-1,3)与点(-1,—3)关于_________对称;
点(2,—4)与点(-2,—4)关于_________对称;
5、已知△ABC的三个顶点的坐标分别为A(-3,5),B(- 4,1),C(-1,3),作出△ABC关于y轴对称的图形。 6、课本P70练习题1、2
二、课堂展示
例1、已知点P(2a+b,-3a)与点P’(8,b+2).
若点p与点p’关于x轴对称,则a=_____ b=_______.
若点p与点p’关于y轴对称,则a=_____ b=_______.
例2、平面直角坐标系中,△ABC的三个顶点坐标分别为A(0,4),B(2,4),C(3,-1).
(1)试在平面直角坐标系中,标出A、B、C三点;
(2)求△ABC的面积.
(3)若与△ABC关于x轴对称,写出、、的坐标.
三、随堂练习
1、快速口答
点(3,6)、(-7,9)关于x轴的对称点分别是什么?
点(-3,-5)、(0,10)关于y轴的对称点分别是什么?
2、根据下列点的坐标的变化,判断它们进
行了怎样的变换:
⑴ (-1,3) (-1,-3) ⑵ (-5,-4) (-5,4)
⑶ (3,4) (-3,4) ⑷ (1,0) (-1,0)
3、点M (a, -5)与点N(-2, b)关于y轴对称,则a=_____, b =_____.
4、课本P70习题2、3
5、已知点(x,4-y)与点(1-y,2x)关于y轴对称,则xy= ————————。
6、课本P72练习题5
7、已知A、B两点的坐标分别是(-2,3)和(2,3),则下面四个结论:①A、B关于x轴对称;②A、B关于y轴对称;③A、B关于原点对称;④若A、B之间的距离为4,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
8、已知A(-1,-2)和B(1,3),将点A向______平移________个单位长度后得到的点与点B关于y轴对称.
13.3.1 等腰三角形
学习目标
掌握等腰三角形的性质1、2
会利用等腰三角形的性质解决简单问题
自学指导
自学课本P75-P76内容,完成下列要求
认真学习探究的内容,边看边操作、思考
剪出的等腰三角形是否为轴对称图形
把剪出的等腰三角形沿折痕对折,找出其中重合的线段和角
认真学习等腰三角形性质的证明部分,注意辅助线的添加方法,体会能否可以添加底边上的高或顶角的平分线。
学习例1,体会等腰三角形性质的应用。
自学后完成展示内容,20分钟后进行展示。
展示内容
等腰三角形的两个底角_____,简写成_______
等腰三角形的顶角平分线____、_____相互重合。
已知△ABC中,AB=AC,AD⊥BC于D,求证:
(1)∠B=∠C (2)∠BAD=∠CAD (3)BD=CD
如图,在下列等腰三角形中,分别求出它们的底角的度数。
(2)
在△MNP中,MN = MO = OP,∠NMO = .求∠N和∠P
6、教材p81习题1,3,4
13.3.2等腰三角形
学习目标
掌握等腰三角形的判定方法
利用等腰三角形的判定方法
证明相关问题
辅助以尺规作图手段作等腰三角形
自学指导
自学课本77-78页内容,完成下列要求:
通过预习,思考77页内容后,你有哪些方法证明“等角对等边”这一结论?小组交流,互相探讨。
阅读例2,注意在证明一个三角形为等腰三角形时,关键就是找这个三角形中两条边相等或两角相等。
学习例3的内容,边看边操作,体会已知底边和底边上的高,用尺规作等腰三角形的方法。
自学20分钟后展示。
展示内容:
等腰三角形的判定方法:如果________,那么__________简写成“______”
已知△ABC中,∠B=∠C,求证:AB=AC
已知△ABC和BC上的高AD,BC=4cm,AD=3cm,求作等腰三角形ABC.
如左下图,∠A=, ∠C= ∠DBC=.分别计算∠BDC、∠ABD的度数,并说明图中有哪些等腰三角形。
如图(上右),AC和BD相交于O,且AB∥DC,OA=OB,
求证:OC=OD.
教材79页练习3
教材82页习题2,5,6
13.3.2 等边三角形(1)
一、自学目标
了解等边三角形的定义
掌握等边三角形的性质也判定
二、自学指导
认真阅读课本79-80页的内容,完成下列要求:
请你用等腰三角形的性质证明等边三角形的性质
在证明判定2时注意60°的角是等腰三角形的顶角或底角
合作交流例4的其它证法
自学后完成展示内容,20分钟后进行展示
三、展示内容
一个三角形一边的中线和高线重合,那么这个三角形是__
等腰三角形顶角的外角平分线与底边的位置关系是____
一个等腰三角形有三条对称轴,那么它就是___三角形。
在△ABC中,AB=AC,且∠A=60°,则△ABC是___三角形。
选择:下列叙述正确的是( )
A、等腰三角形是等边三角形 B、所有的等边三角形形状都相同,所以全等
C、三个角之比为1:2:3的三角形是等腰三角形
D、等边三角形的三条中线是它的三条对称轴
6、选择:如图在等边△ABC中,O为三条高线的交点,连结OB、OC那么∠BOC=( ) A、100° B、90°C、150° D、120°
证明:等边三角形的判定方法2.
8、O是等边三角形ABC内一点,∠OCB=∠ABO,求∠BOC的度数
9、等边三角形的三条中线交于一点,画出图中所有的全等三角形,并能说出它们是否全等?为什么?
13.3.2等边三角形(2)
学习目标
掌握含30°的直角三角形的对边与斜边的关系
能够证明这个关系
自学指导
1、认真阅读课本80-81页内容,按要求完成下列内容
探究部分的内容动手操作
合作探究其它的证明方法
学习例5
展示内容
填空:
RT△ABC中,∠C=90°,∠B=2∠A,则∠A=___,∠B=_____,AB=___BC
三角形的三个内角度数之比为1:2:3,最大边是8,则最小边为____
如图RT△ABC中,∠ABC=,BD⊥AB于D,且∠A=,BD=4cm,则BC=__
选择:
1、已知等腰三角形周长为40,以一腰为边作等边三角形,其周长为45,那么等腰三角形底边边长是( )
A、5 B、10 C、15 D、20
2、等腰△ABC中,∠A=,则∠B=( )
A、 B、 C、或 D、
3、已知等腰三角形两边长为7和3,则它的周长为( )
A、17 B、16 C、17或13 D、13
(三)解答
1、如图△ABC是等边三角形,AD为中线,AD=AE,求∠EDC的度数
2、△ABC为等边三角形,且DE⊥BC,垂足为D,EF⊥AC,垂足为E,FD⊥AB,垂足为F,则△DEF是等边三角形吗?这什么?
第十三章 轴对称复习导学案
学习目标:
1.理解轴对称与轴对称图形的概念,掌握轴对称的性质。
2.结合生活实例,欣赏生活中的轴对称现象和镜面对称现象,感受对称的美学价值,体验几何图形与自然、社会、人类的生活,增强学习数学的兴趣。
3.掌握线段的垂直平分线、角的平分线的性质及应用。
4.理解等腰三角形的性质并能够简单应用。
5.能够按要求做出简单的平面图形的轴对称图形,初步体会从对称的角度欣赏和设计简单的轴对称图案。
重点:掌握线段的垂直平分线、角的平分线的性质、等腰三角形的性质及应用。
难点:轴对称图形以及关于某条直线成轴对称的概念,等腰三角形的性质应用,镜面对称下图形的变化。
导学过程:
课前预习与导学
欣赏下面几张美丽的图片,回顾本单元的知识结构
1.轴对称图形:
如果一个图形沿着一条直线 ,两侧的图形能够 ,这个图形就是轴对称图形。折痕所在的这条直线叫做______。图形上能够重合的点叫 。
分别在上面图形中画出它们的对称轴。
2.轴对称:欣赏下面几幅图片,并完成问题。
如果把一个图形沿着某一条直线折叠后,能够与另一个图形重合,那么这两个图形关于这条直线成 ,这条直线叫做 。两个图形中的对应点叫 。如图,写出一对对称点是 。
3.轴对称的性质
上图中点A和F的连线与直线MN有什么样的关系?同理,点C和D,点B和E的连线也被直线MN ,图中相等的线段有:
,相等的角有: 。
可以概括为:如果两个图形关于某条直线成轴对称,那么对应点的连线被对称轴 ,对应线段 ,对应角 。
4.欣赏下面的图片,完成对镜面对称的回顾。
一辆汽车的车牌在水中的倒影如图所示,你能确定该车车牌的号码吗?
在照镜子时,镜子外的物体和镜子内的成像 不变,
发生相反变化。
5.线段垂直平分线的性质
线段垂直平分线上的点到 的距离相等。
6.角的平分线的性质
角的平分线的性质上的点到 的距离相等。
7.等腰三角形的性质
等腰三角形是 图形,它的对称轴是 ,
等腰三角形的两个底角 , 互相重合。
等边三角形的各角都是 ,有 条对称轴。
课上探究
激情导入:送一句话给全体同学
对称是一种思想,通过它,人们毕生追求,并创造次序、美丽和完善……
------赫尔曼·外尔
一、独立完成 发现问题(自主学习)
1.自主梳理
(一)轴对称和轴对称图形的联系和区别
区别:轴对称是两个图形能沿对称轴折叠后能重合,指的是 个图形的位置关系。
而轴对称图形是指 个图形的两部分沿对称轴折叠后能完全重合,指的是具有对称性的 个图形。
联系:
如果把成轴对称的两个图形看成一个整体,那么这个整体就是一个轴对称图形。
如果把一个轴对称图形位于对称轴两旁的部分看成两个图形,那么这两部分图形就成轴对称。
(二)线段垂直平分线的性质应用:三角形三边垂直平分线的交点到
距离相等。
(三)角的平分线的性质应用:三角形三个内角平分线的交点到 距离相等。
(四)等腰三角形的三线合一性是指: 。
2.自我诊断:
(1)下列说法中,正确的个数是( )
①轴对称图形只有一条对称轴,②轴对称图形的对称轴是一条线段,③两个图形成轴对称,这两个图形是全等图形,④全等的两个图形一定成轴对称,⑤轴对称图形是指一个图形,而轴对称是指两个图形而言。
(A)1个 (B)2个 (C)3个 (D)4个
(2)轴对称图形的对称轴的条数( )
(A)只有一条 (B)2条 (C)3条 (D)至少一条
(3)下列图形中,不是轴对称图形的是( )
(A)两条相交直线 (B)线段
(C)有公共端点的两条相等线段 (D)有公共端点的两条不相等线段
(4)下列图案是几种名车的标志,在这几个图案中是轴对称图形的共有( )
丰田 三菱 雪佛兰 雪铁龙
(A)1个 (B)2个 (C)3个 (D)4
(5)△ABC中,AB=AC,点D在AC边上,且 BD=BC=AD,则∠A的度数为( )
(A)300 (B)360 (C)450 (D)700
(6)等腰三角形两腰分别为3和7,那么它的周长为( )
(A)10 (B)13 (C)17 (D)13或17
(7)到三角形三个顶点距离相等的是( )
(A)三边高线的交点 (B)三条中线的交点
(C)三条垂直平分线的交点(D)三条内角平分线的交点
(8)等腰△ABC中∠A=80°,若∠A是顶角,则∠B=______°;若∠B是顶角,则∠B=_______°;若∠C是顶角,则∠B=________°
(9)小强站在镜前,从镜中看到镜子对面墙上挂着的电子表,
其读数如图所示,则电子表的实际时刻是__________。
(10)若△ABC与△A/B/C/关于直线MN对称,∠A=500,∠B/=700,则∠C/ =____。
自我总结:
你对以上问题感到还有疑惑的是: ,
是哪个知识点没有掌握好呢? 。
二、合作探究 解决问题
小组合作解决以下问题:
(1)画出△ABC关于直线l的轴对称图形△A`B`C`
(2)如图,A、B是安达公路边两个新建的居民小区,某镇需在公路边增加一个公共汽车站,这个公共汽车站建在什么位置,才能使两个小区到车站的路程一样,找出汽车站的位置并说明理由。
(3)数的运算中会有一些有趣的对称形式,如12×231=132×21,仿照这一形式,写出下列等式,并演算:12×462= ,18×891= 。
自我反思
在以上问题中,你对那个问题巩固的最扎实?那个问题你是接受了同学的帮助?你有哪些新的收获? 。
三、精讲点拨 完善问题
(1)在矩形ABCD中,将△ABC绕AC对折至△AEC
位置,CE与AD交于点F,如图.试说明EF=DF.
(2)如图,己知AB=AC,DE垂直平分AB交AC、AB
于D、E两点,若AB=12cm,BC=10cm,∠A=49o,
求△BCE的周长和∠EBC的度数.
我的收获:说明两条线段相等可以运用的方法主要是:
1. 2. 。
四、有效训练 归纳提升
(1)在△ABC中,AB=AC,BC=5cm,作AB的中垂线交另一腰AC于D,
连结BD,如果△BCD的周长是17cm,则腰长为( )
(A)12cm (B)6cm (C)7cm (D)5cm
(2)已知∠AOB=400,OM平分∠AOB,MA⊥OA于A,MB⊥OB于B,则∠MAB的度数为( )(A)500 (B)400 (C)300 (D)200
(3)△ABC中,BC=10,边BC的垂直平分线分别交AB、AC于点E、F,BE=7,△BCE的周长为_____。
(4)已知△ABC中∠BAC=140°,AB、AC的垂直平分线分别交BC于E、F,你能求出∠EAF的度数吗?
(5)在课外活动中,小明发明了一个在直角三角形中画锐角的平分线的方法,他的方法是:如图所示,在斜边AB上取一点E,使BE=BC,过点E作ED⊥AB,交AC于D,那么BD就是∠ABC的平分线,你认为对吗?为什么?
课末反思
本节课我的收获主要有:
我还在 方面存在不足,我打算 弥补。
课末检测
1.下列轴对称图形中,对称轴最多的是( )
(A)等腰直角三角形 (B)线段 (C)正方形 (D)圆
2.下列图形中不是轴对称图形的有( )
(A)1个 (B)2个 (C)3个 (D)4个
3.以下汽车标志中,和其他三个不同的是( )
(A) (B) (C) (D)
4.画出下图中△ABC关于直线MN的轴对称图形。
6.在Rt△ABC中,∠C=900,BD平分∠ABC交AC于点D,DE垂直平分线段AB,
①试找出图中相等的线段,并说明理由。②若DE=1cm,BD=2cm,求AC的长。
13.1.1 轴对称
学习目标
1、初步认识轴对称图形;判掌握关于某条直线成轴对称的两个图形的对应线段相等、对应角相等;
2、断一个图形是否是轴对称图形;理解轴对称图形和两个图形成轴对称这两个概念的区别与联系。
3、能够判别两个图形是否成轴对称。通过试验,归纳出轴对称图形概念,能用概念;培养良好的动手试验能力、归纳能力和语言表述能力。
重点:理解轴对称图形的概念;轴对称图形的对应线段相等、对应角相等
难点:判断图形是否是轴对称图形;两个图形成轴对称与轴对称图形两个概念的区别与联系。
一、预习新知P58
1、观察课本中的7副图片,你能找出它们的共同特征吗?
2、你能列举出一些现实生活中具有这种特征的物体和建筑物吗?
3、动手做一做:把一张纸对折,然后从折叠处剪出一个图形,展开后会是一个什么样的图形?它有什么特征?
4、如果一个图形沿一条__________折叠,________两旁的部分能够完全________.这个图形就叫做轴对称图形,这条________就是它的对称轴,这时,我们也说这个图形关于这条_________(成轴) 对称.
5、观察课本P59图13.1-3中的三幅图形,并试着沿虚线折叠,每对图形有什么共同特征?
6、一个图形沿着某条直线折叠,如果他能够与________重合,那么就说_______关于这条直线对称,这条直线叫做__________,折叠后________叫做对称点.
7、在课本中的图13.1-3的第三个图中,
(1)标出A、B、C的对称点,∠A、∠B、∠C的对应角,
(2)连接AA′,BB′,CC′,你发现这三条线段有什么关系?你找到规律了吗?
8、成轴对称的两个图形全等吗?为什么?
9、全等的两个图形成轴对称吗?试举例说明。(可以画图说明)
10、课本P60练习题
做下面的题,检验你预习的结果
1、轴对称图形的对称轴是一条___________
A直线 B射线 C线段
右面的图形是轴对称图形吗?如果是,指出对称轴。
二、课堂展示
1、我国的文字非常讲究对称美,分析图中的四个图案,图案( )有别于其余三个图案.
2、如图是我国几家银行的标志,在这几个图案中是轴对称图形的有哪些?它们各有几条对称轴,你能画出来吗?(小组讨论完成)
3、李芳同学球衣上的号码是253,当他把镜子放在号码的正左边时,镜子中的号码是( )
4、观察规律并填空:
5、参照下图说明轴对称图形与两个图形成轴对称有什么区别与联系?
(小组讨论回答)
三、随堂练习
1、课本P64习题1、2、3
2、下面哪些选项的右边图形与左边图形成轴对称?
3、如图,若沿虚线对折,左边部分与右边部分重合,请找出图中A、B、C的对称点,并说出图中有哪些角相等?哪些线段相等?
4、找出英文26个大写字母中哪些是轴对称图形?
5、你能举出三个是轴对称图形的汉字吗?
6、你能运用学过的知识把下面这个数学中不可能的式子变为可能吗?
7、如图,四边形ABCD与四边形EFGH关于MN对称。
(1)A、B、C、D的对称点分别是 ,线段AC、AB的对应线段分别是 ,CD= , ∠CBA= ,∠ADC= .
(2)AE与BF平行吗?为什么?
(3)AE与BF平行,能说明轴对称图形对称点的连线一定互相平行吗?
(4)延长线段BC、FG,交于点P,延长线段AB、EF,交于点Q,,你有什么发现吗?
13.1.2线段的垂直平分线1
学习目标:
通过动手试验掌握线段的垂直平分线的定义
理解线段垂直平分线与对称轴的关系
掌握线段垂直平分线的性质
重点:线段垂直平分线上的点到线段两端的距离相等。
难点:运用线段垂直平分线性质解决问题。
教学过程
一、预习新知P61
1、线段是轴对称图形吗?通过折叠的方法作出线段AB的对称轴l,交AB与O
1)点A的对称点是_______
2)量出AO与BO的长度,它们有什么关系?
3)AB与直线l在位置上有什么关系?
2、经过线段________并且______于这条线段的________,叫做这条线段的垂直平分线.
3、观察课本P59思考中的图,线段AA′,BB′,CC′与直线MN的关系是________
由上可得:对称轴与对应点所连线段的垂直平分线有什么关系?
已知直线l垂直平分线段AB,交AB与O.点C是l上任意一点,连接AC,BC.
量出AC,BC的长度,它们有什么关系?
另在l上任找一点D,量出AD,DB的长度,它们有什么关系?
由1),2),你得到什么猜想?
4)用我们以前学过的只是证明你的猜想。
6、线段垂直平分线上的点与这条线段两个端点的__________。
7、.课本P62练习题1.
二、课堂展示
例1、已知互不平行的两条线段AB, A′B′关于直线l对称,AB, A′B′所在的直线交于点P,判断下列正误。
1)AB=A′B′( ) 2)点P在直线l上( )
3)若A, A′是对称点,则l垂直平分线段A A′( )
4)若B, B′是对称点,则PB=P B′( )
例2.如右图所示,△ABC中,BC=10,边BC的垂直平分线分别交AB、BC于点E、D,BE=6,求△BCE的周长。
三、随堂练习
1.如右图所示,直线MN和DE分别是线段 AB、BC的垂直平分线,它们交于P点,请问PA和 PC相等吗?为什么?
2、如图,△ABC中,AB=AC=18cm,BC= 10cm,AB的垂直平分线ED交AC于D点,求:△BCD的周长。
13.1.2 线段的垂直平分线2
学习目标:
进一步理解线段垂直平分线的性质,并能灵活运用。
掌握线段垂直平分线的判定
运用线段垂直平分线的判定解决问题
重点:探索并理解线段垂直平分线的判定
难点:运用线段垂直平分线的判定解决问题
一、预习新知P61
1、用一根木棒和一根弹性均匀的橡皮筋,做一个简易的弓,箭通过木棒中央的孔射出去。
(1) (2)
1)如图(1)要使CO垂直于AB,需要添加什么条件?为什么?
那么点C在_____________上。
2)如图(2),拉动C,到达D的位置,若AD=DB,那么点D在__________上。
3)由1),2),你得到什么猜想?
4)用学过的知识证明你的猜想。
2、与一条线段两个端点距离________的点,在这条线段的______________上。
3、课本P62练习题2
二、课堂展示
例、如图所示,已知Rt△ABC中,∠C=90°,沿过B点的一条直线BE折叠这个三角形,使C点落在AB边上的点D.要使点D恰为AB的中点,问还要添加什么条件?根据你添加的条件,你能证明出D为AB的中点吗?
三、随堂练习
1、如图:已知直线l和l异侧的两点A、B,在直线l上求作一点P,使PA=PB.
2、 如图:已知,OD=OC,ED=EC,那么直线OE是线段
CD的______________,你能写出证明过程吗/
3、已知:E是∠AOB的平分线上一点,EC⊥OA ,ED⊥OB ,垂足分别为C、D.
求证:(1)∠ECD=∠EDC ;(2)OE是CD的垂直平分线.
轴对称
学习目标:
掌握用“连结对称点的线段被对称轴垂直平分”
熟练画出轴对称图形的对称轴。
3、培养良好的动手实践能力。
重点:验证一个图形是不是轴对称图形
难点:画轴对称图形的对称轴。
一、预习新知P62—P63
1、如图:不通过折叠的方法,你能验证出这两个四边形是否关于直线MN对称吗?
2、设A、B两点关于直线MN对称,则______垂直平分________.
3、轴对称图形的对称轴与对应点所连线段的垂直平分线有什么关系?
4、作轴对称图形的对称轴就是做作出一对对应点所连线段_____________
5、只用圆规和直尺(不量长度)你能作出线段AB垂直平分线吗?根据下面的做法试一试。
作法:(1)分别以点A、B为圆心,以大于1/2AB的长为半径画弧,两弧相交于点C、D;
(2)作直线CD
所以直线CD就是AB垂直平分线,也是线段AB的对称轴。
问:这样所作的直线为什么是线段的垂直平分线?
6、课本P64练习题1、2
三、课堂展示
例1、试着画出下边两个轴对称图形的对称轴。
例2、下面是我们学过的一些几何图形,说出下面图形是不是轴对称图形,并完成下表。
长方形 正方形 三角形 等腰三角形 等边三角形
平行四边形 任意梯形 等腰梯形 圆
图
形
长方
形
正方
形
三角
形
等腰
三角
形
等边
三角
形
平行
四边
形
任意
梯形
等腰
梯形
圆
对称轴的条数
三、随堂练习
1、画出以下图形的对称轴
2、课本P64练习题3
3、课本P65习题5
13.2 画轴对称图形
学习目标
1.能够按要求作出简单平面图形经过一次对称后的图形。
2、能设计简单的轴对称图案。
3、通过画轴对称图形,增强学生学习几何的趣味感,培养审美情操。:
重点:利用对称轴作轴对称图形。
难点:利用对称轴进行图案设计。
教学过程
一、预习新知P39---P41
1、如图:你能做出它关于虚线的对称图形吗?
(1)找到点A的对称点A′
(2) A A′与对称轴有什么关系?
(3)在图中另找一对对称点,连接对称点的线段与对称轴还
有上述关系吗?
2、连接任意一对对称点的线段被对称轴____________
3、如图,已知点A和直线l,试画出点A关于直线l的对称点A′。请说说你的画法
l
A·
作△ABC关于直线l的对称的图形△A′B′C′
5、课本P68练习题1
二、课堂展示
例1、已知△ABC,及点A的对称点A′,请作出对称轴直线l,并画出△ABC关于直线l的对称图形。
A . A′
B
C
随堂练习
1.如图,请画出三角形关于直线l对称的图形。
2、身高1.80米的人站在平面镜前2米处,它在镜子中的像高______米,人与像之间距离为_______米;如果他向前走0.2米,人与像之间距离为_________米.
3、P71习题1
4、为了美化环境,在一块正方形空地上分别种植四种不同的花草.现将这块空地按下列要求分成四块:⑴分割后的整个图形必须是轴对称图形;⑵四块图形形状相同;⑶四块图形面积相等.现已有两种不同的分法:⑴分别作两条对角线(如图中的图1);⑵过一条边的四等分点作这边的垂线段(图2)(图2中两个图形的分割看作同一方法).请你按照上述三个要求,分别在下面两个正方形中给出另外两种不同的分割方法.(正确画图,不写画法)
13.2用坐标表示轴对称
学习目标: 1、掌握在平面直角坐标系中,关于x轴和y轴对称点的坐标特点。
2、能在平面直角坐标系中画出一些简单的关于x轴和y轴的对称图形。
3、能运用坐标中的轴对称特点解决简单的问题。
重点:在平面直角坐标系中画出一些简单的关于x轴和y轴的对称图形。
难点:能运用坐标中的轴对称特点解决简单的问题。
一、预习新知P69-P70
1、如图,在平面直角坐标系中,
1)分别写出点A、B、C的坐标。
2)在坐标系中标出点A、B、C关于x轴的对称点
A1 、 B1、C1、。
3)写出A1 、 B1、C1、的坐标。
4)观察每对对称点的坐标,你发现了什么规律?
5)再找几个点,分别作出它们关于x轴的对称点,
检验一下你发现的规律。
由此可以得到:
在平面直角坐标系中,关于x轴对称的点横坐标_____,,纵坐标_________________。
点(x,y)关于x轴的对称点的坐标为__________.
2、如上图,在平面直角坐标系中,
1)在坐标系中标出点A、B、C关于关于y轴的对称点A2、B2、C2。
2)写出A2、B2、C2的坐标。
4)观察每对对称点的坐标,你发现了什么规律?
5)再找几个点,分别作出它们关于y轴的对称点,检验一下你发现的规律。
由此可以得到:
在平面直角坐标系中,关于y轴对称的点横坐标_____,,纵坐标_________________。
点(x,y)关于y轴的对称点的坐标为__________.
3、完成下表.
已知点
(2,-3)
(-1,2)
(-6,-5)
(0,-1.6)
(4,0)
关于x轴的对称点
?
?
?
?
?
关于y轴的对称点
?
?
?
?
?
4、点(-1,3)与点(-1,—3)关于_________对称;
点(2,—4)与点(-2,—4)关于_________对称;
5、已知△ABC的三个顶点的坐标分别为A(-3,5),B(- 4,1),C(-1,3),作出△ABC关于y轴对称的图形。 6、课本P70练习题1、2
二、课堂展示
例1、已知点P(2a+b,-3a)与点P’(8,b+2).
若点p与点p’关于x轴对称,则a=_____ b=_______.
若点p与点p’关于y轴对称,则a=_____ b=_______.
例2、平面直角坐标系中,△ABC的三个顶点坐标分别为A(0,4),B(2,4),C(3,-1).
(1)试在平面直角坐标系中,标出A、B、C三点;
(2)求△ABC的面积.
(3)若与△ABC关于x轴对称,写出、、的坐标.
三、随堂练习
1、快速口答
点(3,6)、(-7,9)关于x轴的对称点分别是什么?
点(-3,-5)、(0,10)关于y轴的对称点分别是什么?
2、根据下列点的坐标的变化,判断它们进
行了怎样的变换:
⑴ (-1,3) (-1,-3) ⑵ (-5,-4) (-5,4)
⑶ (3,4) (-3,4) ⑷ (1,0) (-1,0)
3、点M (a, -5)与点N(-2, b)关于y轴对称,则a=_____, b =_____.
4、课本P70习题2、3
5、已知点(x,4-y)与点(1-y,2x)关于y轴对称,则xy= ————————。
6、课本P72练习题5
7、已知A、B两点的坐标分别是(-2,3)和(2,3),则下面四个结论:①A、B关于x轴对称;②A、B关于y轴对称;③A、B关于原点对称;④若A、B之间的距离为4,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
8、已知A(-1,-2)和B(1,3),将点A向______平移________个单位长度后得到的点与点B关于y轴对称.
13.3.1 等腰三角形
学习目标
掌握等腰三角形的性质1、2
会利用等腰三角形的性质解决简单问题
自学指导
自学课本P75-P76内容,完成下列要求
认真学习探究的内容,边看边操作、思考
剪出的等腰三角形是否为轴对称图形
把剪出的等腰三角形沿折痕对折,找出其中重合的线段和角
认真学习等腰三角形性质的证明部分,注意辅助线的添加方法,体会能否可以添加底边上的高或顶角的平分线。
学习例1,体会等腰三角形性质的应用。
自学后完成展示内容,20分钟后进行展示。
展示内容
等腰三角形的两个底角_____,简写成_______
等腰三角形的顶角平分线____、_____相互重合。
已知△ABC中,AB=AC,AD⊥BC于D,求证:
(1)∠B=∠C (2)∠BAD=∠CAD (3)BD=CD
如图,在下列等腰三角形中,分别求出它们的底角的度数。
(2)
在△MNP中,MN = MO = OP,∠NMO = .求∠N和∠P
6、教材p81习题1,3,4
13.3.2等腰三角形
学习目标
掌握等腰三角形的判定方法
利用等腰三角形的判定方法
证明相关问题
辅助以尺规作图手段作等腰三角形
自学指导
自学课本77-78页内容,完成下列要求:
通过预习,思考77页内容后,你有哪些方法证明“等角对等边”这一结论?小组交流,互相探讨。
阅读例2,注意在证明一个三角形为等腰三角形时,关键就是找这个三角形中两条边相等或两角相等。
学习例3的内容,边看边操作,体会已知底边和底边上的高,用尺规作等腰三角形的方法。
自学20分钟后展示。
展示内容:
等腰三角形的判定方法:如果________,那么__________简写成“______”
已知△ABC中,∠B=∠C,求证:AB=AC
已知△ABC和BC上的高AD,BC=4cm,AD=3cm,求作等腰三角形ABC.
如左下图,∠A=, ∠C= ∠DBC=.分别计算∠BDC、∠ABD的度数,并说明图中有哪些等腰三角形。
如图(上右),AC和BD相交于O,且AB∥DC,OA=OB,
求证:OC=OD.
教材79页练习3
教材82页习题2,5,6
13.3.2 等边三角形(1)
一、自学目标
了解等边三角形的定义
掌握等边三角形的性质也判定
二、自学指导
认真阅读课本79-80页的内容,完成下列要求:
请你用等腰三角形的性质证明等边三角形的性质
在证明判定2时注意60°的角是等腰三角形的顶角或底角
合作交流例4的其它证法
自学后完成展示内容,20分钟后进行展示
三、展示内容
一个三角形一边的中线和高线重合,那么这个三角形是__
等腰三角形顶角的外角平分线与底边的位置关系是____
一个等腰三角形有三条对称轴,那么它就是___三角形。
在△ABC中,AB=AC,且∠A=60°,则△ABC是___三角形。
选择:下列叙述正确的是( )
A、等腰三角形是等边三角形 B、所有的等边三角形形状都相同,所以全等
C、三个角之比为1:2:3的三角形是等腰三角形
D、等边三角形的三条中线是它的三条对称轴
6、选择:如图在等边△ABC中,O为三条高线的交点,连结OB、OC那么∠BOC=( ) A、100° B、90°C、150° D、120°
证明:等边三角形的判定方法2.
8、O是等边三角形ABC内一点,∠OCB=∠ABO,求∠BOC的度数
9、等边三角形的三条中线交于一点,画出图中所有的全等三角形,并能说出它们是否全等?为什么?
13.3.2等边三角形(2)
学习目标
掌握含30°的直角三角形的对边与斜边的关系
能够证明这个关系
自学指导
1、认真阅读课本80-81页内容,按要求完成下列内容
探究部分的内容动手操作
合作探究其它的证明方法
学习例5
展示内容
填空:
RT△ABC中,∠C=90°,∠B=2∠A,则∠A=___,∠B=_____,AB=___BC
三角形的三个内角度数之比为1:2:3,最大边是8,则最小边为____
如图RT△ABC中,∠ABC=,BD⊥AB于D,且∠A=,BD=4cm,则BC=__
选择:
1、已知等腰三角形周长为40,以一腰为边作等边三角形,其周长为45,那么等腰三角形底边边长是( )
A、5 B、10 C、15 D、20
2、等腰△ABC中,∠A=,则∠B=( )
A、 B、 C、或 D、
3、已知等腰三角形两边长为7和3,则它的周长为( )
A、17 B、16 C、17或13 D、13
(三)解答
1、如图△ABC是等边三角形,AD为中线,AD=AE,求∠EDC的度数
2、△ABC为等边三角形,且DE⊥BC,垂足为D,EF⊥AC,垂足为E,FD⊥AB,垂足为F,则△DEF是等边三角形吗?这什么?
第十三章 轴对称复习导学案
学习目标:
1.理解轴对称与轴对称图形的概念,掌握轴对称的性质。
2.结合生活实例,欣赏生活中的轴对称现象和镜面对称现象,感受对称的美学价值,体验几何图形与自然、社会、人类的生活,增强学习数学的兴趣。
3.掌握线段的垂直平分线、角的平分线的性质及应用。
4.理解等腰三角形的性质并能够简单应用。
5.能够按要求做出简单的平面图形的轴对称图形,初步体会从对称的角度欣赏和设计简单的轴对称图案。
重点:掌握线段的垂直平分线、角的平分线的性质、等腰三角形的性质及应用。
难点:轴对称图形以及关于某条直线成轴对称的概念,等腰三角形的性质应用,镜面对称下图形的变化。
导学过程:
课前预习与导学
欣赏下面几张美丽的图片,回顾本单元的知识结构
1.轴对称图形:
如果一个图形沿着一条直线 ,两侧的图形能够 ,这个图形就是轴对称图形。折痕所在的这条直线叫做______。图形上能够重合的点叫 。
分别在上面图形中画出它们的对称轴。
2.轴对称:欣赏下面几幅图片,并完成问题。
如果把一个图形沿着某一条直线折叠后,能够与另一个图形重合,那么这两个图形关于这条直线成 ,这条直线叫做 。两个图形中的对应点叫 。如图,写出一对对称点是 。
3.轴对称的性质
上图中点A和F的连线与直线MN有什么样的关系?同理,点C和D,点B和E的连线也被直线MN ,图中相等的线段有:
,相等的角有: 。
可以概括为:如果两个图形关于某条直线成轴对称,那么对应点的连线被对称轴 ,对应线段 ,对应角 。
4.欣赏下面的图片,完成对镜面对称的回顾。
一辆汽车的车牌在水中的倒影如图所示,你能确定该车车牌的号码吗?
在照镜子时,镜子外的物体和镜子内的成像 不变,
发生相反变化。
5.线段垂直平分线的性质
线段垂直平分线上的点到 的距离相等。
6.角的平分线的性质
角的平分线的性质上的点到 的距离相等。
7.等腰三角形的性质
等腰三角形是 图形,它的对称轴是 ,
等腰三角形的两个底角 , 互相重合。
等边三角形的各角都是 ,有 条对称轴。
课上探究
激情导入:送一句话给全体同学
对称是一种思想,通过它,人们毕生追求,并创造次序、美丽和完善……
------赫尔曼·外尔
一、独立完成 发现问题(自主学习)
1.自主梳理
(一)轴对称和轴对称图形的联系和区别
区别:轴对称是两个图形能沿对称轴折叠后能重合,指的是 个图形的位置关系。
而轴对称图形是指 个图形的两部分沿对称轴折叠后能完全重合,指的是具有对称性的 个图形。
联系:
如果把成轴对称的两个图形看成一个整体,那么这个整体就是一个轴对称图形。
如果把一个轴对称图形位于对称轴两旁的部分看成两个图形,那么这两部分图形就成轴对称。
(二)线段垂直平分线的性质应用:三角形三边垂直平分线的交点到
距离相等。
(三)角的平分线的性质应用:三角形三个内角平分线的交点到 距离相等。
(四)等腰三角形的三线合一性是指: 。
2.自我诊断:
(1)下列说法中,正确的个数是( )
①轴对称图形只有一条对称轴,②轴对称图形的对称轴是一条线段,③两个图形成轴对称,这两个图形是全等图形,④全等的两个图形一定成轴对称,⑤轴对称图形是指一个图形,而轴对称是指两个图形而言。
(A)1个 (B)2个 (C)3个 (D)4个
(2)轴对称图形的对称轴的条数( )
(A)只有一条 (B)2条 (C)3条 (D)至少一条
(3)下列图形中,不是轴对称图形的是( )
(A)两条相交直线 (B)线段
(C)有公共端点的两条相等线段 (D)有公共端点的两条不相等线段
(4)下列图案是几种名车的标志,在这几个图案中是轴对称图形的共有( )
丰田 三菱 雪佛兰 雪铁龙
(A)1个 (B)2个 (C)3个 (D)4
(5)△ABC中,AB=AC,点D在AC边上,且 BD=BC=AD,则∠A的度数为( )
(A)300 (B)360 (C)450 (D)700
(6)等腰三角形两腰分别为3和7,那么它的周长为( )
(A)10 (B)13 (C)17 (D)13或17
(7)到三角形三个顶点距离相等的是( )
(A)三边高线的交点 (B)三条中线的交点
(C)三条垂直平分线的交点(D)三条内角平分线的交点
(8)等腰△ABC中∠A=80°,若∠A是顶角,则∠B=______°;若∠B是顶角,则∠B=_______°;若∠C是顶角,则∠B=________°
(9)小强站在镜前,从镜中看到镜子对面墙上挂着的电子表,
其读数如图所示,则电子表的实际时刻是__________。
(10)若△ABC与△A/B/C/关于直线MN对称,∠A=500,∠B/=700,则∠C/ =____。
自我总结:
你对以上问题感到还有疑惑的是: ,
是哪个知识点没有掌握好呢? 。
二、合作探究 解决问题
小组合作解决以下问题:
(1)画出△ABC关于直线l的轴对称图形△A`B`C`
(2)如图,A、B是安达公路边两个新建的居民小区,某镇需在公路边增加一个公共汽车站,这个公共汽车站建在什么位置,才能使两个小区到车站的路程一样,找出汽车站的位置并说明理由。
(3)数的运算中会有一些有趣的对称形式,如12×231=132×21,仿照这一形式,写出下列等式,并演算:12×462= ,18×891= 。
自我反思
在以上问题中,你对那个问题巩固的最扎实?那个问题你是接受了同学的帮助?你有哪些新的收获? 。
三、精讲点拨 完善问题
(1)在矩形ABCD中,将△ABC绕AC对折至△AEC
位置,CE与AD交于点F,如图.试说明EF=DF.
(2)如图,己知AB=AC,DE垂直平分AB交AC、AB
于D、E两点,若AB=12cm,BC=10cm,∠A=49o,
求△BCE的周长和∠EBC的度数.
我的收获:说明两条线段相等可以运用的方法主要是:
1. 2. 。
四、有效训练 归纳提升
(1)在△ABC中,AB=AC,BC=5cm,作AB的中垂线交另一腰AC于D,
连结BD,如果△BCD的周长是17cm,则腰长为( )
(A)12cm (B)6cm (C)7cm (D)5cm
(2)已知∠AOB=400,OM平分∠AOB,MA⊥OA于A,MB⊥OB于B,则∠MAB的度数为( )(A)500 (B)400 (C)300 (D)200
(3)△ABC中,BC=10,边BC的垂直平分线分别交AB、AC于点E、F,BE=7,△BCE的周长为_____。
(4)已知△ABC中∠BAC=140°,AB、AC的垂直平分线分别交BC于E、F,你能求出∠EAF的度数吗?
(5)在课外活动中,小明发明了一个在直角三角形中画锐角的平分线的方法,他的方法是:如图所示,在斜边AB上取一点E,使BE=BC,过点E作ED⊥AB,交AC于D,那么BD就是∠ABC的平分线,你认为对吗?为什么?
课末反思
本节课我的收获主要有:
我还在 方面存在不足,我打算 弥补。
课末检测
1.下列轴对称图形中,对称轴最多的是( )
(A)等腰直角三角形 (B)线段 (C)正方形 (D)圆
2.下列图形中不是轴对称图形的有( )
(A)1个 (B)2个 (C)3个 (D)4个
3.以下汽车标志中,和其他三个不同的是( )
(A) (B) (C) (D)
4.画出下图中△ABC关于直线MN的轴对称图形。
6.在Rt△ABC中,∠C=900,BD平分∠ABC交AC于点D,DE垂直平分线段AB,
①试找出图中相等的线段,并说明理由。②若DE=1cm,BD=2cm,求AC的长。
