2022-2023学年人教版八年级数学上册 14.1.4 整式的乘法 课件(共16张)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册 14.1.4 整式的乘法 课件(共16张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-05 20:05:41 | ||
图片预览



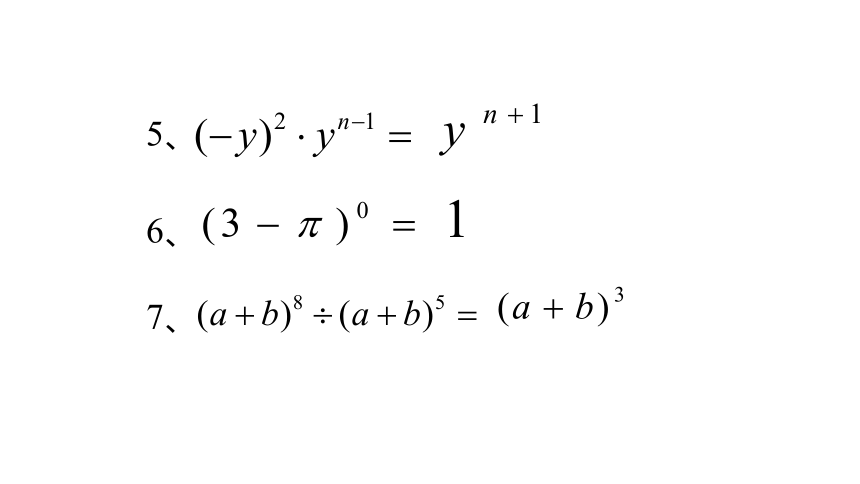



文档简介
(共16张PPT)
14.1.4 整式的乘法
计算下列各式并指出所用公式 的名称
同底数幂的乘法
幂的乘方
积的乘方
同底数幂的除法
零指数幂性质
负整数指数幂性质
一、复习回顾
抢 答
1、
2、
3、
4、
5、
6、
7、
单项式中的数字因数叫做这个单项式的__________
8、
9、
10、
系数
单项式 的系数是____
单项式 的系数是____
单项式与单项式相乘
一
问题1 光的速度约为3×105km/s,太阳光照射到地球上需要的时间大约是5×102s,你知道地球与太阳的距离约是多少吗
地球与太阳的距离约是(3×105)×(5×102)km
(3×105)×(5×102)
=(3×5)×(105×102)
=15×107.
乘法交换律、结合律
同底数幂的乘法
这种书写规范吗?
不规范,应为1.5×108.
思考:怎样计算(3 ×105)×(5 ×102)?计算过程中用到了哪些运算律及运算性质?
思考:如果将上式中的数字改为字母,比如ac5 ·bc2,怎样计算这个式子?
根据以上计算,想一想如何计算单项式乘以单项式?
ac5 ·bc2
=(a ·b) ·(c5·c2) (乘法交换律、结合律)
=abc5+2 (同底数幂的乘法)
=abc7.
知识要点
单项式与单项式的乘法法则
单项式与单项式相乘,把它们的系数、同底数幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
acm ·bcn=(a ·b) ·(cm·cn)
=abcm+n
典例精析
例1 计算:
(1) (-5a2b)(-3a); (2) (2x)3(-5xy3).
解:(1) (-5a2b)(-3a)
= [(-5)×(-3)](a2 a)b
= 15a3b;
解: 原式 =8x3(-5xy3)
=[8×(-5)](x3 x)y3
=-40x4y3.
单项式与单项式相乘
有理数的乘法与同底数幂的乘法
乘法交换律和结合律
转化
单项式乘以多项式的法则:
单项式与多项式相乘,就是用单项式去乘多项式的
每一项,再把所得的积相加.
探索法则
请你用自己的语言概括单项式乘以多项式的法则.
练习1 下列计算对吗?若不对,应该怎样改?
(1)
(2)
(3)
(4)
试一试
巩固法则
例1 计算:
(1)
(2)
巩固法则
练习2 计算下列各式:
(1)
(2)
(3)
(4)
巩固提高
练习3 化简:
(1)
(2)
几点注意:
1.单项式乘多项式的结果仍是多项式,积的项数与原多项式的项数相同。
2.在单项式乘法运算中要注意系数的符号。
3.不要出现漏乘现象,运算要有顺序。
14.1.4 整式的乘法
计算下列各式并指出所用公式 的名称
同底数幂的乘法
幂的乘方
积的乘方
同底数幂的除法
零指数幂性质
负整数指数幂性质
一、复习回顾
抢 答
1、
2、
3、
4、
5、
6、
7、
单项式中的数字因数叫做这个单项式的__________
8、
9、
10、
系数
单项式 的系数是____
单项式 的系数是____
单项式与单项式相乘
一
问题1 光的速度约为3×105km/s,太阳光照射到地球上需要的时间大约是5×102s,你知道地球与太阳的距离约是多少吗
地球与太阳的距离约是(3×105)×(5×102)km
(3×105)×(5×102)
=(3×5)×(105×102)
=15×107.
乘法交换律、结合律
同底数幂的乘法
这种书写规范吗?
不规范,应为1.5×108.
思考:怎样计算(3 ×105)×(5 ×102)?计算过程中用到了哪些运算律及运算性质?
思考:如果将上式中的数字改为字母,比如ac5 ·bc2,怎样计算这个式子?
根据以上计算,想一想如何计算单项式乘以单项式?
ac5 ·bc2
=(a ·b) ·(c5·c2) (乘法交换律、结合律)
=abc5+2 (同底数幂的乘法)
=abc7.
知识要点
单项式与单项式的乘法法则
单项式与单项式相乘,把它们的系数、同底数幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
acm ·bcn=(a ·b) ·(cm·cn)
=abcm+n
典例精析
例1 计算:
(1) (-5a2b)(-3a); (2) (2x)3(-5xy3).
解:(1) (-5a2b)(-3a)
= [(-5)×(-3)](a2 a)b
= 15a3b;
解: 原式 =8x3(-5xy3)
=[8×(-5)](x3 x)y3
=-40x4y3.
单项式与单项式相乘
有理数的乘法与同底数幂的乘法
乘法交换律和结合律
转化
单项式乘以多项式的法则:
单项式与多项式相乘,就是用单项式去乘多项式的
每一项,再把所得的积相加.
探索法则
请你用自己的语言概括单项式乘以多项式的法则.
练习1 下列计算对吗?若不对,应该怎样改?
(1)
(2)
(3)
(4)
试一试
巩固法则
例1 计算:
(1)
(2)
巩固法则
练习2 计算下列各式:
(1)
(2)
(3)
(4)
巩固提高
练习3 化简:
(1)
(2)
几点注意:
1.单项式乘多项式的结果仍是多项式,积的项数与原多项式的项数相同。
2.在单项式乘法运算中要注意系数的符号。
3.不要出现漏乘现象,运算要有顺序。
