2022-2023学年人教版八年级数学上册 14.2.2 完全平方公式 课件 (共15张)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册 14.2.2 完全平方公式 课件 (共15张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-05 20:07:00 | ||
图片预览



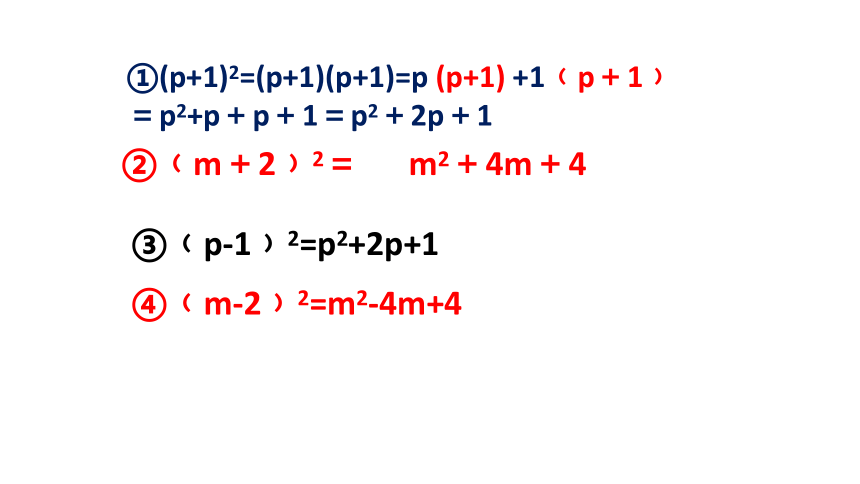

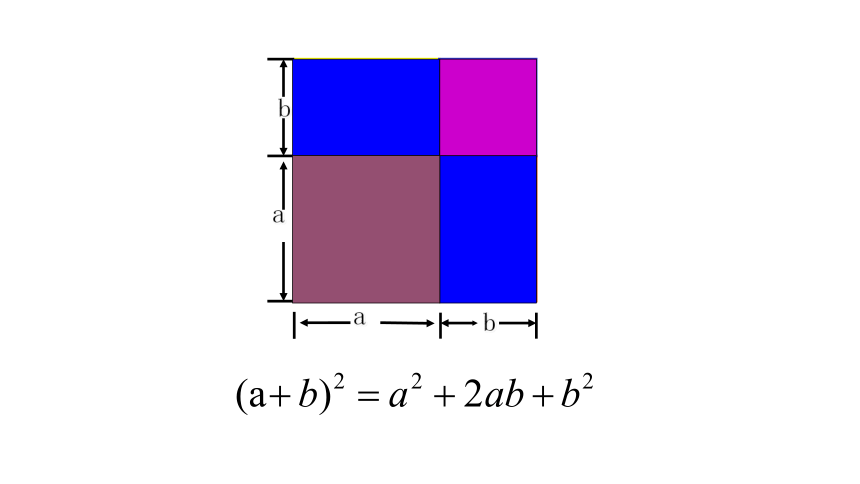
文档简介
(共15张PPT)
14.2.2 完全平方公式
(a+b)(a-b) = a2-b2
.
*平方差公式
判断*(2x+3)(3x-2)=6x2-6
2x(3x-2)+3(3x-2)=6x2-4x+9x-6=6x2-5x-6
一、复习引入
(× )
二、探求新知
像研究平方差公式一样,我们探究一下(a+b)2的运算结果有什么规律.
计算下列各式,你能发现什么规律?
(1)(p+1)2=(p+1)(p+1)=_______;
(2)(m+2)2=_______;
(3)(p-1)2=(p-1)(p-1)=________;
(4)(m-2)2=________;
①(p+1)2=(p+1)(p+1)=p (p+1) +1﹙p+1﹚=p2+p+p+1=p2+2p+1
②﹙m+2﹚2= m2+4m+4
③﹙p-1﹚2=p2+2p+1
④﹙m-2﹚2=m2-4m+4
计算下列各式,你能发现什么?
(p+1)2 =
(m+2)2=
(p-1)2 =
(m-2)2 =
p2+2p+1=p2+2×p×1+12
m2+4m+4=m2+2×m×2+22
p2-2p+1=p2-2×p×1+12
m2- 4m+4=m2-2×m×2+22
猜想 (a+b)2=
(a -b)2=
a2+2ab+b2
a2 - 2ab+b2
a
b
a
b
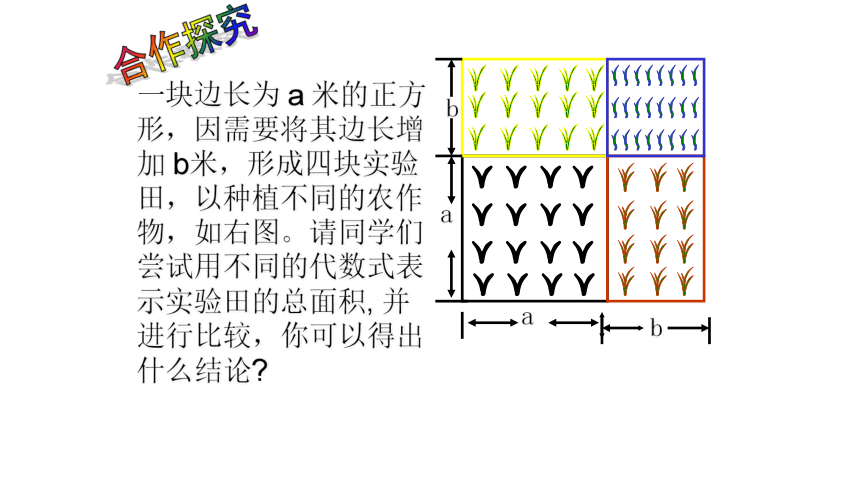
一块边长为 a 米的正方形,因需要将其边长增加 b米,形成四块实验田,以种植不同的农作物,如右图。请同学们尝试用不同的代数式表示实验田的总面积, 并进行比较,你可以得出什么结论
合作探究
a
b
a
b
2b
3a
3a
2b
合作探究
下面我们来猜想(a+b)2, (a-b)2的结果
(a+b)2=a2+2ab+b2. (a-b)2=a2-2ab+b2
探究完全平方公式
验证:(a+b)2=(a+b) (a+b) = a2+ab+ab+b2
=a2+2ab+b2.
(a-b)2 = (a-b) (a-b) = a2-ab-ab+b2
=a2-2ab+b2
一般地,我们有
即两数和(或差)的平方,等于它们的平方和,加(或减)它们的积的2倍.
这两个公式叫做(乘法的)完全平方公式.
(a+b)2=a2+2ab+b2,
(a-b) 2 = a2-2ab +b2.
探究完全平方公式
特点:首平方,尾平方,二倍乘积项在中央。
注意:a、b可以是数,单项式或多项式
例3 运用完全平方公式计算:
(1) (-3m+n)2; (2) (y- )2.
解: (1) (-3m+n) 2= (-3m)2 + 2 (-3m) n+n2
= 9m2-6mn +n2;
(2) (y - )2 = y2 - 2 y + ( )2
= y2-y +
运用完全平方公式
例4 运用完全平方公式计算:
(1) 1012 ; (2) 992 .
解: (1) 1022 = (100 +1) 2
= 1002 +2×100×1 + 12
= 10 000 +200 +1
= 10 201 .
(2) 982 = (100 -2)2
= 1002 -2×100×2+22
= 10 000 - 400 + 4
= 9 604.
(1) (p+q)2=p2+q2
(2) (a+2b)2=a2+4ab+2b2
(3) (a2+1)2=a4+2a+1
(4) (-s+t)2=s2-2st+t2
判断题
4
a2
( × )
( × )
( × )
( √ )
课堂练习
课堂小结
(a+b)2=a2+2ab+b2,
(a-b) 2 = a2-2ab +b2.
口诀:首平方,尾平方,积的2倍放中央
14.2.2 完全平方公式
(a+b)(a-b) = a2-b2
.
*平方差公式
判断*(2x+3)(3x-2)=6x2-6
2x(3x-2)+3(3x-2)=6x2-4x+9x-6=6x2-5x-6
一、复习引入
(× )
二、探求新知
像研究平方差公式一样,我们探究一下(a+b)2的运算结果有什么规律.
计算下列各式,你能发现什么规律?
(1)(p+1)2=(p+1)(p+1)=_______;
(2)(m+2)2=_______;
(3)(p-1)2=(p-1)(p-1)=________;
(4)(m-2)2=________;
①(p+1)2=(p+1)(p+1)=p (p+1) +1﹙p+1﹚=p2+p+p+1=p2+2p+1
②﹙m+2﹚2= m2+4m+4
③﹙p-1﹚2=p2+2p+1
④﹙m-2﹚2=m2-4m+4
计算下列各式,你能发现什么?
(p+1)2 =
(m+2)2=
(p-1)2 =
(m-2)2 =
p2+2p+1=p2+2×p×1+12
m2+4m+4=m2+2×m×2+22
p2-2p+1=p2-2×p×1+12
m2- 4m+4=m2-2×m×2+22
猜想 (a+b)2=
(a -b)2=
a2+2ab+b2
a2 - 2ab+b2
a
b
a
b
一块边长为 a 米的正方形,因需要将其边长增加 b米,形成四块实验田,以种植不同的农作物,如右图。请同学们尝试用不同的代数式表示实验田的总面积, 并进行比较,你可以得出什么结论
合作探究
a
b
a
b
2b
3a
3a
2b
合作探究
下面我们来猜想(a+b)2, (a-b)2的结果
(a+b)2=a2+2ab+b2. (a-b)2=a2-2ab+b2
探究完全平方公式
验证:(a+b)2=(a+b) (a+b) = a2+ab+ab+b2
=a2+2ab+b2.
(a-b)2 = (a-b) (a-b) = a2-ab-ab+b2
=a2-2ab+b2
一般地,我们有
即两数和(或差)的平方,等于它们的平方和,加(或减)它们的积的2倍.
这两个公式叫做(乘法的)完全平方公式.
(a+b)2=a2+2ab+b2,
(a-b) 2 = a2-2ab +b2.
探究完全平方公式
特点:首平方,尾平方,二倍乘积项在中央。
注意:a、b可以是数,单项式或多项式
例3 运用完全平方公式计算:
(1) (-3m+n)2; (2) (y- )2.
解: (1) (-3m+n) 2= (-3m)2 + 2 (-3m) n+n2
= 9m2-6mn +n2;
(2) (y - )2 = y2 - 2 y + ( )2
= y2-y +
运用完全平方公式
例4 运用完全平方公式计算:
(1) 1012 ; (2) 992 .
解: (1) 1022 = (100 +1) 2
= 1002 +2×100×1 + 12
= 10 000 +200 +1
= 10 201 .
(2) 982 = (100 -2)2
= 1002 -2×100×2+22
= 10 000 - 400 + 4
= 9 604.
(1) (p+q)2=p2+q2
(2) (a+2b)2=a2+4ab+2b2
(3) (a2+1)2=a4+2a+1
(4) (-s+t)2=s2-2st+t2
判断题
4
a2
( × )
( × )
( × )
( √ )
课堂练习
课堂小结
(a+b)2=a2+2ab+b2,
(a-b) 2 = a2-2ab +b2.
口诀:首平方,尾平方,积的2倍放中央
