2022-2023学年人教版八年级数学上册:14.2.1 平方差公式 课件 (共15张PPT)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册:14.2.1 平方差公式 课件 (共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-05 17:49:37 | ||
图片预览






文档简介
(共15张PPT)
14.2.1 平方差公式
(1)(x+1) (x-1)
(2)(m+2) (m-2)
(3)(2x+3) (2x-3)
(4)( y+4) ( y 4)
2
3
2
3
自
主
探
究
计算下列多项式的积:
= x2 - 1
= m2 - 4
= 4x2 - 9
y2 - 16
4
9
=
1.观察以上算式结构和计算结果你发现了什么规律?
2.能否用文字语言表达你发现的规律吗?
符号语言:
两个数的和与这两个数的差的积,等于这两个数的平方差.
文字语言:
总
结
规
律
平方差公式
合
作
探
究
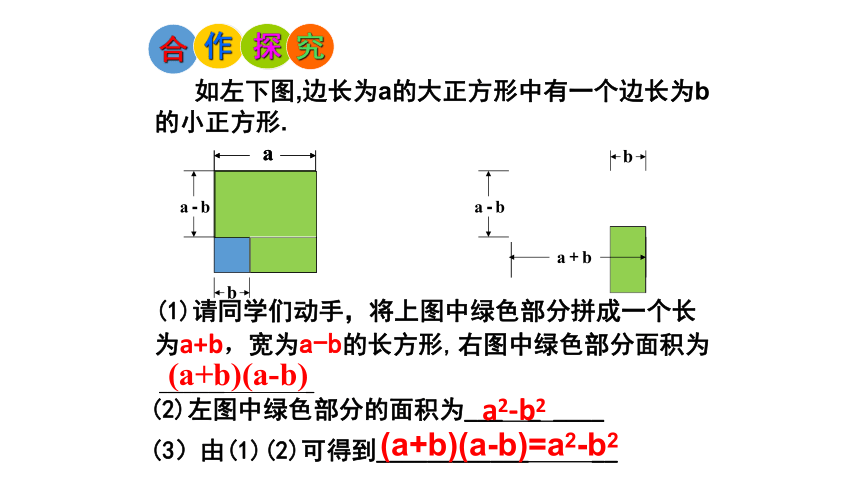
如左下图,边长为a的大正方形中有一个边长为b的小正方形.
(1)请同学们动手,将上图中绿色部分拼成一个长为a+b,宽为a-b的长方形,
(a+b)(a-b)
右图中绿色部分面积为
(2)左图中绿色部分的面积为___ _ ____
(3)由(1)(2)可得到____________ __
a2-b2
(a+b)(a-b)=a2-b2
________ _
( a + b )( a b ) = a2 b2
相同的项
“相反”的项
平方差公式
特征:
(相同的项)2-(相反的项)2
注意:公式中的a,b既可代表具体的数, 还可代表单项式或多项式。
(1+x)(1-x)
(-3+a)(-3-a)
(1+a)(-1+a)
a
b
a2-b2
结果
(a+b)(a-b)
1
x
12-x2
1-x2
-3
a
(-3)2-a2
9-a2
a
1
a2-12
a2-1
1、填一填
例1:运用平方差公式计算:
(1)
(2)
(-x+2y)(-x-2y)
(3x+2)( 3x-2 )
解: (3x+2)(3x-2)
(a+ b) ( a- b)
= a2 - b2
=(3x)2-22
= 9x2-4
解:原式=
(-x)2-(2y)2
= x2-4y2
应用中理解
典例分析
2.运用平方差公式计算.
(a+3b) (a-3b);
(2) (3+2a) (-3 + 2a) ;
练习
例2 利用平方差公式计算,看谁
算的对又快
(1)102×98
(2)51×49
解: (1)原式=(100+2)(100-2)
= 1002-22
=10 000 – 4
= 9 996.
解: (2)原式=(50+1)(50-1)
= 502-12
=2500 – 1
= 2499.
问题:李明一共买了4.2千克,正当售货员还在用计算器计算时,李明马上说出了共15.96元,售货员很惊奇地问:“你怎么算的这么快呢?真是一个速算王啊!”李明告诉她:这是一个秘密.
3.8元/kg
应用生活,答疑解难
知难而进
计算 20042 - 2003×2005;
解:
原式= 20042 - (2004-1)(2004+1)
= 20042
- (20042-12 )
= 20042
- 20042+12
=1
思维拓展,挑战自我
(1)(a+3b)(a - 3b)
(2)(3+2a)(-3+2a)
(4)(3x+4)(3x-4)-(2x+3)(3x-2)
计算下列各式
当堂检测
(3)51×49
利用平方差公式计算:
14.2.1 平方差公式
(1)(x+1) (x-1)
(2)(m+2) (m-2)
(3)(2x+3) (2x-3)
(4)( y+4) ( y 4)
2
3
2
3
自
主
探
究
计算下列多项式的积:
= x2 - 1
= m2 - 4
= 4x2 - 9
y2 - 16
4
9
=
1.观察以上算式结构和计算结果你发现了什么规律?
2.能否用文字语言表达你发现的规律吗?
符号语言:
两个数的和与这两个数的差的积,等于这两个数的平方差.
文字语言:
总
结
规
律
平方差公式
合
作
探
究
如左下图,边长为a的大正方形中有一个边长为b的小正方形.
(1)请同学们动手,将上图中绿色部分拼成一个长为a+b,宽为a-b的长方形,
(a+b)(a-b)
右图中绿色部分面积为
(2)左图中绿色部分的面积为___ _ ____
(3)由(1)(2)可得到____________ __
a2-b2
(a+b)(a-b)=a2-b2
________ _
( a + b )( a b ) = a2 b2
相同的项
“相反”的项
平方差公式
特征:
(相同的项)2-(相反的项)2
注意:公式中的a,b既可代表具体的数, 还可代表单项式或多项式。
(1+x)(1-x)
(-3+a)(-3-a)
(1+a)(-1+a)
a
b
a2-b2
结果
(a+b)(a-b)
1
x
12-x2
1-x2
-3
a
(-3)2-a2
9-a2
a
1
a2-12
a2-1
1、填一填
例1:运用平方差公式计算:
(1)
(2)
(-x+2y)(-x-2y)
(3x+2)( 3x-2 )
解: (3x+2)(3x-2)
(a+ b) ( a- b)
= a2 - b2
=(3x)2-22
= 9x2-4
解:原式=
(-x)2-(2y)2
= x2-4y2
应用中理解
典例分析
2.运用平方差公式计算.
(a+3b) (a-3b);
(2) (3+2a) (-3 + 2a) ;
练习
例2 利用平方差公式计算,看谁
算的对又快
(1)102×98
(2)51×49
解: (1)原式=(100+2)(100-2)
= 1002-22
=10 000 – 4
= 9 996.
解: (2)原式=(50+1)(50-1)
= 502-12
=2500 – 1
= 2499.
问题:李明一共买了4.2千克,正当售货员还在用计算器计算时,李明马上说出了共15.96元,售货员很惊奇地问:“你怎么算的这么快呢?真是一个速算王啊!”李明告诉她:这是一个秘密.
3.8元/kg
应用生活,答疑解难
知难而进
计算 20042 - 2003×2005;
解:
原式= 20042 - (2004-1)(2004+1)
= 20042
- (20042-12 )
= 20042
- 20042+12
=1
思维拓展,挑战自我
(1)(a+3b)(a - 3b)
(2)(3+2a)(-3+2a)
(4)(3x+4)(3x-4)-(2x+3)(3x-2)
计算下列各式
当堂检测
(3)51×49
利用平方差公式计算:
