2022-2023学年人教版八年级数学上册 14.3.1 提公因式法 课件 (共16张)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册 14.3.1 提公因式法 课件 (共16张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-05 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
14.3.1 提公因式法
因式分解定义
计算下列各式:
(1)7x(x-1)= _______
(2)c(ɑ+b-1)=__________
(3)(m+2)(m-2)= _______
根据左面的算式填空:
(1)7x2-7x=_________
(2)cɑ+cb-c=___________
(3)m2-4=____________
7x2-7x
cɑ+cb-c
m2-4
7x(x-1)
c(ɑ+b-1)
(m+2)(m-2)
像右面那样,把一个多项式化成几个整式的积的形式,叫做因式分解。
发散思维
思考:左边计算与右边计算之间有什么联系?
左边式子的变形为整式乘法,
右边式子的变形为因式分解,
两种变形互为逆运算。
小试牛刀:
下列由左边到右边的变形中,哪些是因式分解?
(1)x2+2x+1=(x+1)2( 是 )
(2)(x+3)(x-3)=x2-9 ( 否 )
(3)a2-b2=(a+b)(a-b)( 是 )
(4)bx2+by2=b(x2+y2) ( 是 )
提示:观察右边是否
是几个整式的积的形
式。
观察算式特点
用简便方法计算:
若算式包含字母呢
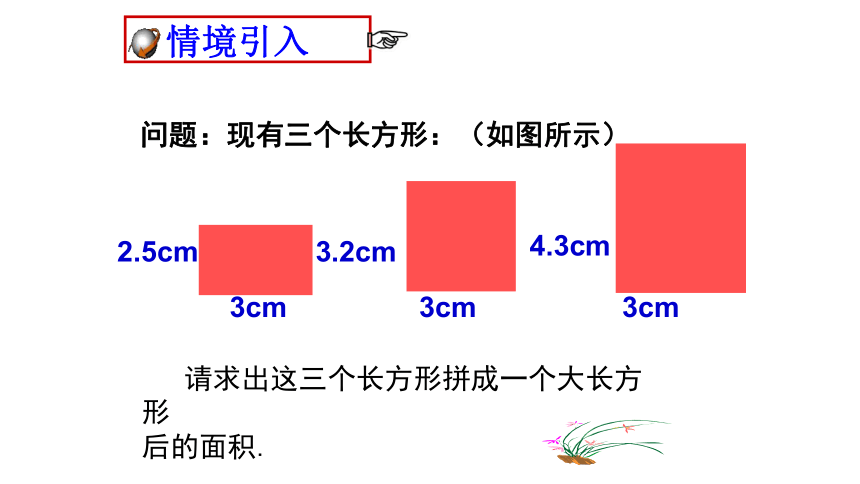
问题:现有三个长方形:(如图所示)
2.5cm
3.2cm
4.3cm
请求出这三个长方形拼成一个大长方形
后的面积.
3cm
3cm
3cm
情境引入
解法一:
3x2.5+3x3.2+3x4.3
解法二:
3 x(2.5+3.2+4.3)
3x2.5+3x3.2+3x4.3=3x(2.5+3.2+4.3)
无论是解法一还是解法二,求出的总面积都是相等的,所以有
公因式
xy+xz+xw=x(y+z+w)
几个多项式的公共的因式称为它们的公因式.
把3换成x,2.5换成y,3.2换成z,4.3换成w,则有
利用整式乘法验证,把乘法分配律从右到左地使用:
x(y+z+w)=xy+xz+xw.
合作探究
x x x x
6a3b2 -12ab3c 的公因式是什么?
一看系数 最大公约数
二看字母 相同字母
三看指数 最低指数
观察技巧
尝试因式分解
6a3b2 -12ab3c
=6ab2( a2 -2bc )
(1) 8a3b2 + 12ab3c
例1: 把下列各式分解因式
分析:提公因式法步骤(分两步)
第一步:找出公因式;
第二步:提取公因式 ,即将多项式化为两个因式的乘积.
(2) 2a(b+c) - 3(b+c)
注意:公因式既可以是一个单项式的形式,也可
以是一个多项式的形式
整体思想是数学中一种重要而且常用的思想方法.
小明解的有误吗?
把12x2y+18xy2分解因式
解:原式 =3xy(4x + 6y)
错误
公因式没有提尽,还可以提出公因式2
注意:公因式要提尽.
诊断
正确解:原式=6xy(2x+3y)
例2: 把 12b(a-b)2 – 18(b-a)2 分解因式
解: 12b(a-b)2 – 18(b-a)3
=12b(a-b)2 + 18(a-b)3
=6(a-b)2 [2b+3(a-b)]
=6(a-b)2 (2b+3a-3b)
=6(a-b)2(3a-b)
练习:(x-y)2+y(y-x)
(1) 13.8×0.125+86.2×1/8
(2)已知a+b=5,ab=3,求a2b+ab2的值.
解:原式=13.8×0.125+86.2×0.125
=0.125×(13.8+86.2)
=0.125×100
=12.5
解: a2b+ab2 =ab(a+b)=3 × 5=15
巧妙计算
说出下列多项式各项的公因式
练 习
1、正确找出多项式各项公因式的关键是:
公因式的系数是多项式各项系数的最大公约数.
字母取多项式各项中都含有的相同的字母.
相同字母的指数取各项中最小的一个,即字母最低次幂.
定系数:
定字母:
定指数:
归纳总结:
14.3.1 提公因式法
因式分解定义
计算下列各式:
(1)7x(x-1)= _______
(2)c(ɑ+b-1)=__________
(3)(m+2)(m-2)= _______
根据左面的算式填空:
(1)7x2-7x=_________
(2)cɑ+cb-c=___________
(3)m2-4=____________
7x2-7x
cɑ+cb-c
m2-4
7x(x-1)
c(ɑ+b-1)
(m+2)(m-2)
像右面那样,把一个多项式化成几个整式的积的形式,叫做因式分解。
发散思维
思考:左边计算与右边计算之间有什么联系?
左边式子的变形为整式乘法,
右边式子的变形为因式分解,
两种变形互为逆运算。
小试牛刀:
下列由左边到右边的变形中,哪些是因式分解?
(1)x2+2x+1=(x+1)2( 是 )
(2)(x+3)(x-3)=x2-9 ( 否 )
(3)a2-b2=(a+b)(a-b)( 是 )
(4)bx2+by2=b(x2+y2) ( 是 )
提示:观察右边是否
是几个整式的积的形
式。
观察算式特点
用简便方法计算:
若算式包含字母呢
问题:现有三个长方形:(如图所示)
2.5cm
3.2cm
4.3cm
请求出这三个长方形拼成一个大长方形
后的面积.
3cm
3cm
3cm
情境引入
解法一:
3x2.5+3x3.2+3x4.3
解法二:
3 x(2.5+3.2+4.3)
3x2.5+3x3.2+3x4.3=3x(2.5+3.2+4.3)
无论是解法一还是解法二,求出的总面积都是相等的,所以有
公因式
xy+xz+xw=x(y+z+w)
几个多项式的公共的因式称为它们的公因式.
把3换成x,2.5换成y,3.2换成z,4.3换成w,则有
利用整式乘法验证,把乘法分配律从右到左地使用:
x(y+z+w)=xy+xz+xw.
合作探究
x x x x
6a3b2 -12ab3c 的公因式是什么?
一看系数 最大公约数
二看字母 相同字母
三看指数 最低指数
观察技巧
尝试因式分解
6a3b2 -12ab3c
=6ab2( a2 -2bc )
(1) 8a3b2 + 12ab3c
例1: 把下列各式分解因式
分析:提公因式法步骤(分两步)
第一步:找出公因式;
第二步:提取公因式 ,即将多项式化为两个因式的乘积.
(2) 2a(b+c) - 3(b+c)
注意:公因式既可以是一个单项式的形式,也可
以是一个多项式的形式
整体思想是数学中一种重要而且常用的思想方法.
小明解的有误吗?
把12x2y+18xy2分解因式
解:原式 =3xy(4x + 6y)
错误
公因式没有提尽,还可以提出公因式2
注意:公因式要提尽.
诊断
正确解:原式=6xy(2x+3y)
例2: 把 12b(a-b)2 – 18(b-a)2 分解因式
解: 12b(a-b)2 – 18(b-a)3
=12b(a-b)2 + 18(a-b)3
=6(a-b)2 [2b+3(a-b)]
=6(a-b)2 (2b+3a-3b)
=6(a-b)2(3a-b)
练习:(x-y)2+y(y-x)
(1) 13.8×0.125+86.2×1/8
(2)已知a+b=5,ab=3,求a2b+ab2的值.
解:原式=13.8×0.125+86.2×0.125
=0.125×(13.8+86.2)
=0.125×100
=12.5
解: a2b+ab2 =ab(a+b)=3 × 5=15
巧妙计算
说出下列多项式各项的公因式
练 习
1、正确找出多项式各项公因式的关键是:
公因式的系数是多项式各项系数的最大公约数.
字母取多项式各项中都含有的相同的字母.
相同字母的指数取各项中最小的一个,即字母最低次幂.
定系数:
定字母:
定指数:
归纳总结:
