2022-2023学年人教版八年级数学上册 15.1.1 从分数到分式 课件(共15张)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册 15.1.1 从分数到分式 课件(共15张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-05 20:37:39 | ||
图片预览






文档简介
(共15张PPT)
15.1.1 从分数到分式
1.长方形的面积为10cm ,长为7cm,宽应为____cm;
2.长方形的面积为S,长为A,宽应为____;
3.把体积为200cm 的水倒入底面积为 33cm 的圆柱形容器中,水面高度为_____cm;
思考填空
4.把体积为V的水倒入底面积为S的圆柱形
容器中,水面高度为______.
5.一段绳子长3米,把它平均分成x+1份,则每份长是_______米.
思考填空
分式定义:
一般地,如果A、B表示两个整式,并且B中含有字母(未知数),那么称 为分式.
其中A叫做分式的分子,B为分式的分母.
注意:
1.分式是不同于整式的另一类式子,且分母中
含有字母(未知数),是分式的一大特点。
2 .分式比分数更具有一般性。
判断:下面的式子哪些是分式?
分式:
归纳:1.判断时,注意含有 的式子, 是常数.
2.式子中含有多项时,若其中有一项分
母含有字母,则该式也为分式,如:
.
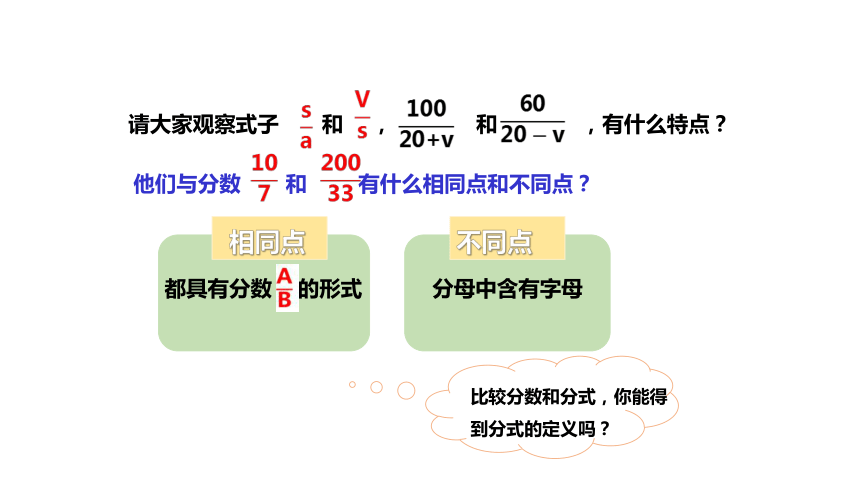
相同点
请大家观察式子 和 , 和 ,有什么特点?
他们与分数 和 有什么相同点和不同点?
都具有分数 的形式
不同点
分母中含有字母
比较分数和分式,你能得到分式的定义吗?
整数
整数
分数
整式A
整式B
(100-v)÷(20+v)
3 ÷ 5 =
被除数÷除数=商数
如:
被除式÷除式=商式
如:
分式
教学目标
分数
分式
比较分数和分式
=
请大家求下列分式的值,填表后请思考
1、什么情况下,值不存在?为什么?
探究分式有意义的条件
对于分式
当_______时分式有意义;
当_______时无意义.
B≠0
B=0
分式有意义的条件
(2) 当x为何值时,分式有意义
(1) 当x为何值时,分式无意义
(2)由(1)得 当x ≠-2时,分式有意义.
∴当x = -2时分式无意义.
解:(1)当分母等于零时,分式无意义.
∴ x =-2,
即 x+2=0
例1
提升自我运动
1.下列代数式中,属于分式的有( )
A. B. C. D.
C
2.当a=-1时,分式 的值( )
A.没有意义 B.等于零
C.等于1 D.等于-1
A
3.当x为任意实数时,下列分式一定有意义的是( )
A.
B.
C.
D.
B
4.已知,当x=5时,分式 的值等于零,则k .
=-10
5.在分式 中,当x为何值时,分式有意义?分式的值为零?
答:当x ≠ 3时,该分式有意义;当x=-3时,该分式的值为零.
闭幕式—课堂小结
分式
定义
值为零的条件
有(无)意义的条件
一般地,如果A,B表示整式,且B中含有字母,式子 叫做分式 ,其中,A叫做分式的分子,B叫做分式的分母.
分式 有意义的条件是B ≠0.
分式 有意义的条件是B =0.
分式 值为零的条件是A=0且B ≠0.
15.1.1 从分数到分式
1.长方形的面积为10cm ,长为7cm,宽应为____cm;
2.长方形的面积为S,长为A,宽应为____;
3.把体积为200cm 的水倒入底面积为 33cm 的圆柱形容器中,水面高度为_____cm;
思考填空
4.把体积为V的水倒入底面积为S的圆柱形
容器中,水面高度为______.
5.一段绳子长3米,把它平均分成x+1份,则每份长是_______米.
思考填空
分式定义:
一般地,如果A、B表示两个整式,并且B中含有字母(未知数),那么称 为分式.
其中A叫做分式的分子,B为分式的分母.
注意:
1.分式是不同于整式的另一类式子,且分母中
含有字母(未知数),是分式的一大特点。
2 .分式比分数更具有一般性。
判断:下面的式子哪些是分式?
分式:
归纳:1.判断时,注意含有 的式子, 是常数.
2.式子中含有多项时,若其中有一项分
母含有字母,则该式也为分式,如:
.
相同点
请大家观察式子 和 , 和 ,有什么特点?
他们与分数 和 有什么相同点和不同点?
都具有分数 的形式
不同点
分母中含有字母
比较分数和分式,你能得到分式的定义吗?
整数
整数
分数
整式A
整式B
(100-v)÷(20+v)
3 ÷ 5 =
被除数÷除数=商数
如:
被除式÷除式=商式
如:
分式
教学目标
分数
分式
比较分数和分式
=
请大家求下列分式的值,填表后请思考
1、什么情况下,值不存在?为什么?
探究分式有意义的条件
对于分式
当_______时分式有意义;
当_______时无意义.
B≠0
B=0
分式有意义的条件
(2) 当x为何值时,分式有意义
(1) 当x为何值时,分式无意义
(2)由(1)得 当x ≠-2时,分式有意义.
∴当x = -2时分式无意义.
解:(1)当分母等于零时,分式无意义.
∴ x =-2,
即 x+2=0
例1
提升自我运动
1.下列代数式中,属于分式的有( )
A. B. C. D.
C
2.当a=-1时,分式 的值( )
A.没有意义 B.等于零
C.等于1 D.等于-1
A
3.当x为任意实数时,下列分式一定有意义的是( )
A.
B.
C.
D.
B
4.已知,当x=5时,分式 的值等于零,则k .
=-10
5.在分式 中,当x为何值时,分式有意义?分式的值为零?
答:当x ≠ 3时,该分式有意义;当x=-3时,该分式的值为零.
闭幕式—课堂小结
分式
定义
值为零的条件
有(无)意义的条件
一般地,如果A,B表示整式,且B中含有字母,式子 叫做分式 ,其中,A叫做分式的分子,B叫做分式的分母.
分式 有意义的条件是B ≠0.
分式 有意义的条件是B =0.
分式 值为零的条件是A=0且B ≠0.
