2022-2023学年青岛版数学九年级上册 4.5一元二次方程的应用(1)课件 (共19张)
文档属性
| 名称 | 2022-2023学年青岛版数学九年级上册 4.5一元二次方程的应用(1)课件 (共19张) |  | |
| 格式 | zip | ||
| 文件大小 | 889.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-05 19:07:23 | ||
图片预览






文档简介
(共19张PPT)
4.7 一元二次方程的应用
青岛版 数学 九(上) 第四章: 一元二次方程
复习回顾
1、列方程(组)解应用题的方法步骤:
(1)审题:
(2)设未知数:
(3)列方程(组):
(4)解方程(组):
(5)检验:
(6)写答:
(找题目中的已知量、未知量、量与量的关
系及等量关系)
(间接设或直接设)
(根据量与量的关系及等量关系)
(验根是否是所列方程的解,且是否符合题意)
2、列方程(组)解应用题时的题型:
注意:各类型的题目还有各类型的独立关系式.
复习回顾
(1)行程问题:
(2)工程问题:
(4)图形的面积(或体积)问题:
(3)市场营销问题:
(5)银行存款问题:
(6)利率问题:
(7)数字问题;等等
同样,与我们学习过的一元一次方程、二元一次方程组和分式方程一样,一元二次方程也是刻画现实生活和生产中数量关系的有效模型.
例题讲解
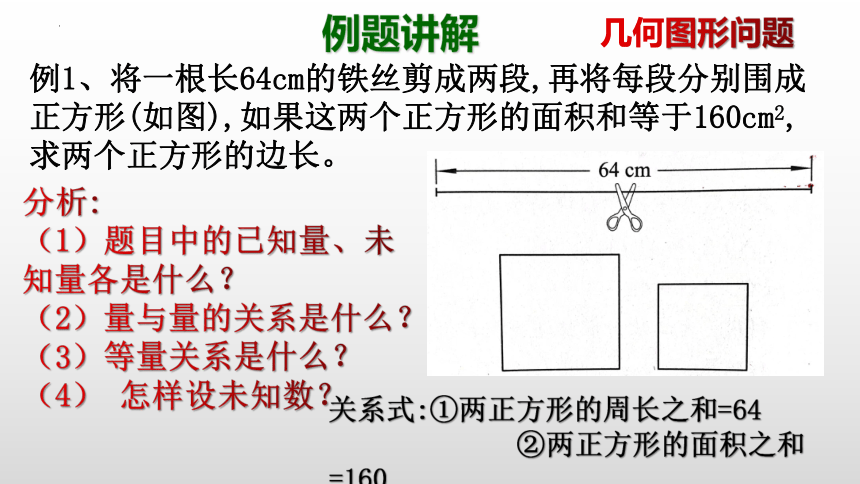
例1、将一根长64cm的铁丝剪成两段,再将每段分别围成正方形(如图),如果这两个正方形的面积和等于160cm2,求两个正方形的边长。
几何图形问题
分析:
(1)题目中的已知量、未
知量各是什么?
(2)量与量的关系是什么?
(3)等量关系是什么?
(4) 怎样设未知数?
关系式:①两正方形的周长之和=64
②两正方形的面积之和=160
解:设其中一个正方形的边长为
xcm,那么另一个正方形的边
长为 ,
根据题意,得
x2 +(16-x)2=160
整理,得 x2 -16x+48=0
解,得 x1 =12,x2=4
经检验,当两个正方形的边长分别是12cm和4cm时,都符合题意.
∴两个正方形的边长分别是12cm和4cm.
例2、有一块长40m,宽30m的矩形铁片,在它的四周截去一个全等的小正方形,然后折成一个无盖的长方体盒子,怎样截能使底面积所占面积为原来矩形面积的一半?
40m
30m
xm
xm
例题讲解
几何图形问题
分析:
(1)题目中的已知量、未知量各是什么?怎样设未知数?
(2)无盖长方体盒子的底面的长和宽怎么表示?
(3)等量关系是什么?
40m
30m
xm
xm
解:设剪去的正方形的边长为
xcm,根据题意,得
整理,得 x2 -35x+150=0
解,得 x1 =5,x2=30
经检验,当x2=30=30,不合题意,舍去.
∴截去的正方形的边长为5cm.
例3、MN是一面长10m的墙,用长24m的篱笆,围成一个一面是墙,中间隔着一道篱笆的矩形花圃ABCD,已知花圃的设计面积为45m2,花圃的宽AB应当是多少?
10m
A
B
C
D
M
N
例题讲解
几何图形问题
分析:
(1)题目中的已知量、未知量各是什么?
怎样设未知数?
(2)矩形花圃ABCD的长和宽怎么表示?
(3)等量关系是什么?
(4)矩形花圃ABCD的长BC的取值范围是什么?
解:设花圃的宽AB为xcm,则长BC为(24-3x)cm,根据题意,得
整理,得 x2 -8x+15=0
解,得 x1 =3,x2=5
经检验,当x1=3时,
24-3x=15>10
不合题意,舍去.
∴花圃的宽AB为5cm.
10m
A
B
C
D
M
N
例题讲解
销售问题
例4、某花圃用花盆培育某种花卉,经市场调查发现,出售一盆花的盈利与该盆中花的棵树有关,当每盆栽种3课时,平均每棵盈利3元。以同样的栽培条件,每盆增加1棵,平均每棵的盈利将减少0.5元.要使每盆的盈利达到10元,每盆应当种植花卉多少棵?
分析:
(1)怎样设未知数?每盆栽种的花的棵数怎么表示?
(2)每盆中每棵花的盈利怎么表示?
(3)每盆花的总盈利怎么表示?
(4)等量关系是什么?
解:设每盆中增加种植x棵,则每盆种花(3+x)棵,平均每棵花的盈利为(3-0.5x)元,根据题意,得
整理,得 x2 -3x+2=0
解,得 x1 =1,x2=2
经检验,x1=1,x2=2
均合题意.
∴每盆应种植该种花4棵或5棵.
∴ 3+x =4或5
例题讲解
销售问题
例5、将进货单价40元的商品按50元出售时,售出500个。经市场调查发现,该商品每涨价1元,其销量减少10个,为了赚8000元的利润,则售价应定为多少元?
分析: 为了赚8000元的利润时
(1)怎样设未知数?该商品每个的售价怎么表示?
(2)该商品每个的盈利怎么表示?
(3)该商品的销售数量怎么表示?
(4)该商品的总盈利 怎么表示?
(5)等量关系是什么?
解:设该商品每个涨价x元,则根据题意,得
整理,得 x2 -40x+300=0
解,得 x1 =30,x2=10
经检验,x1=30,x2=10
均合题意.
∴该商品的售价为80元或60元.
∴售价为 50+x =80或60
例题讲解
销售问题
例6、某专卖店销售某种脐橙,其进价是每千克40元,按每千克60元出售时,平均每天可售出100千克。经市场调查发现,该脐橙每千克降价2元,其平均每天的销量可增加20千克,若该专卖店要想平均每天获利2240元,为尽快减少库存,则每千克脐橙应降价多少元?
分析: 为了赚2240元的利润时
(1)怎样设未知数?该脐橙每千克的售价怎么表示?
(2)该脐橙每千克的盈利怎么表示?
(3)该脐橙每天的销售数量怎么表示?
(4)该脐橙每天的总盈利 怎么表示?
(5)等量关系是什么?
解:设该脐橙每千克降价x元,则根据题意,得
整理,得 x2 -10x+24=0
解,得 x1 =4,x2=6
经检验,∵为了减少库存
∴x1=4不合题意,舍去.
∴每千克脐橙应降价6元.
练 习
P152 练习 第1、2题
1、列方程(组)解应用题的方法步骤:
(1)审题:
(2)设未知数:
(3)列方程(组):
(4)解方程(组):
(5)检验:
(6)写答:
(找题目中的已知量、未知量、量与量的关
系及等量关系)
(间接设或直接设)
(根据量与量的关系及等量关系)
(验根是否是所列方程的解,且是否符合题意)
知识总结
2、列一元二次方程解应用题必须进行检验。
作 业
P154 习题4.7 第1、2、3、4、8题
结束寄语
数学的目的在于应用。 宇宙、大自然、天地万物之间都存在着奇妙的数学关系,认识它们是多么美妙的事啊!
再 见
4.7 一元二次方程的应用
青岛版 数学 九(上) 第四章: 一元二次方程
复习回顾
1、列方程(组)解应用题的方法步骤:
(1)审题:
(2)设未知数:
(3)列方程(组):
(4)解方程(组):
(5)检验:
(6)写答:
(找题目中的已知量、未知量、量与量的关
系及等量关系)
(间接设或直接设)
(根据量与量的关系及等量关系)
(验根是否是所列方程的解,且是否符合题意)
2、列方程(组)解应用题时的题型:
注意:各类型的题目还有各类型的独立关系式.
复习回顾
(1)行程问题:
(2)工程问题:
(4)图形的面积(或体积)问题:
(3)市场营销问题:
(5)银行存款问题:
(6)利率问题:
(7)数字问题;等等
同样,与我们学习过的一元一次方程、二元一次方程组和分式方程一样,一元二次方程也是刻画现实生活和生产中数量关系的有效模型.
例题讲解
例1、将一根长64cm的铁丝剪成两段,再将每段分别围成正方形(如图),如果这两个正方形的面积和等于160cm2,求两个正方形的边长。
几何图形问题
分析:
(1)题目中的已知量、未
知量各是什么?
(2)量与量的关系是什么?
(3)等量关系是什么?
(4) 怎样设未知数?
关系式:①两正方形的周长之和=64
②两正方形的面积之和=160
解:设其中一个正方形的边长为
xcm,那么另一个正方形的边
长为 ,
根据题意,得
x2 +(16-x)2=160
整理,得 x2 -16x+48=0
解,得 x1 =12,x2=4
经检验,当两个正方形的边长分别是12cm和4cm时,都符合题意.
∴两个正方形的边长分别是12cm和4cm.
例2、有一块长40m,宽30m的矩形铁片,在它的四周截去一个全等的小正方形,然后折成一个无盖的长方体盒子,怎样截能使底面积所占面积为原来矩形面积的一半?
40m
30m
xm
xm
例题讲解
几何图形问题
分析:
(1)题目中的已知量、未知量各是什么?怎样设未知数?
(2)无盖长方体盒子的底面的长和宽怎么表示?
(3)等量关系是什么?
40m
30m
xm
xm
解:设剪去的正方形的边长为
xcm,根据题意,得
整理,得 x2 -35x+150=0
解,得 x1 =5,x2=30
经检验,当x2=30=30,不合题意,舍去.
∴截去的正方形的边长为5cm.
例3、MN是一面长10m的墙,用长24m的篱笆,围成一个一面是墙,中间隔着一道篱笆的矩形花圃ABCD,已知花圃的设计面积为45m2,花圃的宽AB应当是多少?
10m
A
B
C
D
M
N
例题讲解
几何图形问题
分析:
(1)题目中的已知量、未知量各是什么?
怎样设未知数?
(2)矩形花圃ABCD的长和宽怎么表示?
(3)等量关系是什么?
(4)矩形花圃ABCD的长BC的取值范围是什么?
解:设花圃的宽AB为xcm,则长BC为(24-3x)cm,根据题意,得
整理,得 x2 -8x+15=0
解,得 x1 =3,x2=5
经检验,当x1=3时,
24-3x=15>10
不合题意,舍去.
∴花圃的宽AB为5cm.
10m
A
B
C
D
M
N
例题讲解
销售问题
例4、某花圃用花盆培育某种花卉,经市场调查发现,出售一盆花的盈利与该盆中花的棵树有关,当每盆栽种3课时,平均每棵盈利3元。以同样的栽培条件,每盆增加1棵,平均每棵的盈利将减少0.5元.要使每盆的盈利达到10元,每盆应当种植花卉多少棵?
分析:
(1)怎样设未知数?每盆栽种的花的棵数怎么表示?
(2)每盆中每棵花的盈利怎么表示?
(3)每盆花的总盈利怎么表示?
(4)等量关系是什么?
解:设每盆中增加种植x棵,则每盆种花(3+x)棵,平均每棵花的盈利为(3-0.5x)元,根据题意,得
整理,得 x2 -3x+2=0
解,得 x1 =1,x2=2
经检验,x1=1,x2=2
均合题意.
∴每盆应种植该种花4棵或5棵.
∴ 3+x =4或5
例题讲解
销售问题
例5、将进货单价40元的商品按50元出售时,售出500个。经市场调查发现,该商品每涨价1元,其销量减少10个,为了赚8000元的利润,则售价应定为多少元?
分析: 为了赚8000元的利润时
(1)怎样设未知数?该商品每个的售价怎么表示?
(2)该商品每个的盈利怎么表示?
(3)该商品的销售数量怎么表示?
(4)该商品的总盈利 怎么表示?
(5)等量关系是什么?
解:设该商品每个涨价x元,则根据题意,得
整理,得 x2 -40x+300=0
解,得 x1 =30,x2=10
经检验,x1=30,x2=10
均合题意.
∴该商品的售价为80元或60元.
∴售价为 50+x =80或60
例题讲解
销售问题
例6、某专卖店销售某种脐橙,其进价是每千克40元,按每千克60元出售时,平均每天可售出100千克。经市场调查发现,该脐橙每千克降价2元,其平均每天的销量可增加20千克,若该专卖店要想平均每天获利2240元,为尽快减少库存,则每千克脐橙应降价多少元?
分析: 为了赚2240元的利润时
(1)怎样设未知数?该脐橙每千克的售价怎么表示?
(2)该脐橙每千克的盈利怎么表示?
(3)该脐橙每天的销售数量怎么表示?
(4)该脐橙每天的总盈利 怎么表示?
(5)等量关系是什么?
解:设该脐橙每千克降价x元,则根据题意,得
整理,得 x2 -10x+24=0
解,得 x1 =4,x2=6
经检验,∵为了减少库存
∴x1=4不合题意,舍去.
∴每千克脐橙应降价6元.
练 习
P152 练习 第1、2题
1、列方程(组)解应用题的方法步骤:
(1)审题:
(2)设未知数:
(3)列方程(组):
(4)解方程(组):
(5)检验:
(6)写答:
(找题目中的已知量、未知量、量与量的关
系及等量关系)
(间接设或直接设)
(根据量与量的关系及等量关系)
(验根是否是所列方程的解,且是否符合题意)
知识总结
2、列一元二次方程解应用题必须进行检验。
作 业
P154 习题4.7 第1、2、3、4、8题
结束寄语
数学的目的在于应用。 宇宙、大自然、天地万物之间都存在着奇妙的数学关系,认识它们是多么美妙的事啊!
再 见
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
