2022-2023学年苏科版数学九年级上册 2.2圆的对称性 同步达标测试题 (Word版含答案)
文档属性
| 名称 | 2022-2023学年苏科版数学九年级上册 2.2圆的对称性 同步达标测试题 (Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 550.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-05 17:58:41 | ||
图片预览



文档简介
2022-2023学年苏科版九年级数学上册《2.2圆的对称性》同步达标测试题(附答案)
一.选择题(共8小题,满分40分)
1.如图AB是⊙O的直径,弦CD⊥AB,垂足为E,若BE=CD=8,则⊙O半径长是( )
A.5 B.4 C.3 D.2
2.如图,正方形ABCD和正方形BEFG的顶点分别在半圆O的直径和圆周上,若BG=4,则半圆O的半径是( )
A.4+ B.9 C.4 D.6
3.在圆中,与半径相等的弦所对的圆心角的度数为( )
A.30° B.45° C.60° D.90°
4.如图,扇形OAB中,∠AOB=120°,半径OA=6,C是弧AB的中点,CD⊥OA,交AB于点D,则CD的长为( )
A. B.3 C. D.2
5.⊙O的直径AB和弦CD相交于点E,已知AE=6,EB=2,∠CEA=30°,则弦CD的长为( )
A.8 B.4 C.2 D.2
6.如图,⊙O中,弦AB⊥AC,OE⊥AB,垂足为E,OF⊥AC,垂足为F,若AB+AC=10,则四边形OEAF的周长为( )
A.10. B.9 C.8 D.7
7.已知⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8cm,则AC的长为( )
A.2cm B.4cm
C.2cm或4cm D.2cm或4cm
8.如图,AB是⊙O的直径,CD为⊙O的弦,且CD⊥AB于点E,点F为圆上一点,若AE=BF,,OE=1,则BC的长为( )
A.2 B.3 C.4 D.5
二.填空题(共8小题,满分40分)
9.在⊙O中,圆心角∠AOB=90°,点O到弦AB的距离为4,则⊙O的半径的长为 .
10.如图,AD是⊙O的直径,AD⊥BC于E,若DE=3,BC=8,则⊙O的半径为 .
11.在半径为13cm的圆内有两条互相平行的弦,一条弦长为24cm,另一条弦长为10cm,则这两条弦之间的距离为 cm.
如图,在△ABC中,∠B=70°,⊙O截三边所得的弦长DE=FG=HI,
则∠AOC= 度.
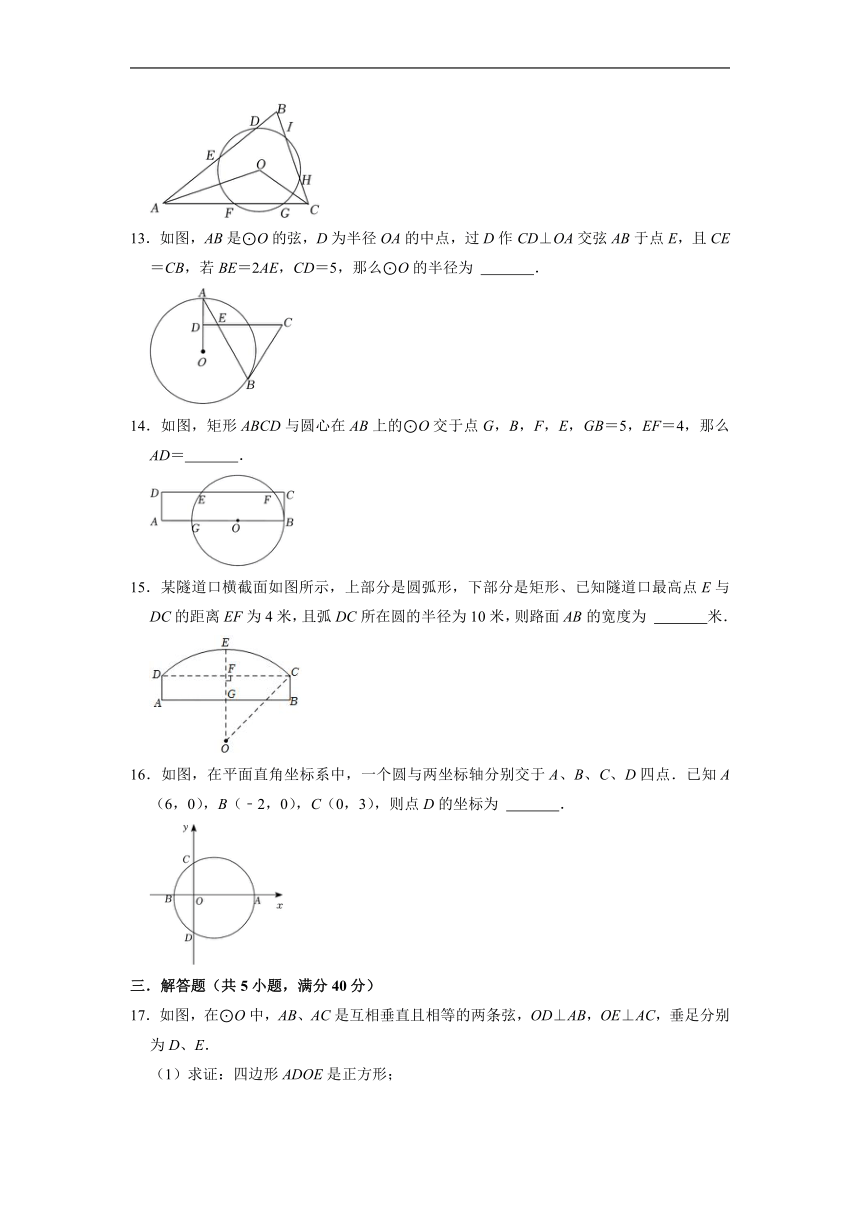
13.如图,AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦AB于点E,且CE=CB,若BE=2AE,CD=5,那么⊙O的半径为 .
14.如图,矩形ABCD与圆心在AB上的⊙O交于点G,B,F,E,GB=5,EF=4,那么AD= .
15.某隧道口横截面如图所示,上部分是圆弧形,下部分是矩形、已知隧道口最高点E与DC的距离EF为4米,且弧DC所在圆的半径为10米,则路面AB的宽度为 米.
16.如图,在平面直角坐标系中,一个圆与两坐标轴分别交于A、B、C、D四点.已知A(6,0),B(﹣2,0),C(0,3),则点D的坐标为 .
三.解答题(共5小题,满分40分)
17.如图,在⊙O中,AB、AC是互相垂直且相等的两条弦,OD⊥AB,OE⊥AC,垂足分别为D、E.
(1)求证:四边形ADOE是正方形;
(2)若AC=2cm,求⊙O的半径.
18.如图,⊙O的半径长为5,AB为⊙O的直径,弦AC的长为8,点D为的中点.求弦DC的长.
19.石拱桥是我国古代入民勤劳和智慧的结晶(如图1),隋代建造的赵州桥距今约有1400年历史,是我国古代石拱桥的代表.如图2是根据某石拱桥的实物图画出的几何图形,桥的主桥拱是圆弧形,表示为.桥的跨度(弧所对的弦长)AB=26m,设所在圆的圆心为O,半径OC⊥AB,垂足为D.拱高(弧的中点到弦的距离)CD=5m.连接OB.
(1)直接判断AD与BD的数量关系;
(2)求这座石拱桥主桥拱的半径(精确到1m).
20.如图,在⊙O中,AB,AC为弦,CD为直径,AB⊥CD于E,BF⊥AC于F,BF与CD相交于G.
(1)求证:ED=EG;
(2)若AB=8,OG=1,求⊙O的半径.
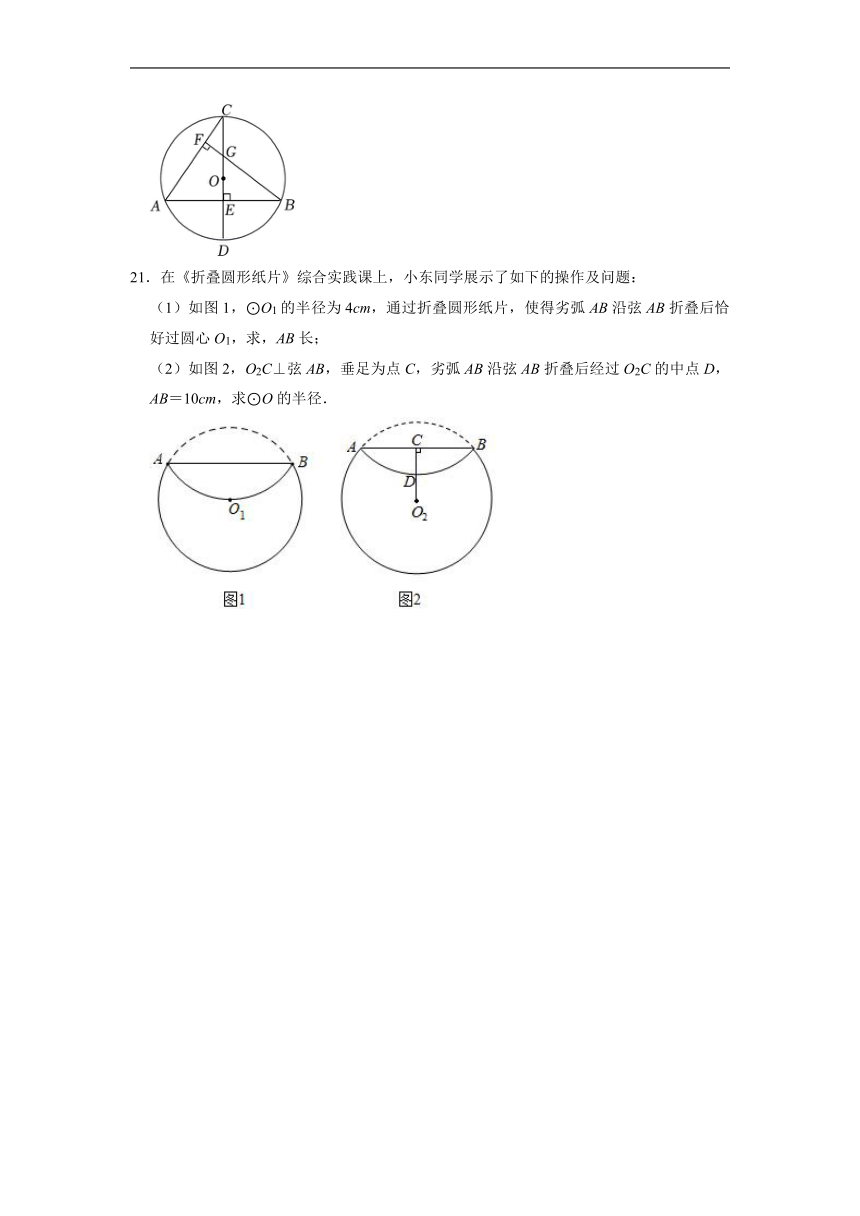
21.在《折叠圆形纸片》综合实践课上,小东同学展示了如下的操作及问题:
(1)如图1,⊙O1的半径为4cm,通过折叠圆形纸片,使得劣弧AB沿弦AB折叠后恰好过圆心O1,求,AB长;
(2)如图2,O2C⊥弦AB,垂足为点C,劣弧AB沿弦AB折叠后经过O2C的中点D,AB=10cm,求⊙O的半径.
参考答案
一.选择题(共8小题,满分40分)
1.解:连接OC,
设⊙O的半径为R,则OE=8﹣R,
∵CD⊥AB,AB过圆心O,CD=8,
∴∠OEC=90°,CE=DE=4,
由勾股定理得:OC2=CE2+OE2,
R2=42+(8﹣R)2,
解得:R=5,
即⊙O的半径长是5,
故选:A.
2.解:连接OC,OF,
设OB=x,
∵四边形ABCD是正方形且顶点D和C在圆上,
∴AB=BC=2x,∠OBC=90°,
∵BG=4,四边形BEFG是正方形,
∴OE=x+4,EF=BE=BG=4,∠FEB=90°,
在Rt△BCO中,OC=,
在Rt△FEO中,OF=,
∵OF=OC,
∴5x2=x2+8x+32,
解得x=4或x=﹣2(舍去)
当x=4时,OC=4,
则半圆O的半径是4.
故选:C.
3.解:如图,
∵OA=OB=AB,
∴△OAB是等边三角形,
∴∠AOB=60°.
故选:C.
4.解:连接OC,交AB于F,
∵C是的中点,
∴,
∴∠AOC=∠BOC=∠AOB==60°,OC⊥AB,
Rt△BOF中,OB=OA=6,
∴OF=OB=3,
∴CF=6﹣3=3,
∵CD⊥OA,
∴∠OEC=90°,
∴∠OCE=30°,
∵∠CFD=90°,
∴DF=,CD=2DF=2,
故选:D.
5.解:过点O作OM⊥CD,连接OC,
则CD=2CM,
∵AE=6,EB=2,
∴AB=8,
∴OC=OB=4,
∴OE=4﹣2=2,
∵∠CEA=30°,
∴OM=OE=×2=1,
∴CM===,
∴CD=2.
故选:C.
6.解:∵AB⊥AC,OE⊥AB,OF⊥AC,
∴四边形OEAF是矩形,
∴四边形OEAF的周长=2(AF+AE)=2×(AB+AC)=10.
故选:A.
7.解:连接AC,AO,
∵⊙O的直径CD=10cm,AB⊥CD,AB=8cm,
∴AM=AB=×8=4(cm),OD=OC=5cm,
当C点位置如图1所示时,
∵OA=5cm,AM=4cm,CD⊥AB,
∴OM===3(cm),
∴CM=OC+OM=5+3=8(cm),
∴AC===4(cm);
当C点位置如图2所示时,同理可得OM=3cm,
∵OC=5cm,
∴MC=5﹣3=2(cm),
在Rt△AMC中,AC===2(cm).
故选:C.
8.解:如图,连接OC交AF于J,设BC交AF于T,过点T作TH⊥AB于H.
∵AB⊥CD,
∴=,
∵=,
∴=,
∴OC⊥AF,
∴∠AJO=∠CEO=90°,
∵∠AOJ=∠COE,OA=OC,
∴△AJO≌△CEO(AAS),
∴OJ=OE,
∴AE=CJ,
∵AB是直径,
∴∠F=∠CJT=90°,
∵AE=BF,
∴BF=CJ,
∵∠CTJ=∠BTF,
∴△CTJ≌△BTF(AAS),
∴CT=BT,
∵TH⊥AB,CD⊥AB,
∴TH∥CE,
∴EH=BH,
∵=,
∴∠TBF=∠TBH,
∵∠F=∠THB=90°,BT=BT,
∴△BTF≌△BTH(AAS),
∴BF=BH,
∵AE=BF,
∴AE=BH,
∵OA=OB,
∴OE=OH=1,
∴EH=BH=2,
∴AE=BH=2,
∴AB=6,OC=OB=3,
∴EC===2,
∴BC===2,
故选:A.
二.填空题(共8小题,满分40分)
9.解:如图,过点O作OC⊥AB,垂足为C,
∵∠AOB=90°,∠A=∠AOC=45°,
∴OC=AC,
∵CO=4,
∴AC=4,
∴OA=4,
∴⊙O的半径长为4.
故答案为:4.
10.解:连接OC,如图,设⊙O的半径为r,
∵AD⊥BC,
∴CE=BE=BC=4,
在Rt△OCE中,(r﹣3)2+42=r2,
解得r=.
即⊙O的半径为.
故答案为:
11.解:有两种情况:①如图,当AB和CD在O的两旁时,
过O作MN⊥AB于M,交CD于N,连接OB,OD,
∵AB∥CD,
∴MN⊥CD,
由垂径定理得:BM=AB=12,DN=CD=5,
∵OB=OD=10,
由勾股定理得:OM==5,
同理ON=12,
∴MN=5+12=17,
②当AB和CD在O的同旁时,MN=12﹣5=7.
故答案为:17或7.
12.解:过点O作OM⊥DE于M,OK⊥FG于K,OP⊥HI于P,如图,
∵DE=FG=HI,
∴OM=OK=OP,
∴OA平分∠BAC,OC平分∠ACB,
∴∠OAC=BAC,∠OCA=BCA,
∵∠B=70°,
∴∠BAC+∠BCA=180°﹣∠B=110°,
∴∠OAC+∠OCA
=(∠BAC+∠ACB)
=×110°
=55°,
∴∠AOC=180°﹣(∠OAC+∠OCA)
=180°﹣55°
=125°,
故答案为:125.
13.解:如图,记DC与⊙O交于点F,连接AF、OF、OB,过点C作CT⊥AB于点T,连接OE,OT.
∵D为半径OA的中点,CD⊥OA,
∴FD垂直平分AO,
∴FA=FO,
又∵OA=OF,
∴△AOF是等边三角形,
∴∠OAF=∠AOF=∠AFO=60°,
∵CE=CB,CT⊥EB,
∴ET=TB,
∵BE=2AE,
∴AE=ET=BT,
∵AD=OD,
∴DE∥OT,
∴∠AOT=∠ADE=90°,
∴OE=AE=ET,
∵OA=OB,
∴∠OAE=∠OBT,
∵AO=BO,AE=BT,
∴△AOE≌△BOT(SAS),
∴OE=OT,
∴OE=OT=ET,
∴∠ETO=60°,
∴∠OAB=∠OBA=30°,∠AED=∠CEB=60°,
∴△CEB是等边三角形,
∴CE=CB=BE,
设DE=x,
∴AE=2x,BE=CE=4x,
∴CD=5x=5,
∴x=1,
∴AD=,
∴AO=2.
故答案为:2.
14.解:过O作OM⊥EF于M,连接OE,则∠OMD=90°,
∵四边形ABCD是矩形,
∴∠A=∠D=90°,
∴四边形AOMD是矩形,
∴OM=AD,
∵OM⊥EF,OM过圆心O,EF=4,
∴EM=FM=2,
∵OG=OB,BG=5,
∴OB=OG=2.5=OE,
在Rt△OME中,由勾股定理得:OM===1.5,
∴AD=OM=1.5,
故答案为:1.5.
15.解:设圆弧形所在圆的圆心为O,由题意可知,点O在EF的延长线上,连接OC,
∵OE⊥CD,
∴∠CFO=90°,CF=DF,
在Rt△CFO中,OC=10,OF=OE﹣EF=10﹣4=6,
∴CF===8,
∴AB=CD=2CF=16,
即路面AB的宽度为16米.
故答案为:16.
16.解:设圆心为P,过点P作PE⊥AB于点E,PF⊥CD于点F,则EA=EB==4,FC=FD,
∴OE=EB﹣OB=4﹣2=2,
∴E(2,0),
设P(2,m),则F(0,m),
连接PC、PA,
在Rt△CPF中,PC2=(3﹣m)2+22,
在Rt△APE中,PA2=m2+42,
∵PA=PC,
∴(3﹣m)2+22=m2+42,
∴m=(舍正),
∴F(0,),
∴CF=DF==,
∴OD=OF+DF==4,
∴D(0,﹣4),
故答案为:(0,﹣4).
三.解答题(共5小题,满分40分)
17.(1)证明:∵OD⊥AB,OE⊥AC,
∴AD=AB,AE=AC,
∵AB=AC,
∴AD=AE,
∵∠ADO=∠A=∠AEO=90°,
∴四边形ADOE是正方形;
(2)解:连接OA,
∵AC=2cm,
∴AE=1cm,
在Rt△AOE中,OA==(cm),
答:⊙O的半径是cm.
18.解:连接DO并延长交AC于点E,
∵点D为弧ABC的中点,
∵DE⊥AC,且AE=EC,
AC=8,.AE=EC=4
∵DO=AO=5,
∴OE=3,
∴DE=8,
∴在Rt△DEC中,
DC==.
19.解:(1)∵OC⊥AB,
∴AD=BD;
(2)设主桥拱半径为R,由题意可知AB=26,CD=5,
∴BD=AB=13,
OD=OC﹣CD=R﹣5,
∵∠OBD=90°,
∴OD2+BD2=OB2,
∴(R﹣5)2+132=R2,
解得R=19.4≈19,
答:这座石拱桥主桥拱的半径约为19m.
20.(1)证明:如图:连接BD,
∵AB⊥CD于E,BF⊥AC于F,
∴∠CFG=∠GEB,
∵∠CGF=∠BGE,
∴∠C=∠GBE,
∵∠C=∠DBE,
∴∠GBE=∠DBE,
∵AB⊥CD于E,
∴∠GEB=∠DEB,
在△GBE和△DBE中,
,
∴△BGE≌△BDE(ASA),
∴ED=EG.
(2)解:如图:
连接OA,设OA=r,则DG=r+1,
由(1)可知ED=EG,
∴OE=,
∵AB⊥CD于E,AB=8,
∴AE=BE=4,
∴在Rt△OAE中,根据勾股定理得:OE2+AE2=OA2,
即()2+42=r2,
解得:r=,
即⊙O的半径为.
21.解:(1)如图1,过点O1作O1F⊥AB于F,并延长O1F交虚线劣弧AB于E,
∴AB=2AF,
由折叠知,EF=O1F=O1E=×4=2(cm),
连接O1A,
在Rt△O1FA中,O1A=4,
根据勾股定理得,AF===2(cm),
∴AB=2AF=4cm;
(2)如图2,延长O2C交虚线劣弧AB于G,
由折叠知,CG=CD,
∵D是O2C的中点,
∴CD=O2D,
∴CG=CD=O2D,
设⊙O2的半径为3rcm,则O2C=2r(cm),
∵O2C⊥弦AB,
∴AC=AB=5(cm),
连接O2A,
在Rt△ACO2中,根据勾股定理得,(3r)2﹣(2r)2=25,
∴r=(舍去负值),
∴O2A=3r=3(cm),
即⊙O2的半径为3cm.
一.选择题(共8小题,满分40分)
1.如图AB是⊙O的直径,弦CD⊥AB,垂足为E,若BE=CD=8,则⊙O半径长是( )
A.5 B.4 C.3 D.2
2.如图,正方形ABCD和正方形BEFG的顶点分别在半圆O的直径和圆周上,若BG=4,则半圆O的半径是( )
A.4+ B.9 C.4 D.6
3.在圆中,与半径相等的弦所对的圆心角的度数为( )
A.30° B.45° C.60° D.90°
4.如图,扇形OAB中,∠AOB=120°,半径OA=6,C是弧AB的中点,CD⊥OA,交AB于点D,则CD的长为( )
A. B.3 C. D.2
5.⊙O的直径AB和弦CD相交于点E,已知AE=6,EB=2,∠CEA=30°,则弦CD的长为( )
A.8 B.4 C.2 D.2
6.如图,⊙O中,弦AB⊥AC,OE⊥AB,垂足为E,OF⊥AC,垂足为F,若AB+AC=10,则四边形OEAF的周长为( )
A.10. B.9 C.8 D.7
7.已知⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8cm,则AC的长为( )
A.2cm B.4cm
C.2cm或4cm D.2cm或4cm
8.如图,AB是⊙O的直径,CD为⊙O的弦,且CD⊥AB于点E,点F为圆上一点,若AE=BF,,OE=1,则BC的长为( )
A.2 B.3 C.4 D.5
二.填空题(共8小题,满分40分)
9.在⊙O中,圆心角∠AOB=90°,点O到弦AB的距离为4,则⊙O的半径的长为 .
10.如图,AD是⊙O的直径,AD⊥BC于E,若DE=3,BC=8,则⊙O的半径为 .
11.在半径为13cm的圆内有两条互相平行的弦,一条弦长为24cm,另一条弦长为10cm,则这两条弦之间的距离为 cm.
如图,在△ABC中,∠B=70°,⊙O截三边所得的弦长DE=FG=HI,
则∠AOC= 度.
13.如图,AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦AB于点E,且CE=CB,若BE=2AE,CD=5,那么⊙O的半径为 .
14.如图,矩形ABCD与圆心在AB上的⊙O交于点G,B,F,E,GB=5,EF=4,那么AD= .
15.某隧道口横截面如图所示,上部分是圆弧形,下部分是矩形、已知隧道口最高点E与DC的距离EF为4米,且弧DC所在圆的半径为10米,则路面AB的宽度为 米.
16.如图,在平面直角坐标系中,一个圆与两坐标轴分别交于A、B、C、D四点.已知A(6,0),B(﹣2,0),C(0,3),则点D的坐标为 .
三.解答题(共5小题,满分40分)
17.如图,在⊙O中,AB、AC是互相垂直且相等的两条弦,OD⊥AB,OE⊥AC,垂足分别为D、E.
(1)求证:四边形ADOE是正方形;
(2)若AC=2cm,求⊙O的半径.
18.如图,⊙O的半径长为5,AB为⊙O的直径,弦AC的长为8,点D为的中点.求弦DC的长.
19.石拱桥是我国古代入民勤劳和智慧的结晶(如图1),隋代建造的赵州桥距今约有1400年历史,是我国古代石拱桥的代表.如图2是根据某石拱桥的实物图画出的几何图形,桥的主桥拱是圆弧形,表示为.桥的跨度(弧所对的弦长)AB=26m,设所在圆的圆心为O,半径OC⊥AB,垂足为D.拱高(弧的中点到弦的距离)CD=5m.连接OB.
(1)直接判断AD与BD的数量关系;
(2)求这座石拱桥主桥拱的半径(精确到1m).
20.如图,在⊙O中,AB,AC为弦,CD为直径,AB⊥CD于E,BF⊥AC于F,BF与CD相交于G.
(1)求证:ED=EG;
(2)若AB=8,OG=1,求⊙O的半径.
21.在《折叠圆形纸片》综合实践课上,小东同学展示了如下的操作及问题:
(1)如图1,⊙O1的半径为4cm,通过折叠圆形纸片,使得劣弧AB沿弦AB折叠后恰好过圆心O1,求,AB长;
(2)如图2,O2C⊥弦AB,垂足为点C,劣弧AB沿弦AB折叠后经过O2C的中点D,AB=10cm,求⊙O的半径.
参考答案
一.选择题(共8小题,满分40分)
1.解:连接OC,
设⊙O的半径为R,则OE=8﹣R,
∵CD⊥AB,AB过圆心O,CD=8,
∴∠OEC=90°,CE=DE=4,
由勾股定理得:OC2=CE2+OE2,
R2=42+(8﹣R)2,
解得:R=5,
即⊙O的半径长是5,
故选:A.
2.解:连接OC,OF,
设OB=x,
∵四边形ABCD是正方形且顶点D和C在圆上,
∴AB=BC=2x,∠OBC=90°,
∵BG=4,四边形BEFG是正方形,
∴OE=x+4,EF=BE=BG=4,∠FEB=90°,
在Rt△BCO中,OC=,
在Rt△FEO中,OF=,
∵OF=OC,
∴5x2=x2+8x+32,
解得x=4或x=﹣2(舍去)
当x=4时,OC=4,
则半圆O的半径是4.
故选:C.
3.解:如图,
∵OA=OB=AB,
∴△OAB是等边三角形,
∴∠AOB=60°.
故选:C.
4.解:连接OC,交AB于F,
∵C是的中点,
∴,
∴∠AOC=∠BOC=∠AOB==60°,OC⊥AB,
Rt△BOF中,OB=OA=6,
∴OF=OB=3,
∴CF=6﹣3=3,
∵CD⊥OA,
∴∠OEC=90°,
∴∠OCE=30°,
∵∠CFD=90°,
∴DF=,CD=2DF=2,
故选:D.
5.解:过点O作OM⊥CD,连接OC,
则CD=2CM,
∵AE=6,EB=2,
∴AB=8,
∴OC=OB=4,
∴OE=4﹣2=2,
∵∠CEA=30°,
∴OM=OE=×2=1,
∴CM===,
∴CD=2.
故选:C.
6.解:∵AB⊥AC,OE⊥AB,OF⊥AC,
∴四边形OEAF是矩形,
∴四边形OEAF的周长=2(AF+AE)=2×(AB+AC)=10.
故选:A.
7.解:连接AC,AO,
∵⊙O的直径CD=10cm,AB⊥CD,AB=8cm,
∴AM=AB=×8=4(cm),OD=OC=5cm,
当C点位置如图1所示时,
∵OA=5cm,AM=4cm,CD⊥AB,
∴OM===3(cm),
∴CM=OC+OM=5+3=8(cm),
∴AC===4(cm);
当C点位置如图2所示时,同理可得OM=3cm,
∵OC=5cm,
∴MC=5﹣3=2(cm),
在Rt△AMC中,AC===2(cm).
故选:C.
8.解:如图,连接OC交AF于J,设BC交AF于T,过点T作TH⊥AB于H.
∵AB⊥CD,
∴=,
∵=,
∴=,
∴OC⊥AF,
∴∠AJO=∠CEO=90°,
∵∠AOJ=∠COE,OA=OC,
∴△AJO≌△CEO(AAS),
∴OJ=OE,
∴AE=CJ,
∵AB是直径,
∴∠F=∠CJT=90°,
∵AE=BF,
∴BF=CJ,
∵∠CTJ=∠BTF,
∴△CTJ≌△BTF(AAS),
∴CT=BT,
∵TH⊥AB,CD⊥AB,
∴TH∥CE,
∴EH=BH,
∵=,
∴∠TBF=∠TBH,
∵∠F=∠THB=90°,BT=BT,
∴△BTF≌△BTH(AAS),
∴BF=BH,
∵AE=BF,
∴AE=BH,
∵OA=OB,
∴OE=OH=1,
∴EH=BH=2,
∴AE=BH=2,
∴AB=6,OC=OB=3,
∴EC===2,
∴BC===2,
故选:A.
二.填空题(共8小题,满分40分)
9.解:如图,过点O作OC⊥AB,垂足为C,
∵∠AOB=90°,∠A=∠AOC=45°,
∴OC=AC,
∵CO=4,
∴AC=4,
∴OA=4,
∴⊙O的半径长为4.
故答案为:4.
10.解:连接OC,如图,设⊙O的半径为r,
∵AD⊥BC,
∴CE=BE=BC=4,
在Rt△OCE中,(r﹣3)2+42=r2,
解得r=.
即⊙O的半径为.
故答案为:
11.解:有两种情况:①如图,当AB和CD在O的两旁时,
过O作MN⊥AB于M,交CD于N,连接OB,OD,
∵AB∥CD,
∴MN⊥CD,
由垂径定理得:BM=AB=12,DN=CD=5,
∵OB=OD=10,
由勾股定理得:OM==5,
同理ON=12,
∴MN=5+12=17,
②当AB和CD在O的同旁时,MN=12﹣5=7.
故答案为:17或7.
12.解:过点O作OM⊥DE于M,OK⊥FG于K,OP⊥HI于P,如图,
∵DE=FG=HI,
∴OM=OK=OP,
∴OA平分∠BAC,OC平分∠ACB,
∴∠OAC=BAC,∠OCA=BCA,
∵∠B=70°,
∴∠BAC+∠BCA=180°﹣∠B=110°,
∴∠OAC+∠OCA
=(∠BAC+∠ACB)
=×110°
=55°,
∴∠AOC=180°﹣(∠OAC+∠OCA)
=180°﹣55°
=125°,
故答案为:125.
13.解:如图,记DC与⊙O交于点F,连接AF、OF、OB,过点C作CT⊥AB于点T,连接OE,OT.
∵D为半径OA的中点,CD⊥OA,
∴FD垂直平分AO,
∴FA=FO,
又∵OA=OF,
∴△AOF是等边三角形,
∴∠OAF=∠AOF=∠AFO=60°,
∵CE=CB,CT⊥EB,
∴ET=TB,
∵BE=2AE,
∴AE=ET=BT,
∵AD=OD,
∴DE∥OT,
∴∠AOT=∠ADE=90°,
∴OE=AE=ET,
∵OA=OB,
∴∠OAE=∠OBT,
∵AO=BO,AE=BT,
∴△AOE≌△BOT(SAS),
∴OE=OT,
∴OE=OT=ET,
∴∠ETO=60°,
∴∠OAB=∠OBA=30°,∠AED=∠CEB=60°,
∴△CEB是等边三角形,
∴CE=CB=BE,
设DE=x,
∴AE=2x,BE=CE=4x,
∴CD=5x=5,
∴x=1,
∴AD=,
∴AO=2.
故答案为:2.
14.解:过O作OM⊥EF于M,连接OE,则∠OMD=90°,
∵四边形ABCD是矩形,
∴∠A=∠D=90°,
∴四边形AOMD是矩形,
∴OM=AD,
∵OM⊥EF,OM过圆心O,EF=4,
∴EM=FM=2,
∵OG=OB,BG=5,
∴OB=OG=2.5=OE,
在Rt△OME中,由勾股定理得:OM===1.5,
∴AD=OM=1.5,
故答案为:1.5.
15.解:设圆弧形所在圆的圆心为O,由题意可知,点O在EF的延长线上,连接OC,
∵OE⊥CD,
∴∠CFO=90°,CF=DF,
在Rt△CFO中,OC=10,OF=OE﹣EF=10﹣4=6,
∴CF===8,
∴AB=CD=2CF=16,
即路面AB的宽度为16米.
故答案为:16.
16.解:设圆心为P,过点P作PE⊥AB于点E,PF⊥CD于点F,则EA=EB==4,FC=FD,
∴OE=EB﹣OB=4﹣2=2,
∴E(2,0),
设P(2,m),则F(0,m),
连接PC、PA,
在Rt△CPF中,PC2=(3﹣m)2+22,
在Rt△APE中,PA2=m2+42,
∵PA=PC,
∴(3﹣m)2+22=m2+42,
∴m=(舍正),
∴F(0,),
∴CF=DF==,
∴OD=OF+DF==4,
∴D(0,﹣4),
故答案为:(0,﹣4).
三.解答题(共5小题,满分40分)
17.(1)证明:∵OD⊥AB,OE⊥AC,
∴AD=AB,AE=AC,
∵AB=AC,
∴AD=AE,
∵∠ADO=∠A=∠AEO=90°,
∴四边形ADOE是正方形;
(2)解:连接OA,
∵AC=2cm,
∴AE=1cm,
在Rt△AOE中,OA==(cm),
答:⊙O的半径是cm.
18.解:连接DO并延长交AC于点E,
∵点D为弧ABC的中点,
∵DE⊥AC,且AE=EC,
AC=8,.AE=EC=4
∵DO=AO=5,
∴OE=3,
∴DE=8,
∴在Rt△DEC中,
DC==.
19.解:(1)∵OC⊥AB,
∴AD=BD;
(2)设主桥拱半径为R,由题意可知AB=26,CD=5,
∴BD=AB=13,
OD=OC﹣CD=R﹣5,
∵∠OBD=90°,
∴OD2+BD2=OB2,
∴(R﹣5)2+132=R2,
解得R=19.4≈19,
答:这座石拱桥主桥拱的半径约为19m.
20.(1)证明:如图:连接BD,
∵AB⊥CD于E,BF⊥AC于F,
∴∠CFG=∠GEB,
∵∠CGF=∠BGE,
∴∠C=∠GBE,
∵∠C=∠DBE,
∴∠GBE=∠DBE,
∵AB⊥CD于E,
∴∠GEB=∠DEB,
在△GBE和△DBE中,
,
∴△BGE≌△BDE(ASA),
∴ED=EG.
(2)解:如图:
连接OA,设OA=r,则DG=r+1,
由(1)可知ED=EG,
∴OE=,
∵AB⊥CD于E,AB=8,
∴AE=BE=4,
∴在Rt△OAE中,根据勾股定理得:OE2+AE2=OA2,
即()2+42=r2,
解得:r=,
即⊙O的半径为.
21.解:(1)如图1,过点O1作O1F⊥AB于F,并延长O1F交虚线劣弧AB于E,
∴AB=2AF,
由折叠知,EF=O1F=O1E=×4=2(cm),
连接O1A,
在Rt△O1FA中,O1A=4,
根据勾股定理得,AF===2(cm),
∴AB=2AF=4cm;
(2)如图2,延长O2C交虚线劣弧AB于G,
由折叠知,CG=CD,
∵D是O2C的中点,
∴CD=O2D,
∴CG=CD=O2D,
设⊙O2的半径为3rcm,则O2C=2r(cm),
∵O2C⊥弦AB,
∴AC=AB=5(cm),
连接O2A,
在Rt△ACO2中,根据勾股定理得,(3r)2﹣(2r)2=25,
∴r=(舍去负值),
∴O2A=3r=3(cm),
即⊙O2的半径为3cm.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
