2022-2023学年华东师大版八年级数学上册 12.3乘法公式 同步达标测试题 (Word版含答案)
文档属性
| 名称 | 2022-2023学年华东师大版八年级数学上册 12.3乘法公式 同步达标测试题 (Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 132.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-05 18:04:27 | ||
图片预览




文档简介
2022-2023学年华东师大版八年级数学上册《12.3乘法公式》同步达标测试题(附答案)
一.选择题(共10小题,满分30分)
1.下列各式中,不能用平方差公式计算的是( )
A.(x﹣y)(﹣y﹣x) B.(﹣x+y)(x﹣y)
C.(4x2﹣y2)(4x2+y2) D.(3x+1)(3x﹣1)
2.正方形的边长增加了2cm,面积相应增加了24cm2,则这个正方形原来的面积是( )
A.15cm2 B.25cm2 C.36cm2 D.49cm2
3.若x2+(a﹣1)x+25是一个完全平方式,则a值为( )
A.﹣9 B.﹣9或11 C.9或﹣11 D.11
4.计算得到( )
A. B. C. D.
5.计算(a+b﹣3)(a+b+3)的结果是( )
A.a2+b2﹣9 B.a2﹣b2+6b﹣9
C.a2+2ab+b2﹣9 D.a2﹣b2﹣6b+9
6.若一个正整数能表示为两个连续奇数的平方差,则称这个正整数为“好数”.下列正整数中能称为“好数”的是( )
A.205 B.250 C.502 D.520
7.如图,将长方形ABCD的各边向外作正方形,若四个正方形周长之和为24,面积之和为12,则长方形ABCD的面积为( )
A.4 B. C.5 D.6
8.计算(x+3y)2﹣(x﹣3y)2的结果是( )
A.12xy B.﹣12xy C.6xy D.﹣6xy
9.当x=1时,ax+b+1的值为﹣2,则(a+b﹣1)(1﹣a﹣b)的值为( )
A.16 B.8 C.﹣8 D.﹣16
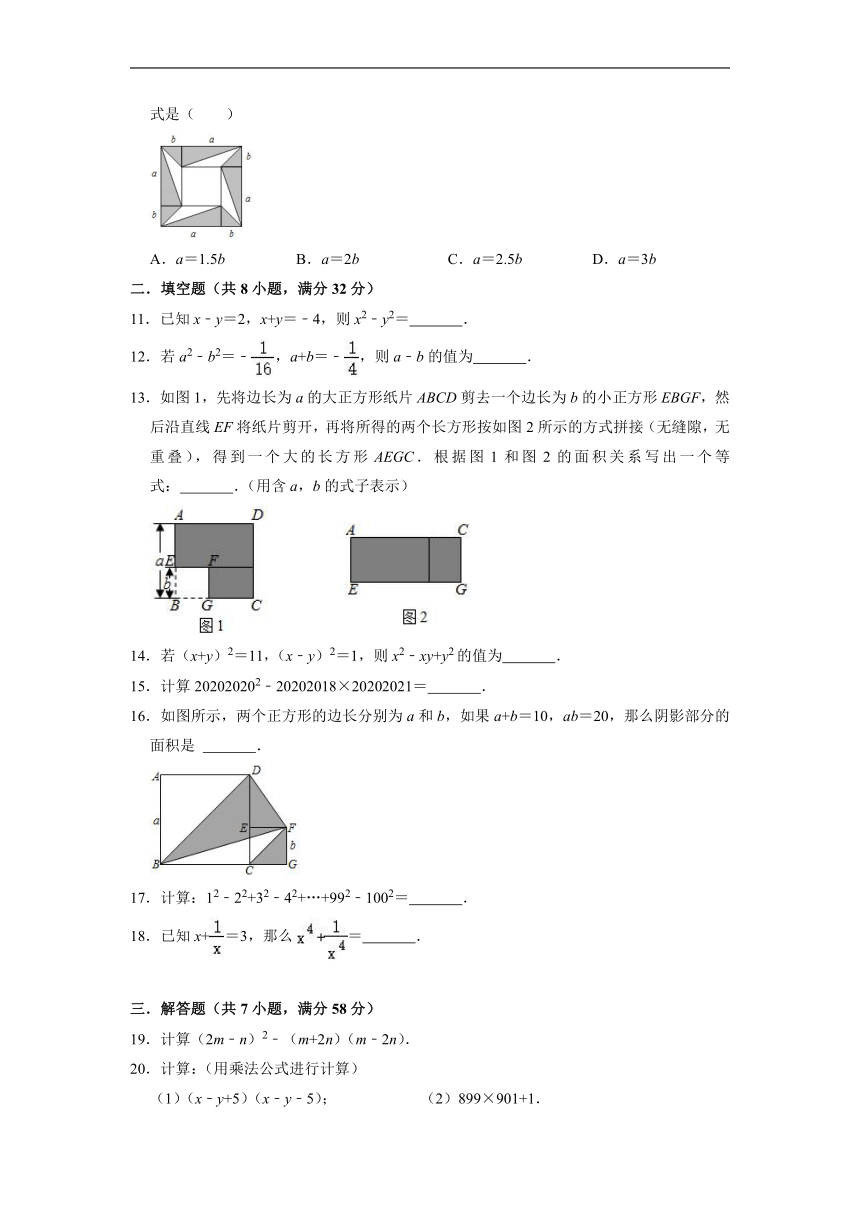
10.4张长为a,宽为b(a>b)的长方形纸片,按如图的方式拼成一个边长为(a+b)的正方形,图中空白部分的面积为S1,阴影部分的面积为S2,若S1=S2,则a,b满足的关系式是( )
A.a=1.5b B.a=2b C.a=2.5b D.a=3b
二.填空题(共8小题,满分32分)
11.已知x﹣y=2,x+y=﹣4,则x2﹣y2= .
12.若a2﹣b2=﹣,a+b=﹣,则a﹣b的值为 .
13.如图1,先将边长为a的大正方形纸片ABCD剪去一个边长为b的小正方形EBGF,然后沿直线EF将纸片剪开,再将所得的两个长方形按如图2所示的方式拼接(无缝隙,无重叠),得到一个大的长方形AEGC.根据图1和图2的面积关系写出一个等式: .(用含a,b的式子表示)
14.若(x+y)2=11,(x﹣y)2=1,则x2﹣xy+y2的值为 .
15.计算202020202﹣20202018×20202021= .
16.如图所示,两个正方形的边长分别为a和b,如果a+b=10,ab=20,那么阴影部分的面积是 .
17.计算:12﹣22+32﹣42+…+992﹣1002= .
18.已知x+=3,那么= .
三.解答题(共7小题,满分58分)
19.计算(2m﹣n)2﹣(m+2n)(m﹣2n).
20.计算:(用乘法公式进行计算)
(1)(x﹣y+5)(x﹣y﹣5); (2)899×901+1.
21.(1)如图,用四块完全相同的长方形拼成正方形,用不同的方法,计算图中阴影部分的面积,你能发现什么?(用含有x、y的等式表示) .
(2)若(3x﹣2y)2=5,(3x+2y)2=9,求xy的值;
(3)若2x+y=5,xy=2,求2x﹣y的值.
22.已知:x+y=3,xy=﹣1,求下列各式的值:
(1)x2+y2;
(2)(x﹣y)2.
23.【教材呈现】:图①,图②,图③分别是华东师大版八年级上册数学教材第33页、第34页和第52页的图形,结合图形解决下列问题:
(1)分别写出能够表示图①、图②中图形的面积关系的乘法公式: , .
(2)图③是用四个长和宽分别为a,b的全等长方形拼成的一个正方形(所拼图形无重叠、无缝隙),写出代数式(a+b)2、(a﹣b)2、ab之间的等量关系: .
【结论应用】根据上面(2)中探索的结论,回答下列问题:
(3)当m+n=5,mn=﹣1时,求m﹣n的值;
(4)设A=,B=m﹣3,化简(A+B)2﹣(A﹣B)2.
24.完全平方公式:(a±b)2=a2±2ab+b2适当的变形,可以解决很多的数学问题.
例如:若a+b=3,ab=1,求a2+b2的值.
解:因为a+b=3,ab=1
所以(a+b)2=9,2ab=2
所以a2+b2+2ab=9,2ab=2
得a2+b2=7
根据上面的解题思路与方法,解决下列问题:
(1)若x+y=8,x2+y2=40,求xy的值;
(2)请直接写出下列问题答案:
①若2a+b=5,ab=2,则2a﹣b= ;
②若(4﹣x)(5﹣x)=8,则(4﹣x)2+(5﹣x)2= .
(3)如图,点C是线段AB上的一点,以AC,BC为边向两边作正方形,设AB=6,两正方形的面积和S1+S2=18,求图中阴影部分面积.
25.观察下列各式:
1﹣=1﹣==×;
1﹣=1﹣==×;
1﹣=1﹣==×;
1﹣=1﹣==×;
…
(1)用你发现的规律填空:1﹣= × ,1﹣= × ;
(2)用你发现的规律进行计算:
(1﹣)×(1﹣)×(1﹣)×…×(1﹣)×(1﹣).
参考答案
一.选择题(共10小题,满分30分)
1.解:A、(x﹣y)(﹣y﹣x)=(﹣y+x)(﹣y﹣x)=(﹣y)2﹣x2=y2﹣x2,此题符合平方差公式的特征,能用平方差公式计算,故此选项不符合题意;
B、(﹣x+y)(x﹣y)=﹣(x﹣y)(x﹣y)=﹣(x﹣y)2=﹣x2+2xy﹣y2,此题不符合平方差公式的特征,不能用平方差公式计算,故此选项符合题意;
C、(4x2﹣y2)(4x2+y2)=(4x2)2﹣(y2)2=16x4﹣y4,原式能用平方差公式计算,故此选项不符合题意;
D、(3x+1)(3x﹣1)=(3x)2﹣12=9x2﹣1,原式能用平方差公式计算,故此选项不符合题意,
故选:B.
2.解:设正方形的边长是xcm,根据题意得:(x+2)2﹣x2=24,
解得:x=5.
则这个正方形原来的面积是25cm2,
故选:B.
3.解:x2+(a﹣1)x+25=x2+(a﹣1)x+52是完全平方式,则(a﹣1)x=±2 x 5,
解得:a=﹣9或11.
故选:B.
4.解:==.
故选:C.
5.解:原式=(a+b)2﹣9=a2+2ab+b2﹣9.
故选:C.
6.解:根据平方差公式得:
(2n+1)2﹣(2n﹣1)2=(2n+1+2n﹣1)(2n+1﹣2n+1)=4n×2=8n.
所以两个连续奇数构造的“好数”是8的倍数
205,250,502都不能被8整除,只有520能够被8整除.
故选:D.
7.解:设AB=a,AD=b,由题意得,
8a+8b=24,2a2+2b2=12,
即a+b=3,a2+b2=6,
∴ab===,
即长方形ABCD的面积为,
故选:B.
8.解:原式=x2+6xy+9y2﹣(x2﹣6xy+9y2)
=x2+6xy+9y2﹣x2+6xy﹣9y2
=12xy.
故选:A.
9.解:∵当x=1时,ax+b+1的值为﹣2,
∴a+b+1=﹣2,
∴a+b=﹣3,
∴(a+b﹣1)(1﹣a﹣b)=(﹣3﹣1)×(1+3)=﹣16.
故选:D.
10.解:由题意可得:
S2=4×b(a+b)
=2b(a+b);
S1=(a+b)2﹣S2
=(a+b)2﹣(2ab+2b2)
=a2+2ab+b2﹣2ab﹣2b2
=a2﹣b2;
∵S1=S2,
∴2b(a+b)=a2﹣b2,
∴2b(a+b)=(a﹣b)(a+b),
∵a+b>0,
∴2b=a﹣b,
∴a=3b.
故选:D.
二.填空题(共8小题,满分32分)
11.解:∵x﹣y=2,x+y=﹣4,
∴x2﹣y2=(x﹣y)(x+y)
=2×(﹣4)
=﹣8.
故答案为:﹣8.
12.解:因为a2﹣b2=﹣,
所以(a+b)(a﹣b)=﹣,
因为a+b=﹣,
所以a﹣b=﹣÷(﹣)=.
故答案为:.
13.解:图1中阴影部分的面积为:a2﹣b2,
图2中阴影部分的面积为:(a+b)(a﹣b),
因此有:a2﹣b2=(a+b)(a﹣b),
故答案为:a2﹣b2=(a+b)(a﹣b).
14.解:∵(x+y)2=x2+y2+2xy=11①,(x﹣y)2=x2+y2﹣2xy=1②,
∴①+②得:2(x2+y2)=12,即x2+y2=6,
①﹣②得:4xy=10,即xy=2.5,
则原式=6﹣2.5=3.5.
故答案为:3.5.
15.解:原式=202020202﹣(20202020﹣2)×(20202020+1)
=202020202﹣(202020202+20202020﹣40404040﹣2)
=202020202﹣202020202﹣20202020+40404040+2
=20202022,
故答案为:20202022.
16.解:由图可知,
五边形ABGFD的面积=正方形ABCD的面积+梯形DCGF的面积,
=a2+(a+b)b
=,
阴影部分的面积=五边形ABGFD的面积﹣三角形ABD﹣三角形BCF
=﹣﹣
=
=,
∵a+b=10,ab=20,
∴a2+b2=(a+b)2﹣2ab=102﹣2×20=60,
∴阴影部分的面积为=30.
故答案为:30.
17.解:原式=(12﹣22)+(32﹣42)+…+(992﹣1002)
=(1﹣2)(1+2)+(3﹣4)(3+4)+…+(99﹣100)(99+100)
=﹣(1+2)﹣(3+4)﹣…﹣(99+100)
=﹣(1+2+3+4+…+99+100)
=﹣5050.
故本题答案为:﹣5050.
18.解:∵x+=3,
∴x2+=(x+)2﹣2=7,
∴=(x2+)2﹣2=47.
三.解答题(共7小题,满分58分)
19.解:原式=4m2﹣4mn+n2﹣(m2﹣4n2)
=4m2﹣4mn+n2﹣m2+4n2
=3m2﹣4mn+5n2.
20.解:(1)原式=[(x﹣y)+5][(x﹣y)﹣5]
=(x﹣y)2﹣52
=x2﹣2xy+y2﹣25;
(2)原式=(900﹣1)(900+1)+1
=9002﹣1+1
=810000.
21.解:(1)4xy=(x+y)2﹣(x﹣y)2;
(2)∵(3x+2y)2﹣(3x﹣2y)2=24xy=9﹣5,
∴xy=;
(3)∵(2x+y)2﹣(2x﹣y)2=8xy,
∴25﹣16=(2x﹣y)2,
∴2x﹣y=±3.
22.解:(1)∵(x+y)2=x2+y2+2xy,x+y=3,xy=﹣1,
∴9=x2+y2﹣2,
∴x2+y2=11;
(2)∵x2+y2=11,
∴(x﹣y)2=x2+y2﹣2xy=11﹣2×(﹣1)=13.
23.解:(1)图①大正方形的边长为a+b,根据各个部分面积之间的关系可得,
(a+b)2=a2+2ab+b2,
图②中,最大的正方形的边长为a,较小的正方形的边长为a﹣b,最小的正方形的边长为b,根据各个部分面积之间的关系得,
(a﹣b)2=a2﹣2ab+b2,
故答案为:(a+b)2=a2+2ab+b2,(a﹣b)2=a2﹣2ab+b2;
(2)根据大正方形的面积等于小正方形面积与4个矩形面积的和可得,
(a+b)2=(a﹣b)2+4ab,
故答案为:(a+b)2=(a﹣b)2+4ab;
(3)由(2)可得,(m+n)2=(m﹣n)2+4mn,
∵m+n=5,mn=﹣1,
∴25=(m﹣n)2﹣4,
即(m﹣n)2=29,
∴m﹣n=±,
答:m﹣n的值为±;
(4)由完全平方公式得,
(A+B)2﹣(A﹣B)2=A2+2A B+B2﹣A2+2A B﹣B2=4A B,
当A=,B=m﹣3时,
原式=4××(m﹣3)=m2﹣9.
24.解:(1)∵(x+y)2﹣2xy=x2+y2,x+y=8,x2+y2=40,
∴82﹣2xy=40,
∴xy=12,
答:xy的值为12;
(2)①∵(2a﹣b)2=(2a+b)2﹣8ab,2a+b=5,ab=2,
∴(2a﹣b)2=52﹣8×2=9,
∴2a﹣b=±=±3,
故答案为:±3;
②根据a2+b2=(a﹣b)2+2ab可得,
(4﹣x)2+(5﹣x)2=[(4﹣x)﹣(5﹣x)]2+2(4﹣x)(5﹣x),
又∵(4﹣x)(5﹣x)=8,
∴(4﹣x)2+(5﹣x)2=(﹣1)2+2×8=17,
故答案为:17;
(3)设AC=m,CF=n,
∵AB=6,
∴m+n=6,
又∵S1+S2=18,
∴m2+n2=18,
由完全平方公式可得,(m+n)2=m2+2mn+n2,
∴62=18+2mn,
∴mn=9,
∴S阴影部分=mn=,
答:阴影部分的面积为.
25.解:(1)1﹣=(1﹣)×(1+)=,
1﹣=(1﹣)×(1+)=,
故答案为:,,,;
(2)原式=××××××…××××
=×
=.
一.选择题(共10小题,满分30分)
1.下列各式中,不能用平方差公式计算的是( )
A.(x﹣y)(﹣y﹣x) B.(﹣x+y)(x﹣y)
C.(4x2﹣y2)(4x2+y2) D.(3x+1)(3x﹣1)
2.正方形的边长增加了2cm,面积相应增加了24cm2,则这个正方形原来的面积是( )
A.15cm2 B.25cm2 C.36cm2 D.49cm2
3.若x2+(a﹣1)x+25是一个完全平方式,则a值为( )
A.﹣9 B.﹣9或11 C.9或﹣11 D.11
4.计算得到( )
A. B. C. D.
5.计算(a+b﹣3)(a+b+3)的结果是( )
A.a2+b2﹣9 B.a2﹣b2+6b﹣9
C.a2+2ab+b2﹣9 D.a2﹣b2﹣6b+9
6.若一个正整数能表示为两个连续奇数的平方差,则称这个正整数为“好数”.下列正整数中能称为“好数”的是( )
A.205 B.250 C.502 D.520
7.如图,将长方形ABCD的各边向外作正方形,若四个正方形周长之和为24,面积之和为12,则长方形ABCD的面积为( )
A.4 B. C.5 D.6
8.计算(x+3y)2﹣(x﹣3y)2的结果是( )
A.12xy B.﹣12xy C.6xy D.﹣6xy
9.当x=1时,ax+b+1的值为﹣2,则(a+b﹣1)(1﹣a﹣b)的值为( )
A.16 B.8 C.﹣8 D.﹣16
10.4张长为a,宽为b(a>b)的长方形纸片,按如图的方式拼成一个边长为(a+b)的正方形,图中空白部分的面积为S1,阴影部分的面积为S2,若S1=S2,则a,b满足的关系式是( )
A.a=1.5b B.a=2b C.a=2.5b D.a=3b
二.填空题(共8小题,满分32分)
11.已知x﹣y=2,x+y=﹣4,则x2﹣y2= .
12.若a2﹣b2=﹣,a+b=﹣,则a﹣b的值为 .
13.如图1,先将边长为a的大正方形纸片ABCD剪去一个边长为b的小正方形EBGF,然后沿直线EF将纸片剪开,再将所得的两个长方形按如图2所示的方式拼接(无缝隙,无重叠),得到一个大的长方形AEGC.根据图1和图2的面积关系写出一个等式: .(用含a,b的式子表示)
14.若(x+y)2=11,(x﹣y)2=1,则x2﹣xy+y2的值为 .
15.计算202020202﹣20202018×20202021= .
16.如图所示,两个正方形的边长分别为a和b,如果a+b=10,ab=20,那么阴影部分的面积是 .
17.计算:12﹣22+32﹣42+…+992﹣1002= .
18.已知x+=3,那么= .
三.解答题(共7小题,满分58分)
19.计算(2m﹣n)2﹣(m+2n)(m﹣2n).
20.计算:(用乘法公式进行计算)
(1)(x﹣y+5)(x﹣y﹣5); (2)899×901+1.
21.(1)如图,用四块完全相同的长方形拼成正方形,用不同的方法,计算图中阴影部分的面积,你能发现什么?(用含有x、y的等式表示) .
(2)若(3x﹣2y)2=5,(3x+2y)2=9,求xy的值;
(3)若2x+y=5,xy=2,求2x﹣y的值.
22.已知:x+y=3,xy=﹣1,求下列各式的值:
(1)x2+y2;
(2)(x﹣y)2.
23.【教材呈现】:图①,图②,图③分别是华东师大版八年级上册数学教材第33页、第34页和第52页的图形,结合图形解决下列问题:
(1)分别写出能够表示图①、图②中图形的面积关系的乘法公式: , .
(2)图③是用四个长和宽分别为a,b的全等长方形拼成的一个正方形(所拼图形无重叠、无缝隙),写出代数式(a+b)2、(a﹣b)2、ab之间的等量关系: .
【结论应用】根据上面(2)中探索的结论,回答下列问题:
(3)当m+n=5,mn=﹣1时,求m﹣n的值;
(4)设A=,B=m﹣3,化简(A+B)2﹣(A﹣B)2.
24.完全平方公式:(a±b)2=a2±2ab+b2适当的变形,可以解决很多的数学问题.
例如:若a+b=3,ab=1,求a2+b2的值.
解:因为a+b=3,ab=1
所以(a+b)2=9,2ab=2
所以a2+b2+2ab=9,2ab=2
得a2+b2=7
根据上面的解题思路与方法,解决下列问题:
(1)若x+y=8,x2+y2=40,求xy的值;
(2)请直接写出下列问题答案:
①若2a+b=5,ab=2,则2a﹣b= ;
②若(4﹣x)(5﹣x)=8,则(4﹣x)2+(5﹣x)2= .
(3)如图,点C是线段AB上的一点,以AC,BC为边向两边作正方形,设AB=6,两正方形的面积和S1+S2=18,求图中阴影部分面积.
25.观察下列各式:
1﹣=1﹣==×;
1﹣=1﹣==×;
1﹣=1﹣==×;
1﹣=1﹣==×;
…
(1)用你发现的规律填空:1﹣= × ,1﹣= × ;
(2)用你发现的规律进行计算:
(1﹣)×(1﹣)×(1﹣)×…×(1﹣)×(1﹣).
参考答案
一.选择题(共10小题,满分30分)
1.解:A、(x﹣y)(﹣y﹣x)=(﹣y+x)(﹣y﹣x)=(﹣y)2﹣x2=y2﹣x2,此题符合平方差公式的特征,能用平方差公式计算,故此选项不符合题意;
B、(﹣x+y)(x﹣y)=﹣(x﹣y)(x﹣y)=﹣(x﹣y)2=﹣x2+2xy﹣y2,此题不符合平方差公式的特征,不能用平方差公式计算,故此选项符合题意;
C、(4x2﹣y2)(4x2+y2)=(4x2)2﹣(y2)2=16x4﹣y4,原式能用平方差公式计算,故此选项不符合题意;
D、(3x+1)(3x﹣1)=(3x)2﹣12=9x2﹣1,原式能用平方差公式计算,故此选项不符合题意,
故选:B.
2.解:设正方形的边长是xcm,根据题意得:(x+2)2﹣x2=24,
解得:x=5.
则这个正方形原来的面积是25cm2,
故选:B.
3.解:x2+(a﹣1)x+25=x2+(a﹣1)x+52是完全平方式,则(a﹣1)x=±2 x 5,
解得:a=﹣9或11.
故选:B.
4.解:==.
故选:C.
5.解:原式=(a+b)2﹣9=a2+2ab+b2﹣9.
故选:C.
6.解:根据平方差公式得:
(2n+1)2﹣(2n﹣1)2=(2n+1+2n﹣1)(2n+1﹣2n+1)=4n×2=8n.
所以两个连续奇数构造的“好数”是8的倍数
205,250,502都不能被8整除,只有520能够被8整除.
故选:D.
7.解:设AB=a,AD=b,由题意得,
8a+8b=24,2a2+2b2=12,
即a+b=3,a2+b2=6,
∴ab===,
即长方形ABCD的面积为,
故选:B.
8.解:原式=x2+6xy+9y2﹣(x2﹣6xy+9y2)
=x2+6xy+9y2﹣x2+6xy﹣9y2
=12xy.
故选:A.
9.解:∵当x=1时,ax+b+1的值为﹣2,
∴a+b+1=﹣2,
∴a+b=﹣3,
∴(a+b﹣1)(1﹣a﹣b)=(﹣3﹣1)×(1+3)=﹣16.
故选:D.
10.解:由题意可得:
S2=4×b(a+b)
=2b(a+b);
S1=(a+b)2﹣S2
=(a+b)2﹣(2ab+2b2)
=a2+2ab+b2﹣2ab﹣2b2
=a2﹣b2;
∵S1=S2,
∴2b(a+b)=a2﹣b2,
∴2b(a+b)=(a﹣b)(a+b),
∵a+b>0,
∴2b=a﹣b,
∴a=3b.
故选:D.
二.填空题(共8小题,满分32分)
11.解:∵x﹣y=2,x+y=﹣4,
∴x2﹣y2=(x﹣y)(x+y)
=2×(﹣4)
=﹣8.
故答案为:﹣8.
12.解:因为a2﹣b2=﹣,
所以(a+b)(a﹣b)=﹣,
因为a+b=﹣,
所以a﹣b=﹣÷(﹣)=.
故答案为:.
13.解:图1中阴影部分的面积为:a2﹣b2,
图2中阴影部分的面积为:(a+b)(a﹣b),
因此有:a2﹣b2=(a+b)(a﹣b),
故答案为:a2﹣b2=(a+b)(a﹣b).
14.解:∵(x+y)2=x2+y2+2xy=11①,(x﹣y)2=x2+y2﹣2xy=1②,
∴①+②得:2(x2+y2)=12,即x2+y2=6,
①﹣②得:4xy=10,即xy=2.5,
则原式=6﹣2.5=3.5.
故答案为:3.5.
15.解:原式=202020202﹣(20202020﹣2)×(20202020+1)
=202020202﹣(202020202+20202020﹣40404040﹣2)
=202020202﹣202020202﹣20202020+40404040+2
=20202022,
故答案为:20202022.
16.解:由图可知,
五边形ABGFD的面积=正方形ABCD的面积+梯形DCGF的面积,
=a2+(a+b)b
=,
阴影部分的面积=五边形ABGFD的面积﹣三角形ABD﹣三角形BCF
=﹣﹣
=
=,
∵a+b=10,ab=20,
∴a2+b2=(a+b)2﹣2ab=102﹣2×20=60,
∴阴影部分的面积为=30.
故答案为:30.
17.解:原式=(12﹣22)+(32﹣42)+…+(992﹣1002)
=(1﹣2)(1+2)+(3﹣4)(3+4)+…+(99﹣100)(99+100)
=﹣(1+2)﹣(3+4)﹣…﹣(99+100)
=﹣(1+2+3+4+…+99+100)
=﹣5050.
故本题答案为:﹣5050.
18.解:∵x+=3,
∴x2+=(x+)2﹣2=7,
∴=(x2+)2﹣2=47.
三.解答题(共7小题,满分58分)
19.解:原式=4m2﹣4mn+n2﹣(m2﹣4n2)
=4m2﹣4mn+n2﹣m2+4n2
=3m2﹣4mn+5n2.
20.解:(1)原式=[(x﹣y)+5][(x﹣y)﹣5]
=(x﹣y)2﹣52
=x2﹣2xy+y2﹣25;
(2)原式=(900﹣1)(900+1)+1
=9002﹣1+1
=810000.
21.解:(1)4xy=(x+y)2﹣(x﹣y)2;
(2)∵(3x+2y)2﹣(3x﹣2y)2=24xy=9﹣5,
∴xy=;
(3)∵(2x+y)2﹣(2x﹣y)2=8xy,
∴25﹣16=(2x﹣y)2,
∴2x﹣y=±3.
22.解:(1)∵(x+y)2=x2+y2+2xy,x+y=3,xy=﹣1,
∴9=x2+y2﹣2,
∴x2+y2=11;
(2)∵x2+y2=11,
∴(x﹣y)2=x2+y2﹣2xy=11﹣2×(﹣1)=13.
23.解:(1)图①大正方形的边长为a+b,根据各个部分面积之间的关系可得,
(a+b)2=a2+2ab+b2,
图②中,最大的正方形的边长为a,较小的正方形的边长为a﹣b,最小的正方形的边长为b,根据各个部分面积之间的关系得,
(a﹣b)2=a2﹣2ab+b2,
故答案为:(a+b)2=a2+2ab+b2,(a﹣b)2=a2﹣2ab+b2;
(2)根据大正方形的面积等于小正方形面积与4个矩形面积的和可得,
(a+b)2=(a﹣b)2+4ab,
故答案为:(a+b)2=(a﹣b)2+4ab;
(3)由(2)可得,(m+n)2=(m﹣n)2+4mn,
∵m+n=5,mn=﹣1,
∴25=(m﹣n)2﹣4,
即(m﹣n)2=29,
∴m﹣n=±,
答:m﹣n的值为±;
(4)由完全平方公式得,
(A+B)2﹣(A﹣B)2=A2+2A B+B2﹣A2+2A B﹣B2=4A B,
当A=,B=m﹣3时,
原式=4××(m﹣3)=m2﹣9.
24.解:(1)∵(x+y)2﹣2xy=x2+y2,x+y=8,x2+y2=40,
∴82﹣2xy=40,
∴xy=12,
答:xy的值为12;
(2)①∵(2a﹣b)2=(2a+b)2﹣8ab,2a+b=5,ab=2,
∴(2a﹣b)2=52﹣8×2=9,
∴2a﹣b=±=±3,
故答案为:±3;
②根据a2+b2=(a﹣b)2+2ab可得,
(4﹣x)2+(5﹣x)2=[(4﹣x)﹣(5﹣x)]2+2(4﹣x)(5﹣x),
又∵(4﹣x)(5﹣x)=8,
∴(4﹣x)2+(5﹣x)2=(﹣1)2+2×8=17,
故答案为:17;
(3)设AC=m,CF=n,
∵AB=6,
∴m+n=6,
又∵S1+S2=18,
∴m2+n2=18,
由完全平方公式可得,(m+n)2=m2+2mn+n2,
∴62=18+2mn,
∴mn=9,
∴S阴影部分=mn=,
答:阴影部分的面积为.
25.解:(1)1﹣=(1﹣)×(1+)=,
1﹣=(1﹣)×(1+)=,
故答案为:,,,;
(2)原式=××××××…××××
=×
=.
