2022-2023学年人教版九年级数学上册 24.2.1 点和圆的位置关系同步练习(Word版含答案)
文档属性
| 名称 | 2022-2023学年人教版九年级数学上册 24.2.1 点和圆的位置关系同步练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 481.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-05 18:08:08 | ||
图片预览


文档简介
人教版九上 24.2.1 点和圆的位置关系
一、选择题(共7小题)
1. 的半径为 ,点 到圆心 的距离 ,则点 与圆 的位置关系为
A. 点 在圆上 B. 点 在圆内 C. 点 在圆外 D. 无法确定
2. 如图所示,在 的正方形网格中,一条圆弧经过 ,, 三点,那么这条圆弧所在圆的圆心是
A. 点 B. 点 C. 点 D. 点
3. 下列说法中,正确的个数是
①任何三角形有且只有一个外接圆;
②任何圆有且只有一个内接三角形;
③三角形的外心不一定在三角形内部;
④三角形的外心到三角形三边的距离相等;
⑤经过三点可确定一个圆.
A. B. C. D.
4. 用反证法证明命题“四边形四个内角中至少有一个角大于等于 ”,我们应该假设
A. 四个角都小于 B. 最多有一个角大于或等于
C. 有两个角小于 D. 四个角都大于或等于
5. 在公园的 处附近有 ,,, 四棵树,位置如图所示(图中小正方形的边长均相等),现计划修建一座以点 为圆心, 长为半径的圆形水池,要求池内不留树木,则 ,,, 四棵树中需要被移除的为
A. ,, B. ,, C. ,, D. ,,
6. 若⊙所在平面内一点到⊙上的点的最大距离为,最小距离为,则此圆的半径为
A. B. C. 或 D. 或
7. 已知点 是 的外心,作正方形 ,下列说法:
①点 是 的外心;
②点 是 的外心;
③点 是 的外心;
④点 是 的外心.
其中一定不成立的说法是
A. ②④ B. ①③ C. ②③④ D. ①③④
二、填空题(共7小题)
8. 若圆 的半径是 ,圆心的坐标是 ,点 的坐标是 ,则点 与 的位置关系是 .
9. 如图.在 中,,.能够将 完全覆盖的最小圆形纸片的直径是 .
10. 在 中,,若 ,,则 的外接圆 的半径 为 .
11. 已知 的三边长分别是 ,,,则 外接圆的直径是 .
12. 如图,,, 是 上的三个点,若 ,则 .
13. 正方形 的边长是 ,对角线 , 相交于点 ,若以 为圆心作圆要使点 在 外,则所选取的半径 的取值范围是 .
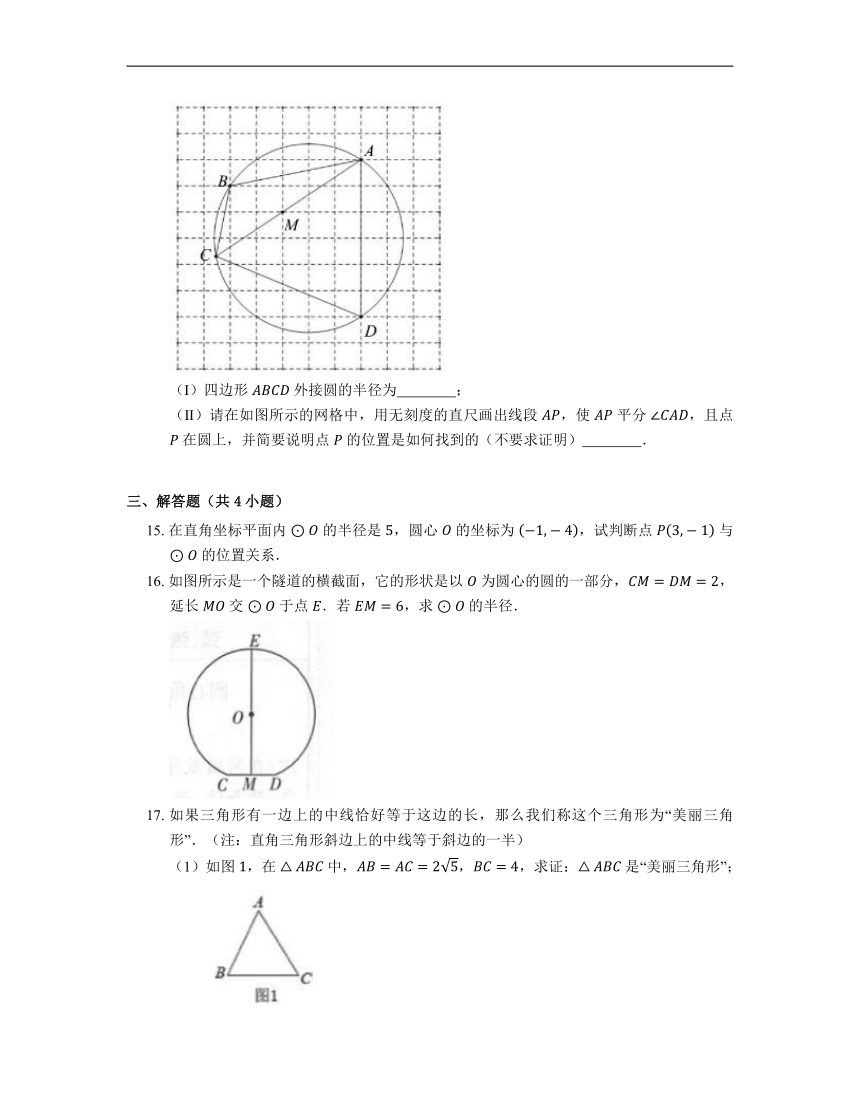
14. 如图,在每个小正方形的边长为 的网格中,点 ,点 ,点 均在格点上,并且在同一个圆上,取格点 ,连接 并延长交圆于点 .
(Ⅰ)四边形 外接圆的半径为 ;
(Ⅱ)请在如图所示的网格中,用无刻度的直尺画出线段 ,使 平分 ,且点 在圆上,并简要说明点 的位置是如何找到的(不要求证明) .
三、解答题(共4小题)
15. 在直角坐标平面内 的半径是 ,圆心 的坐标为 ,试判断点 与 的位置关系.
16. 如图所示是一个隧道的横截面,它的形状是以 为圆心的圆的一部分,,延长 交 于点 .若 ,求 的半径.
17. 如果三角形有一边上的中线恰好等于这边的长,那么我们称这个三角形为“美丽三角形”.(注:直角三角形斜边上的中线等于斜边的一半)
(1)如图 ,在 中,,,求证: 是“美丽三角形”;
(2)如图 ,在 中,,,若 是“美丽三角形”,求 的长.
18. 已知 的面积为 , 为平面内一点.
(1)若 ,则点 在 .
(2)若 ,则点 在 .
(3)若 ,则点 在 上.
答案
1. B
2. C
3. B
【解析】①③正确.任何一个圆都有无数个内接三角形故②错;三角形的外心到三角形的三个顶点的距离相等,故④错;经过不在同一直线上的三点可确定一个圆,故⑤错.
4. A
【解析】用反证法证明“四边形的四个内角中至少有一个不小于 ”时第一步应假设:四个角都小于 度.
5. A
6. C
【解析】【分析】搞清⊙所在平面内一点到⊙上的点的最大距离、最小距离的差或和为⊙的直径,即可求解.
【解析】解:若⊙所在平面内一点到⊙上的点的最大距离为,最小距离为,若这个点在圆的内部或在圆上时时,圆的直径是,因而半径是;当此点在圆外时,圆的直径是,因而半径是.则此圆的半径为或.
故选:.
【点评】注意到分两种情况进行讨论是解决本题的关键.
7. A 【解析】连接 ,,,
为锐角三角形 的外心,
,
四边形 为正方形,
,
,
,即 不是 的外心,
,即 是 的外心,
,即 是 的外心,
,即 不是 的外心.
8. 点 在圆 上
【解析】 点 的坐标是 ,
,
等于圆 的半径,
点 在圆 上.
9.
10.
11.
【解析】如图,
,,,
,
,
的外接圆的半径是 ,即外接圆的直径是 .
12.
【解析】如图,在优弧 上取点 ,连接 ,,
,
,
.
13.
14. ,取格点 ,,连接 ,交 于点 .取格点 ,连接 并延长交圆于点 ,连接 , 即为所求.
15. 点 在 上.
16. 如图,连接 .
,
.
设 的半径是 .
,
.
在 中,,
即 .
解得 .
的半径是 .
17. (1) 如图,过点 作 于 ,
因为 ,,,
所以 ,
又因为 ,
所以由勾股定理得,,
所以 ,
所以 是“美丽三角形”.
(2) 如图,作中线 ,,
当 边上的中线 时,
因为 ,点 为 的中点,
所以 ,,
所以 ,
当 边上的中线 时,
则 ,
由勾股定理得:,
即 ,
解得:(舍负).
综上所述, 的长是 或 .
18. (1) 外
【解析】 的面积为 ,
的半径为 .
,
点 在 外.
(2) 内
(3)
一、选择题(共7小题)
1. 的半径为 ,点 到圆心 的距离 ,则点 与圆 的位置关系为
A. 点 在圆上 B. 点 在圆内 C. 点 在圆外 D. 无法确定
2. 如图所示,在 的正方形网格中,一条圆弧经过 ,, 三点,那么这条圆弧所在圆的圆心是
A. 点 B. 点 C. 点 D. 点
3. 下列说法中,正确的个数是
①任何三角形有且只有一个外接圆;
②任何圆有且只有一个内接三角形;
③三角形的外心不一定在三角形内部;
④三角形的外心到三角形三边的距离相等;
⑤经过三点可确定一个圆.
A. B. C. D.
4. 用反证法证明命题“四边形四个内角中至少有一个角大于等于 ”,我们应该假设
A. 四个角都小于 B. 最多有一个角大于或等于
C. 有两个角小于 D. 四个角都大于或等于
5. 在公园的 处附近有 ,,, 四棵树,位置如图所示(图中小正方形的边长均相等),现计划修建一座以点 为圆心, 长为半径的圆形水池,要求池内不留树木,则 ,,, 四棵树中需要被移除的为
A. ,, B. ,, C. ,, D. ,,
6. 若⊙所在平面内一点到⊙上的点的最大距离为,最小距离为,则此圆的半径为
A. B. C. 或 D. 或
7. 已知点 是 的外心,作正方形 ,下列说法:
①点 是 的外心;
②点 是 的外心;
③点 是 的外心;
④点 是 的外心.
其中一定不成立的说法是
A. ②④ B. ①③ C. ②③④ D. ①③④
二、填空题(共7小题)
8. 若圆 的半径是 ,圆心的坐标是 ,点 的坐标是 ,则点 与 的位置关系是 .
9. 如图.在 中,,.能够将 完全覆盖的最小圆形纸片的直径是 .
10. 在 中,,若 ,,则 的外接圆 的半径 为 .
11. 已知 的三边长分别是 ,,,则 外接圆的直径是 .
12. 如图,,, 是 上的三个点,若 ,则 .
13. 正方形 的边长是 ,对角线 , 相交于点 ,若以 为圆心作圆要使点 在 外,则所选取的半径 的取值范围是 .
14. 如图,在每个小正方形的边长为 的网格中,点 ,点 ,点 均在格点上,并且在同一个圆上,取格点 ,连接 并延长交圆于点 .
(Ⅰ)四边形 外接圆的半径为 ;
(Ⅱ)请在如图所示的网格中,用无刻度的直尺画出线段 ,使 平分 ,且点 在圆上,并简要说明点 的位置是如何找到的(不要求证明) .
三、解答题(共4小题)
15. 在直角坐标平面内 的半径是 ,圆心 的坐标为 ,试判断点 与 的位置关系.
16. 如图所示是一个隧道的横截面,它的形状是以 为圆心的圆的一部分,,延长 交 于点 .若 ,求 的半径.
17. 如果三角形有一边上的中线恰好等于这边的长,那么我们称这个三角形为“美丽三角形”.(注:直角三角形斜边上的中线等于斜边的一半)
(1)如图 ,在 中,,,求证: 是“美丽三角形”;
(2)如图 ,在 中,,,若 是“美丽三角形”,求 的长.
18. 已知 的面积为 , 为平面内一点.
(1)若 ,则点 在 .
(2)若 ,则点 在 .
(3)若 ,则点 在 上.
答案
1. B
2. C
3. B
【解析】①③正确.任何一个圆都有无数个内接三角形故②错;三角形的外心到三角形的三个顶点的距离相等,故④错;经过不在同一直线上的三点可确定一个圆,故⑤错.
4. A
【解析】用反证法证明“四边形的四个内角中至少有一个不小于 ”时第一步应假设:四个角都小于 度.
5. A
6. C
【解析】【分析】搞清⊙所在平面内一点到⊙上的点的最大距离、最小距离的差或和为⊙的直径,即可求解.
【解析】解:若⊙所在平面内一点到⊙上的点的最大距离为,最小距离为,若这个点在圆的内部或在圆上时时,圆的直径是,因而半径是;当此点在圆外时,圆的直径是,因而半径是.则此圆的半径为或.
故选:.
【点评】注意到分两种情况进行讨论是解决本题的关键.
7. A 【解析】连接 ,,,
为锐角三角形 的外心,
,
四边形 为正方形,
,
,
,即 不是 的外心,
,即 是 的外心,
,即 是 的外心,
,即 不是 的外心.
8. 点 在圆 上
【解析】 点 的坐标是 ,
,
等于圆 的半径,
点 在圆 上.
9.
10.
11.
【解析】如图,
,,,
,
,
的外接圆的半径是 ,即外接圆的直径是 .
12.
【解析】如图,在优弧 上取点 ,连接 ,,
,
,
.
13.
14. ,取格点 ,,连接 ,交 于点 .取格点 ,连接 并延长交圆于点 ,连接 , 即为所求.
15. 点 在 上.
16. 如图,连接 .
,
.
设 的半径是 .
,
.
在 中,,
即 .
解得 .
的半径是 .
17. (1) 如图,过点 作 于 ,
因为 ,,,
所以 ,
又因为 ,
所以由勾股定理得,,
所以 ,
所以 是“美丽三角形”.
(2) 如图,作中线 ,,
当 边上的中线 时,
因为 ,点 为 的中点,
所以 ,,
所以 ,
当 边上的中线 时,
则 ,
由勾股定理得:,
即 ,
解得:(舍负).
综上所述, 的长是 或 .
18. (1) 外
【解析】 的面积为 ,
的半径为 .
,
点 在 外.
(2) 内
(3)
同课章节目录
