2022-2023学年北师大版数学九年级上册 第四章 图形的相似同步练习(Word版含答案)
文档属性
| 名称 | 2022-2023学年北师大版数学九年级上册 第四章 图形的相似同步练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-06 06:46:45 | ||
图片预览

文档简介
第四章 图形的相似
一、选择题:(共10小题)
1.在比例尺是1:38 000的黄浦江交通游览图上,某隧道长约7cm,它的实际长度约为( )
A.266 km B.26.6km C.2.66km D.0.266km
2.如图,已知都与垂直,垂足分别是,且,那么的长是( )
A. B. C. D.
3.如图,在中,D、E分别为线段BC、BA的中点,设的面积为,的面积为.则( )
A. B. C. D.
4.如图,在中,,,则的长为
( )
A.6 B.8 C.10 D.12
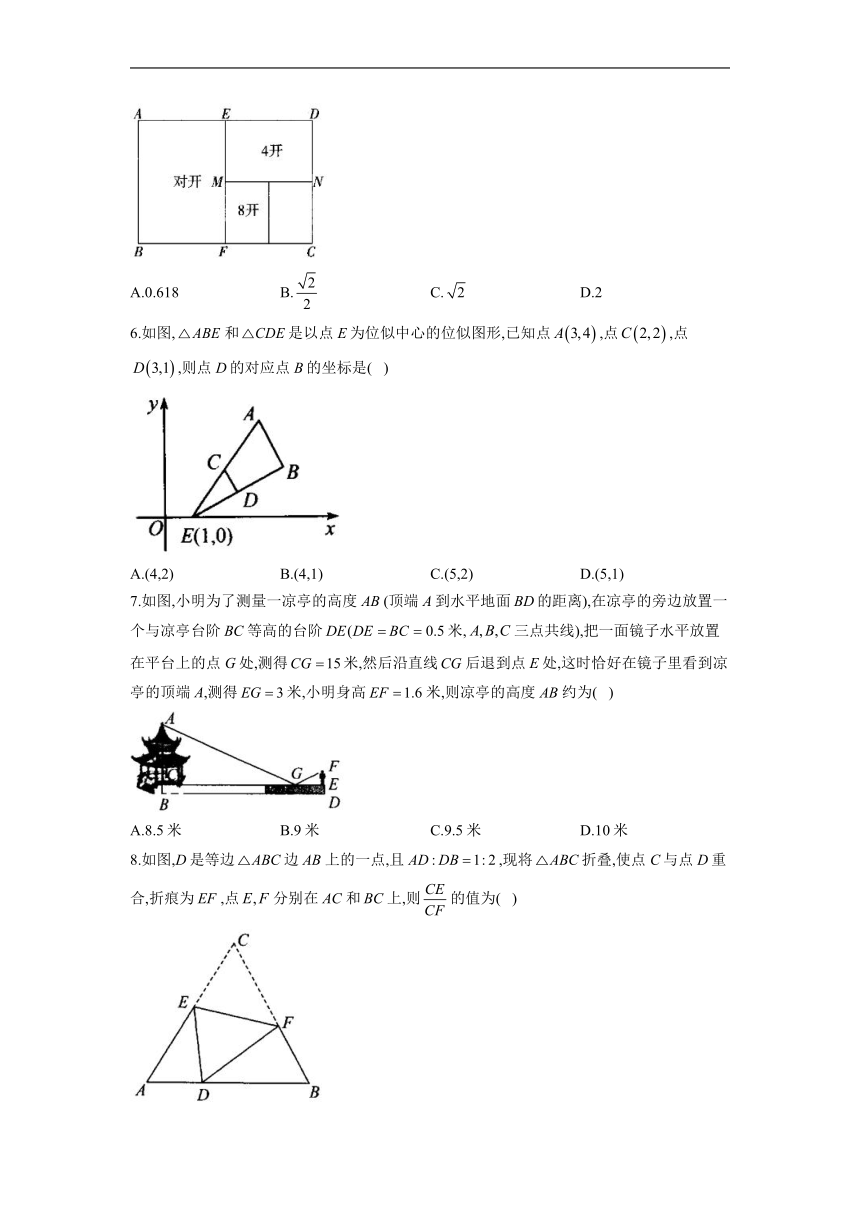
5.如图所示,一般书本的纸张是由原纸张多次对开得到的,矩形ABCD沿EF对开后,再把矩形EFCD沿MN对开,依次类推,若各种开本的矩形都相似,则等于( )
A.0.618 B. C. D.2
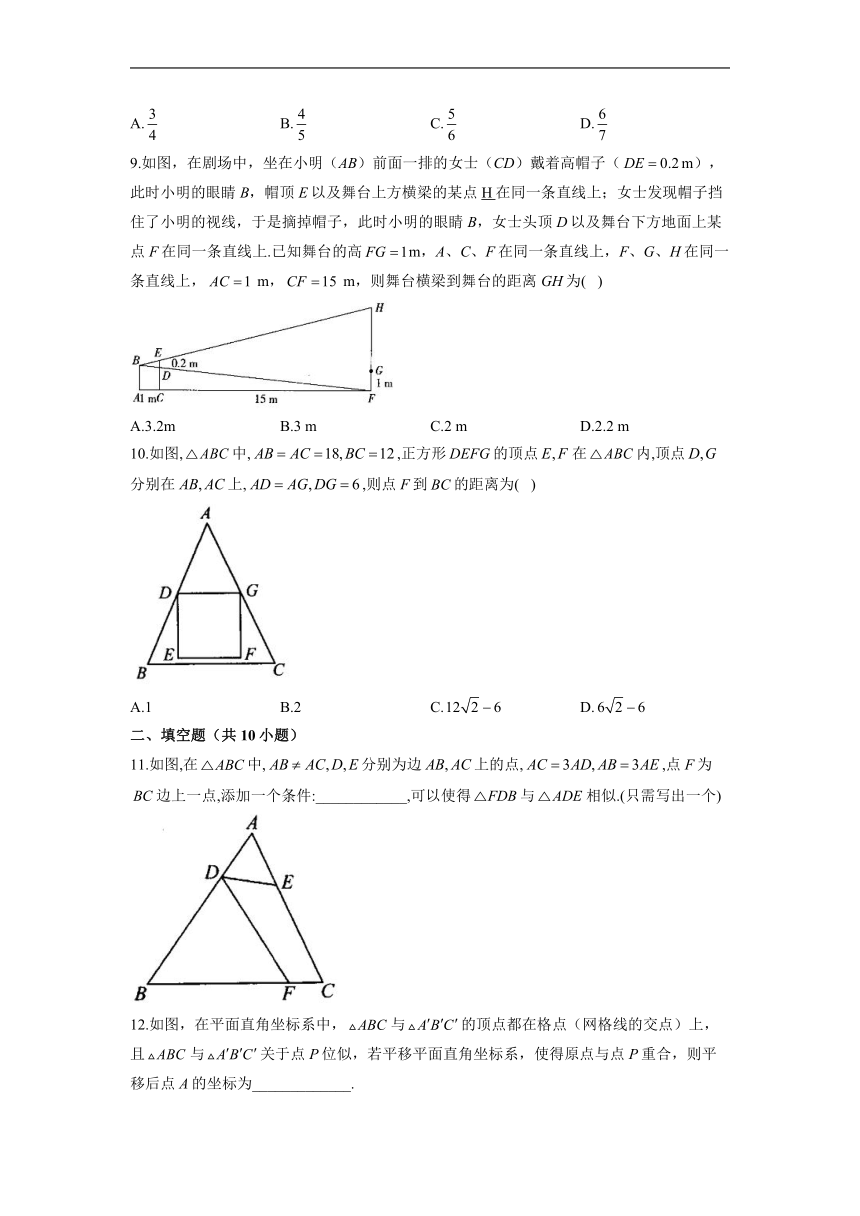
6.如图,和是以点E为位似中心的位似图形,已知点,点,点,则点D的对应点B的坐标是( )
A.(4,2) B.(4,1) C.(5,2) D.(5,1)
7.如图,小明为了测量一凉亭的高度(顶端A到水平地面的距离),在凉亭的旁边放置一个与凉亭台阶等高的台阶米,三点共线),把一面镜子水平放置在平台上的点G处,测得米,然后沿直线后退到点E处,这时恰好在镜子里看到凉亭的顶端A,测得米,小明身高米,则凉亭的高度约为( )
A.8.5米 B.9米 C.9.5米 D.10米
8.如图,D是等边边上的一点,且,现将折叠,使点C与点D重合,折痕为,点分别在和上,则的值为( )
A. B. C. D.
9.如图,在剧场中,坐在小明(AB)前面一排的女士(CD)戴着高帽子(m),此时小明的眼睛B,帽顶E以及舞台上方横梁的某点H在同一条直线上;女士发现帽子挡住了小明的视线,于是摘掉帽子,此时小明的眼睛B,女士头顶D以及舞台下方地面上某点F在同一条直线上.已知舞台的高m,A、C、F在同一条直线上,F、G、H在同一条直线上, m, m,则舞台横梁到舞台的距离GH为( )
A.3.2m B.3 m C.2 m D.2.2 m
10.如图,中,,正方形的顶点在内,顶点分别在上,,则点F到的距离为( )
A.1 B.2 C. D.
二、填空题(共10小题)
11.如图,在中,分别为边上的点,,点F为边上一点,添加一个条件:____________,可以使得与相似.(只需写出一个)
12.如图,在平面直角坐标系中,与的顶点都在格点(网格线的交点)上,且与关于点P位似,若平移平面直角坐标系,使得原点与点P重合,则平移后点A的坐标为_____________.
13.如图,在中,,点D在边上,于点E,连接,则的面积等于________.
14.如图,,点在上,与交于点,,则的长为__________.
15.如图,在中,,点F在边上,且,点E为边上的动点,将沿直线翻折,点C落在点P处,则点P到边距离的最小值是_________.
三、解答题(共6小题)
16.如图,已知是直角坐标系平面上三点.
(1)把向右平移4个单位再向下平移1个单位,得到.画出平移后的图形,并写出点A的对应点的坐标;
(2)以原点O为位似中心,将的周长缩小为原来的一半,得到,请在所给的坐标系中作出所有满足条件的图形.
17.如图,在平行四边形中,F是边的中点,延长,与延长线相交于点E,连接.
(1)求证:;
(2)若平分,请判断并证明四边形的形状.
18.如图,在相对的两栋楼中间有一堵墙,甲、乙两人分别在这两栋楼内观察这堵墙,视线如图1所示.根据实际情况画出平面图形如图2(),甲从点C可以看到点G处,乙从点E可以看到点D处,点B是的中点,墙高5.5米,米,米,求甲、乙两人的观测点到地面的距离之差(结果精确到0.1米).
19.如图,已知四边形是平行四边形,点E在边的延长线上,交于点F,.
(1)求证:;
(2)若,求的值.
20.根据相似多边形的定义,我们把四个角分别相等,四条边成比例的两个凸四边形叫做相似四边形.相似四边形对应边的比叫做相似比.
(1)某同学在探究相似四边形的判定时,得到如下三个命题,请判断它们是否正确(直接在横线上填写“真”或“假”).
(ⅰ)各边成比例的两个凸四边形相似;(_________命题)
(ⅱ)三个角分别相等的两个凸四边形相似;(________命题)
(ⅲ)两个大小不同的正方形相似;(_________命题)
(2)如图①,在四边形ABCD和四边形中,,,.求证:四边形ABCD与四边形相似;
(3)如图②,四边形ABCD中,,AC与BD相交于点O,过点O作分别交AD,BC于点E,F.记四边形ABFE的面积为,四边形EFCD的面积为,若四边形与四边形EFCD相似,求的值.
21.问题提出
如图(1),在中,,D是AC的中点,延长BC至点E,使,延长ED交AB于点F,探究的值.
问题探究
(1)先将问题特殊化.如图(2),当时,直接写出的值;
(2)再探究一般情形.如图(1),证明(1)中的结论仍然成立.
问题拓展
如图(3),在中,,D是AC的中点,G是边BC上一点,(),延长BC至点E,使,延长ED交AB于点F.直接写出的值(用含n的式子表示).
答案以及解析
1.答案:C
解析:设隧道的实际长度是,根据题意得,解得,.
2.答案:C
解析:都与垂直,
,
,
.
同理,
,
,故选C.
3.答案:B
解析:在中,D、E分别为线段BC、BA的中点,DE为的中位线,,,,,,即,故选:B.
4.答案:C
解析:,四边形是平行四边形,,,故选C.
5.答案:C
解析:由题意得,且,,即,.故选C.
6.答案:C
解析:设点B的坐标为.
和是以点E为位似中心的位似图形,
,
解得点B的坐标为(5,2).故选C.
7.答案:A
解析:由题意可知.
又,
,
,
,
米,
(米).
8.答案:B
解析:由折叠可知,
所以.
在中,因为,
所以,
所以.
又因为,
所以,
所以.
设,
则,
则,
取,可得,①
取,可得,②
①+②得,即,
由比例的基本性质可得.故选B.
9.答案:D
解析:由题意知,AB,CE,FH都垂直于地面AF,,,.,,.m,m, m, m,,(m),(m).故选D.
10.答案:D
解析:如图,过点A作于点M,交于点N,延长交于点H.
,
.
.
,
,
,
.
∵四边形是正方形,
,
.
,
,
,
,
,
,
.
11.答案:(答案不唯一)
解析:,
,
∴当时,,
.
12.答案:
解析:如图,连接,,交点P就是位似中心,则由题意可知平移后点A的坐标是.
13.答案:78
解析:在中,于,点E,
.
又,
故,
.
,
.
14.答案:
解析:,
,
,
,
,解得.
15.答案:1.2
解析:如图,延长交于点M,当时,点P到的距离最小,
,
,
.
,
,
,
,
,
.
∴点P到边距离的最小值是1.2.
16.答案:(1)(0,1)
(2)
解析:(1)如图所示,其中的坐标为(0,1).
(2)符合条件的有两个,如图所示.
17.答案:证明:(1)∵四边形是平行四边形,
且,
,点F是的中点,
(2)四边形为菱形.
理由如下:.
∴四边形为平行四边形.
∴四边形为菱形.
18.答案:20.7
解析:由题意可知.
又为公共角,
.
米,点B是的中点,
米.
米,米,
,
米.
又为公共角,
,
米,米.
答:甲、乙两人的观测点到地面的距离之差约为20.7米.
19.答案:(1)见解析
(2)
解析:(1)证明:∵四边形是平行四边形,
.
.
又.
(2)∵四边形是平行四边形,
,即,
,
,
,
∵四边形是平行四边形,,
,
,
,
,
即.
20.答案:(1)(ⅰ)假.(ⅱ)假.(ⅲ)真.
(2)证明:如图,连接BD,.
,且,
,
,,.
,,
,
,
,
,,,
,,
又,,,
四边形ABCD与四边形相似.
(3)四边形与四边形EFCD相似,
,
,
,
,
,,
,,
,
,
,
,.
21.答案:问题探究(1)
(2)证明见解析
问题拓展
解析:(2)证明:如图(1),取BC的中点H,连接DH.
是AC的中点,,.
,,.
,.
,
,
,.
,,
,即,
,故(1)中结论仍然成立.
另解1:证明,得也可求解.
另解2:取AB的中点M,证明也可以求解.
问题拓展如图(2),过点D作交BC于点M.
(2)设,则,.
点D为AC的中点,,
,
.
同(2)可证,
,
,.
,
,
,
.
一、选择题:(共10小题)
1.在比例尺是1:38 000的黄浦江交通游览图上,某隧道长约7cm,它的实际长度约为( )
A.266 km B.26.6km C.2.66km D.0.266km
2.如图,已知都与垂直,垂足分别是,且,那么的长是( )
A. B. C. D.
3.如图,在中,D、E分别为线段BC、BA的中点,设的面积为,的面积为.则( )
A. B. C. D.
4.如图,在中,,,则的长为
( )
A.6 B.8 C.10 D.12
5.如图所示,一般书本的纸张是由原纸张多次对开得到的,矩形ABCD沿EF对开后,再把矩形EFCD沿MN对开,依次类推,若各种开本的矩形都相似,则等于( )
A.0.618 B. C. D.2
6.如图,和是以点E为位似中心的位似图形,已知点,点,点,则点D的对应点B的坐标是( )
A.(4,2) B.(4,1) C.(5,2) D.(5,1)
7.如图,小明为了测量一凉亭的高度(顶端A到水平地面的距离),在凉亭的旁边放置一个与凉亭台阶等高的台阶米,三点共线),把一面镜子水平放置在平台上的点G处,测得米,然后沿直线后退到点E处,这时恰好在镜子里看到凉亭的顶端A,测得米,小明身高米,则凉亭的高度约为( )
A.8.5米 B.9米 C.9.5米 D.10米
8.如图,D是等边边上的一点,且,现将折叠,使点C与点D重合,折痕为,点分别在和上,则的值为( )
A. B. C. D.
9.如图,在剧场中,坐在小明(AB)前面一排的女士(CD)戴着高帽子(m),此时小明的眼睛B,帽顶E以及舞台上方横梁的某点H在同一条直线上;女士发现帽子挡住了小明的视线,于是摘掉帽子,此时小明的眼睛B,女士头顶D以及舞台下方地面上某点F在同一条直线上.已知舞台的高m,A、C、F在同一条直线上,F、G、H在同一条直线上, m, m,则舞台横梁到舞台的距离GH为( )
A.3.2m B.3 m C.2 m D.2.2 m
10.如图,中,,正方形的顶点在内,顶点分别在上,,则点F到的距离为( )
A.1 B.2 C. D.
二、填空题(共10小题)
11.如图,在中,分别为边上的点,,点F为边上一点,添加一个条件:____________,可以使得与相似.(只需写出一个)
12.如图,在平面直角坐标系中,与的顶点都在格点(网格线的交点)上,且与关于点P位似,若平移平面直角坐标系,使得原点与点P重合,则平移后点A的坐标为_____________.
13.如图,在中,,点D在边上,于点E,连接,则的面积等于________.
14.如图,,点在上,与交于点,,则的长为__________.
15.如图,在中,,点F在边上,且,点E为边上的动点,将沿直线翻折,点C落在点P处,则点P到边距离的最小值是_________.
三、解答题(共6小题)
16.如图,已知是直角坐标系平面上三点.
(1)把向右平移4个单位再向下平移1个单位,得到.画出平移后的图形,并写出点A的对应点的坐标;
(2)以原点O为位似中心,将的周长缩小为原来的一半,得到,请在所给的坐标系中作出所有满足条件的图形.
17.如图,在平行四边形中,F是边的中点,延长,与延长线相交于点E,连接.
(1)求证:;
(2)若平分,请判断并证明四边形的形状.
18.如图,在相对的两栋楼中间有一堵墙,甲、乙两人分别在这两栋楼内观察这堵墙,视线如图1所示.根据实际情况画出平面图形如图2(),甲从点C可以看到点G处,乙从点E可以看到点D处,点B是的中点,墙高5.5米,米,米,求甲、乙两人的观测点到地面的距离之差(结果精确到0.1米).
19.如图,已知四边形是平行四边形,点E在边的延长线上,交于点F,.
(1)求证:;
(2)若,求的值.
20.根据相似多边形的定义,我们把四个角分别相等,四条边成比例的两个凸四边形叫做相似四边形.相似四边形对应边的比叫做相似比.
(1)某同学在探究相似四边形的判定时,得到如下三个命题,请判断它们是否正确(直接在横线上填写“真”或“假”).
(ⅰ)各边成比例的两个凸四边形相似;(_________命题)
(ⅱ)三个角分别相等的两个凸四边形相似;(________命题)
(ⅲ)两个大小不同的正方形相似;(_________命题)
(2)如图①,在四边形ABCD和四边形中,,,.求证:四边形ABCD与四边形相似;
(3)如图②,四边形ABCD中,,AC与BD相交于点O,过点O作分别交AD,BC于点E,F.记四边形ABFE的面积为,四边形EFCD的面积为,若四边形与四边形EFCD相似,求的值.
21.问题提出
如图(1),在中,,D是AC的中点,延长BC至点E,使,延长ED交AB于点F,探究的值.
问题探究
(1)先将问题特殊化.如图(2),当时,直接写出的值;
(2)再探究一般情形.如图(1),证明(1)中的结论仍然成立.
问题拓展
如图(3),在中,,D是AC的中点,G是边BC上一点,(),延长BC至点E,使,延长ED交AB于点F.直接写出的值(用含n的式子表示).
答案以及解析
1.答案:C
解析:设隧道的实际长度是,根据题意得,解得,.
2.答案:C
解析:都与垂直,
,
,
.
同理,
,
,故选C.
3.答案:B
解析:在中,D、E分别为线段BC、BA的中点,DE为的中位线,,,,,,即,故选:B.
4.答案:C
解析:,四边形是平行四边形,,,故选C.
5.答案:C
解析:由题意得,且,,即,.故选C.
6.答案:C
解析:设点B的坐标为.
和是以点E为位似中心的位似图形,
,
解得点B的坐标为(5,2).故选C.
7.答案:A
解析:由题意可知.
又,
,
,
,
米,
(米).
8.答案:B
解析:由折叠可知,
所以.
在中,因为,
所以,
所以.
又因为,
所以,
所以.
设,
则,
则,
取,可得,①
取,可得,②
①+②得,即,
由比例的基本性质可得.故选B.
9.答案:D
解析:由题意知,AB,CE,FH都垂直于地面AF,,,.,,.m,m, m, m,,(m),(m).故选D.
10.答案:D
解析:如图,过点A作于点M,交于点N,延长交于点H.
,
.
.
,
,
,
.
∵四边形是正方形,
,
.
,
,
,
,
,
,
.
11.答案:(答案不唯一)
解析:,
,
∴当时,,
.
12.答案:
解析:如图,连接,,交点P就是位似中心,则由题意可知平移后点A的坐标是.
13.答案:78
解析:在中,于,点E,
.
又,
故,
.
,
.
14.答案:
解析:,
,
,
,
,解得.
15.答案:1.2
解析:如图,延长交于点M,当时,点P到的距离最小,
,
,
.
,
,
,
,
,
.
∴点P到边距离的最小值是1.2.
16.答案:(1)(0,1)
(2)
解析:(1)如图所示,其中的坐标为(0,1).
(2)符合条件的有两个,如图所示.
17.答案:证明:(1)∵四边形是平行四边形,
且,
,点F是的中点,
(2)四边形为菱形.
理由如下:.
∴四边形为平行四边形.
∴四边形为菱形.
18.答案:20.7
解析:由题意可知.
又为公共角,
.
米,点B是的中点,
米.
米,米,
,
米.
又为公共角,
,
米,米.
答:甲、乙两人的观测点到地面的距离之差约为20.7米.
19.答案:(1)见解析
(2)
解析:(1)证明:∵四边形是平行四边形,
.
.
又.
(2)∵四边形是平行四边形,
,即,
,
,
,
∵四边形是平行四边形,,
,
,
,
,
即.
20.答案:(1)(ⅰ)假.(ⅱ)假.(ⅲ)真.
(2)证明:如图,连接BD,.
,且,
,
,,.
,,
,
,
,
,,,
,,
又,,,
四边形ABCD与四边形相似.
(3)四边形与四边形EFCD相似,
,
,
,
,
,,
,,
,
,
,
,.
21.答案:问题探究(1)
(2)证明见解析
问题拓展
解析:(2)证明:如图(1),取BC的中点H,连接DH.
是AC的中点,,.
,,.
,.
,
,
,.
,,
,即,
,故(1)中结论仍然成立.
另解1:证明,得也可求解.
另解2:取AB的中点M,证明也可以求解.
问题拓展如图(2),过点D作交BC于点M.
(2)设,则,.
点D为AC的中点,,
,
.
同(2)可证,
,
,.
,
,
,
.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
