八年级数学上册《11.1.1 三角形的边》 课件(28页PPT)
文档属性
| 名称 | 八年级数学上册《11.1.1 三角形的边》 课件(28页PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-05 10:00:38 | ||
图片预览







文档简介
(共28张PPT)
11.1.1三角形的边
人教版八年级上册
第十一章 三角形
教学目标
1.通过观察、操作、想象、推理、交流等活动,发展空间观念、推理能力和表达能力。
2.通过具体实例,进一步认识三角形的概念及其基本要素。
3.学会三角形的表示及根据“是否有边相等”对三角形进行的分类。
4.掌握三角形三条边之间的关系。
新知导入
三角形是我们早已熟悉的图形,你能列举出
日常生活中形如三角形的物体吗?
对于三角形,你了解了哪些方面的知识?
新知讲解
一、三角形
1.定义:由 的三条线段首尾 所组成的
图形叫做三角形。
2.有关概念
如图,线段AB,BC,CA是三角形的 ,
点A,B,C是三角形的 ,∠A,∠B,
∠C是相邻两边组成的角,叫做三角形
的 ,简称三角形的角。
不在同一条直线上
顺次连接
边
顶点
内角
新知讲解
3.表示方法:顶点是A,B,C的三角形,记作“ ”,
读作“ ”。
△ABC
三角形ABC
新知讲解
教 师 点 拨
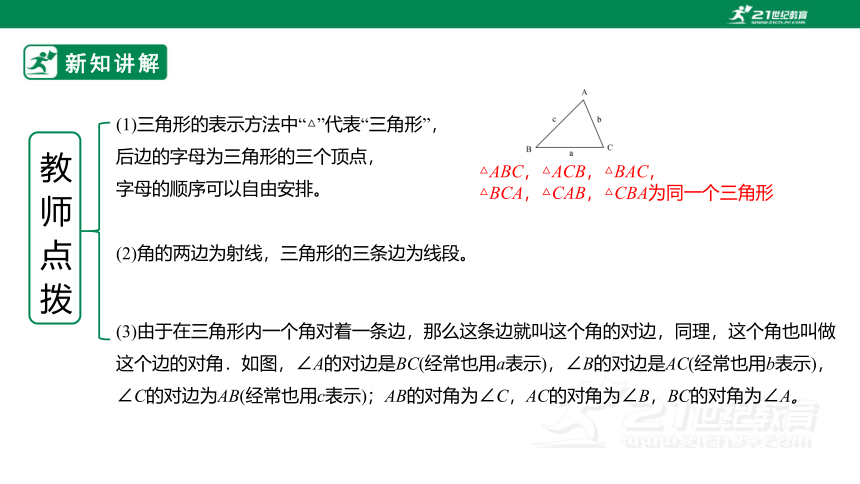
(1)三角形的表示方法中“△”代表“三角形”,
后边的字母为三角形的三个顶点,
字母的顺序可以自由安排。
△ABC,△ACB,△BAC,
△BCA,△CAB,△CBA为同一个三角形
(2)角的两边为射线,三角形的三条边为线段。
(3)由于在三角形内一个角对着一条边,那么这条边就叫这个角的对边,同理,这个角也叫做这个边的对角.如图,∠A的对边是BC(经常也用a表示),∠B的对边是AC(经常也用b表示),∠C的对边为AB(经常也用c表示);AB的对角为∠C,AC的对角为∠B,BC的对角为∠A。
新知讲解
课 堂 小 练 习
1.小强用三根木棒组成下列图形,其中符合三角形概念是( )
2.找一找,图中有多少个三角形,并把它们写下来。
C
解:图中有5个三角形。
分别是:△ABE、△DEC、△BEC、△ABC、△DBC。
新知讲解
二、三角形的分类
1.等边三角形:三条边都 的三角形。
2.等腰三角形:有两边 的三角形,其中相等的两条边叫做 ,另一边叫做 ,两腰的夹角叫做 ,腰和底边的夹角叫做 。
3.不等边三角形:三条边都 的三角形。
相等
相等
腰
底边
顶角
底角
不相等
新知讲解
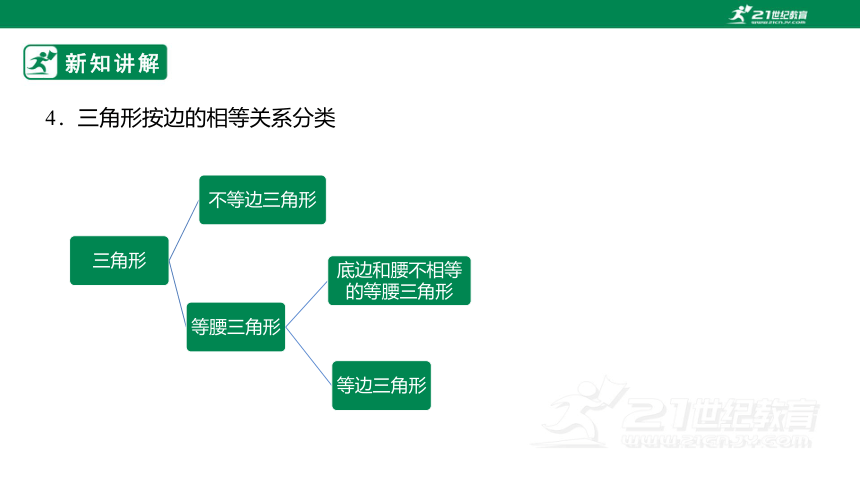
4.三角形按边的相等关系分类
新知讲解
5.三角形的三边关系
对于任意一个△ABC,如果把其中任意两个顶点(如B、C)看成定点,
则由“两点之间,线段最短”可得
AB+BC>BC ①
同理,可得: 、
AB+BC>AC ③
AC+BC>AB ②
一般地,我们有:
三角形两边的和大于第三边
由不等式②③移项,可得 、
由此可得结论:
BC>AC-AB
BC>AB-AC
三角形两边的差小于第三边
新知讲解
教 师 点 拨
(1)组成一个三角形必须满足任意两条线段的和大于另一条线段。
(2)三角形两边之和大于第三边指的是三角形任意两边之和大于第三边,即a+b>c,b+c>a,c+a>b三个不等式同时成立
(3)用较短的两条线段之和与最长的线段比较,若和大,能组成三角形;反之,则不能。
新知讲解
课 堂 小 练 习
1、判断下列长度的三条线段能否组成三角形。
(1)3,4,8 ( )
(2)2,5,6 ( )
(3)5,6,10 ( )
(4)5,6,11 ( )
不能
能
能
不能
新知讲解
课 堂 小 练 习
2、若三角形的两边长分别是2和7,第三边长为奇数,求第三边的长。
解:设第三边的长为x
根据两边之和大于第三边得:x<2+7
即x<9
根据两边之差小于第三边得:x>7-2
即x>5
∴x的值大于5小于9
又∵它是奇数
∴x只能取7
∴第三边的长为7
新知讲解
例题:用一根长为18cm的细铁丝围成一个等腰三角形
(1)如果腰长是底边的2倍,那么各边的长是多少?
(1)解:设底边长为xcm,则腰长为2xcm.则
x+2x+2x=18
解得x=3.6
∴三边长分别为3.6cm,7.2cm,7.2cm。
新知讲解
(2)能围成有一边的长为4cm的等腰三角形吗?
(2)解:①当4cm长为底边,设腰长为xcm
则4+2x=18
解得x=7
∴等腰三角形的三边长为7cm、7cm、4cm。
②当4cm长为腰长,设底边长为xcm,可得
4×2+x=18
解得x=10
∵4+4<10,不符合三角形两边和大于第三边
∴此时不能构成三角形
综上可得,可围成等腰三角形,且三边长分别为7cm、7cm和4cm
课堂练习
1、(2021秋 双牌县期末)下面是小强用三根火柴组成的图形,其中符合三角形概念的是( )
A B C D
【解析】三角形是由不在同一条直线上的三条线段首尾顺次相接所成的图形,故答案选C。
C
课堂练习
2、(2022春 渝中区校级期中)下列三条线段,首尾顺次相连不能围成三角形的是( )
A.2、4、5 B.10、10、10
C.3、3、6 D.7、24、25
【解析】A、4+2>5,故能构成三角形,故此选项不符合题意;
B、10+10>10,故能构成三角形,故此选项不符合题意;
C、3+3=6,不能构成三角形,故此选项符合题意;
D、7+24>25,故能构成三角形,故此选项不符合题意。
C
课堂练习
3、(2021秋 岚皋县校级月考)图中以AE为边的三角形共有 个
【解析】图中以AE为边的三角形有△AEC,△AED,△AEB共3个
4、(2022春 金牛区校级期中)三角形三边为3,5,x,则x的范围是 。
【解析】∵三角形三边为3,5,x
∴5﹣3<x<5+3
∴2<x<8
故答案为:2<x<8
3
2<x<8
课堂练习
5、(2021秋 隆回县期中)已知a,b,c是△ABC的三边,a=4,b=6,若三角形的周长是小于18的偶数。
(1)求c边的长;
(2)判断△ABC的形状。
解:(1)∵a,b,c是△ABC的三边,a=4,b=6
∴2<c<10
∵三角形的周长是小于18的偶数
∴2<c<8
∴c=4或6
(2)当c=4或6时,△ABC的形状都是等腰三角形
课堂总结
作业布置
1、(2021秋 西青区期末)小芳有两根长度为5cm和10cm的木条,她想钉一个三角形木框,桌上有下列长度的几根木条,她应该选择长度为( )的木条.
A.5cm B.3cm C.17cm D.12cm
【解析】设木条的长度为xcm,则10﹣5<x<10+5,即5<x<15;故答案选D。
D
作业布置
2、(2020秋 交城县期中)给出下列说法:(1)等边三角形是等腰三角形;
(2)三角形按边的相等关系分类可分为等腰三角形、等边三角形和不等边三角形;
(3)三角形按角的大小分类可分为锐角三角形、直角三角形和钝角三角形.
其中,正确的有( )个.
A.1 B.2 C.3 D.0
【解析】(1)等边三角形是一特殊的等腰三角形,正确;
(2)三角形按边分类可以分为不等边三角形和等腰三角形,错误;
(3)三角形按角分类应分为锐角三角形、直角三角形和钝角三角形,正确。
综上所述,正确的结论2个,故答案选B。
B
作业布置
3、(2020秋 饶平县校级期末)若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC为公共边的“共边三角形”有 对。
【解析】以BC为公共边的“共边三角形”有:△BDC与△BEC、△BDC与△BAC、△BEC与△BAC三对。
3
4、(2021秋 隆昌市校级期末)△ABC的三边长为a、b、c,且a、b满足
则c的取值范围是 。
【解析】∵
∴a=2,b=4
∴2<c<6
故答案为:2<c<6
2<c<6
作业布置
5、(2021秋 临江市期末)两根木棒分别长3cm、7cm,第三根木棒与这两根木棒首尾依次相接构成三角形。如果第三根木棒的长为偶数(单位:cm),那么所构成的三角形周长为 cm。
【解析】根据三角形的三边关系,得
第三根木棒的长大于4cm而小于10cm
又第三根木棒的长是偶数,则应为6cm,8cm
∴所构成的三角形周长为16cm或18cm
故答案为:16或18
16或18
作业布置
6、(2021秋 富县月考)已知三角形的两边长分别是4和9,第三边长是偶数,求第三边的长。
解:设第三边长为xcm,根据三角形的三边关系定理可得:9﹣4<x<9+4
解得:5<x<13
∵第三边长是偶数
∴x=6,8,10,12
∴第三边的长是6或8或10或12
作业布置
7、(2020秋 东莞市校级期中)一个三角形有两条边相等,周长为20cm,三角形的一边长6cm,求其他两边长。
解:(1)当6是腰时,底边=20﹣6×2=8cm
即其它两边是6cm,8cm
此时6+6=12,能构成三角形
(2)当6是底边时,腰=(20﹣6)÷2=7cm
此时能构成三角形
所以其它两边是7cm、7cm
因此其它两边长分别为7cm,7cm
综上所述两边长分别为6cm,8cm或7cm,7cm
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
11.1.1三角形的边
人教版八年级上册
第十一章 三角形
教学目标
1.通过观察、操作、想象、推理、交流等活动,发展空间观念、推理能力和表达能力。
2.通过具体实例,进一步认识三角形的概念及其基本要素。
3.学会三角形的表示及根据“是否有边相等”对三角形进行的分类。
4.掌握三角形三条边之间的关系。
新知导入
三角形是我们早已熟悉的图形,你能列举出
日常生活中形如三角形的物体吗?
对于三角形,你了解了哪些方面的知识?
新知讲解
一、三角形
1.定义:由 的三条线段首尾 所组成的
图形叫做三角形。
2.有关概念
如图,线段AB,BC,CA是三角形的 ,
点A,B,C是三角形的 ,∠A,∠B,
∠C是相邻两边组成的角,叫做三角形
的 ,简称三角形的角。
不在同一条直线上
顺次连接
边
顶点
内角
新知讲解
3.表示方法:顶点是A,B,C的三角形,记作“ ”,
读作“ ”。
△ABC
三角形ABC
新知讲解
教 师 点 拨
(1)三角形的表示方法中“△”代表“三角形”,
后边的字母为三角形的三个顶点,
字母的顺序可以自由安排。
△ABC,△ACB,△BAC,
△BCA,△CAB,△CBA为同一个三角形
(2)角的两边为射线,三角形的三条边为线段。
(3)由于在三角形内一个角对着一条边,那么这条边就叫这个角的对边,同理,这个角也叫做这个边的对角.如图,∠A的对边是BC(经常也用a表示),∠B的对边是AC(经常也用b表示),∠C的对边为AB(经常也用c表示);AB的对角为∠C,AC的对角为∠B,BC的对角为∠A。
新知讲解
课 堂 小 练 习
1.小强用三根木棒组成下列图形,其中符合三角形概念是( )
2.找一找,图中有多少个三角形,并把它们写下来。
C
解:图中有5个三角形。
分别是:△ABE、△DEC、△BEC、△ABC、△DBC。
新知讲解
二、三角形的分类
1.等边三角形:三条边都 的三角形。
2.等腰三角形:有两边 的三角形,其中相等的两条边叫做 ,另一边叫做 ,两腰的夹角叫做 ,腰和底边的夹角叫做 。
3.不等边三角形:三条边都 的三角形。
相等
相等
腰
底边
顶角
底角
不相等
新知讲解
4.三角形按边的相等关系分类
新知讲解
5.三角形的三边关系
对于任意一个△ABC,如果把其中任意两个顶点(如B、C)看成定点,
则由“两点之间,线段最短”可得
AB+BC>BC ①
同理,可得: 、
AB+BC>AC ③
AC+BC>AB ②
一般地,我们有:
三角形两边的和大于第三边
由不等式②③移项,可得 、
由此可得结论:
BC>AC-AB
BC>AB-AC
三角形两边的差小于第三边
新知讲解
教 师 点 拨
(1)组成一个三角形必须满足任意两条线段的和大于另一条线段。
(2)三角形两边之和大于第三边指的是三角形任意两边之和大于第三边,即a+b>c,b+c>a,c+a>b三个不等式同时成立
(3)用较短的两条线段之和与最长的线段比较,若和大,能组成三角形;反之,则不能。
新知讲解
课 堂 小 练 习
1、判断下列长度的三条线段能否组成三角形。
(1)3,4,8 ( )
(2)2,5,6 ( )
(3)5,6,10 ( )
(4)5,6,11 ( )
不能
能
能
不能
新知讲解
课 堂 小 练 习
2、若三角形的两边长分别是2和7,第三边长为奇数,求第三边的长。
解:设第三边的长为x
根据两边之和大于第三边得:x<2+7
即x<9
根据两边之差小于第三边得:x>7-2
即x>5
∴x的值大于5小于9
又∵它是奇数
∴x只能取7
∴第三边的长为7
新知讲解
例题:用一根长为18cm的细铁丝围成一个等腰三角形
(1)如果腰长是底边的2倍,那么各边的长是多少?
(1)解:设底边长为xcm,则腰长为2xcm.则
x+2x+2x=18
解得x=3.6
∴三边长分别为3.6cm,7.2cm,7.2cm。
新知讲解
(2)能围成有一边的长为4cm的等腰三角形吗?
(2)解:①当4cm长为底边,设腰长为xcm
则4+2x=18
解得x=7
∴等腰三角形的三边长为7cm、7cm、4cm。
②当4cm长为腰长,设底边长为xcm,可得
4×2+x=18
解得x=10
∵4+4<10,不符合三角形两边和大于第三边
∴此时不能构成三角形
综上可得,可围成等腰三角形,且三边长分别为7cm、7cm和4cm
课堂练习
1、(2021秋 双牌县期末)下面是小强用三根火柴组成的图形,其中符合三角形概念的是( )
A B C D
【解析】三角形是由不在同一条直线上的三条线段首尾顺次相接所成的图形,故答案选C。
C
课堂练习
2、(2022春 渝中区校级期中)下列三条线段,首尾顺次相连不能围成三角形的是( )
A.2、4、5 B.10、10、10
C.3、3、6 D.7、24、25
【解析】A、4+2>5,故能构成三角形,故此选项不符合题意;
B、10+10>10,故能构成三角形,故此选项不符合题意;
C、3+3=6,不能构成三角形,故此选项符合题意;
D、7+24>25,故能构成三角形,故此选项不符合题意。
C
课堂练习
3、(2021秋 岚皋县校级月考)图中以AE为边的三角形共有 个
【解析】图中以AE为边的三角形有△AEC,△AED,△AEB共3个
4、(2022春 金牛区校级期中)三角形三边为3,5,x,则x的范围是 。
【解析】∵三角形三边为3,5,x
∴5﹣3<x<5+3
∴2<x<8
故答案为:2<x<8
3
2<x<8
课堂练习
5、(2021秋 隆回县期中)已知a,b,c是△ABC的三边,a=4,b=6,若三角形的周长是小于18的偶数。
(1)求c边的长;
(2)判断△ABC的形状。
解:(1)∵a,b,c是△ABC的三边,a=4,b=6
∴2<c<10
∵三角形的周长是小于18的偶数
∴2<c<8
∴c=4或6
(2)当c=4或6时,△ABC的形状都是等腰三角形
课堂总结
作业布置
1、(2021秋 西青区期末)小芳有两根长度为5cm和10cm的木条,她想钉一个三角形木框,桌上有下列长度的几根木条,她应该选择长度为( )的木条.
A.5cm B.3cm C.17cm D.12cm
【解析】设木条的长度为xcm,则10﹣5<x<10+5,即5<x<15;故答案选D。
D
作业布置
2、(2020秋 交城县期中)给出下列说法:(1)等边三角形是等腰三角形;
(2)三角形按边的相等关系分类可分为等腰三角形、等边三角形和不等边三角形;
(3)三角形按角的大小分类可分为锐角三角形、直角三角形和钝角三角形.
其中,正确的有( )个.
A.1 B.2 C.3 D.0
【解析】(1)等边三角形是一特殊的等腰三角形,正确;
(2)三角形按边分类可以分为不等边三角形和等腰三角形,错误;
(3)三角形按角分类应分为锐角三角形、直角三角形和钝角三角形,正确。
综上所述,正确的结论2个,故答案选B。
B
作业布置
3、(2020秋 饶平县校级期末)若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC为公共边的“共边三角形”有 对。
【解析】以BC为公共边的“共边三角形”有:△BDC与△BEC、△BDC与△BAC、△BEC与△BAC三对。
3
4、(2021秋 隆昌市校级期末)△ABC的三边长为a、b、c,且a、b满足
则c的取值范围是 。
【解析】∵
∴a=2,b=4
∴2<c<6
故答案为:2<c<6
2<c<6
作业布置
5、(2021秋 临江市期末)两根木棒分别长3cm、7cm,第三根木棒与这两根木棒首尾依次相接构成三角形。如果第三根木棒的长为偶数(单位:cm),那么所构成的三角形周长为 cm。
【解析】根据三角形的三边关系,得
第三根木棒的长大于4cm而小于10cm
又第三根木棒的长是偶数,则应为6cm,8cm
∴所构成的三角形周长为16cm或18cm
故答案为:16或18
16或18
作业布置
6、(2021秋 富县月考)已知三角形的两边长分别是4和9,第三边长是偶数,求第三边的长。
解:设第三边长为xcm,根据三角形的三边关系定理可得:9﹣4<x<9+4
解得:5<x<13
∵第三边长是偶数
∴x=6,8,10,12
∴第三边的长是6或8或10或12
作业布置
7、(2020秋 东莞市校级期中)一个三角形有两条边相等,周长为20cm,三角形的一边长6cm,求其他两边长。
解:(1)当6是腰时,底边=20﹣6×2=8cm
即其它两边是6cm,8cm
此时6+6=12,能构成三角形
(2)当6是底边时,腰=(20﹣6)÷2=7cm
此时能构成三角形
所以其它两边是7cm、7cm
因此其它两边长分别为7cm,7cm
综上所述两边长分别为6cm,8cm或7cm,7cm
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
