北师大版数学八年级上册 第四章 单元复习课 课件(共31张PPT)
文档属性
| 名称 | 北师大版数学八年级上册 第四章 单元复习课 课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 409.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-06 07:28:59 | ||
图片预览











文档简介
(共31张PPT)
第四章 一次函数
单元复习课
本章知识梳理
目录
01
课标要求
02
知识导航
课标要求
1.函数:
(1)通过简单实例中的数量关系,了解常量、变量的意义.
(2)结合实例,了解函数的概念和三种表示方法,能举出函数的实例.
(3)能确定简单实际问题中函数自变量的取值范围,并会求其函数值.
(4)能用适当的函数表示法刻画简单实际问题中变量之间的关系.
2.一次函数:
(1)结合具体情境体会一次函数的意义,根据已知条件确定一次函数表达式.
(2)会利用待定系数法确定一次函数的表达式.
(3)能画出一次函数的图象,根据一次函数的图象和表达式y=kx+b(k≠0)探索并理解k>0或k<0时,图象的变化情况.
(4)理解正比例函数.
(5)能用一次函数解决简单实际问题.
知识导航
一次函数 函数 定义:如果在一个变化过程中有两个变量x和y,并且对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们称y是x的函数,其中x 是自变量
表示方法:列表法、关系式法、图象法
自变量的取值范围:使函数关系式有意义,同时满足题目中说明的其他条件
续表
一次函数 一次函数 正比例函数 表达式:y=kx(k≠0)
图象与性质:是一条经过原点的直线,
(1)当k>0,y的值随x值的增大而增大,图象经过第一、三象限;
(2)当k<0,y的值随x值的增大而减小,图象经过第二、四象限
续表
一次函数 一次函数 一次函数 表达式:y=kx+b(k≠0)
图象与性质:是一条经过点(0,b)的直线;
(1)当k>0,y的值随x值的增大而增大;
(2)当k<0,y的值随x值的增大而减小
专题1 一次函数的图象与性质
1.(2020凉山州)若一次函数y=(2m+1)x+m-3的图象不经过第二象限,则m的取值范围是( )
A. m> B. m<3
C. <m<3 D. <m≤3
D
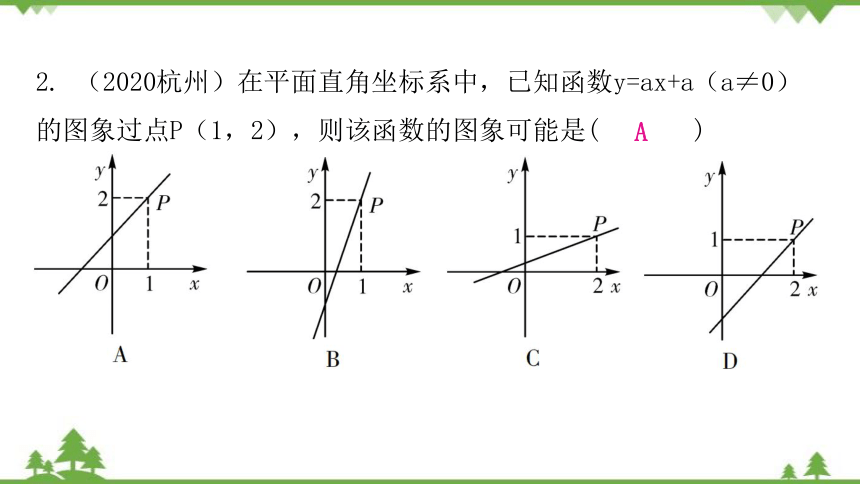
2. (2020杭州)在平面直角坐标系中,已知函数y=ax+a(a≠0)的图象过点P(1,2),则该函数的图象可能是( )
A
3. 一次函数y=2x-3的图象经过的象限是( )
A.第一、二、三象限
B.第二、三、四象限
C.第一、三、四象限
D.第一、二、四象限
C
4. 在平面直角坐标系中,将函数y=3x的图象向上平移6个单位长度,则平移后的图象与x轴的交点坐标为( )
A.(2,0)
B.(-2,0)
C.(6,0)
D.(-6,0)
B
5. 下列关于一次函数y=kx+b(k<0,b>0)的说法,错误的是( )
A.图象经过第一、二、四象限
B.y随x的增大而减小
C.图象与y轴交于点(0,b)
D.当x> 时,y>0
D
6. (2020辽阳)若一次函数y=2x+2的图象经过点(3,m),则m=_________.
7. (1)直线y=5x-2经过第_______________象限;
(2)若直线y=mx+n经过第一、二、三象限,请直接写出m,n的取值范围;
(3)若直线y=mx+n不经过第一象限,请直接写出m,n的取值范围.
8
一、三、四
解:(2)因为直线y=mx+n经过第一、二、三象限,
所以m>0,n>0.
(3)因为直线y=mx+n不经过第一象限,
所以直线y=mx+n经过第二、四象限或第二、三、四象限,
所以m<0,n≤0.
8. 已知一次函数y=2x+4.
(1)在如图Z4-1所示的平面直角坐标系中,画出函数的图象;
(2)求图象与x轴的交点A的坐标和与y轴的交点B的坐标;
(3)在(2)的条件下,求出
△AOB的面积;
(4)利用图象直接写出:当
y<0时,x的取值范围.
解:(1)当x=0时,y=4;当y=0时,x=-2,
则图象如答图Z4-1.
(2)由(1)可知A(-2,0),
B(0,4).
(3)S△AOB= ×2×4=4.
(4)当y<0时,x<-2.
专题2 一次函数的应用
1. (2020北京)有一个装有水的容器,如图Z4-2,容器内的水面高度是10 cm,现向容器内注水,并同时开始计时,在注水过程中,水面高度以每秒0.2 cm的速度匀速增加,则容器注满水之前,容器内的水面高度与对应的注水时间满足的函数关系是( )
A. 正比例函数关系 B. 一次函数关系
C. 二次函数关系 D.反比例函数关系
B
2. 如图Z4-4,OA和BA分别表示甲、乙两名学生运动的一次函数的图象,图中s和t分别表示路程和时间,根据图象判断跑260 m时,快者比慢者少用( )
A.6 s
B.6.5 s
C.7 s
D.7.5 s
D
3. 甲、乙两人沿相同的路线由A地到B地匀速前进,A,B两地间的路程为40 km.他们前进的路程为s(km),甲出发后的时间为t(h),甲、乙前进的路程与时间的函数图象如图Z4-4.根据图象信息,下列说法不正确的是( )
A.甲的速度是10 km/h
B.乙出发0.5 h后与甲相遇
C.乙的速度是40 km/h
D.甲比乙晚到B地2 h
B
4. 一辆轿车离开某城市的距离y(km)与行驶时间t(h)之间的关系式为y=kt+30,其图象如图Z4-5,在1 h到 3 h之间,轿车行驶的路程是_________km.
120
5. 甲、乙两人分别从A,B两地相向而行,他们距B地的距离
s(km)与时间t(h)的关系如图Z4-6,那么乙的速度是________________.
3.6 km/h
6. (2020重庆)周末,自行车骑行爱好者甲、乙两人相约沿同一路线从A地出发前往B地进行骑行训练.甲、乙分别以不同的速度匀速骑行,乙比甲早出发5 min.乙骑行25 min后,甲以原速的
继续骑行,经过一段时间,甲先到达B地,乙一直保持原速
前往B地.在此过程中,甲、乙两人相距的路程y(m)与乙骑行的时间x(min)之间的关系如图Z4-7,则乙比甲晚_________ min到达B地.
12
7. 甲、乙两人进行比赛,甲比乙跑得快,现在甲让乙先跑10 m,甲再起跑.如图Z4-8中l1和l2分别表示甲、乙两人跑步的路程y(m)与甲跑步的时间x(s)之间的函数关系,其中l1的关系式为y1=8x,那么甲追上乙的时候用了_________s.
5
8. (2020青岛)为让更多的学生学会游泳,少年宫新建一个游泳池,其容积为480 m3,该游泳池有甲、乙两个进水口,注水时每个进水口各自的注水速度保持不变.同时打开甲、乙两个进水口注水,游泳池的蓄水量y(m3)与注水时间t(h)之间满足一次函数关系,其图象如图Z4-9.
(1)根据图象求游泳池的蓄水量y(m3)与注水时间t(h)之间的函数关系式,并写出同时打开甲、乙两个进水口的注水速度;
(2)现将游泳池的水全部排空,对池内消毒后再重新注水.已知单独打开甲进水口注满游泳池所用
时间是单独打开乙进水口注满游泳
池所用时间的 倍.求单独打开甲
进水口注满游泳池需多少小时.
解:(1)设y与t的函数解析式为y=kt+b.
由图象,得b=100,①
2k+b=380.②
把①代入②,得k=140.
即y与t的函数关系式是y=140t+100.
同时打开甲、乙两个进水口的注水速度是:(380-100)÷2=140(m3/h).
(2)因为单独打开甲进水口注满游泳池所用时间是单独打开乙进水口注满游泳池所用时间的 倍,
所以甲进水口进水的速度是乙进水口进水速度的 ,
因为同时打开甲、乙两个进水口的注水速度 是140m3/h,
所以甲进水口的进水速度为140÷ 60(m3/h).
480÷60=8(h).
即单独打开甲进水口注满游泳池需8 h.
9. 某儿童游乐场推出甲、乙两种消费卡,设消费次数为x时,所需费用为y元,且y与x的函数关系如图Z4-10.根据图中信息解答下列问题:
(1)分别求出选择这两种卡消费时,
y关于x的函数表达式;
(2)求B点的坐标;
(3)洋洋爸爸准备240元钱用于洋洋
在该游乐场消费,请问选择哪种消费卡更划算?
解:(1)设y甲=k1x.根据题意,得5k1=100.
解得k1=20.所以y甲=20x.
设y乙=k2x+100.根据题意,得
20k2+100=300.解得k2=10.
所以y乙=10x+100.
(2)由图象知,点B满足y=20x=10x+100.
解得x=10,y=200.
所以点B的坐标为(10,200).
(3)甲:20x=240,解得x=12,即甲种消费卡可玩12次;
乙:10x+100=240,解得x=14,即乙种消费卡可玩14次.
因为14>12,所以洋洋爸爸准备240元钱用于洋洋在该游乐场消费,选择乙种消费卡更划算.
谢 谢
第四章 一次函数
单元复习课
本章知识梳理
目录
01
课标要求
02
知识导航
课标要求
1.函数:
(1)通过简单实例中的数量关系,了解常量、变量的意义.
(2)结合实例,了解函数的概念和三种表示方法,能举出函数的实例.
(3)能确定简单实际问题中函数自变量的取值范围,并会求其函数值.
(4)能用适当的函数表示法刻画简单实际问题中变量之间的关系.
2.一次函数:
(1)结合具体情境体会一次函数的意义,根据已知条件确定一次函数表达式.
(2)会利用待定系数法确定一次函数的表达式.
(3)能画出一次函数的图象,根据一次函数的图象和表达式y=kx+b(k≠0)探索并理解k>0或k<0时,图象的变化情况.
(4)理解正比例函数.
(5)能用一次函数解决简单实际问题.
知识导航
一次函数 函数 定义:如果在一个变化过程中有两个变量x和y,并且对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们称y是x的函数,其中x 是自变量
表示方法:列表法、关系式法、图象法
自变量的取值范围:使函数关系式有意义,同时满足题目中说明的其他条件
续表
一次函数 一次函数 正比例函数 表达式:y=kx(k≠0)
图象与性质:是一条经过原点的直线,
(1)当k>0,y的值随x值的增大而增大,图象经过第一、三象限;
(2)当k<0,y的值随x值的增大而减小,图象经过第二、四象限
续表
一次函数 一次函数 一次函数 表达式:y=kx+b(k≠0)
图象与性质:是一条经过点(0,b)的直线;
(1)当k>0,y的值随x值的增大而增大;
(2)当k<0,y的值随x值的增大而减小
专题1 一次函数的图象与性质
1.(2020凉山州)若一次函数y=(2m+1)x+m-3的图象不经过第二象限,则m的取值范围是( )
A. m> B. m<3
C. <m<3 D. <m≤3
D
2. (2020杭州)在平面直角坐标系中,已知函数y=ax+a(a≠0)的图象过点P(1,2),则该函数的图象可能是( )
A
3. 一次函数y=2x-3的图象经过的象限是( )
A.第一、二、三象限
B.第二、三、四象限
C.第一、三、四象限
D.第一、二、四象限
C
4. 在平面直角坐标系中,将函数y=3x的图象向上平移6个单位长度,则平移后的图象与x轴的交点坐标为( )
A.(2,0)
B.(-2,0)
C.(6,0)
D.(-6,0)
B
5. 下列关于一次函数y=kx+b(k<0,b>0)的说法,错误的是( )
A.图象经过第一、二、四象限
B.y随x的增大而减小
C.图象与y轴交于点(0,b)
D.当x> 时,y>0
D
6. (2020辽阳)若一次函数y=2x+2的图象经过点(3,m),则m=_________.
7. (1)直线y=5x-2经过第_______________象限;
(2)若直线y=mx+n经过第一、二、三象限,请直接写出m,n的取值范围;
(3)若直线y=mx+n不经过第一象限,请直接写出m,n的取值范围.
8
一、三、四
解:(2)因为直线y=mx+n经过第一、二、三象限,
所以m>0,n>0.
(3)因为直线y=mx+n不经过第一象限,
所以直线y=mx+n经过第二、四象限或第二、三、四象限,
所以m<0,n≤0.
8. 已知一次函数y=2x+4.
(1)在如图Z4-1所示的平面直角坐标系中,画出函数的图象;
(2)求图象与x轴的交点A的坐标和与y轴的交点B的坐标;
(3)在(2)的条件下,求出
△AOB的面积;
(4)利用图象直接写出:当
y<0时,x的取值范围.
解:(1)当x=0时,y=4;当y=0时,x=-2,
则图象如答图Z4-1.
(2)由(1)可知A(-2,0),
B(0,4).
(3)S△AOB= ×2×4=4.
(4)当y<0时,x<-2.
专题2 一次函数的应用
1. (2020北京)有一个装有水的容器,如图Z4-2,容器内的水面高度是10 cm,现向容器内注水,并同时开始计时,在注水过程中,水面高度以每秒0.2 cm的速度匀速增加,则容器注满水之前,容器内的水面高度与对应的注水时间满足的函数关系是( )
A. 正比例函数关系 B. 一次函数关系
C. 二次函数关系 D.反比例函数关系
B
2. 如图Z4-4,OA和BA分别表示甲、乙两名学生运动的一次函数的图象,图中s和t分别表示路程和时间,根据图象判断跑260 m时,快者比慢者少用( )
A.6 s
B.6.5 s
C.7 s
D.7.5 s
D
3. 甲、乙两人沿相同的路线由A地到B地匀速前进,A,B两地间的路程为40 km.他们前进的路程为s(km),甲出发后的时间为t(h),甲、乙前进的路程与时间的函数图象如图Z4-4.根据图象信息,下列说法不正确的是( )
A.甲的速度是10 km/h
B.乙出发0.5 h后与甲相遇
C.乙的速度是40 km/h
D.甲比乙晚到B地2 h
B
4. 一辆轿车离开某城市的距离y(km)与行驶时间t(h)之间的关系式为y=kt+30,其图象如图Z4-5,在1 h到 3 h之间,轿车行驶的路程是_________km.
120
5. 甲、乙两人分别从A,B两地相向而行,他们距B地的距离
s(km)与时间t(h)的关系如图Z4-6,那么乙的速度是________________.
3.6 km/h
6. (2020重庆)周末,自行车骑行爱好者甲、乙两人相约沿同一路线从A地出发前往B地进行骑行训练.甲、乙分别以不同的速度匀速骑行,乙比甲早出发5 min.乙骑行25 min后,甲以原速的
继续骑行,经过一段时间,甲先到达B地,乙一直保持原速
前往B地.在此过程中,甲、乙两人相距的路程y(m)与乙骑行的时间x(min)之间的关系如图Z4-7,则乙比甲晚_________ min到达B地.
12
7. 甲、乙两人进行比赛,甲比乙跑得快,现在甲让乙先跑10 m,甲再起跑.如图Z4-8中l1和l2分别表示甲、乙两人跑步的路程y(m)与甲跑步的时间x(s)之间的函数关系,其中l1的关系式为y1=8x,那么甲追上乙的时候用了_________s.
5
8. (2020青岛)为让更多的学生学会游泳,少年宫新建一个游泳池,其容积为480 m3,该游泳池有甲、乙两个进水口,注水时每个进水口各自的注水速度保持不变.同时打开甲、乙两个进水口注水,游泳池的蓄水量y(m3)与注水时间t(h)之间满足一次函数关系,其图象如图Z4-9.
(1)根据图象求游泳池的蓄水量y(m3)与注水时间t(h)之间的函数关系式,并写出同时打开甲、乙两个进水口的注水速度;
(2)现将游泳池的水全部排空,对池内消毒后再重新注水.已知单独打开甲进水口注满游泳池所用
时间是单独打开乙进水口注满游泳
池所用时间的 倍.求单独打开甲
进水口注满游泳池需多少小时.
解:(1)设y与t的函数解析式为y=kt+b.
由图象,得b=100,①
2k+b=380.②
把①代入②,得k=140.
即y与t的函数关系式是y=140t+100.
同时打开甲、乙两个进水口的注水速度是:(380-100)÷2=140(m3/h).
(2)因为单独打开甲进水口注满游泳池所用时间是单独打开乙进水口注满游泳池所用时间的 倍,
所以甲进水口进水的速度是乙进水口进水速度的 ,
因为同时打开甲、乙两个进水口的注水速度 是140m3/h,
所以甲进水口的进水速度为140÷ 60(m3/h).
480÷60=8(h).
即单独打开甲进水口注满游泳池需8 h.
9. 某儿童游乐场推出甲、乙两种消费卡,设消费次数为x时,所需费用为y元,且y与x的函数关系如图Z4-10.根据图中信息解答下列问题:
(1)分别求出选择这两种卡消费时,
y关于x的函数表达式;
(2)求B点的坐标;
(3)洋洋爸爸准备240元钱用于洋洋
在该游乐场消费,请问选择哪种消费卡更划算?
解:(1)设y甲=k1x.根据题意,得5k1=100.
解得k1=20.所以y甲=20x.
设y乙=k2x+100.根据题意,得
20k2+100=300.解得k2=10.
所以y乙=10x+100.
(2)由图象知,点B满足y=20x=10x+100.
解得x=10,y=200.
所以点B的坐标为(10,200).
(3)甲:20x=240,解得x=12,即甲种消费卡可玩12次;
乙:10x+100=240,解得x=14,即乙种消费卡可玩14次.
因为14>12,所以洋洋爸爸准备240元钱用于洋洋在该游乐场消费,选择乙种消费卡更划算.
谢 谢
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
