12.2 三角形全等的判定(SSS)课件(共24张PPT)
文档属性
| 名称 | 12.2 三角形全等的判定(SSS)课件(共24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-06 00:00:00 | ||
图片预览




文档简介
(共24张PPT)
12.2三角形全等的判定(SSS)
人教版八年级上册
知识回顾
A
B
C
D
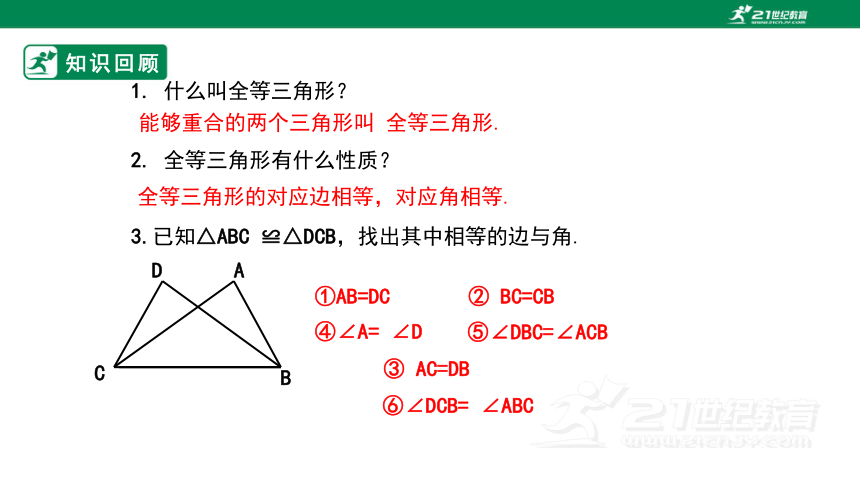
1. 什么叫全等三角形?
能够重合的两个三角形叫 全等三角形.
3.已知△ABC ≌△DCB,找出其中相等的边与角.
①AB=DC
③ AC=DB
② BC=CB
④∠A= ∠D
⑤∠DBC=∠ACB
⑥∠DCB= ∠ABC
2. 全等三角形有什么性质?
全等三角形的对应边相等,对应角相等.
教学目标
1.理解并掌握三角形全等判定“边边边”条件的内容.
2.熟练利用“边边边”条件证明两个三角形全等.
3.通过探究判定三角形全等条件的过程,提高分析和解决问题的能力.
新知导入
当我们在享受科技为我们带来的便利、快捷的生活时,难免遇到出现故障的时候,更换的新零部件要与旧零部件 ,但很多时候我们无法将通过重叠来辨别它们是否全等,本节我们就通过全等三角形来探究三角形全等的条件。
全等
新知导入
A
B
C
D
E
F
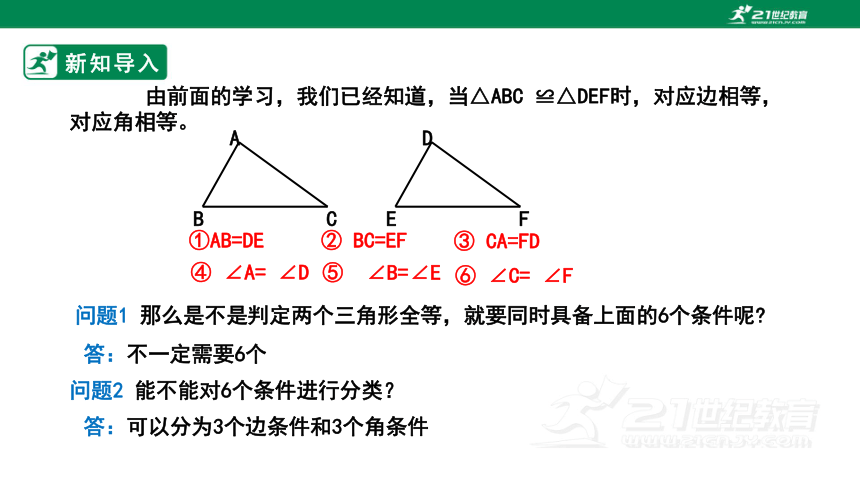
由前面的学习,我们已经知道,当△ABC ≌△DEF时,对应边相等,对应角相等。
①AB=DE
③ CA=FD
② BC=EF
④ ∠A= ∠D
⑤ ∠B=∠E
⑥ ∠C= ∠F
问题1 那么是不是判定两个三角形全等,就要同时具备上面的6个条件呢
问题2 能不能对6个条件进行分类?
答:不一定需要6个
答:可以分为3个边条件和3个角条件
新知探究
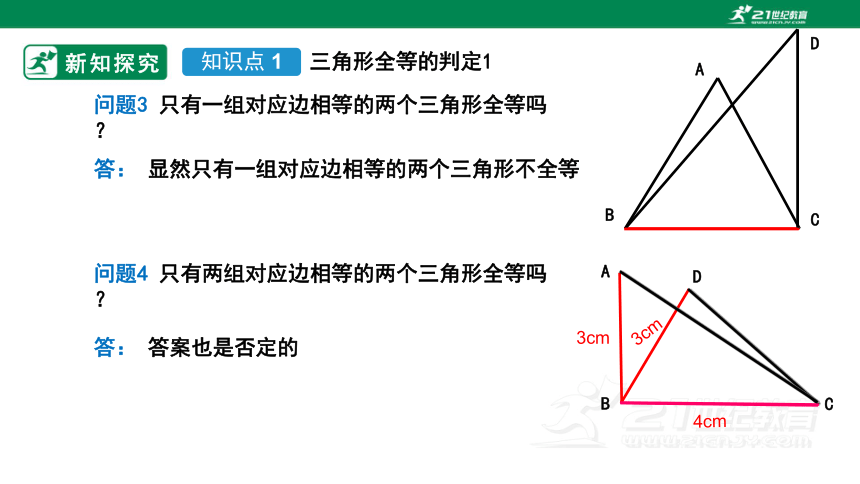
问题3 只有一组对应边相等的两个三角形全等吗?
答: 显然只有一组对应边相等的两个三角形不全等
A
B
C
D
问题4 只有两组对应边相等的两个三角形全等吗?
答: 答案也是否定的
3cm
4cm
3cm
A
B
C
D
知识点 1
三角形全等的判定1
新知探究
问题5: 有3组对应边相等的三角形全等吗?
注意:此时如果直接用2个全等的三角形作为成立的依据,说服力有些不足。我们应该按照已知三角形的三边长,再画一个三边一样长的三角形进行比较,更有说服力。
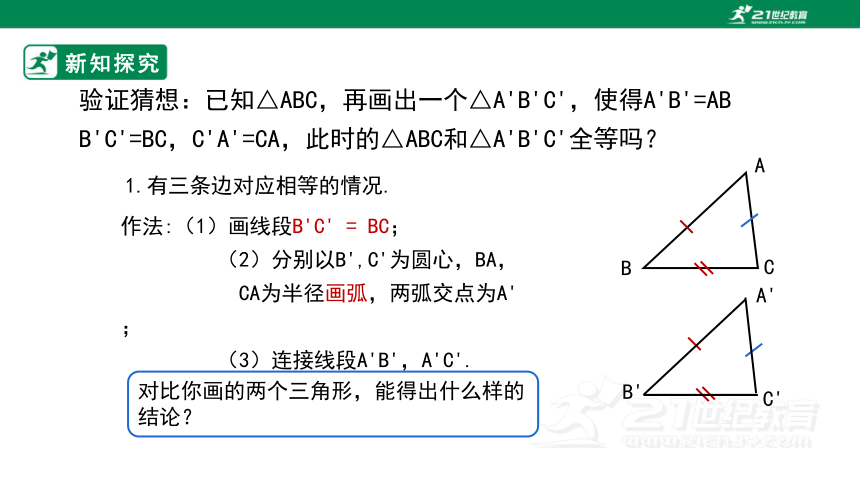
验证猜想:已知△ABC,再画出一个△A'B'C',使得A'B'=AB
B'C'=BC,C'A'=CA,此时的△ABC和△A'B'C'全等吗?
B
C
A
新知探究
作法:(1)画线段B'C' = BC;
(2)分别以B',C'为圆心,BA,
CA为半径画弧,两弧交点为A';
(3)连接线段A'B',A'C'.
1.有三条边对应相等的情况.
对比你画的两个三角形,能得出什么样的结论?
B
C
A
B'
C'
A'
验证猜想:已知△ABC,再画出一个△A'B'C',使得A'B'=AB
B'C'=BC,C'A'=CA,此时的△ABC和△A'B'C'全等吗?
新知探究
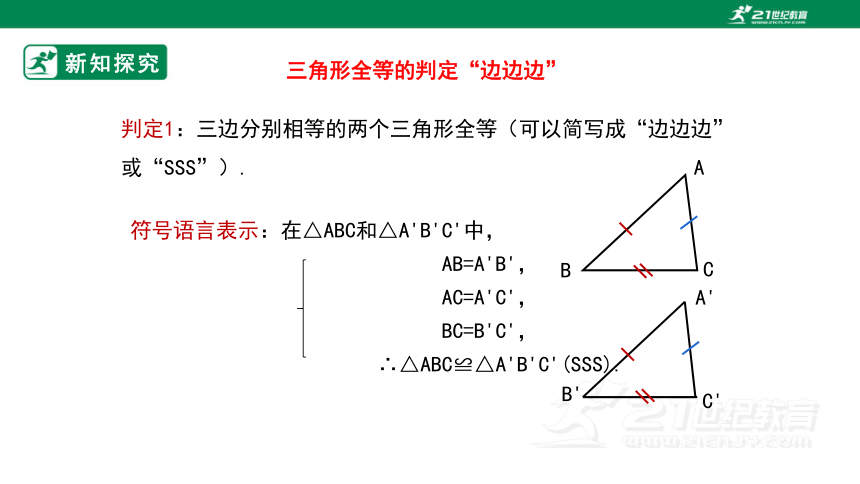
判定1:三边分别相等的两个三角形全等(可以简写成“边边边”或“SSS”).
符号语言表示:在△ABC和△A'B'C'中,
AB=A'B',
AC=A'C',
BC=B'C',
∴△ABC≌△A'B'C'(SSS).
B
C
A
B'
C'
A'
三角形全等的判定“边边边”
A
B
C
D
新知典例
例1 在如图所示的三角形钢架中,AB=AC,AD是连接点A与BC中点D的支架.求证△ABD≌△ACD.
证明:∵点D是BC的中点,∴BD=CD.
在△ABD和△ACD中,
AB=AC,
BD=CD,
AD=AD,
∴ △ABD≌△ACD (SSS).
AD称为公共边.
小结:注意题目和图形中的隐含条件,例如:公共边
新知探究
A
B
C
D
分析、归纳证明步骤
证明:∵点D是BC的中点,∴BD=CD.
在△ABD和△ACD中,
AB=AC,
BD=CD,
AD=AD,
∴ △ABD≌△ACD (SSS).
①准备条件:证全等时要用的条件要先证好;
②指明范围:写出在哪两个三角形中;
③摆齐根据:摆出三个条件用大括号括起来;
④写出结论:写出全等结论.
课堂练习
1. 如图,点C是AB的中点,AD=CE,CD=BE.
求证:△ACD≌△CBE.
证明:∵点C是AB的中点,∴AC=CB.
在△ACD和△CBE中,
AD=CE,
CD=BE,
AC=CB,
∴△ACD≌△CBE(SSS).
D
A
B
C
E
新知探究
用尺规作一个角等于已知角
知识点 2
刚才我们从“边”的角度,通过尺规作图,探究了三角形全等的条件,为了以后能够从“角”的角度探究三角形全等的条件,接下来我们学习如何用尺规作图的方法画一个角等于已知角。
用直尺和圆规作出一个角等于已知角.
如图,已知:∠AOB.
求作:∠A'O'B',使得∠AOB=∠A'O'B'.
A
O
B
新知探究
作法:
(1)以点O 为圆心,任意长为半径画弧,分别交OA,
OB 于点C、D;
(2)画一条射线O′A′,以点O′为圆心,OC 长为半
径画弧,交O′A′于点C′;
(3)以点C′为圆心,CD 长为半径画弧,与第(2)步中
所画的弧交于点D′;
(4)过点D′画射线O′B′,则∠A′O′B′=∠AOB.
如图,已知:∠AOB.
求作:∠A'O'B',使得∠AOB=∠A'O'B'.
O
D
B
C
A
C′
O′
A′
B′
D ′
问题6 为什么按照上述步骤画图后∠A′O′B′=∠AOB呢?
OC=OC′
CD=C′D′
OD=OC
OD=OC′
OD′=OC′
OD=OD′
△COD=△C′O′D′
新知典例
例2 如图,EF=BC,DF=AC,DA=EB.求证:∠F=∠C.
证明:∵DA=BE,∴DE=AB,
在△ABC和△DEF中,
AC=DF(已知)
BC=EF(已知)
∴△ABC≌△DEF(SSS),
∴∠C=∠F.
AB=DE(已证)
课堂练习
证明:∵AD=FB,
∴AD+DB=FB+BD,即AB=FD.
在△ABC和△FDE中,
AC=FE,
BC=DE,
AB=FD,
∴△ABC≌△FDE(SSS),
则∠A=∠F,∠ABC=∠FDE.
∴AC//EF,DE//BC.
3.已知:如图,AC=FE,AD=FB,BC=DE.
求证:AC//EF,DE//BC.
A
C
B
D
E
F
课堂总结
三角形全等的判定
分类
探讨
SSS
尺规
作图
应用
只满足一个条件或者两个条件时不能判定三角形全等
三边分别相等的两个三角形全等
作一个角等于已知角
利用“SSS”解决实际问题
课堂练习
1.如图所示,点A,D,C,F在同一条直线上,AB=DE,AD=CF,要使△ABC≌△DEF,依据“SSS”还需要添加一个条件是( )
A.AD=CD B.BC=EF
C.BC∥EF D.DC=CF
B
2.如图,AB=AC,DB=DC则直接由“SSS”可以判定( )
A.△ABD≌△ACD B.△ABE≌△ACE
C.△EBD≌△ECD D.以上答案都不对
A
课堂练习
3.工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图,在∠AOB的两边OA、OB上分别在取OC=OD,移动角尺,使角尺两边相同的刻度分别与点C、D重合,这时过角尺顶点M的射线OM就是∠AOB的平分线.利用所学知识可知他构造全等三角形的依据是 .
解:在△COM和△DOM中,
∴△COM≌△DOM(SSS),
∴∠COM=∠DOM,
即OM是∠AOB的平分线,
SSS
课堂练习
4.如图,点B、D、C、F在同一条直线上,AB=EF,BD=CF,请添加一个条件(不得添加辅助线),使得△ABC≌△EFD,并说明理由.
解:添加:AC=DE,
∵BD=CF,
∴BD+DC=DC+CF,
即BC=FD,
在△ABC和△EFD中,
∴△ABC≌△EFD(SSS).
AB=EF
BC=DF
AC=DE
课堂练习
5.如图,线段AD,CE相交于点B,BC=BD,AB=EB,AC=DE
求证:△ACD≌△EDC.
证明:∵BC=BD,AB=EB
∴BC+EB=BD+AB
∴AD=EC
即CE=DA
在△ACD与△EDC中
∴△ACD≌△EDC(SSS)
AD=CE
CE=AD
AC=DE
作业布置
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
12.2三角形全等的判定(SSS)
人教版八年级上册
知识回顾
A
B
C
D
1. 什么叫全等三角形?
能够重合的两个三角形叫 全等三角形.
3.已知△ABC ≌△DCB,找出其中相等的边与角.
①AB=DC
③ AC=DB
② BC=CB
④∠A= ∠D
⑤∠DBC=∠ACB
⑥∠DCB= ∠ABC
2. 全等三角形有什么性质?
全等三角形的对应边相等,对应角相等.
教学目标
1.理解并掌握三角形全等判定“边边边”条件的内容.
2.熟练利用“边边边”条件证明两个三角形全等.
3.通过探究判定三角形全等条件的过程,提高分析和解决问题的能力.
新知导入
当我们在享受科技为我们带来的便利、快捷的生活时,难免遇到出现故障的时候,更换的新零部件要与旧零部件 ,但很多时候我们无法将通过重叠来辨别它们是否全等,本节我们就通过全等三角形来探究三角形全等的条件。
全等
新知导入
A
B
C
D
E
F
由前面的学习,我们已经知道,当△ABC ≌△DEF时,对应边相等,对应角相等。
①AB=DE
③ CA=FD
② BC=EF
④ ∠A= ∠D
⑤ ∠B=∠E
⑥ ∠C= ∠F
问题1 那么是不是判定两个三角形全等,就要同时具备上面的6个条件呢
问题2 能不能对6个条件进行分类?
答:不一定需要6个
答:可以分为3个边条件和3个角条件
新知探究
问题3 只有一组对应边相等的两个三角形全等吗?
答: 显然只有一组对应边相等的两个三角形不全等
A
B
C
D
问题4 只有两组对应边相等的两个三角形全等吗?
答: 答案也是否定的
3cm
4cm
3cm
A
B
C
D
知识点 1
三角形全等的判定1
新知探究
问题5: 有3组对应边相等的三角形全等吗?
注意:此时如果直接用2个全等的三角形作为成立的依据,说服力有些不足。我们应该按照已知三角形的三边长,再画一个三边一样长的三角形进行比较,更有说服力。
验证猜想:已知△ABC,再画出一个△A'B'C',使得A'B'=AB
B'C'=BC,C'A'=CA,此时的△ABC和△A'B'C'全等吗?
B
C
A
新知探究
作法:(1)画线段B'C' = BC;
(2)分别以B',C'为圆心,BA,
CA为半径画弧,两弧交点为A';
(3)连接线段A'B',A'C'.
1.有三条边对应相等的情况.
对比你画的两个三角形,能得出什么样的结论?
B
C
A
B'
C'
A'
验证猜想:已知△ABC,再画出一个△A'B'C',使得A'B'=AB
B'C'=BC,C'A'=CA,此时的△ABC和△A'B'C'全等吗?
新知探究
判定1:三边分别相等的两个三角形全等(可以简写成“边边边”或“SSS”).
符号语言表示:在△ABC和△A'B'C'中,
AB=A'B',
AC=A'C',
BC=B'C',
∴△ABC≌△A'B'C'(SSS).
B
C
A
B'
C'
A'
三角形全等的判定“边边边”
A
B
C
D
新知典例
例1 在如图所示的三角形钢架中,AB=AC,AD是连接点A与BC中点D的支架.求证△ABD≌△ACD.
证明:∵点D是BC的中点,∴BD=CD.
在△ABD和△ACD中,
AB=AC,
BD=CD,
AD=AD,
∴ △ABD≌△ACD (SSS).
AD称为公共边.
小结:注意题目和图形中的隐含条件,例如:公共边
新知探究
A
B
C
D
分析、归纳证明步骤
证明:∵点D是BC的中点,∴BD=CD.
在△ABD和△ACD中,
AB=AC,
BD=CD,
AD=AD,
∴ △ABD≌△ACD (SSS).
①准备条件:证全等时要用的条件要先证好;
②指明范围:写出在哪两个三角形中;
③摆齐根据:摆出三个条件用大括号括起来;
④写出结论:写出全等结论.
课堂练习
1. 如图,点C是AB的中点,AD=CE,CD=BE.
求证:△ACD≌△CBE.
证明:∵点C是AB的中点,∴AC=CB.
在△ACD和△CBE中,
AD=CE,
CD=BE,
AC=CB,
∴△ACD≌△CBE(SSS).
D
A
B
C
E
新知探究
用尺规作一个角等于已知角
知识点 2
刚才我们从“边”的角度,通过尺规作图,探究了三角形全等的条件,为了以后能够从“角”的角度探究三角形全等的条件,接下来我们学习如何用尺规作图的方法画一个角等于已知角。
用直尺和圆规作出一个角等于已知角.
如图,已知:∠AOB.
求作:∠A'O'B',使得∠AOB=∠A'O'B'.
A
O
B
新知探究
作法:
(1)以点O 为圆心,任意长为半径画弧,分别交OA,
OB 于点C、D;
(2)画一条射线O′A′,以点O′为圆心,OC 长为半
径画弧,交O′A′于点C′;
(3)以点C′为圆心,CD 长为半径画弧,与第(2)步中
所画的弧交于点D′;
(4)过点D′画射线O′B′,则∠A′O′B′=∠AOB.
如图,已知:∠AOB.
求作:∠A'O'B',使得∠AOB=∠A'O'B'.
O
D
B
C
A
C′
O′
A′
B′
D ′
问题6 为什么按照上述步骤画图后∠A′O′B′=∠AOB呢?
OC=OC′
CD=C′D′
OD=OC
OD=OC′
OD′=OC′
OD=OD′
△COD=△C′O′D′
新知典例
例2 如图,EF=BC,DF=AC,DA=EB.求证:∠F=∠C.
证明:∵DA=BE,∴DE=AB,
在△ABC和△DEF中,
AC=DF(已知)
BC=EF(已知)
∴△ABC≌△DEF(SSS),
∴∠C=∠F.
AB=DE(已证)
课堂练习
证明:∵AD=FB,
∴AD+DB=FB+BD,即AB=FD.
在△ABC和△FDE中,
AC=FE,
BC=DE,
AB=FD,
∴△ABC≌△FDE(SSS),
则∠A=∠F,∠ABC=∠FDE.
∴AC//EF,DE//BC.
3.已知:如图,AC=FE,AD=FB,BC=DE.
求证:AC//EF,DE//BC.
A
C
B
D
E
F
课堂总结
三角形全等的判定
分类
探讨
SSS
尺规
作图
应用
只满足一个条件或者两个条件时不能判定三角形全等
三边分别相等的两个三角形全等
作一个角等于已知角
利用“SSS”解决实际问题
课堂练习
1.如图所示,点A,D,C,F在同一条直线上,AB=DE,AD=CF,要使△ABC≌△DEF,依据“SSS”还需要添加一个条件是( )
A.AD=CD B.BC=EF
C.BC∥EF D.DC=CF
B
2.如图,AB=AC,DB=DC则直接由“SSS”可以判定( )
A.△ABD≌△ACD B.△ABE≌△ACE
C.△EBD≌△ECD D.以上答案都不对
A
课堂练习
3.工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图,在∠AOB的两边OA、OB上分别在取OC=OD,移动角尺,使角尺两边相同的刻度分别与点C、D重合,这时过角尺顶点M的射线OM就是∠AOB的平分线.利用所学知识可知他构造全等三角形的依据是 .
解:在△COM和△DOM中,
∴△COM≌△DOM(SSS),
∴∠COM=∠DOM,
即OM是∠AOB的平分线,
SSS
课堂练习
4.如图,点B、D、C、F在同一条直线上,AB=EF,BD=CF,请添加一个条件(不得添加辅助线),使得△ABC≌△EFD,并说明理由.
解:添加:AC=DE,
∵BD=CF,
∴BD+DC=DC+CF,
即BC=FD,
在△ABC和△EFD中,
∴△ABC≌△EFD(SSS).
AB=EF
BC=DF
AC=DE
课堂练习
5.如图,线段AD,CE相交于点B,BC=BD,AB=EB,AC=DE
求证:△ACD≌△EDC.
证明:∵BC=BD,AB=EB
∴BC+EB=BD+AB
∴AD=EC
即CE=DA
在△ACD与△EDC中
∴△ACD≌△EDC(SSS)
AD=CE
CE=AD
AC=DE
作业布置
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
