数学人教A版2019选择性必修第一册3.1.2 椭圆的简单几何性质(共37张ppt)
文档属性
| 名称 | 数学人教A版2019选择性必修第一册3.1.2 椭圆的简单几何性质(共37张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 100.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-06 16:38:25 | ||
图片预览








文档简介
(共37张PPT)
3.1.2椭圆的简单几何性质
Conic Section
第三章 圆锥曲线的方程
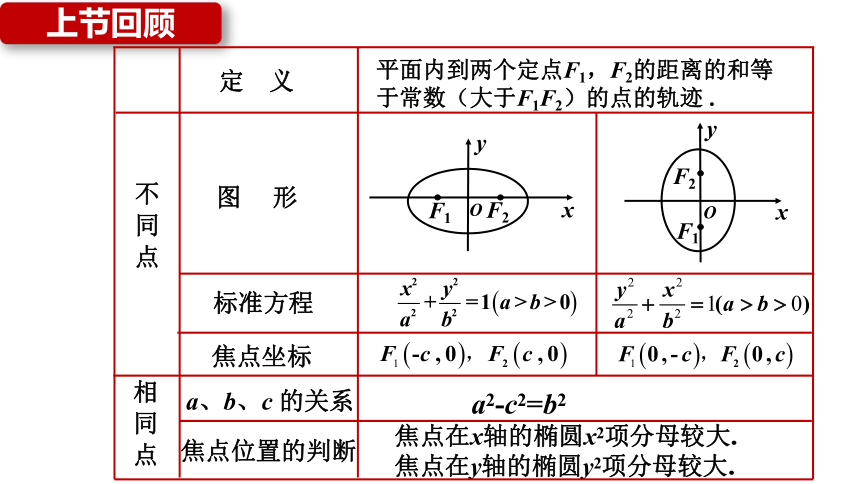
上节回顾
焦点在x轴的椭圆x2项分母较大.
焦点在y轴的椭圆y2项分母较大.
平面内到两个定点F1,F2的距离的和等
于常数(大于F1F2)的点的轨迹 .
标准方程
相 同 点
焦点位置的判断
不 同 点
图 形
焦点坐标
定 义
a、b、c 的关系
a2-c2=b2
x
y
F1
F2
O
x
y
F1
F2
O
C
I
N
O
C
曲线的简单几何性
通过对曲线的范围、对称性及特殊点的讨论,可以从整体上把握曲线的形状、大小和位置。所以,本章对几种圆锥曲线都是从范围、对称性、顶点及其他特性等方面研究它们的几何性质。
目录
CONTENTS
1
2
3
4
探究椭圆的几何性质
椭圆的几何性质的应用
课堂练习
课后小结与预习
壹
第一部分
探究椭圆的几何性质
与利用直线的方程、圆的方程研究它们的几何性质一样,我们利用椭圆的标准方程研究椭圆的几何性质,包括椭圆的范围、形状、大小、对称性和特殊点等.
下面,我们用椭圆方程 来研究椭圆的几何性质.
1.范围
1. 范围
F1
F2
O
x
y
A1
A2
B1
B2
观察图3.1-7,容易看出椭圆上的点都在一个特定的矩形内,为确定其具体的边界,我们利用方程(代数方法)进行研究.
图3.1-7
对称性
由图可知,椭圆是轴对称图形,也是中心对称图形.
所以,坐标轴是椭圆的对称轴,原点是椭圆的对称中心,椭圆的对称中心(即原点)叫做椭圆的中心.
F1
F2
O
x
y
A1(x,y)
A2(x,-y)
A3(-x,y)
A4(-x,-y)
顶点
F1
F2
O
x
y
A1
说明椭圆与y轴有两个交点, 坐标分别为
A1(-a,0),
A2(a,0).
B1(0,-b),
B2(0,b).
说明椭圆与x轴有两个交点, 坐标分别为
所以椭圆与它的对称轴有四个交点, 这四个交点叫做椭圆的顶点(图3.1-8).
线段A1A2, B1B2分别叫做椭圆的长轴和短轴,它们的长分别等于2a, 2b. a和b分别叫做椭圆的长半轴长和短半轴长.
A2
B1
B2
图3.1-8
2a
2b
你认为椭圆上哪些点比较特殊 为什么 如何得到这些点的坐标
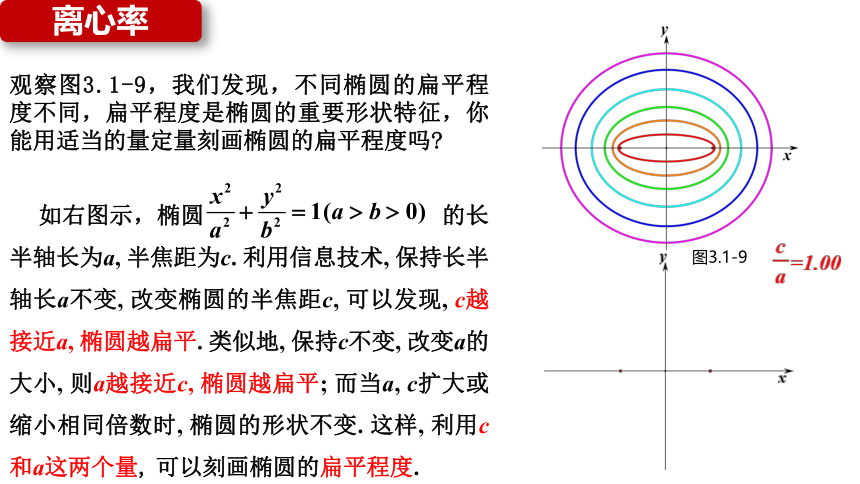
离心率
观察图3.1-9,我们发现,不同椭圆的扁平程度不同,扁平程度是椭圆的重要形状特征,你能用适当的量定量刻画椭圆的扁平程度吗
图3.1-9
如右图示,椭圆 的长半轴长为a, 半焦距为c. 利用信息技术, 保持长半轴长a不变, 改变椭圆的半焦距c, 可以发现, c越接近a, 椭圆越扁平. 类似地, 保持c不变, 改变a的大小, 则a越接近c, 椭圆越扁平; 而当a, c扩大或缩小相同倍数时, 椭圆的形状不变. 这样, 利用c和a这两个量, 可以刻画椭圆的扁平程度.
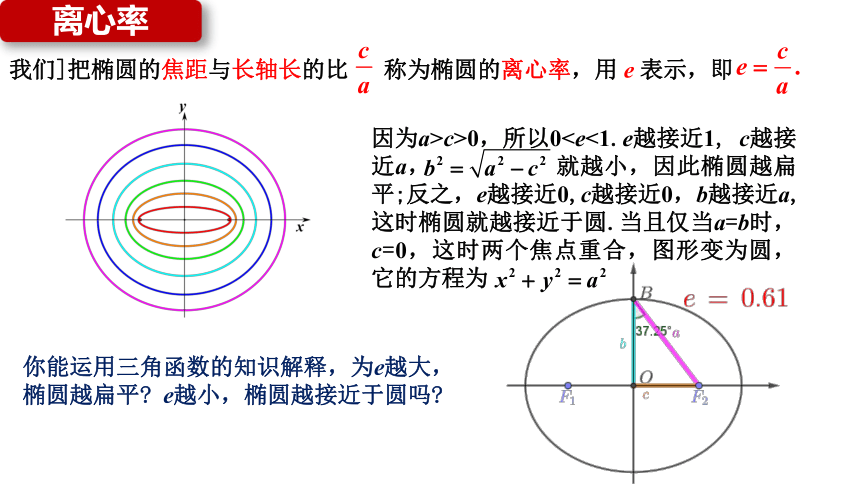
离心率
我们]把椭圆的焦距与长轴长的比 称为椭圆的离心率,用 e 表示,即
因为a>c>0,所以0你能运用三角函数的知识解释,为e越大,椭圆越扁平 e越小,椭圆越接近于圆吗
贰
第二部分
椭圆的几何性质的应用
第二部分
例4 求椭圆16x2+25y2=400的长轴和短轴的长、离心率、焦点和顶点的坐标.
解:
第二部分
例5 如图示, 一种电影放映灯的反射镜面是旋转椭圆面(椭圆绕其对称轴旋转一周形成的曲面)的一部分, 过对称轴的截口BAC是椭圆的一部分, 灯丝位于椭圆的一个焦点F1上, 片门位于另一个焦点F2上, 由椭圆一个焦点F1发出的光线, 经过旋转椭圆面反射后集中到另一个焦点F2 . 已知BC⊥F1F2 , |F1B|=2.8 cm, |F1F2|=4.5 cm. 试建 立适当的平面直角坐标系, 求截口BAC所在椭圆的方程(精确到0.1 cm).
解: 建立如图所示的平面直角坐标系, 设所求椭圆方程为
在Rt△BF1F2中,
由椭圆的性质知,
所以,所求的椭圆方程为
第二部分
例6 动点M(x, y)与定点F(4, 0)的距离和M到定直线l : 的距离的比是常数 求动点M的轨迹.
O
x
y
M
H
F
l
d
解:
椭圆的第二定义
平面内的动点M(x, y)到定点F(c, 0)的距离与它到定直线 的距离的比是常数 则点M的轨迹是椭圆.
其中,定点F(c,0)是椭圆的焦点;
定直线 叫做椭圆的准线;
常数 是椭圆的离心率.
对于焦点 是椭圆
的准线方程是
第二部分
例7
O
x
y
F2
F1
解:
l
l
l
叁
第三部分
课堂练习
1. 你能用圆规作出图中椭圆焦点的位置吗 你的依据是什么
O
x
y
A1
A2
B1
B2
F2
F1
2. 求下列椭圆的焦点坐标:
3. 求适合下列条件的椭圆的标准方程:
4. 求适合下列条件的椭圆的标准方程:
第三部分
5. 求下列直线与椭圆的交点坐标:
6. 经过椭圆 的左焦点F1作倾斜角为60°的直线l,直线l与椭圆相交于A, B两点,求线段AB的长.
解:
O
x
y
M
H
F
l
d
O
x
y
O
x
y
O
m
F2
x
y
F1
m
F2
x
y
F1
O
肆
第四部分
课后小结与预习
焦点位置 x轴 y轴
方程
图形
范围
对称性 顶点
离心率
F1
F2
M
x
y
O
B2
B1
A1
A2
F1
F2
M
x
y
O
B2
B1
A1
A2
焦点位置 x轴 y轴
方程
第二定义 范围
通径 面积公式 (焦点)弦长公式
与一定点的距离和到一定直线的距离之比为常数 ,即
过焦点且垂直于长轴的弦叫通径:
01
02
03
04
05
3.1.1椭圆及标准方程
3.1.2椭圆的简单几何性质
3.2.1双曲线及标准方程
3.2.2双曲线的简单几何性质
3.3.1抛物线及标准方程
06
3.2.2双曲线的简单几何性质
第四部分 预习
3.1.2椭圆的简单几何性质
Conic Section
第三章 圆锥曲线的方程
上节回顾
焦点在x轴的椭圆x2项分母较大.
焦点在y轴的椭圆y2项分母较大.
平面内到两个定点F1,F2的距离的和等
于常数(大于F1F2)的点的轨迹 .
标准方程
相 同 点
焦点位置的判断
不 同 点
图 形
焦点坐标
定 义
a、b、c 的关系
a2-c2=b2
x
y
F1
F2
O
x
y
F1
F2
O
C
I
N
O
C
曲线的简单几何性
通过对曲线的范围、对称性及特殊点的讨论,可以从整体上把握曲线的形状、大小和位置。所以,本章对几种圆锥曲线都是从范围、对称性、顶点及其他特性等方面研究它们的几何性质。
目录
CONTENTS
1
2
3
4
探究椭圆的几何性质
椭圆的几何性质的应用
课堂练习
课后小结与预习
壹
第一部分
探究椭圆的几何性质
与利用直线的方程、圆的方程研究它们的几何性质一样,我们利用椭圆的标准方程研究椭圆的几何性质,包括椭圆的范围、形状、大小、对称性和特殊点等.
下面,我们用椭圆方程 来研究椭圆的几何性质.
1.范围
1. 范围
F1
F2
O
x
y
A1
A2
B1
B2
观察图3.1-7,容易看出椭圆上的点都在一个特定的矩形内,为确定其具体的边界,我们利用方程(代数方法)进行研究.
图3.1-7
对称性
由图可知,椭圆是轴对称图形,也是中心对称图形.
所以,坐标轴是椭圆的对称轴,原点是椭圆的对称中心,椭圆的对称中心(即原点)叫做椭圆的中心.
F1
F2
O
x
y
A1(x,y)
A2(x,-y)
A3(-x,y)
A4(-x,-y)
顶点
F1
F2
O
x
y
A1
说明椭圆与y轴有两个交点, 坐标分别为
A1(-a,0),
A2(a,0).
B1(0,-b),
B2(0,b).
说明椭圆与x轴有两个交点, 坐标分别为
所以椭圆与它的对称轴有四个交点, 这四个交点叫做椭圆的顶点(图3.1-8).
线段A1A2, B1B2分别叫做椭圆的长轴和短轴,它们的长分别等于2a, 2b. a和b分别叫做椭圆的长半轴长和短半轴长.
A2
B1
B2
图3.1-8
2a
2b
你认为椭圆上哪些点比较特殊 为什么 如何得到这些点的坐标
离心率
观察图3.1-9,我们发现,不同椭圆的扁平程度不同,扁平程度是椭圆的重要形状特征,你能用适当的量定量刻画椭圆的扁平程度吗
图3.1-9
如右图示,椭圆 的长半轴长为a, 半焦距为c. 利用信息技术, 保持长半轴长a不变, 改变椭圆的半焦距c, 可以发现, c越接近a, 椭圆越扁平. 类似地, 保持c不变, 改变a的大小, 则a越接近c, 椭圆越扁平; 而当a, c扩大或缩小相同倍数时, 椭圆的形状不变. 这样, 利用c和a这两个量, 可以刻画椭圆的扁平程度.
离心率
我们]把椭圆的焦距与长轴长的比 称为椭圆的离心率,用 e 表示,即
因为a>c>0,所以0
贰
第二部分
椭圆的几何性质的应用
第二部分
例4 求椭圆16x2+25y2=400的长轴和短轴的长、离心率、焦点和顶点的坐标.
解:
第二部分
例5 如图示, 一种电影放映灯的反射镜面是旋转椭圆面(椭圆绕其对称轴旋转一周形成的曲面)的一部分, 过对称轴的截口BAC是椭圆的一部分, 灯丝位于椭圆的一个焦点F1上, 片门位于另一个焦点F2上, 由椭圆一个焦点F1发出的光线, 经过旋转椭圆面反射后集中到另一个焦点F2 . 已知BC⊥F1F2 , |F1B|=2.8 cm, |F1F2|=4.5 cm. 试建 立适当的平面直角坐标系, 求截口BAC所在椭圆的方程(精确到0.1 cm).
解: 建立如图所示的平面直角坐标系, 设所求椭圆方程为
在Rt△BF1F2中,
由椭圆的性质知,
所以,所求的椭圆方程为
第二部分
例6 动点M(x, y)与定点F(4, 0)的距离和M到定直线l : 的距离的比是常数 求动点M的轨迹.
O
x
y
M
H
F
l
d
解:
椭圆的第二定义
平面内的动点M(x, y)到定点F(c, 0)的距离与它到定直线 的距离的比是常数 则点M的轨迹是椭圆.
其中,定点F(c,0)是椭圆的焦点;
定直线 叫做椭圆的准线;
常数 是椭圆的离心率.
对于焦点 是椭圆
的准线方程是
第二部分
例7
O
x
y
F2
F1
解:
l
l
l
叁
第三部分
课堂练习
1. 你能用圆规作出图中椭圆焦点的位置吗 你的依据是什么
O
x
y
A1
A2
B1
B2
F2
F1
2. 求下列椭圆的焦点坐标:
3. 求适合下列条件的椭圆的标准方程:
4. 求适合下列条件的椭圆的标准方程:
第三部分
5. 求下列直线与椭圆的交点坐标:
6. 经过椭圆 的左焦点F1作倾斜角为60°的直线l,直线l与椭圆相交于A, B两点,求线段AB的长.
解:
O
x
y
M
H
F
l
d
O
x
y
O
x
y
O
m
F2
x
y
F1
m
F2
x
y
F1
O
肆
第四部分
课后小结与预习
焦点位置 x轴 y轴
方程
图形
范围
对称性 顶点
离心率
F1
F2
M
x
y
O
B2
B1
A1
A2
F1
F2
M
x
y
O
B2
B1
A1
A2
焦点位置 x轴 y轴
方程
第二定义 范围
通径 面积公式 (焦点)弦长公式
与一定点的距离和到一定直线的距离之比为常数 ,即
过焦点且垂直于长轴的弦叫通径:
01
02
03
04
05
3.1.1椭圆及标准方程
3.1.2椭圆的简单几何性质
3.2.1双曲线及标准方程
3.2.2双曲线的简单几何性质
3.3.1抛物线及标准方程
06
3.2.2双曲线的简单几何性质
第四部分 预习
