2022-2023学年人教版九年级数学上册 23.1 图形的旋转 课堂训练试卷 (word版含答案)
文档属性
| 名称 | 2022-2023学年人教版九年级数学上册 23.1 图形的旋转 课堂训练试卷 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 681.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-06 06:40:24 | ||
图片预览



文档简介
2022-2023学年度人教版初中九年级数学课堂提升训练试卷
第二十三章 旋转
23.1 图形的旋转
1. 下列运动形式属于旋转的是( )
A.火箭腾空而起
B.“复兴号”高铁在铁轨上飞驰
C.时钟上指针的转动
D.冰球在冰面上滚动
2.如图所示的运动员只经过旋转不能得到的是( )
3.如图,△ABD经过旋转后到达△ACE的位置,∠BAC=30°,下列说法不正确的是( )
A.点A是旋转中心
B.∠DAC是一个旋转角
C.若是顺时针旋转,则至少旋转了330°
D.若是逆时针旋转,则至少旋转了30°
4.如图,将三角形ABC绕点A逆时针旋转85°得到三角形AB'C',若∠C'AB'=60°,则∠CAB'=( )
A.60° B.85°
C.25° D.15°
5.如图,将△ABC绕点A逆时针旋转55°,得到△ADE,若∠E=70°且AD⊥BC于点F,则∠BAC的度数为( )
A.65° B.70° C.75° D.80°
6.如图,在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=8,BD=7,则△AED的周长是( )
A.10 B.12 C.14 D.15
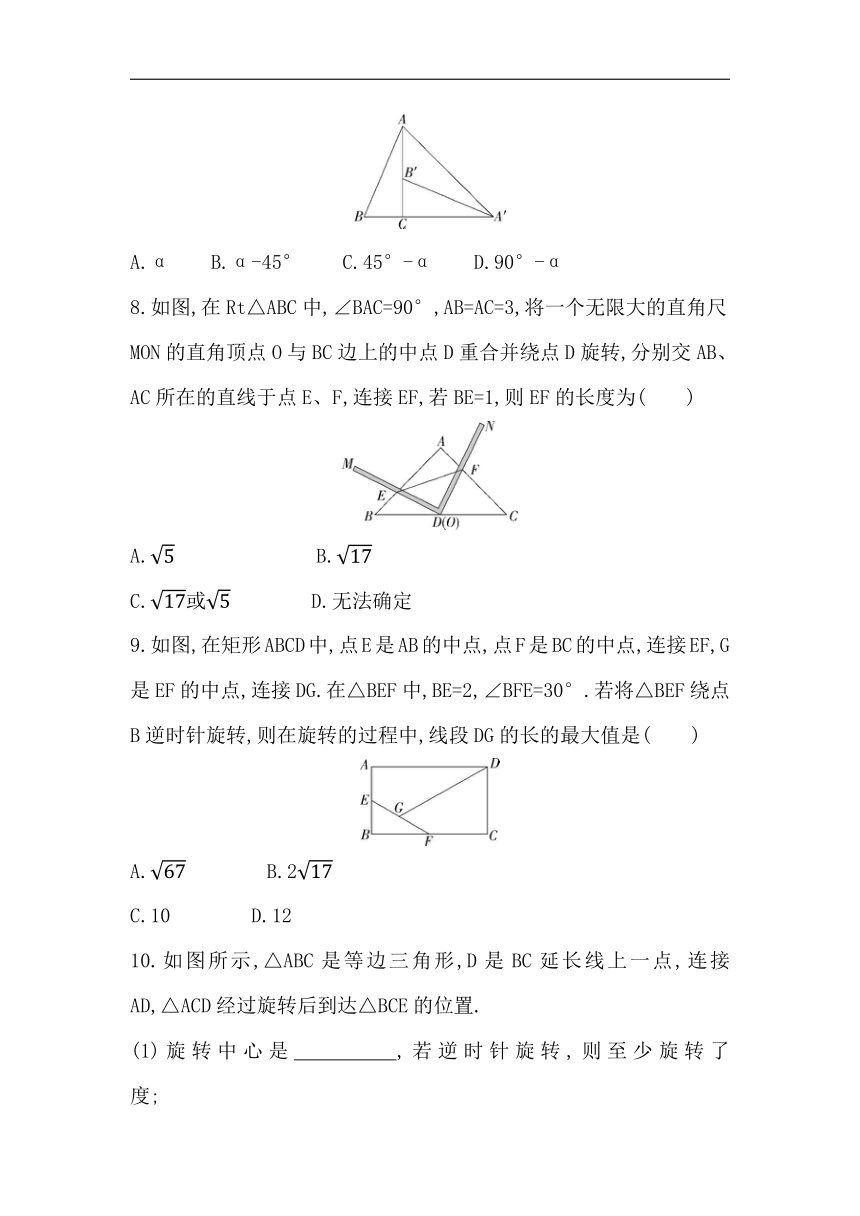
7.如图,在△ABC中,∠ACB=90°,∠BAC=α,将△ABC绕点C顺时针旋转90°得到△A'B'C,点B的对应点B'在边AC上(不与点A,C重合),则∠AA'B'的度数为( )
A.α B.α-45° C.45°-α D.90°-α
8.如图,在Rt△ABC中,∠BAC=90°,AB=AC=3,将一个无限大的直角尺MON的直角顶点O与BC边上的中点D重合并绕点D旋转,分别交AB、AC所在的直线于点E、F,连接EF,若BE=1,则EF的长度为( )
A. B.
C.或 D.无法确定
9.如图,在矩形ABCD中,点E是AB的中点,点F是BC的中点,连接EF,G是EF的中点,连接DG.在△BEF中,BE=2,∠BFE=30°.若将△BEF绕点B逆时针旋转,则在旋转的过程中,线段DG的长的最大值是( )
A. B.2
C.10 D.12
10.如图所示,△ABC是等边三角形,D是BC延长线上一点,连接AD,△ACD经过旋转后到达△BCE的位置.
(1)旋转中心是 ,若逆时针旋转,则至少旋转了 度;
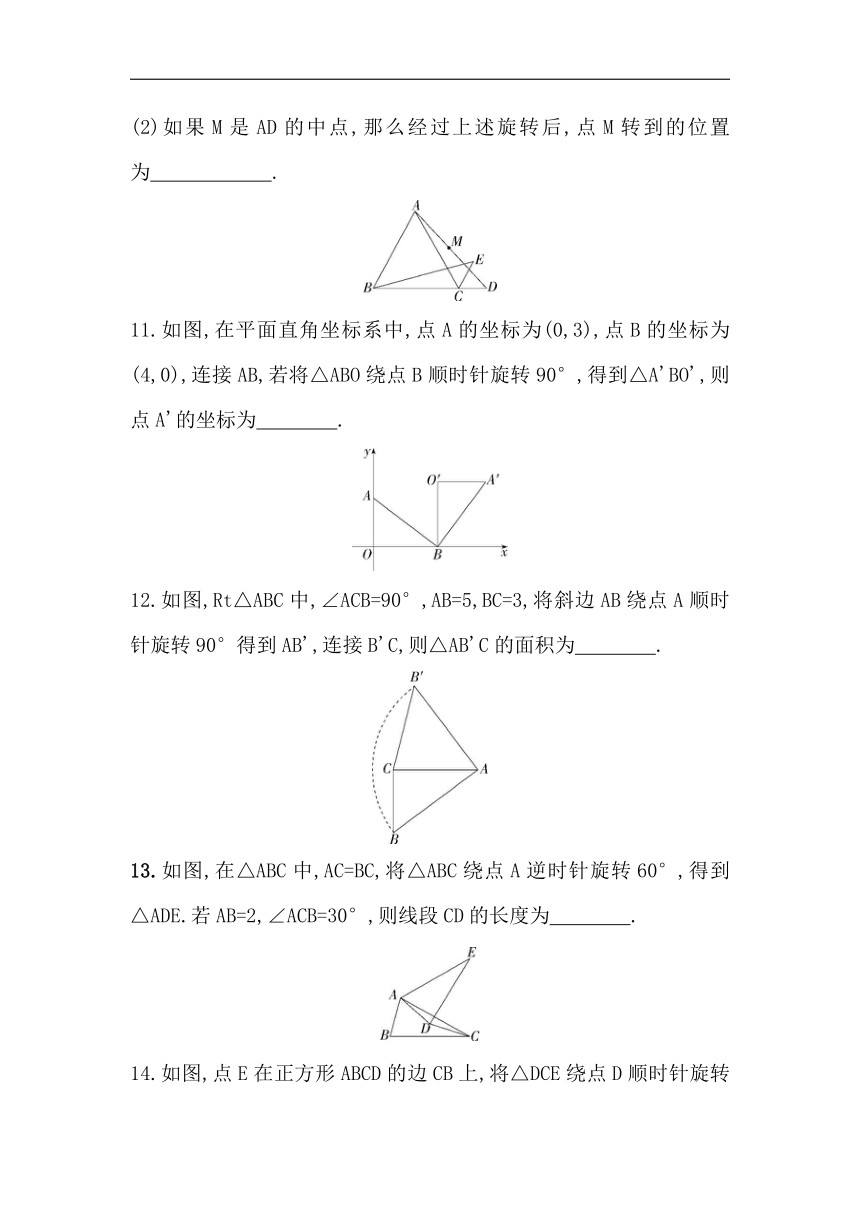
(2)如果M是AD的中点,那么经过上述旋转后,点M转到的位置为 .
11.如图,在平面直角坐标系中,点A的坐标为(0,3),点B的坐标为(4,0),连接AB,若将△ABO绕点B顺时针旋转90°,得到△A'BO',则点A'的坐标为 .
12.如图,Rt△ABC中,∠ACB=90°,AB=5,BC=3,将斜边AB绕点A顺时针旋转90°得到AB',连接B'C,则△AB'C的面积为 .
13.如图,在△ABC中,AC=BC,将△ABC绕点A逆时针旋转60°,得到△ADE.若AB=2,∠ACB=30°,则线段CD的长度为 .
14.如图,点E在正方形ABCD的边CB上,将△DCE绕点D顺时针旋转90°到△DAF的位置,连接EF,过点D作EF的垂线,垂足为点H,与AB交于点G,若AG=4,BG=3,则BE的长为 .
15.如图,在四边形ABCD中,AD∥BC,AD=AB=CD=4,∠B=∠C=60°,M是线段BC的中点,将△MDC绕点M旋转,得到△MD'C',当MD'与AB交于点E,且MC'与AD交于点F时,得到以点E、F、A为顶点的△AEF.在此过程中,△AEF的周长的最小值是 .
16.如图,在△ABC中,∠ACB=90°,∠BAC=30°,AB=2.若点P是△ABC内一点,则PA+PB+PC的最小值为 .
17.如图,以点O为旋转中心,将△ABC按顺时针方向旋转60°,作出旋转后的图形(不用写作法).
18.如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,直线MN与直线GH交于点O,△ABC的顶点均在格点上.
(1)画出△ABC关于直线MN对称的△A1B1C1;
(2)画出将△ABC绕点O按逆时针方向旋转90°所得到的△A2B2C2.
19.如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(1,4),B(4,1),C(4,3).
(1)画出将△ABC向左平移5个单位长度得到的△A1B1C1;
(2)画出将△ABC绕原点O顺时针旋转90°得到的△A2B2C2.
答案全解全析
基础过关全练
1.C 选项A、B中的运动可看作是平移;选项D中的运动是滚动,不是旋转;选项C中的运动是旋转.
2.C 选项A、B、D中的运动员都可以通过旋转题图得到,而选项C中的运动员是通过翻折题图得到的.故选C.
3.B 由题图可知,旋转前后点A没有发生变化,故点A是旋转中心.易知∠BAC和∠DAE都是旋转角,∠DAC不是旋转角.∵∠BAC=30°,∴逆时针旋转时,至少旋转了30°,顺时针旋转时,至少旋转了330°.故选B.
4.C ∵将△ABC绕点A逆时针旋转85°得到△AB'C',∴∠C'AC=85°.
∵∠C'AB'=60°,
∴∠CAB'=∠C'AC-∠C'AB'=85°-60°=25°.故选C.
5.C ∵将△ABC绕点A逆时针旋转55°得到△ADE,∠E=70°,
∴∠BAD=55°,∠ACB=∠E=70°,∵AD⊥BC,∴∠DAC=20°,∴∠BAC=∠BAD+∠DAC=75°.
D ∵将△BCD绕点B逆时针旋转60°得到△BAE,
∴BD=BE,∠DBE=60°,CD=AE,∴△DBE是等边三角形,∴DE=BD=7,
∴△AED的周长=AE+AD+DE=CD+AD+DE=8+7=15.
7.C ∵将△ABC绕点C顺时针旋转90°得到△A'B'C,
∴AC=A'C,∠BAC=∠CA'B',∠ACA'=90°,∴△ACA'是等腰直角三角形,
∴∠CA'A=45°.∵∠BAC=α,∴∠CA'B'=α,∴∠AA'B'=45°-α.
8.C 分两种情况讨论:①如图1,当点E、F在线段AB、AC上时,连接AD,
∵AB=AC,∠BAC=90°,D为BC的中点,
∴BD=AD=CD,AD⊥BC,∠B=∠1=∠2=45°.
又∵∠EDF=90°,
∴∠BDE=∠ADF,∴△BDE≌△ADF(ASA),
∴AF=BE=1.∵AE=3-1=2,
∴在Rt△AEF中,由勾股定理得EF==.
图1
②如图2,当点E、F在AB、CA的延长线上时,连接AD,同理可证△EBD≌△FAD,∴AF=BE=1.又∵AE=AB+BE=4,∴EF==.
综上所述,EF=或.
图2
9.C 如图,将△BEF旋转到图中位置,连接BD、BG,∵在△BEF中,
∠EBF=90°,BE=2,∠BFE=30°,∴EF=2BE=4,BF=2.∵旋转前点E是AB的中点,点F是BC的中点,∴CD=AB=2BE=4,BC=2BF=4,∴BD=8.∵在Rt△BEF中,点G是EF的中点,∴BG=EF=2,∴在△BEF旋转的过程中,BG的长不变,∵在△DBG中,BG+BD>GD,∴当D,B,G三点共线,且D、G两点在点B的两侧时,DG的长最大,此时,DG=BG+BD=2+8=10,∴DG的长的最大值为10.故选C.
10.解析 (1)点C;60.
(2)BE的中点.
11.(7,4)
解析 如图,作A'C⊥x轴于点C,由题可知∠O'=90°,O'B⊥x轴,∴四边形O'BCA'为矩形,
∴BC=A'O'=OA=3,A'C=O'B=OB=4,∴OC=OB+BC=7,∴点A'的坐标为(7,4).
12.8
解析 如图,作B'H⊥AC于H,∴∠AHB'=90°,∴∠HAB'+∠HB'A=90°,由题可知,∠BAC+∠HAB'=∠BAB'=90°,∴∠HB'A=∠BAC.
又∵∠ACB=∠AHB',AB=AB',∴△ACB≌△B'HA,∴AC=B'H.
∵∠ACB=90°,AB=5,BC=3,∴AC===4,∴B'H=AC=4,
∴S△AB'C=AC·B'H=×4×4=8.
13.2
解析 如图,连接CE,∵△ABC绕点A逆时针旋转60°,得到△ADE,
∴AD=AB=2,AE=AC,∠CAE=60°,∠AED=∠ACB=30°,∴△ACE为等边三角形,
∴∠AEC=60°,∵∠AED=30°,∴ED平分∠AEC,∴DE垂直平分AC,∴DC=DA=2.
14.
解析 如图,连接EG,∵将△DCE绕点D顺时针旋转90°到△DAF的位置,
∴DF=DE,AF=CE,∠EDF=90°,
∴△DEF为等腰直角三角形,
∵DG⊥EF,∴EH=FH,∴DG垂直平分EF,
∴FG=GE.∵AG=4,BG=3,∴BC=AB=7.设BE=x,则AF=CE=7-x,
∴GE=FG=4+7-x=11-x.
∵∠B=90°,∴GE2=GB2+BE2,
∴(11-x)2=9+x2,解得x=,∴BE=.
15.4+2
解析 如图,连接AM,过点D作DP⊥BC于点P,过点A作AQ⊥BC于点Q,则AQ∥DP.∵AD∥BC,
∴四边形ADPQ是平行四边形,
∴QP=AD=4,∵∠C=∠B=60°,
∴∠BAQ=∠CDP=30°,
∴CP=CD=2,BQ=AB=2,
∴BC=2+2+4=8.
∵点M是BC的中点,
∴CM=BM=4,
∴CD=CM.易知△MCD,△MAB,△MAD和△MC'D'是等边三角形,
∴∠BMA=∠BME+∠AME=60°,∠EMF=∠AMF+∠AME=60°,
∴∠BME=∠AMF.在△BME与△AMF中,
∴△BME≌△AMF(ASA),
∴BE=AF,ME=MF,
∴AE+AF=AE+BE=AB.
∵∠EMF=60°,
∴△EMF是等边三角形,EF=MF.
∵MF的最小值为点M到AD的距离,等于DP的长,又易得DP=2,
∴EF的最小值是2,
∵△AEF的周长=AE+AF+EF=AB+EF,
∴△AEF的周长的最小值为4+2.
16.
解析 如图,将△ACP绕点A逆时针旋转60°得到△AC'P',连接PP',BC',由旋转的性质可得
AP'=AP,AC'=AC,P'C'=PC,∠CAC'=∠PAP'=60°,
∴△APP'是等边三角形,
∴PP'=AP,
∴PA+PB+PC=PP'+PB+P'C',
∴当B、P、P'、C'在同一条直线上时,PA+PB+PC的值最小.在△BAC中,
∵∠ACB=90°,∠BAC=30°,AB=2,∴BC=1,
∴AC'=AC=.∵∠BAC=30°,∠CAC'=60°,
∴∠BAC'=90°,∴BC'===,
∴PA+PB+PC的最小值为.
17.解析 如图所示,△A'B'C'即为所求.
18.解析 (1)如图所示,△A1B1C1即为所求.
(2)如图所示,△A2B2C2即为所求.
19.解析 (1)如图所示,△A1B1C1即为所求.
(2)如图所示,△A2B2C2即为所求.
第二十三章 旋转
23.1 图形的旋转
1. 下列运动形式属于旋转的是( )
A.火箭腾空而起
B.“复兴号”高铁在铁轨上飞驰
C.时钟上指针的转动
D.冰球在冰面上滚动
2.如图所示的运动员只经过旋转不能得到的是( )
3.如图,△ABD经过旋转后到达△ACE的位置,∠BAC=30°,下列说法不正确的是( )
A.点A是旋转中心
B.∠DAC是一个旋转角
C.若是顺时针旋转,则至少旋转了330°
D.若是逆时针旋转,则至少旋转了30°
4.如图,将三角形ABC绕点A逆时针旋转85°得到三角形AB'C',若∠C'AB'=60°,则∠CAB'=( )
A.60° B.85°
C.25° D.15°
5.如图,将△ABC绕点A逆时针旋转55°,得到△ADE,若∠E=70°且AD⊥BC于点F,则∠BAC的度数为( )
A.65° B.70° C.75° D.80°
6.如图,在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=8,BD=7,则△AED的周长是( )
A.10 B.12 C.14 D.15
7.如图,在△ABC中,∠ACB=90°,∠BAC=α,将△ABC绕点C顺时针旋转90°得到△A'B'C,点B的对应点B'在边AC上(不与点A,C重合),则∠AA'B'的度数为( )
A.α B.α-45° C.45°-α D.90°-α
8.如图,在Rt△ABC中,∠BAC=90°,AB=AC=3,将一个无限大的直角尺MON的直角顶点O与BC边上的中点D重合并绕点D旋转,分别交AB、AC所在的直线于点E、F,连接EF,若BE=1,则EF的长度为( )
A. B.
C.或 D.无法确定
9.如图,在矩形ABCD中,点E是AB的中点,点F是BC的中点,连接EF,G是EF的中点,连接DG.在△BEF中,BE=2,∠BFE=30°.若将△BEF绕点B逆时针旋转,则在旋转的过程中,线段DG的长的最大值是( )
A. B.2
C.10 D.12
10.如图所示,△ABC是等边三角形,D是BC延长线上一点,连接AD,△ACD经过旋转后到达△BCE的位置.
(1)旋转中心是 ,若逆时针旋转,则至少旋转了 度;
(2)如果M是AD的中点,那么经过上述旋转后,点M转到的位置为 .
11.如图,在平面直角坐标系中,点A的坐标为(0,3),点B的坐标为(4,0),连接AB,若将△ABO绕点B顺时针旋转90°,得到△A'BO',则点A'的坐标为 .
12.如图,Rt△ABC中,∠ACB=90°,AB=5,BC=3,将斜边AB绕点A顺时针旋转90°得到AB',连接B'C,则△AB'C的面积为 .
13.如图,在△ABC中,AC=BC,将△ABC绕点A逆时针旋转60°,得到△ADE.若AB=2,∠ACB=30°,则线段CD的长度为 .
14.如图,点E在正方形ABCD的边CB上,将△DCE绕点D顺时针旋转90°到△DAF的位置,连接EF,过点D作EF的垂线,垂足为点H,与AB交于点G,若AG=4,BG=3,则BE的长为 .
15.如图,在四边形ABCD中,AD∥BC,AD=AB=CD=4,∠B=∠C=60°,M是线段BC的中点,将△MDC绕点M旋转,得到△MD'C',当MD'与AB交于点E,且MC'与AD交于点F时,得到以点E、F、A为顶点的△AEF.在此过程中,△AEF的周长的最小值是 .
16.如图,在△ABC中,∠ACB=90°,∠BAC=30°,AB=2.若点P是△ABC内一点,则PA+PB+PC的最小值为 .
17.如图,以点O为旋转中心,将△ABC按顺时针方向旋转60°,作出旋转后的图形(不用写作法).
18.如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,直线MN与直线GH交于点O,△ABC的顶点均在格点上.
(1)画出△ABC关于直线MN对称的△A1B1C1;
(2)画出将△ABC绕点O按逆时针方向旋转90°所得到的△A2B2C2.
19.如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(1,4),B(4,1),C(4,3).
(1)画出将△ABC向左平移5个单位长度得到的△A1B1C1;
(2)画出将△ABC绕原点O顺时针旋转90°得到的△A2B2C2.
答案全解全析
基础过关全练
1.C 选项A、B中的运动可看作是平移;选项D中的运动是滚动,不是旋转;选项C中的运动是旋转.
2.C 选项A、B、D中的运动员都可以通过旋转题图得到,而选项C中的运动员是通过翻折题图得到的.故选C.
3.B 由题图可知,旋转前后点A没有发生变化,故点A是旋转中心.易知∠BAC和∠DAE都是旋转角,∠DAC不是旋转角.∵∠BAC=30°,∴逆时针旋转时,至少旋转了30°,顺时针旋转时,至少旋转了330°.故选B.
4.C ∵将△ABC绕点A逆时针旋转85°得到△AB'C',∴∠C'AC=85°.
∵∠C'AB'=60°,
∴∠CAB'=∠C'AC-∠C'AB'=85°-60°=25°.故选C.
5.C ∵将△ABC绕点A逆时针旋转55°得到△ADE,∠E=70°,
∴∠BAD=55°,∠ACB=∠E=70°,∵AD⊥BC,∴∠DAC=20°,∴∠BAC=∠BAD+∠DAC=75°.
D ∵将△BCD绕点B逆时针旋转60°得到△BAE,
∴BD=BE,∠DBE=60°,CD=AE,∴△DBE是等边三角形,∴DE=BD=7,
∴△AED的周长=AE+AD+DE=CD+AD+DE=8+7=15.
7.C ∵将△ABC绕点C顺时针旋转90°得到△A'B'C,
∴AC=A'C,∠BAC=∠CA'B',∠ACA'=90°,∴△ACA'是等腰直角三角形,
∴∠CA'A=45°.∵∠BAC=α,∴∠CA'B'=α,∴∠AA'B'=45°-α.
8.C 分两种情况讨论:①如图1,当点E、F在线段AB、AC上时,连接AD,
∵AB=AC,∠BAC=90°,D为BC的中点,
∴BD=AD=CD,AD⊥BC,∠B=∠1=∠2=45°.
又∵∠EDF=90°,
∴∠BDE=∠ADF,∴△BDE≌△ADF(ASA),
∴AF=BE=1.∵AE=3-1=2,
∴在Rt△AEF中,由勾股定理得EF==.
图1
②如图2,当点E、F在AB、CA的延长线上时,连接AD,同理可证△EBD≌△FAD,∴AF=BE=1.又∵AE=AB+BE=4,∴EF==.
综上所述,EF=或.
图2
9.C 如图,将△BEF旋转到图中位置,连接BD、BG,∵在△BEF中,
∠EBF=90°,BE=2,∠BFE=30°,∴EF=2BE=4,BF=2.∵旋转前点E是AB的中点,点F是BC的中点,∴CD=AB=2BE=4,BC=2BF=4,∴BD=8.∵在Rt△BEF中,点G是EF的中点,∴BG=EF=2,∴在△BEF旋转的过程中,BG的长不变,∵在△DBG中,BG+BD>GD,∴当D,B,G三点共线,且D、G两点在点B的两侧时,DG的长最大,此时,DG=BG+BD=2+8=10,∴DG的长的最大值为10.故选C.
10.解析 (1)点C;60.
(2)BE的中点.
11.(7,4)
解析 如图,作A'C⊥x轴于点C,由题可知∠O'=90°,O'B⊥x轴,∴四边形O'BCA'为矩形,
∴BC=A'O'=OA=3,A'C=O'B=OB=4,∴OC=OB+BC=7,∴点A'的坐标为(7,4).
12.8
解析 如图,作B'H⊥AC于H,∴∠AHB'=90°,∴∠HAB'+∠HB'A=90°,由题可知,∠BAC+∠HAB'=∠BAB'=90°,∴∠HB'A=∠BAC.
又∵∠ACB=∠AHB',AB=AB',∴△ACB≌△B'HA,∴AC=B'H.
∵∠ACB=90°,AB=5,BC=3,∴AC===4,∴B'H=AC=4,
∴S△AB'C=AC·B'H=×4×4=8.
13.2
解析 如图,连接CE,∵△ABC绕点A逆时针旋转60°,得到△ADE,
∴AD=AB=2,AE=AC,∠CAE=60°,∠AED=∠ACB=30°,∴△ACE为等边三角形,
∴∠AEC=60°,∵∠AED=30°,∴ED平分∠AEC,∴DE垂直平分AC,∴DC=DA=2.
14.
解析 如图,连接EG,∵将△DCE绕点D顺时针旋转90°到△DAF的位置,
∴DF=DE,AF=CE,∠EDF=90°,
∴△DEF为等腰直角三角形,
∵DG⊥EF,∴EH=FH,∴DG垂直平分EF,
∴FG=GE.∵AG=4,BG=3,∴BC=AB=7.设BE=x,则AF=CE=7-x,
∴GE=FG=4+7-x=11-x.
∵∠B=90°,∴GE2=GB2+BE2,
∴(11-x)2=9+x2,解得x=,∴BE=.
15.4+2
解析 如图,连接AM,过点D作DP⊥BC于点P,过点A作AQ⊥BC于点Q,则AQ∥DP.∵AD∥BC,
∴四边形ADPQ是平行四边形,
∴QP=AD=4,∵∠C=∠B=60°,
∴∠BAQ=∠CDP=30°,
∴CP=CD=2,BQ=AB=2,
∴BC=2+2+4=8.
∵点M是BC的中点,
∴CM=BM=4,
∴CD=CM.易知△MCD,△MAB,△MAD和△MC'D'是等边三角形,
∴∠BMA=∠BME+∠AME=60°,∠EMF=∠AMF+∠AME=60°,
∴∠BME=∠AMF.在△BME与△AMF中,
∴△BME≌△AMF(ASA),
∴BE=AF,ME=MF,
∴AE+AF=AE+BE=AB.
∵∠EMF=60°,
∴△EMF是等边三角形,EF=MF.
∵MF的最小值为点M到AD的距离,等于DP的长,又易得DP=2,
∴EF的最小值是2,
∵△AEF的周长=AE+AF+EF=AB+EF,
∴△AEF的周长的最小值为4+2.
16.
解析 如图,将△ACP绕点A逆时针旋转60°得到△AC'P',连接PP',BC',由旋转的性质可得
AP'=AP,AC'=AC,P'C'=PC,∠CAC'=∠PAP'=60°,
∴△APP'是等边三角形,
∴PP'=AP,
∴PA+PB+PC=PP'+PB+P'C',
∴当B、P、P'、C'在同一条直线上时,PA+PB+PC的值最小.在△BAC中,
∵∠ACB=90°,∠BAC=30°,AB=2,∴BC=1,
∴AC'=AC=.∵∠BAC=30°,∠CAC'=60°,
∴∠BAC'=90°,∴BC'===,
∴PA+PB+PC的最小值为.
17.解析 如图所示,△A'B'C'即为所求.
18.解析 (1)如图所示,△A1B1C1即为所求.
(2)如图所示,△A2B2C2即为所求.
19.解析 (1)如图所示,△A1B1C1即为所求.
(2)如图所示,△A2B2C2即为所求.
同课章节目录
