2022-2023学年人教版九年级数学上册23.2.2中心对称图形 课堂训练试卷(word版含答案)
文档属性
| 名称 | 2022-2023学年人教版九年级数学上册23.2.2中心对称图形 课堂训练试卷(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 316.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-06 07:32:06 | ||
图片预览


文档简介
2022-2023学年度人教版初中九年级数学课堂提升训练试卷
第二十三章 旋转
23.2 中心对称
23.2.2 中心对称图形
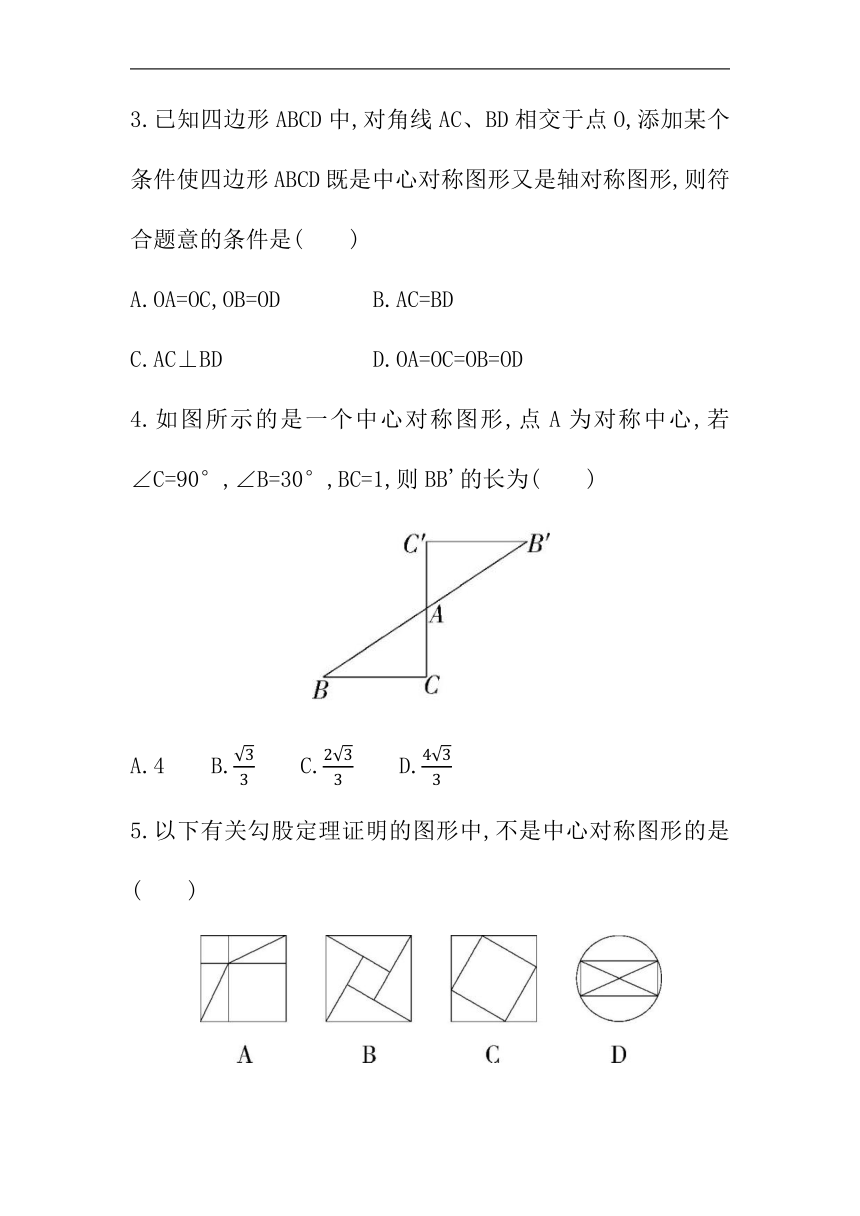
下列四幅图案是四所大学校徽的主体标识,其中是中心对称图形的是( )
2.下列图形中,是中心对称图形但不是轴对称图形的是 ( )
A. B.
C. D.
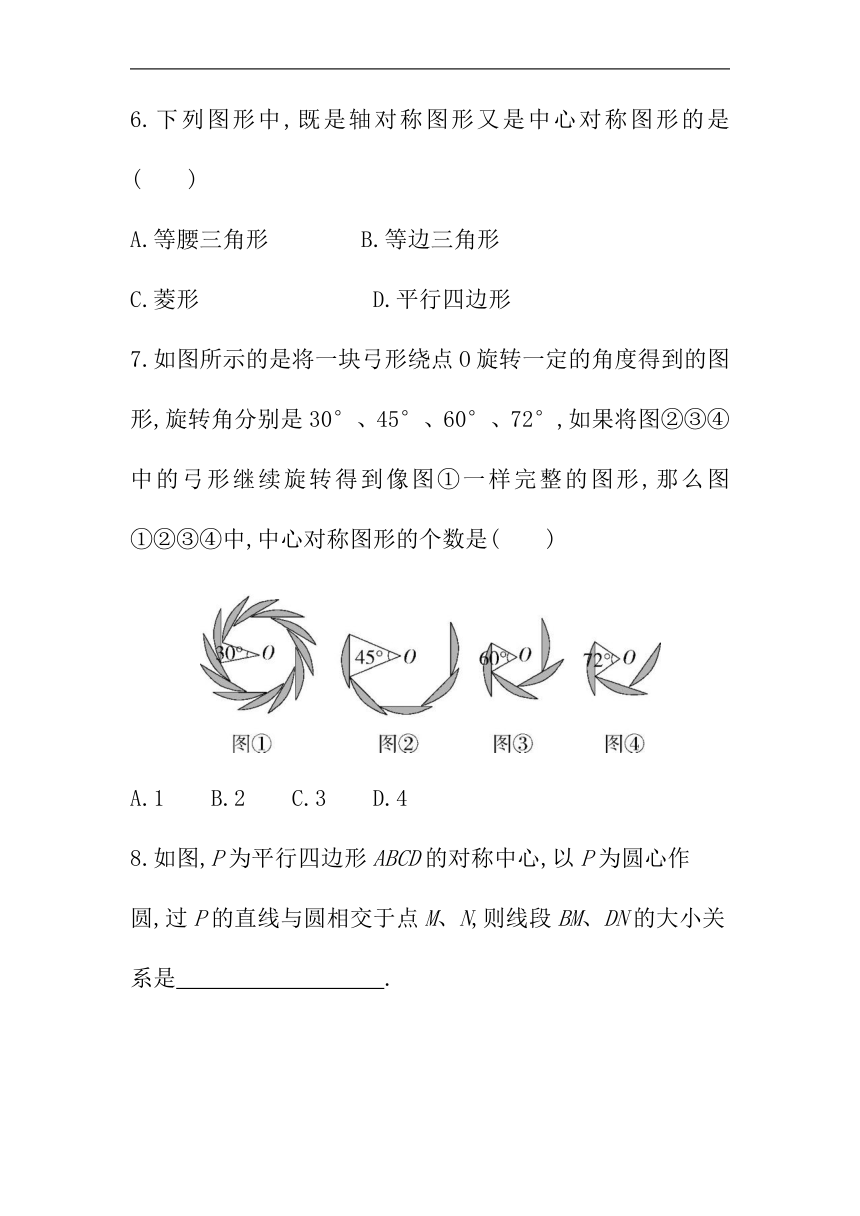
3.已知四边形ABCD中,对角线AC、BD相交于点O,添加某个条件使四边形ABCD既是中心对称图形又是轴对称图形,则符合题意的条件是( )
A.OA=OC,OB=OD B.AC=BD
C.AC⊥BD D.OA=OC=OB=OD
4.如图所示的是一个中心对称图形,点A为对称中心,若∠C=90°,∠B=30°,BC=1,则BB'的长为( )
A.4 B. C. D.
5.以下有关勾股定理证明的图形中,不是中心对称图形的是( )
6.下列图形中,既是轴对称图形又是中心对称图形的是( )
A.等腰三角形 B.等边三角形
C.菱形 D.平行四边形
7.如图所示的是将一块弓形绕点O旋转一定的角度得到的图形,旋转角分别是30°、45°、60°、72°,如果将图②③④中的弓形继续旋转得到像图①一样完整的图形,那么图①②③④中,中心对称图形的个数是( )
A.1 B.2 C.3 D.4
8.如图,P为平行四边形ABCD的对称中心,以P为圆心作
圆,过P的直线与圆相交于点M、N,则线段BM、DN的大小关
系是 .
9.从数学对称的角度看下面的几组大写英文字母:①ANEG;②KBXM;③XIHO;④HWDZ.不同于另外三组的一组是 ,这一组的特点是 .
10.有下列平面图形:线段、等腰直角三角形、等边三角形、平行四边形、长方形、正方形、圆,其中轴对称图形有a个,中心对称图形有b个,则a2+b3的值为 .
11.在一次数学社团活动中,小明设计了一个社团标识,如图所示,正方形ABCD与折线DE—EF—FB构成了一个中心对称图形,且DE⊥EF,AD=50,DE比EF长25,那么EF的长是 .
12. 有一块如图所示的钢板,如何用一条直线将其分为面积相等的两部分
答案全解全析
1.C 观察图形可知,选项C中的图形绕中心旋转180°后能与自身重合,是中心对称图形,选项A、B、D中的图形只是轴对称图形.
2. B 选项A、D中的图形都是轴对称图形,但不是中心对称图形;选项B中的图形是中心对称图形,但不是轴对称图形;选项C中的图形既是轴对称图形,又是中心对称图形.
3.D 添加选项A中的条件,可得四边形ABCD是平行四边形,是中心对称图形,不一定是轴对称图形;添加选项B或C中的条件,不一定是中心对称图形,也不一定是轴对称图形;添加选项D中的条件,可得四边形ABCD是矩形,既是中心对称图形又是轴对称图形.故选D.
4.D ∵∠C=90°,∠B=30°,∴AB=2AC.∵BC=1,∴由勾股定理可得AB=,又题图为一个中心对称图形,点A为对称中心,∴BB'=2AB=.故选D.
5.A 选项A中的图形是轴对称图形,不是中心对称图形;选项B、C中的图形是中心对称图形,不是轴对称图形;选项D中的图形既是中心对称图形,又是轴对称图形.
6.C 菱形既是轴对称图形,又是中心对称图形.故选C.
7.C 得到的完整图形中,图①由12个弓形组成,图②由8个弓形组成,图③由6个弓形组成,图④由5个弓形组成,所以图①②③是中心对称图形,图④不是中心对称图形.故选C.
8.如图,连接BD,
∵P为平行四边形ABCD的对称中心,
∴P是平行四边形的两条对角线的交点,即BD必过点P,且BP=DP,
∵P为圆心,且过P的直线与圆相交于点M、N,∴PN=PM,又∵
∠DPN=∠BPM,
∴△PDN≌△PBM,∴BM=DN.
9.③;每个字母既可看作轴对称图形,又可看作中心对称图形
解析 ①中的字母,可看作轴对称图形的是A、E,可看作中心对称图形的是N;②中的字母,可看作轴对称图形的是K、B、X、M,其中X还可看作中心对称图形;③中的所有字母既可看作轴对称图形,又可看作中心对称图形;④中的字母,可看作轴对称图形的是H、W、D,可看作中心对称图形的是H、Z.故不同于另外三组的一组是③,这一组的特点是每个字母既可看作轴对称图形,又可看作中心对称图形.
10.161
解析 轴对称图形:线段、等腰直角三角形、等边三角形、长方形、正方形、圆,共6个,∴a=6;
中心对称图形:线段、平行四边形、长方形、正方形、圆,共5个,
∴b=5.∴a2+b3=62+53=161.
11.10
解析 如图,连接BD,与EF交于点O,∵正方形ABCD与折线DE—EF—FB构成了中心对称图形,∴OE=EF,OD=BD,∵AD=50,∴BD==50,∴OD=25.设EF=2x,则OE=x,DE=2x+25,在Rt△DOE中,x2+(2x+25)2=(25)2,解得x=5或x=-25(舍去),
∴EF=5×2=10.
12.如图,有三种画法.
第二十三章 旋转
23.2 中心对称
23.2.2 中心对称图形
下列四幅图案是四所大学校徽的主体标识,其中是中心对称图形的是( )
2.下列图形中,是中心对称图形但不是轴对称图形的是 ( )
A. B.
C. D.
3.已知四边形ABCD中,对角线AC、BD相交于点O,添加某个条件使四边形ABCD既是中心对称图形又是轴对称图形,则符合题意的条件是( )
A.OA=OC,OB=OD B.AC=BD
C.AC⊥BD D.OA=OC=OB=OD
4.如图所示的是一个中心对称图形,点A为对称中心,若∠C=90°,∠B=30°,BC=1,则BB'的长为( )
A.4 B. C. D.
5.以下有关勾股定理证明的图形中,不是中心对称图形的是( )
6.下列图形中,既是轴对称图形又是中心对称图形的是( )
A.等腰三角形 B.等边三角形
C.菱形 D.平行四边形
7.如图所示的是将一块弓形绕点O旋转一定的角度得到的图形,旋转角分别是30°、45°、60°、72°,如果将图②③④中的弓形继续旋转得到像图①一样完整的图形,那么图①②③④中,中心对称图形的个数是( )
A.1 B.2 C.3 D.4
8.如图,P为平行四边形ABCD的对称中心,以P为圆心作
圆,过P的直线与圆相交于点M、N,则线段BM、DN的大小关
系是 .
9.从数学对称的角度看下面的几组大写英文字母:①ANEG;②KBXM;③XIHO;④HWDZ.不同于另外三组的一组是 ,这一组的特点是 .
10.有下列平面图形:线段、等腰直角三角形、等边三角形、平行四边形、长方形、正方形、圆,其中轴对称图形有a个,中心对称图形有b个,则a2+b3的值为 .
11.在一次数学社团活动中,小明设计了一个社团标识,如图所示,正方形ABCD与折线DE—EF—FB构成了一个中心对称图形,且DE⊥EF,AD=50,DE比EF长25,那么EF的长是 .
12. 有一块如图所示的钢板,如何用一条直线将其分为面积相等的两部分
答案全解全析
1.C 观察图形可知,选项C中的图形绕中心旋转180°后能与自身重合,是中心对称图形,选项A、B、D中的图形只是轴对称图形.
2. B 选项A、D中的图形都是轴对称图形,但不是中心对称图形;选项B中的图形是中心对称图形,但不是轴对称图形;选项C中的图形既是轴对称图形,又是中心对称图形.
3.D 添加选项A中的条件,可得四边形ABCD是平行四边形,是中心对称图形,不一定是轴对称图形;添加选项B或C中的条件,不一定是中心对称图形,也不一定是轴对称图形;添加选项D中的条件,可得四边形ABCD是矩形,既是中心对称图形又是轴对称图形.故选D.
4.D ∵∠C=90°,∠B=30°,∴AB=2AC.∵BC=1,∴由勾股定理可得AB=,又题图为一个中心对称图形,点A为对称中心,∴BB'=2AB=.故选D.
5.A 选项A中的图形是轴对称图形,不是中心对称图形;选项B、C中的图形是中心对称图形,不是轴对称图形;选项D中的图形既是中心对称图形,又是轴对称图形.
6.C 菱形既是轴对称图形,又是中心对称图形.故选C.
7.C 得到的完整图形中,图①由12个弓形组成,图②由8个弓形组成,图③由6个弓形组成,图④由5个弓形组成,所以图①②③是中心对称图形,图④不是中心对称图形.故选C.
8.如图,连接BD,
∵P为平行四边形ABCD的对称中心,
∴P是平行四边形的两条对角线的交点,即BD必过点P,且BP=DP,
∵P为圆心,且过P的直线与圆相交于点M、N,∴PN=PM,又∵
∠DPN=∠BPM,
∴△PDN≌△PBM,∴BM=DN.
9.③;每个字母既可看作轴对称图形,又可看作中心对称图形
解析 ①中的字母,可看作轴对称图形的是A、E,可看作中心对称图形的是N;②中的字母,可看作轴对称图形的是K、B、X、M,其中X还可看作中心对称图形;③中的所有字母既可看作轴对称图形,又可看作中心对称图形;④中的字母,可看作轴对称图形的是H、W、D,可看作中心对称图形的是H、Z.故不同于另外三组的一组是③,这一组的特点是每个字母既可看作轴对称图形,又可看作中心对称图形.
10.161
解析 轴对称图形:线段、等腰直角三角形、等边三角形、长方形、正方形、圆,共6个,∴a=6;
中心对称图形:线段、平行四边形、长方形、正方形、圆,共5个,
∴b=5.∴a2+b3=62+53=161.
11.10
解析 如图,连接BD,与EF交于点O,∵正方形ABCD与折线DE—EF—FB构成了中心对称图形,∴OE=EF,OD=BD,∵AD=50,∴BD==50,∴OD=25.设EF=2x,则OE=x,DE=2x+25,在Rt△DOE中,x2+(2x+25)2=(25)2,解得x=5或x=-25(舍去),
∴EF=5×2=10.
12.如图,有三种画法.
同课章节目录
