1.4.2用空间向量研究距离夹角问题第2课时夹角问题课件新人教A版选择性必修第一册(共44张PPT)
文档属性
| 名称 | 1.4.2用空间向量研究距离夹角问题第2课时夹角问题课件新人教A版选择性必修第一册(共44张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-06 21:37:05 | ||
图片预览










文档简介
(共44张PPT)
第2课时 夹角问题
第一章
课标要求
1.理解两异面直线所成角与它们的方向向量之间的关系,会用向量方法求两异面直线所成角.
2.理解直线与平面所成角与直线方向向量和平面法向量夹角之间的关系,会用向量方法求直线与平面所成角.
3.理解二面角大小与两个面法向量夹角之间的关系,会用向量方法求二面角的大小.
内容索引
01
02
基础落实 必备知识全过关
重难探究 能力素养全提升
03
学以致用 随堂检测全达标
基础落实 必备知识全过关
知识点1 利用向量方法求两条异面直线所成的角
若异面直线l1,l2所成的角为θ,其方向向量分别是u,v,则cos θ=|cos|=
名师点睛
不要将两异面直线所成的角与其方向向量的夹角等同起来,因为两异面直线所成角的范围是 ,而两个向量夹角的范围是[0,π],事实上,两异面直线所成的角与其方向向量的夹角是相等或互补的关系.
过关自诊
1.判断正误.(正确的画√,错误的画×)
(1)两条异面直线所成的角与两直线的方向向量所成的角相等.( )
(2)两条异面直线所成的角一定不能为0°.( )
√
×
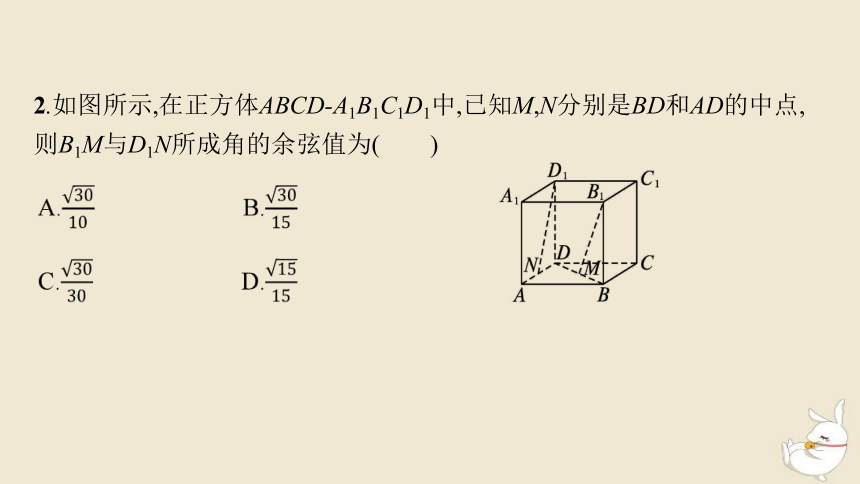
2.如图所示,在正方体ABCD-A1B1C1D1中,已知M,N分别是BD和AD的中点,则B1M与D1N所成角的余弦值为( )
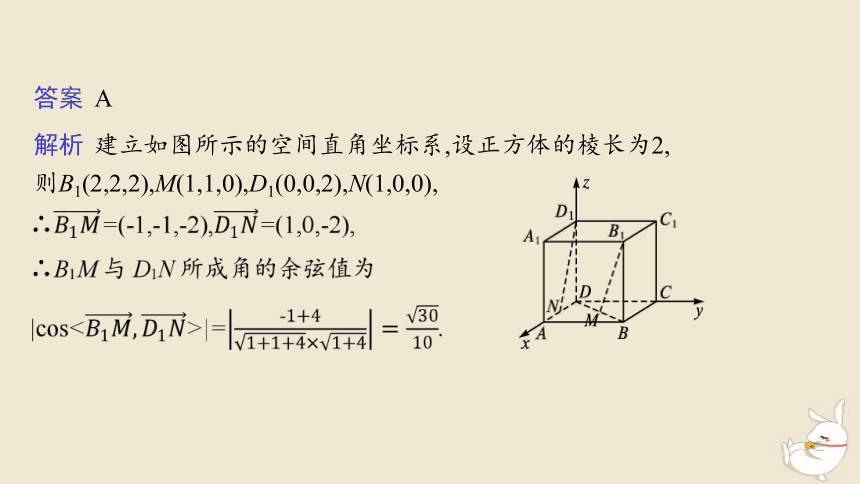
答案 A
解析 建立如图所示的空间直角坐标系,设正方体的棱长为2,
则B1(2,2,2),M(1,1,0),D1(0,0,2),N(1,0,0),
知识点2 利用向量方法求直线与平面所成的角
直线AB与平面α相交于点B,设直线AB与平面α所成的角为θ,直线AB的方向向量为u,平面α的法向量为n,则sin θ=|cos|= .
直线与平面所成的角是指这条直线与它在这个平面内的射影所成的角,其范围是
过关自诊
1.判断正误.(正确的画√,错误的画×)
(1)直线与平面所成的角等于直线与该平面法向量夹角的余角.( )
(2)直线与平面所成的角可以是钝角.( )
×
×
2.已知向量m,n分别是直线l的方向向量和平面α的法向量,若cos=- ,则l与α所成的角为( )
A.30° B.60° C.120° D.150°
答案 A
解析 设l与α所成的角为θ且θ∈[0°,90°],则sin θ=|cos|= .
∴θ=30°.
3.直线与平面所成的角和直线的方向向量与平面的法向量所成的角有怎样的关系
提示 设n为平面α的一个法向量,a为直线a的方向向量,直线a与平面α所成的角为θ,则
知识点3 利用向量方法求两个平面的夹角
1.平面α与平面β的夹角:平面α与平面β相交,形成四个二面角,我们把这四个二面角中不大于90°的二面角称为平面α与平面β的夹角.
2.若平面α,β的法向量分别是n1和n2,则平面α与平面β的夹角即为向量n1和n2的夹角或其补角,设平面α与平面β的夹角为θ,则
名师点睛
2.因为两个平面法向量的方向不确定,故若为钝角,应取其补角.
过关自诊
1.判断正误.(正确的画√,错误的画×)
(1)二面角的大小就是该二面角两个面的法向量的夹角.( )
(2)若二面角两个面的法向量的夹角为120°,则该二面角的大小等于60°或120°.( )
√
×
2.平面与平面所成的夹角与两平面的法向量所成夹角有何关系
提示 两平面的夹角是两法向量的夹角或其补角.
重难探究 能力素养全提升
探究点一
利用向量方法求两异面直线所成角
【例1】 如图所示,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,
AB=BC=AA1,∠ABC=90°,E,F分别是棱AB,BB1的中点,试求直线EF和BC1所成的角.
规律方法 1.利用空间向量求两异面直线所成角的步骤
(1)建立适当的空间直角坐标系.
(2)求出两条异面直线的方向向量的坐标.
(3)利用向量的夹角公式求出两直线方向向量的夹角.
(4)结合异面直线所成角的范围得到两异面直线所成角.
2.求两条异面直线所成的角的两个关注点
(1)余弦值非负:两条异面直线所成角的余弦值一定为非负值,而对应的方向向量的夹角可能为钝角.
(2)范围:异面直线所成角的范围是 ,故两直线方向向量夹角的余弦值为负时,应取其绝对值.
变式训练1
如图,在正四棱柱ABCD-A1B1C1D1中,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为 .
解析 以D为坐标原点,分别以DA,DC,DD1所在直线为x轴、y轴、z轴建立空间直角坐标系Dxyz(图略),设AB=1.
探究点二
利用向量方法求直线与平面所成角
【例2】 如图所示,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,
AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.
(1)证明MN∥平面PAB;
(2)求直线AN与平面PMN所成角的正弦值.
(1)证明 由已知得AM= AD=2.
如图,取BP的中点T,连接AT,TN,由N为PC的中点知TN∥BC,TN= BC=2.
又AD∥BC,故TN AM,所以四边形AMNT为平行四边形,于是MN∥AT.因为AT 平面PAB,MN 平面PAB,所以MN∥平面PAB.
(2)解 如图,取BC的中点E,连接AE.
由AB=AC得AE⊥BC,从而AE⊥AD,
规律方法 若直线l与平面α的夹角为θ,利用法向量计算θ的步骤如下
变式训练2
在棱长为1的正方体ABCD-A1B1C1D1中,E为CC1的中点,则直线A1B与平面BDE所成的角为( )
答案 B
探究点三
利用向量方法求两个平面的夹角
【例3】 如图,在正方体ABEF-DCE'F'中,M,N分别为AC,BF的中点,求平面MNA与平面MNB的夹角的余弦值.
解 设正方体棱长为1.以B为坐标原点,BA,BE,BC所在直线分别为x轴、y轴、z轴建立空间直角坐标系B-xyz(图略),则
令x=1,解得y=1,z=1,于是n1=(1,1,1).
同理可求得平面BMN的一个法向量n2=(1,-1,-1),
规律方法 利用平面的法向量求两个平面的夹角
利用向量方法求两平面夹角大小时,多采用法向量法.即求出两个面的法向量,然后通过法向量的夹角来得到两平面夹角.需注意法向量夹角范围是[0,π],而两相交平面夹角范围是 .
变式训练3
如图,在直三棱柱ABC-A1B1C1中,AA1=BC=AB=2,AB⊥BC,求平面A1B1C与平面A1CC1夹角的大小.
解 如图,以O为原点,分别以OA,OC,OB1为x轴、y轴、z轴建立空间直角坐标系.则A(2,0,0),C(0,2,0),A1(2,0,2),B1(0,0,2),C1(0,2,2),设AC的中点为M,则M(1,1,0),连接OM.
因为BM⊥AC,BM⊥CC1,所以BM⊥平面A1C1C,即
=(1,1,0)是平面A1CC1的一个法向量.
本节要点归纳
1.知识清单:
(1)异面直线所成的角;
(2)直线与平面所成的角;
(3)平面与平面所成的角.
2.方法归纳:转化化归法.
3.常见误区:容易混淆两个向量的夹角和空间角的关系.
学以致用 随堂检测全达标
1.平面α的斜线l与它在这个平面上射影l'的方向向量分别为a=(1,0,1),b=(0,1,1),则斜线l与平面α所成的角为( )
A.30° B.45° C.60° D.90°
答案 C
解析 l与α所成的角即为a与b所成的角或其补角,因为cos= ,所以=60°.l与α所成的角为60°.
2.设平面α与平面β的夹角为θ,若平面α,β的法向量分别为n1,n2,则
cos θ=( )
答案 B
3.在正方体ABCD-A1B1C1D1中,M,N分别为棱BC和棱CC1的中点,则异面直线AC和MN所成的角为( )
A.30° B.45° C.90° D.60°
答案 D
解析 以D为原点,分别以DA,DC,DD1所在直线为x轴、y轴、z轴建立空间直角坐标系,
设正方体ABCD-A1B1C1D1中棱长为2,∵M,N分别为棱BC和棱CC1的中点,
又θ是锐角,∴θ=60°.
∴异面直线AC和MN所成的角为60°,故选D.
4.正方体ABCD-A1B1C1D1中,BB1与平面ACD1所成角的正弦值为 .
解析 设正方体的棱长为1,建立空间直角坐标系如图.
则D(0,0,0),B(1,1,0),B1(1,1,1).
5.如图,在四棱锥P-ABCD中,PB⊥底面ABCD,CD⊥PD,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3.点E在棱PA上,且PE=2EA.求平面ABE与平面DBE夹角的余弦值.
解 以B为原点,以直线BC,BA,BP分别为x轴、y轴、z轴建立如图所示的空间直角坐标系,则P(0,0,3),A(0,3,0),D(3,3,0).
设平面EBD的一个法向量为n1=(x,y,z),
第2课时 夹角问题
第一章
课标要求
1.理解两异面直线所成角与它们的方向向量之间的关系,会用向量方法求两异面直线所成角.
2.理解直线与平面所成角与直线方向向量和平面法向量夹角之间的关系,会用向量方法求直线与平面所成角.
3.理解二面角大小与两个面法向量夹角之间的关系,会用向量方法求二面角的大小.
内容索引
01
02
基础落实 必备知识全过关
重难探究 能力素养全提升
03
学以致用 随堂检测全达标
基础落实 必备知识全过关
知识点1 利用向量方法求两条异面直线所成的角
若异面直线l1,l2所成的角为θ,其方向向量分别是u,v,则cos θ=|cos
名师点睛
不要将两异面直线所成的角与其方向向量的夹角等同起来,因为两异面直线所成角的范围是 ,而两个向量夹角的范围是[0,π],事实上,两异面直线所成的角与其方向向量的夹角是相等或互补的关系.
过关自诊
1.判断正误.(正确的画√,错误的画×)
(1)两条异面直线所成的角与两直线的方向向量所成的角相等.( )
(2)两条异面直线所成的角一定不能为0°.( )
√
×
2.如图所示,在正方体ABCD-A1B1C1D1中,已知M,N分别是BD和AD的中点,则B1M与D1N所成角的余弦值为( )
答案 A
解析 建立如图所示的空间直角坐标系,设正方体的棱长为2,
则B1(2,2,2),M(1,1,0),D1(0,0,2),N(1,0,0),
知识点2 利用向量方法求直线与平面所成的角
直线AB与平面α相交于点B,设直线AB与平面α所成的角为θ,直线AB的方向向量为u,平面α的法向量为n,则sin θ=|cos
直线与平面所成的角是指这条直线与它在这个平面内的射影所成的角,其范围是
过关自诊
1.判断正误.(正确的画√,错误的画×)
(1)直线与平面所成的角等于直线与该平面法向量夹角的余角.( )
(2)直线与平面所成的角可以是钝角.( )
×
×
2.已知向量m,n分别是直线l的方向向量和平面α的法向量,若cos
A.30° B.60° C.120° D.150°
答案 A
解析 设l与α所成的角为θ且θ∈[0°,90°],则sin θ=|cos
∴θ=30°.
3.直线与平面所成的角和直线的方向向量与平面的法向量所成的角有怎样的关系
提示 设n为平面α的一个法向量,a为直线a的方向向量,直线a与平面α所成的角为θ,则
知识点3 利用向量方法求两个平面的夹角
1.平面α与平面β的夹角:平面α与平面β相交,形成四个二面角,我们把这四个二面角中不大于90°的二面角称为平面α与平面β的夹角.
2.若平面α,β的法向量分别是n1和n2,则平面α与平面β的夹角即为向量n1和n2的夹角或其补角,设平面α与平面β的夹角为θ,则
名师点睛
2.因为两个平面法向量的方向不确定,故若
过关自诊
1.判断正误.(正确的画√,错误的画×)
(1)二面角的大小就是该二面角两个面的法向量的夹角.( )
(2)若二面角两个面的法向量的夹角为120°,则该二面角的大小等于60°或120°.( )
√
×
2.平面与平面所成的夹角与两平面的法向量所成夹角有何关系
提示 两平面的夹角是两法向量的夹角或其补角.
重难探究 能力素养全提升
探究点一
利用向量方法求两异面直线所成角
【例1】 如图所示,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,
AB=BC=AA1,∠ABC=90°,E,F分别是棱AB,BB1的中点,试求直线EF和BC1所成的角.
规律方法 1.利用空间向量求两异面直线所成角的步骤
(1)建立适当的空间直角坐标系.
(2)求出两条异面直线的方向向量的坐标.
(3)利用向量的夹角公式求出两直线方向向量的夹角.
(4)结合异面直线所成角的范围得到两异面直线所成角.
2.求两条异面直线所成的角的两个关注点
(1)余弦值非负:两条异面直线所成角的余弦值一定为非负值,而对应的方向向量的夹角可能为钝角.
(2)范围:异面直线所成角的范围是 ,故两直线方向向量夹角的余弦值为负时,应取其绝对值.
变式训练1
如图,在正四棱柱ABCD-A1B1C1D1中,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为 .
解析 以D为坐标原点,分别以DA,DC,DD1所在直线为x轴、y轴、z轴建立空间直角坐标系Dxyz(图略),设AB=1.
探究点二
利用向量方法求直线与平面所成角
【例2】 如图所示,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,
AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.
(1)证明MN∥平面PAB;
(2)求直线AN与平面PMN所成角的正弦值.
(1)证明 由已知得AM= AD=2.
如图,取BP的中点T,连接AT,TN,由N为PC的中点知TN∥BC,TN= BC=2.
又AD∥BC,故TN AM,所以四边形AMNT为平行四边形,于是MN∥AT.因为AT 平面PAB,MN 平面PAB,所以MN∥平面PAB.
(2)解 如图,取BC的中点E,连接AE.
由AB=AC得AE⊥BC,从而AE⊥AD,
规律方法 若直线l与平面α的夹角为θ,利用法向量计算θ的步骤如下
变式训练2
在棱长为1的正方体ABCD-A1B1C1D1中,E为CC1的中点,则直线A1B与平面BDE所成的角为( )
答案 B
探究点三
利用向量方法求两个平面的夹角
【例3】 如图,在正方体ABEF-DCE'F'中,M,N分别为AC,BF的中点,求平面MNA与平面MNB的夹角的余弦值.
解 设正方体棱长为1.以B为坐标原点,BA,BE,BC所在直线分别为x轴、y轴、z轴建立空间直角坐标系B-xyz(图略),则
令x=1,解得y=1,z=1,于是n1=(1,1,1).
同理可求得平面BMN的一个法向量n2=(1,-1,-1),
规律方法 利用平面的法向量求两个平面的夹角
利用向量方法求两平面夹角大小时,多采用法向量法.即求出两个面的法向量,然后通过法向量的夹角来得到两平面夹角.需注意法向量夹角范围是[0,π],而两相交平面夹角范围是 .
变式训练3
如图,在直三棱柱ABC-A1B1C1中,AA1=BC=AB=2,AB⊥BC,求平面A1B1C与平面A1CC1夹角的大小.
解 如图,以O为原点,分别以OA,OC,OB1为x轴、y轴、z轴建立空间直角坐标系.则A(2,0,0),C(0,2,0),A1(2,0,2),B1(0,0,2),C1(0,2,2),设AC的中点为M,则M(1,1,0),连接OM.
因为BM⊥AC,BM⊥CC1,所以BM⊥平面A1C1C,即
=(1,1,0)是平面A1CC1的一个法向量.
本节要点归纳
1.知识清单:
(1)异面直线所成的角;
(2)直线与平面所成的角;
(3)平面与平面所成的角.
2.方法归纳:转化化归法.
3.常见误区:容易混淆两个向量的夹角和空间角的关系.
学以致用 随堂检测全达标
1.平面α的斜线l与它在这个平面上射影l'的方向向量分别为a=(1,0,1),b=(0,1,1),则斜线l与平面α所成的角为( )
A.30° B.45° C.60° D.90°
答案 C
解析 l与α所成的角即为a与b所成的角或其补角,因为cos
2.设平面α与平面β的夹角为θ,若平面α,β的法向量分别为n1,n2,则
cos θ=( )
答案 B
3.在正方体ABCD-A1B1C1D1中,M,N分别为棱BC和棱CC1的中点,则异面直线AC和MN所成的角为( )
A.30° B.45° C.90° D.60°
答案 D
解析 以D为原点,分别以DA,DC,DD1所在直线为x轴、y轴、z轴建立空间直角坐标系,
设正方体ABCD-A1B1C1D1中棱长为2,∵M,N分别为棱BC和棱CC1的中点,
又θ是锐角,∴θ=60°.
∴异面直线AC和MN所成的角为60°,故选D.
4.正方体ABCD-A1B1C1D1中,BB1与平面ACD1所成角的正弦值为 .
解析 设正方体的棱长为1,建立空间直角坐标系如图.
则D(0,0,0),B(1,1,0),B1(1,1,1).
5.如图,在四棱锥P-ABCD中,PB⊥底面ABCD,CD⊥PD,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3.点E在棱PA上,且PE=2EA.求平面ABE与平面DBE夹角的余弦值.
解 以B为原点,以直线BC,BA,BP分别为x轴、y轴、z轴建立如图所示的空间直角坐标系,则P(0,0,3),A(0,3,0),D(3,3,0).
设平面EBD的一个法向量为n1=(x,y,z),
