1.1.2菱形的性质与判定 课件(共26张PPT)
文档属性
| 名称 | 1.1.2菱形的性质与判定 课件(共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 846.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-16 14:59:54 | ||
图片预览



文档简介
(共26张PPT)
北师大版九年级上册
第一章
特殊平行四边形
1.1 菱形的性质与判定(二)
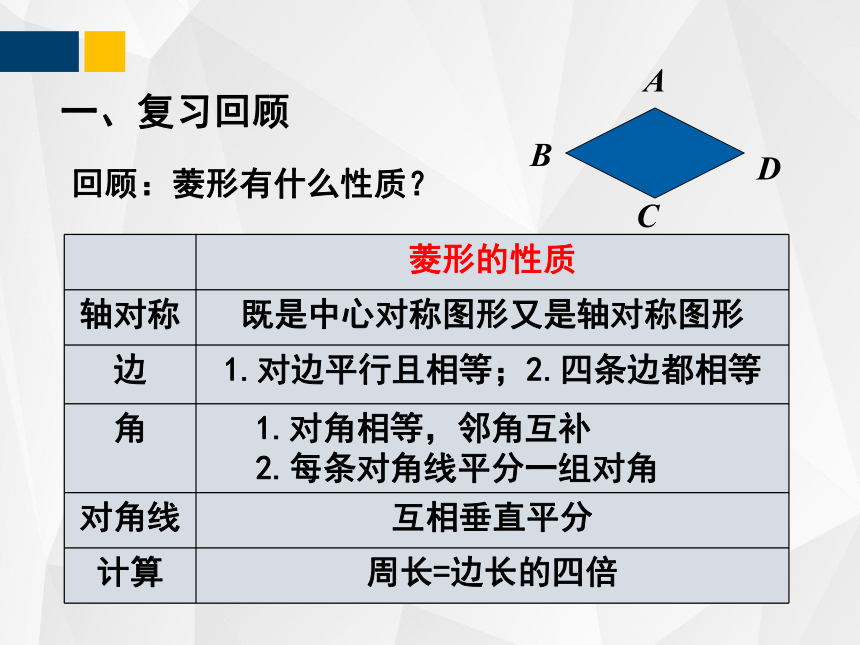
一、复习回顾
回顾:菱形有什么性质?
菱形的性质
轴对称 既是中心对称图形又是轴对称图形
边 1.对边平行且相等;2.四条边都相等
角 1.对角相等,邻角互补
2.每条对角线平分一组对角
对角线 互相垂直平分
计算 周长=边长的四倍
A
D
C
B
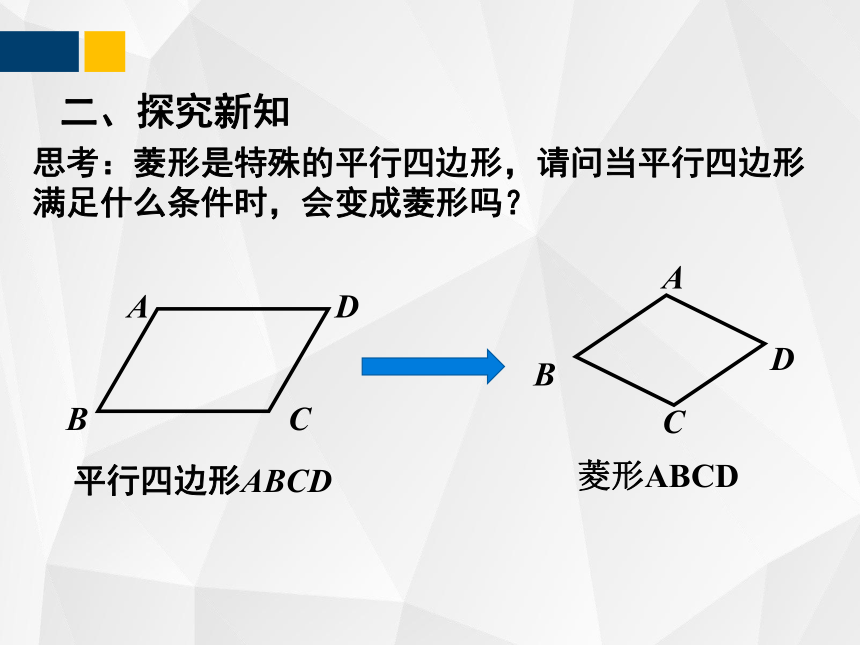
二、探究新知
思考:菱形是特殊的平行四边形,请问当平行四边形满足什么条件时,会变成菱形吗?
A
B
C
D
平行四边形ABCD
A
B
C
D
菱形ABCD
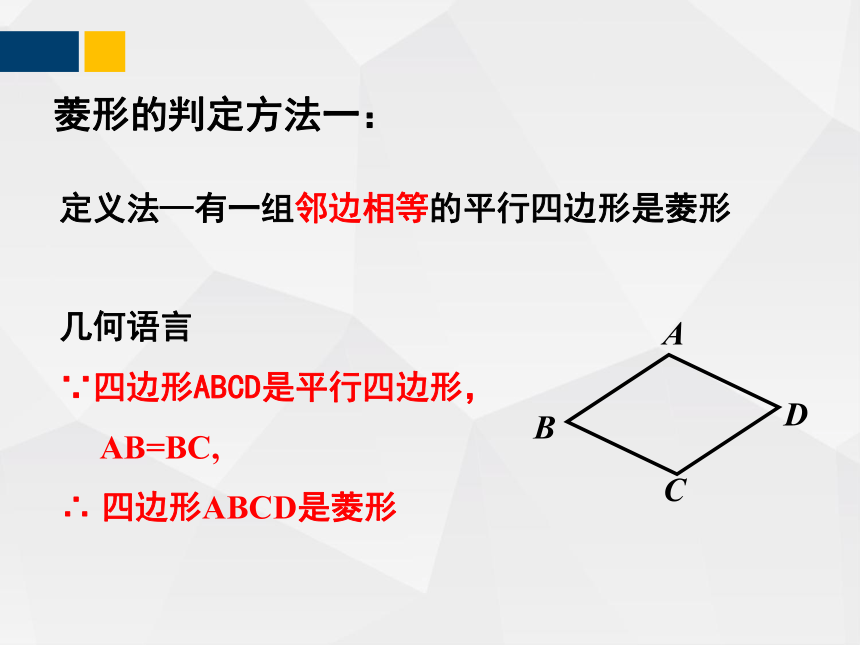
定义法—有一组邻边相等的平行四边形是菱形
几何语言
∵四边形ABCD是平行四边形,
AB=BC,
∴ 四边形ABCD是菱形
A
B
C
D
菱形的判定方法一:
在一个平行四边形中,绕着对角线的中点,转动两条对角线,当两条对角线转动到什么位置时,这个平行四边形变成菱形
猜想:
对角线互相垂直的平行四边形是菱形
探究活动一
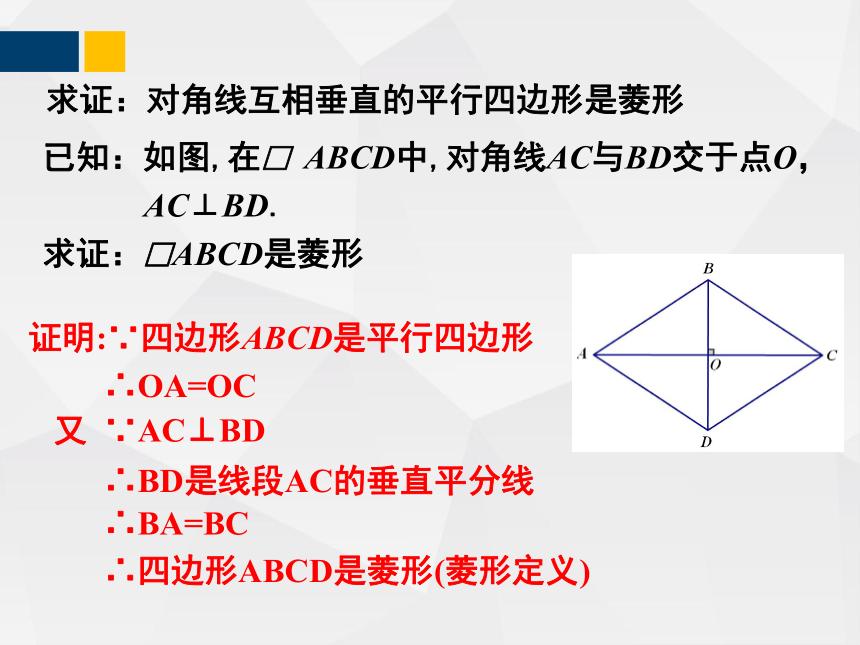
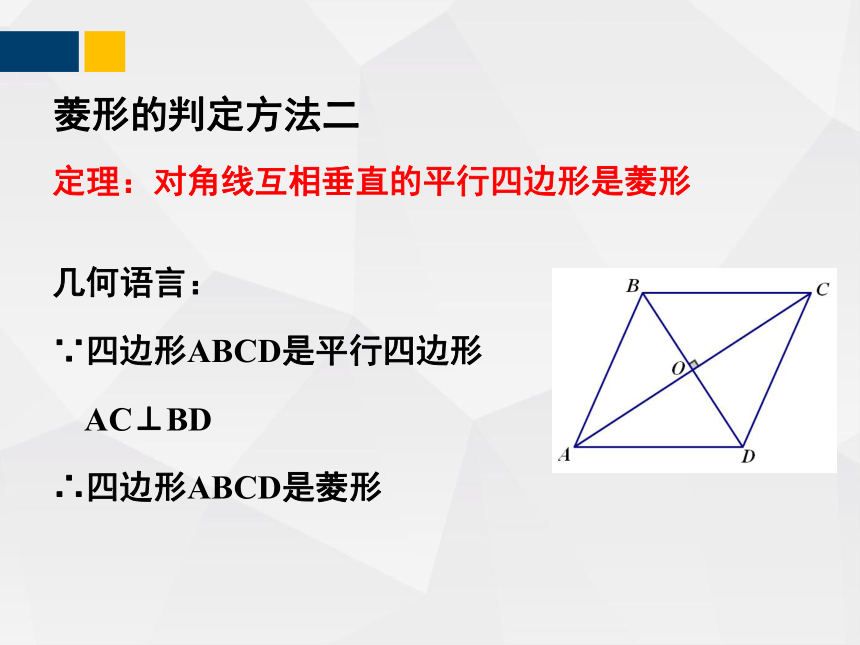
求证:对角线互相垂直的平行四边形是菱形
已知:如图,在□ ABCD中,对角线AC与BD交于点O,
AC⊥BD.
求证:□ABCD是菱形
证明:∵四边形ABCD是平行四边形
∴OA=OC
又 ∵AC⊥BD
∴BD是线段AC的垂直平分线
∴BA=BC
∴四边形ABCD是菱形(菱形定义)
定理:对角线互相垂直的平行四边形是菱形
几何语言:
∵四边形ABCD是平行四边形
AC⊥BD
∴四边形ABCD是菱形
菱形的判定方法二
探究活动二
请准备好四根长度相等的木条(或笔芯),首尾相接摆放在一起。观察所摆放的四边形是什么样的四边形?由此你能得到什么结论?
猜想:四条边相等的四边形是菱形
A
B
C
D
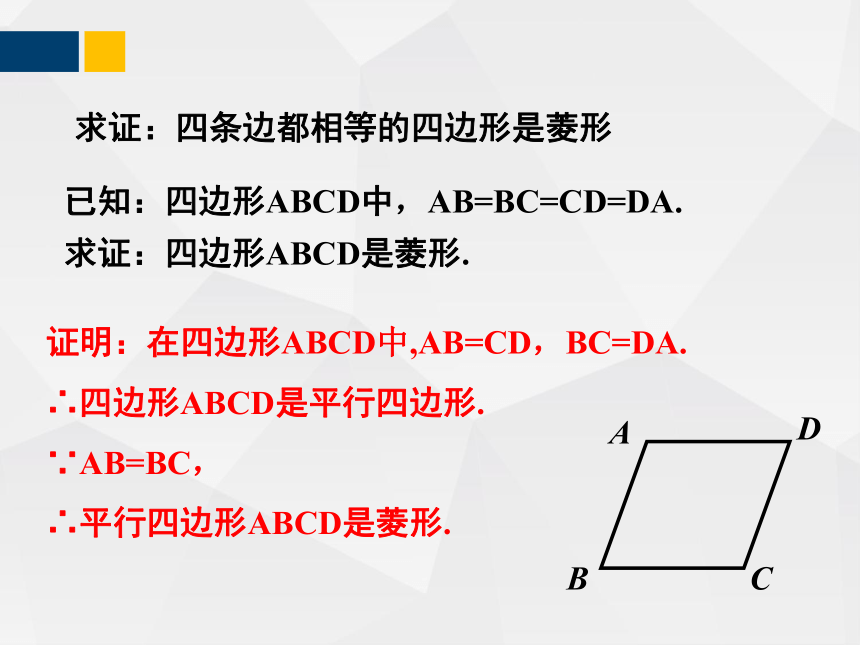
证明:在四边形ABCD中,AB=CD,BC=DA.
∴四边形ABCD是平行四边形.
∵AB=BC,
∴平行四边形ABCD是菱形.
求证:四条边都相等的四边形是菱形
已知:四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形.
菱形的判定方法三
定理:四条边相等的四边形是菱形
几何语言:
∵四边形ABCD中
AB=BC=CD=DA
∴四边形ABCD是菱形.
A
B
C
D
1. 已知线段AC,你能用尺规作图的方法作一个以AC 为对角线的菱形ABCD吗?
议一议:
小皓同学的做法:
分别以A,C为圆心,以大于AC的长为半径作弧,两条弧分别相交于点B,D,依次连接A,B,C,D,则四边形ABCD为菱形
你能说说这样做的道理吗?
四条边相等的四边形是菱形
2.你能用折纸方法得到一个菱形吗?动手试试
议一议:
小鹏同学的做法:先将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,将纸展开,就得到一个菱形
你能说说这样做的道理吗?
四条边相等的四边形是菱形
总结归纳
菱形的判定方法 几何语言
定义法 有一组邻边相等的平行四边形是菱形 ∵□ABCD, AB=BC,
∴ 四边形ABCD是菱形
定理 对角线互相垂直的平行四边形是菱形 ∵□ABCD, AC⊥BD,
∴ 四边形ABCD是菱形
定理 四条边相等的四边形是菱形 ∵四边形ABCD中,
AB=BC=CD=DA
∴四边形ABCD是菱形.
A
B
C
D
证明:在△AOB中.
∵AB= , OA=2,OB=1.
∴AB2=AO2+OB2.
∴ △AOB是直角三角形, ∠AOB是直角.
∴AC⊥BD.
∴ □ABCD是菱形 (对角线垂直的平行四边形是菱形).
例1:已知:如图,在□ABCD中,对角线AC与BD相交于点O,AB= ,OA=2,OB=1. 求证:□ABCD是菱形.
A
B
C
O
D
三、典提精析
例2:已知:如图,在□ ABCD中,对角线BD平分∠ABC,求证:四边形BCFD是菱形
B
A
D
C
证明:∵四边形ABCD是平行四边形
∴AB∥CD
∴ ∠ ABD= ∠BDC
∵ BD平分∠ABC
∴ ∠ ABD= ∠CBD
∴ ∠BDC= ∠CBD
∴AB=AD
∴四边形ABCD是菱形.
三、典提精析
四、巩固练习
1. 如图,要使□ ABCD成为菱形,则需添加的一个条件是( )
AC=AD
B. BA=BC
C. ∠ABC=90°
D. AC=BD
B
四、巩固练习
2.如图,四边形ABCD的对角线AC,BD互相垂直,则下列条件能判定四边形ABCD为菱形的是( )
A.BA=BC
B.AC,BD互相平分
C.AC=BD
D.AB∥CD
B
四、巩固练习
3.下列条件中,不能判定四边形ABCD为菱形的是 ( )
A. AC⊥BD ,AC与BD互相平分
B. AB=BC=CD=DA
C. AB=BC,AD=CD,AC ⊥BD
D. AB=CD,AD=BC,AC ⊥BD
A
B
C
O
D
C
4.如图,在△ABC中,AB= AC ,点D,E,F分别是BC,AB,AC的中点,连接DE, DF.
求证:四边形AEDF是菱形.
四、巩固练习
C
A
B
D
E
F
证明:∵点D,E分别BC,AB的中点,
∴DE = AC,DE ∥ AF
同理, DF = AB,DF ∥ AE
∴四边形AEDF是平行四边形
∵ AC=AB
∴ DE = DF
∴四边形AEDF是菱形.
四、巩固练习
C
A
B
D
E
F
C
A
B
H
E
F
证明:∵ AB=AC, AH⊥BC
∴BH= HC
∵ FH=EH
∴四边形EBFC是平行四边形
又∵ AH⊥BC
∴四边形EBFC是菱形.
5.如图,在等腰△ABC中,AB= AC ,AH⊥BC,点E是AH上一点,延长AH至点F,使FH=EH.
求证:四边形EBFC是菱形.
四、巩固练习
6.如图,在四边形ABCD中,∠A=90°,AD∥BC,BE⊥CD于点E,交AD的延长线于点F,连接CF,DC=2AD,AB=EB.
求证:(1)AD=DE;
(2)四边形BCFD是菱形.
四、巩固练习
证明:(1)∵∠A=90°,BE⊥CD
在Rt△BDA与Rt△BDE中,
AB=EB, BD=BD,
∴Rt△BDA≌Rt△BDE(HL)
∴AD=DE.
(2) ∵AD=DE,DC=DE+EC=2AD=2DE,∴DE=EC.
又∵AD∥BC, ∠DFB= ∠FBC, ∠FDC= ∠DCB
∴△DEF≌△CEB(AAS)
∴DF=BC.
∴四边形BCFD为平行四边形.
又∵BE⊥CD,
∴四边形BCFD是菱形.
菱形的判定方法 几何语言
定义法 有一组邻边相等的平行四边形是菱形 ∵□ABCD, AB=BC,
∴ 四边形ABCD是菱形
定理 对角线互相垂直的平行四边形是菱形 ∵□ABCD, AC⊥BD,
∴ 四边形ABCD是菱形
定理 四条边相等的四边形是菱形 ∵四边形ABCD中,
AB=BC=CD=DA
∴四边形ABCD是菱形.
A
B
C
D
五、课堂小结
六、布置作业
课本P7 习题1.2 第1,2,3题
谢谢聆听
北师大版九年级上册
第一章
特殊平行四边形
1.1 菱形的性质与判定(二)
一、复习回顾
回顾:菱形有什么性质?
菱形的性质
轴对称 既是中心对称图形又是轴对称图形
边 1.对边平行且相等;2.四条边都相等
角 1.对角相等,邻角互补
2.每条对角线平分一组对角
对角线 互相垂直平分
计算 周长=边长的四倍
A
D
C
B
二、探究新知
思考:菱形是特殊的平行四边形,请问当平行四边形满足什么条件时,会变成菱形吗?
A
B
C
D
平行四边形ABCD
A
B
C
D
菱形ABCD
定义法—有一组邻边相等的平行四边形是菱形
几何语言
∵四边形ABCD是平行四边形,
AB=BC,
∴ 四边形ABCD是菱形
A
B
C
D
菱形的判定方法一:
在一个平行四边形中,绕着对角线的中点,转动两条对角线,当两条对角线转动到什么位置时,这个平行四边形变成菱形
猜想:
对角线互相垂直的平行四边形是菱形
探究活动一
求证:对角线互相垂直的平行四边形是菱形
已知:如图,在□ ABCD中,对角线AC与BD交于点O,
AC⊥BD.
求证:□ABCD是菱形
证明:∵四边形ABCD是平行四边形
∴OA=OC
又 ∵AC⊥BD
∴BD是线段AC的垂直平分线
∴BA=BC
∴四边形ABCD是菱形(菱形定义)
定理:对角线互相垂直的平行四边形是菱形
几何语言:
∵四边形ABCD是平行四边形
AC⊥BD
∴四边形ABCD是菱形
菱形的判定方法二
探究活动二
请准备好四根长度相等的木条(或笔芯),首尾相接摆放在一起。观察所摆放的四边形是什么样的四边形?由此你能得到什么结论?
猜想:四条边相等的四边形是菱形
A
B
C
D
证明:在四边形ABCD中,AB=CD,BC=DA.
∴四边形ABCD是平行四边形.
∵AB=BC,
∴平行四边形ABCD是菱形.
求证:四条边都相等的四边形是菱形
已知:四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形.
菱形的判定方法三
定理:四条边相等的四边形是菱形
几何语言:
∵四边形ABCD中
AB=BC=CD=DA
∴四边形ABCD是菱形.
A
B
C
D
1. 已知线段AC,你能用尺规作图的方法作一个以AC 为对角线的菱形ABCD吗?
议一议:
小皓同学的做法:
分别以A,C为圆心,以大于AC的长为半径作弧,两条弧分别相交于点B,D,依次连接A,B,C,D,则四边形ABCD为菱形
你能说说这样做的道理吗?
四条边相等的四边形是菱形
2.你能用折纸方法得到一个菱形吗?动手试试
议一议:
小鹏同学的做法:先将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,将纸展开,就得到一个菱形
你能说说这样做的道理吗?
四条边相等的四边形是菱形
总结归纳
菱形的判定方法 几何语言
定义法 有一组邻边相等的平行四边形是菱形 ∵□ABCD, AB=BC,
∴ 四边形ABCD是菱形
定理 对角线互相垂直的平行四边形是菱形 ∵□ABCD, AC⊥BD,
∴ 四边形ABCD是菱形
定理 四条边相等的四边形是菱形 ∵四边形ABCD中,
AB=BC=CD=DA
∴四边形ABCD是菱形.
A
B
C
D
证明:在△AOB中.
∵AB= , OA=2,OB=1.
∴AB2=AO2+OB2.
∴ △AOB是直角三角形, ∠AOB是直角.
∴AC⊥BD.
∴ □ABCD是菱形 (对角线垂直的平行四边形是菱形).
例1:已知:如图,在□ABCD中,对角线AC与BD相交于点O,AB= ,OA=2,OB=1. 求证:□ABCD是菱形.
A
B
C
O
D
三、典提精析
例2:已知:如图,在□ ABCD中,对角线BD平分∠ABC,求证:四边形BCFD是菱形
B
A
D
C
证明:∵四边形ABCD是平行四边形
∴AB∥CD
∴ ∠ ABD= ∠BDC
∵ BD平分∠ABC
∴ ∠ ABD= ∠CBD
∴ ∠BDC= ∠CBD
∴AB=AD
∴四边形ABCD是菱形.
三、典提精析
四、巩固练习
1. 如图,要使□ ABCD成为菱形,则需添加的一个条件是( )
AC=AD
B. BA=BC
C. ∠ABC=90°
D. AC=BD
B
四、巩固练习
2.如图,四边形ABCD的对角线AC,BD互相垂直,则下列条件能判定四边形ABCD为菱形的是( )
A.BA=BC
B.AC,BD互相平分
C.AC=BD
D.AB∥CD
B
四、巩固练习
3.下列条件中,不能判定四边形ABCD为菱形的是 ( )
A. AC⊥BD ,AC与BD互相平分
B. AB=BC=CD=DA
C. AB=BC,AD=CD,AC ⊥BD
D. AB=CD,AD=BC,AC ⊥BD
A
B
C
O
D
C
4.如图,在△ABC中,AB= AC ,点D,E,F分别是BC,AB,AC的中点,连接DE, DF.
求证:四边形AEDF是菱形.
四、巩固练习
C
A
B
D
E
F
证明:∵点D,E分别BC,AB的中点,
∴DE = AC,DE ∥ AF
同理, DF = AB,DF ∥ AE
∴四边形AEDF是平行四边形
∵ AC=AB
∴ DE = DF
∴四边形AEDF是菱形.
四、巩固练习
C
A
B
D
E
F
C
A
B
H
E
F
证明:∵ AB=AC, AH⊥BC
∴BH= HC
∵ FH=EH
∴四边形EBFC是平行四边形
又∵ AH⊥BC
∴四边形EBFC是菱形.
5.如图,在等腰△ABC中,AB= AC ,AH⊥BC,点E是AH上一点,延长AH至点F,使FH=EH.
求证:四边形EBFC是菱形.
四、巩固练习
6.如图,在四边形ABCD中,∠A=90°,AD∥BC,BE⊥CD于点E,交AD的延长线于点F,连接CF,DC=2AD,AB=EB.
求证:(1)AD=DE;
(2)四边形BCFD是菱形.
四、巩固练习
证明:(1)∵∠A=90°,BE⊥CD
在Rt△BDA与Rt△BDE中,
AB=EB, BD=BD,
∴Rt△BDA≌Rt△BDE(HL)
∴AD=DE.
(2) ∵AD=DE,DC=DE+EC=2AD=2DE,∴DE=EC.
又∵AD∥BC, ∠DFB= ∠FBC, ∠FDC= ∠DCB
∴△DEF≌△CEB(AAS)
∴DF=BC.
∴四边形BCFD为平行四边形.
又∵BE⊥CD,
∴四边形BCFD是菱形.
菱形的判定方法 几何语言
定义法 有一组邻边相等的平行四边形是菱形 ∵□ABCD, AB=BC,
∴ 四边形ABCD是菱形
定理 对角线互相垂直的平行四边形是菱形 ∵□ABCD, AC⊥BD,
∴ 四边形ABCD是菱形
定理 四条边相等的四边形是菱形 ∵四边形ABCD中,
AB=BC=CD=DA
∴四边形ABCD是菱形.
A
B
C
D
五、课堂小结
六、布置作业
课本P7 习题1.2 第1,2,3题
谢谢聆听
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
