1.2.1矩形的性质与判定 课件(共25张PPT)
文档属性
| 名称 | 1.2.1矩形的性质与判定 课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 677.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-16 14:59:54 | ||
图片预览




文档简介
(共25张PPT)
北师大版九年级上册
第一章
特殊平行四边形
1.2 矩形的性质与判定(一)
一、情景导入
思考:这种平行四边形特殊在哪里?
图片中有你熟悉的图形吗?
定义:有一个角是直角的平行四边形叫做矩形
几何语言:
∵四边形ABCD是平行四边形
∠A=90°( 或∠B=90° )
∴四边形ABCD是矩形
学习概念
★矩形是特殊的平行四边形
A
D
C
B
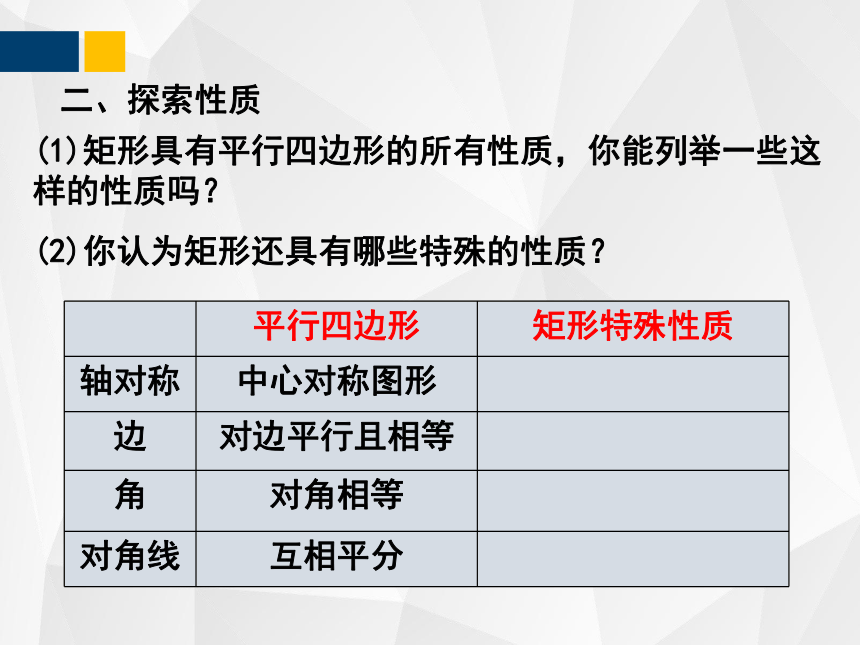
(1)矩形具有平行四边形的所有性质,你能列举一些这样的性质吗?
(2)你认为矩形还具有哪些特殊的性质?
平行四边形 矩形特殊性质
轴对称 中心对称图形
边 对边平行且相等
角 对角相等
对角线 互相平分
二、探索性质
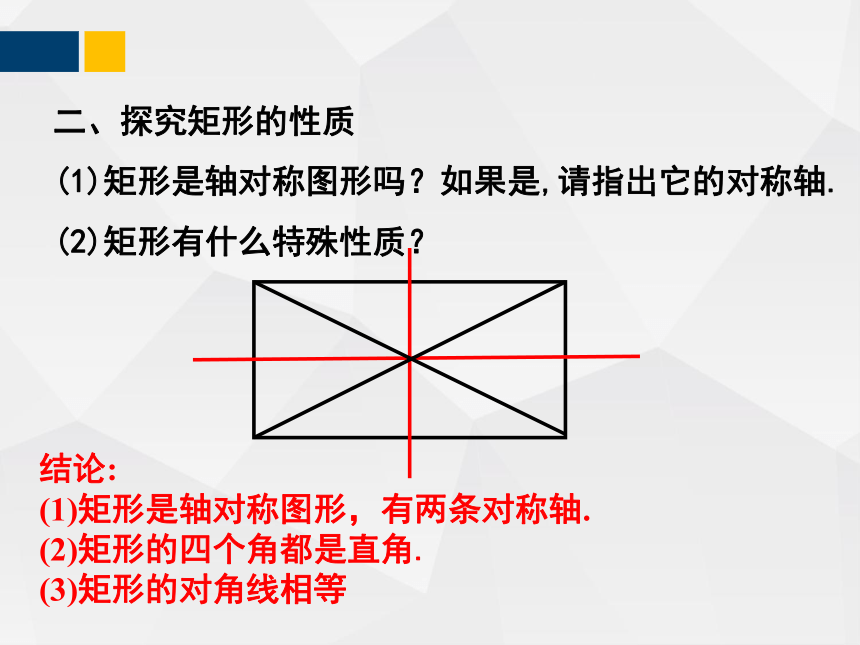
二、探究矩形的性质
(1)矩形是轴对称图形吗?如果是,请指出它的对称轴.
(2)矩形有什么特殊性质?
结论:
(1)矩形是轴对称图形,有两条对称轴.
(2)矩形的四个角都是直角.
(3)矩形的对角线相等
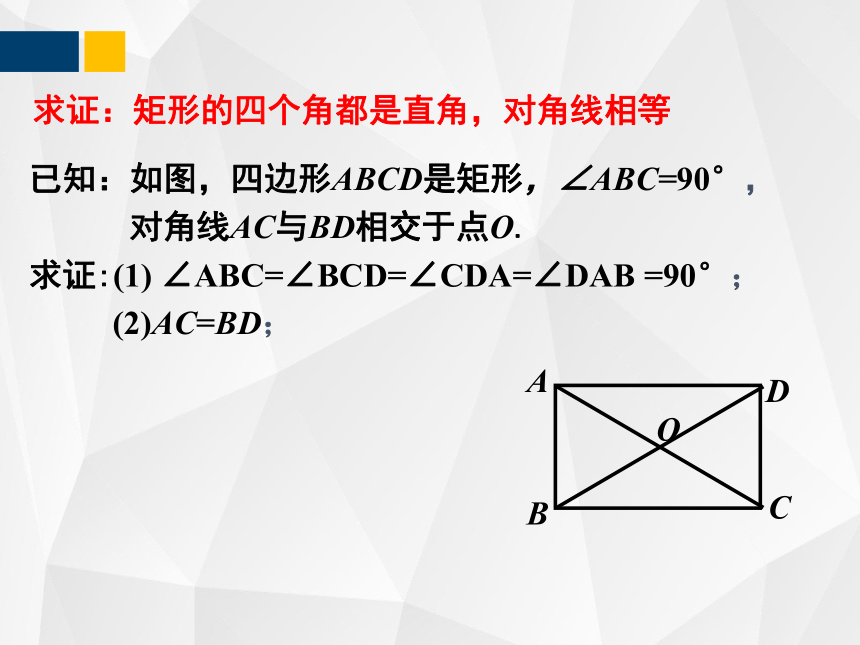
已知:如图,四边形ABCD是矩形,∠ABC=90°,
对角线AC与BD相交于点O.
求证:(1) ∠ABC=∠BCD=∠CDA=∠DAB =90°;
(2)AC=BD;
求证:矩形的四个角都是直角,对角线相等
A
D
C
B
O
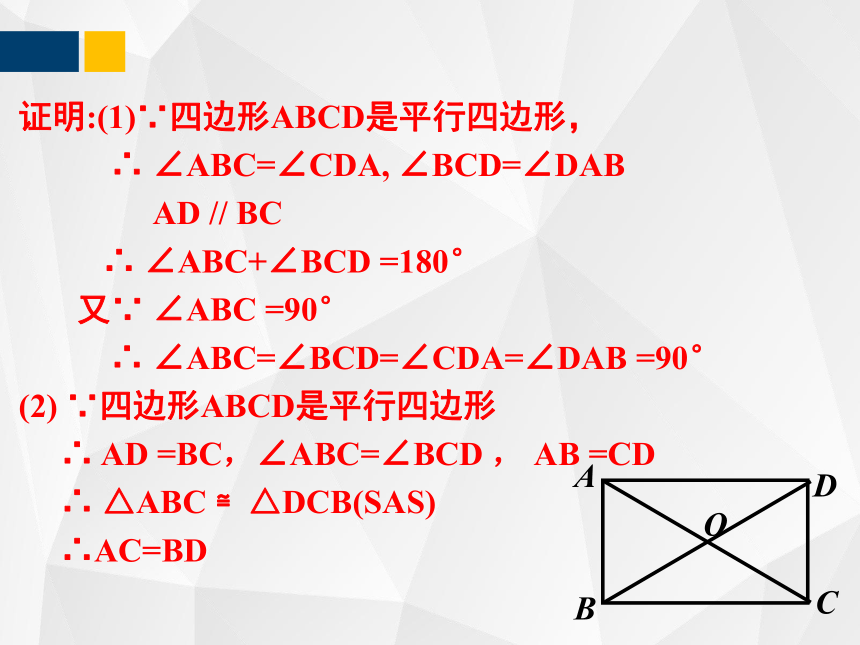
证明:(1)∵四边形ABCD是平行四边形,
∴ ∠ABC=∠CDA, ∠BCD=∠DAB
AD // BC
∴ ∠ABC+∠BCD =180°
又∵ ∠ABC =90°
∴ ∠ABC=∠BCD=∠CDA=∠DAB =90°
(2) ∵四边形ABCD是平行四边形
∴ AD =BC,∠ABC=∠BCD , AB =CD
∴ △ABC ≌△DCB(SAS)
∴AC=BD
A
D
C
B
O
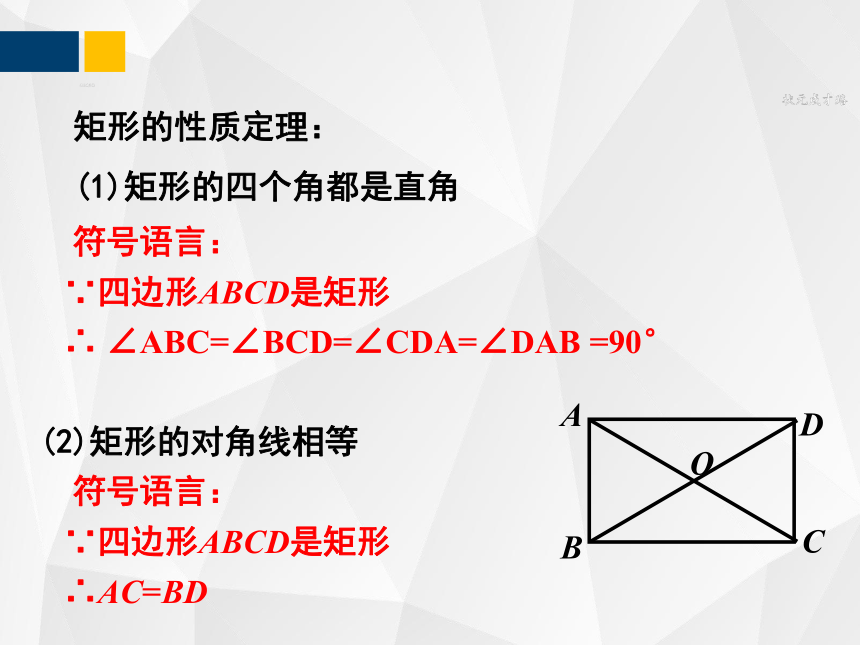
矩形的性质定理:
(1)矩形的四个角都是直角
符号语言:
∵四边形ABCD是矩形
∴ ∠ABC=∠BCD=∠CDA=∠DAB =90°
(2)矩形的对角线相等
符号语言:
∵四边形ABCD是矩形
∴AC=BD
A
D
C
B
O
平行四边形 矩形的特殊性质
轴对称 中心对称图形 轴对称图形
边 对边平行且相等 /
角 对角相等 四个角都是直角
对角线 互相平分 相等
归纳总结
矩形是特殊的平行四边形,除具有平行四边形的所有性质外,还有平行四边形所没有的特殊性质.
如图,矩形ABCD的对角线AC与BD交于点O,思考:
(1)BO是Rt△ABC中斜边AC上什么特殊线段
(2)BO与AC有什么大小关系
D
B
C
A
O
探究直角三角形的性质
猜想:BO 是Rt△ABC中斜边AC上的中线,
且BO等于AC的一半
如图,矩形ABCD的对角线AC与BD交于点O,
求证:(1)BO是Rt△ABC斜边AC上的中线;
(2) BO= AC
D
B
C
A
O
证明:(1) ∵四边形ABCD是矩形
∴O是AC的中点
∴ BO是Rt△ABC斜边AC上的中线
(2) ∵四边形ABCD是矩形
∴AC=BD,OB= BD
∴ OB= AC
总结归纳:
直角三角形斜边上中线的性质
直角三角形斜边上的中线等于斜边的一半
符号语言:
∵ Rt△ABC,O是AC的中点
∴ BO= AC
A
B
C
O
例1:如图,在矩形ABCD中,两条对角线相交于点O,
∠AOD=120°,AB=2.5 ,求矩形对角线的长.
A
B
C
D
O
二、典例精析
证明:∵四边形ABCD是矩形
∴ ∠BAD=90°, AC=BD
OA= AC,OD= BD,
∴ OA= OD
∵∠AOD=120°
∴ ∠OAD= ∠ODA=30 °
在Rt△ABD中,
BD=2AB=2×2.5=5
如图,在矩形ABCD中,两条对角线AC,BD相交于点O,∠ACD=30°,AD=2.
(1)判断△AOD的形状;
(2)求对角线AC的长.
变式练习
解:(1)∵四边形ABCD为矩形,
∴∠ADC=90°,OA=OD=OC=OB.
∵∠ACD=30°,
∴∠DAC=90°- 30°=60°.
而∵ OA=OD
∴△AOD为等边三角形.
(2)∵△AOD为等边三角形,∴AO=AD=2.
∴AC=2AO=4.
四、巩固练习
1.如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=2,则矩形的边长BC的长是( )
A.2 B.4 C.2 D.4
C
2. 如图,在 ABCD中,对角线AC,BD相交于点O,OA=OB,若AD=4,∠AOD=60°,则AB的长( )
A. 4 B. 2 C. 8 D. 8
A
四、巩固练习
四、巩固练习
3. 如图,矩形ABCD的对角线AC,BD交于点O,∠AOD=60°,AB=2 ,AE⊥BD于点E,则OE的长为________.
1
4.如图,在矩形ABCD中,O是对角线AC的中点,OM∥AB交AD于点M,若OM=3,BC=10,则OB的长为( )
A. 5 B. 4 C. D.
D
2
___
四、巩固练习
5.已知:如图,在矩形ABCD中,对角线AC,BD相交于点O,过点D作DE∥AC交BC延长线于点E.
求证:BD=DE.
证明:在矩形ABCD中,
∴AC=BD,AD∥BC
∴AD∥CE.
∵DE∥AC,
∴四边形ACED是平行四边形.
∴DE=AC.
∴BD=DE.
四、巩固练习
6.如图,矩形ABCD中,AC,BD相交于O,AE平分∠BAD交BC于点E,若∠CAE=15°,求∠BOE的度数.
四、巩固练习
解: ∵在矩形ABCD中
∴∠BAD=∠ABC=90°, OA=OB
∵AE平分∠BAD,
∴∠DAE=∠BAE=45°
∴∠AEB=90°- 45°= 45°
∴AB=BE.
∵∠CAE=15°,
∴∠BAO=45°+15°=60°.
∴△BOA是等边三角形.
∴OB=AB, ∠ABO=60°
∴ OB=BE.,∠OBE=30°
∴∠BOE=1/2(180°-30°)=75°.
五、课堂小结
矩形的性质
轴对称 中心对称图形,轴对称图形
边 对边平行且相等
角 四个角都是直角
对角线 相等 且互相平分
直角三角形斜边上中线的性质 :
直角三角形斜边上的中线等于斜边的一半
六、布置作业
课本P13 习题1.4 第1,2,3,4题
谢谢聆听
北师大版九年级上册
第一章
特殊平行四边形
1.2 矩形的性质与判定(一)
一、情景导入
思考:这种平行四边形特殊在哪里?
图片中有你熟悉的图形吗?
定义:有一个角是直角的平行四边形叫做矩形
几何语言:
∵四边形ABCD是平行四边形
∠A=90°( 或∠B=90° )
∴四边形ABCD是矩形
学习概念
★矩形是特殊的平行四边形
A
D
C
B
(1)矩形具有平行四边形的所有性质,你能列举一些这样的性质吗?
(2)你认为矩形还具有哪些特殊的性质?
平行四边形 矩形特殊性质
轴对称 中心对称图形
边 对边平行且相等
角 对角相等
对角线 互相平分
二、探索性质
二、探究矩形的性质
(1)矩形是轴对称图形吗?如果是,请指出它的对称轴.
(2)矩形有什么特殊性质?
结论:
(1)矩形是轴对称图形,有两条对称轴.
(2)矩形的四个角都是直角.
(3)矩形的对角线相等
已知:如图,四边形ABCD是矩形,∠ABC=90°,
对角线AC与BD相交于点O.
求证:(1) ∠ABC=∠BCD=∠CDA=∠DAB =90°;
(2)AC=BD;
求证:矩形的四个角都是直角,对角线相等
A
D
C
B
O
证明:(1)∵四边形ABCD是平行四边形,
∴ ∠ABC=∠CDA, ∠BCD=∠DAB
AD // BC
∴ ∠ABC+∠BCD =180°
又∵ ∠ABC =90°
∴ ∠ABC=∠BCD=∠CDA=∠DAB =90°
(2) ∵四边形ABCD是平行四边形
∴ AD =BC,∠ABC=∠BCD , AB =CD
∴ △ABC ≌△DCB(SAS)
∴AC=BD
A
D
C
B
O
矩形的性质定理:
(1)矩形的四个角都是直角
符号语言:
∵四边形ABCD是矩形
∴ ∠ABC=∠BCD=∠CDA=∠DAB =90°
(2)矩形的对角线相等
符号语言:
∵四边形ABCD是矩形
∴AC=BD
A
D
C
B
O
平行四边形 矩形的特殊性质
轴对称 中心对称图形 轴对称图形
边 对边平行且相等 /
角 对角相等 四个角都是直角
对角线 互相平分 相等
归纳总结
矩形是特殊的平行四边形,除具有平行四边形的所有性质外,还有平行四边形所没有的特殊性质.
如图,矩形ABCD的对角线AC与BD交于点O,思考:
(1)BO是Rt△ABC中斜边AC上什么特殊线段
(2)BO与AC有什么大小关系
D
B
C
A
O
探究直角三角形的性质
猜想:BO 是Rt△ABC中斜边AC上的中线,
且BO等于AC的一半
如图,矩形ABCD的对角线AC与BD交于点O,
求证:(1)BO是Rt△ABC斜边AC上的中线;
(2) BO= AC
D
B
C
A
O
证明:(1) ∵四边形ABCD是矩形
∴O是AC的中点
∴ BO是Rt△ABC斜边AC上的中线
(2) ∵四边形ABCD是矩形
∴AC=BD,OB= BD
∴ OB= AC
总结归纳:
直角三角形斜边上中线的性质
直角三角形斜边上的中线等于斜边的一半
符号语言:
∵ Rt△ABC,O是AC的中点
∴ BO= AC
A
B
C
O
例1:如图,在矩形ABCD中,两条对角线相交于点O,
∠AOD=120°,AB=2.5 ,求矩形对角线的长.
A
B
C
D
O
二、典例精析
证明:∵四边形ABCD是矩形
∴ ∠BAD=90°, AC=BD
OA= AC,OD= BD,
∴ OA= OD
∵∠AOD=120°
∴ ∠OAD= ∠ODA=30 °
在Rt△ABD中,
BD=2AB=2×2.5=5
如图,在矩形ABCD中,两条对角线AC,BD相交于点O,∠ACD=30°,AD=2.
(1)判断△AOD的形状;
(2)求对角线AC的长.
变式练习
解:(1)∵四边形ABCD为矩形,
∴∠ADC=90°,OA=OD=OC=OB.
∵∠ACD=30°,
∴∠DAC=90°- 30°=60°.
而∵ OA=OD
∴△AOD为等边三角形.
(2)∵△AOD为等边三角形,∴AO=AD=2.
∴AC=2AO=4.
四、巩固练习
1.如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=2,则矩形的边长BC的长是( )
A.2 B.4 C.2 D.4
C
2. 如图,在 ABCD中,对角线AC,BD相交于点O,OA=OB,若AD=4,∠AOD=60°,则AB的长( )
A. 4 B. 2 C. 8 D. 8
A
四、巩固练习
四、巩固练习
3. 如图,矩形ABCD的对角线AC,BD交于点O,∠AOD=60°,AB=2 ,AE⊥BD于点E,则OE的长为________.
1
4.如图,在矩形ABCD中,O是对角线AC的中点,OM∥AB交AD于点M,若OM=3,BC=10,则OB的长为( )
A. 5 B. 4 C. D.
D
2
___
四、巩固练习
5.已知:如图,在矩形ABCD中,对角线AC,BD相交于点O,过点D作DE∥AC交BC延长线于点E.
求证:BD=DE.
证明:在矩形ABCD中,
∴AC=BD,AD∥BC
∴AD∥CE.
∵DE∥AC,
∴四边形ACED是平行四边形.
∴DE=AC.
∴BD=DE.
四、巩固练习
6.如图,矩形ABCD中,AC,BD相交于O,AE平分∠BAD交BC于点E,若∠CAE=15°,求∠BOE的度数.
四、巩固练习
解: ∵在矩形ABCD中
∴∠BAD=∠ABC=90°, OA=OB
∵AE平分∠BAD,
∴∠DAE=∠BAE=45°
∴∠AEB=90°- 45°= 45°
∴AB=BE.
∵∠CAE=15°,
∴∠BAO=45°+15°=60°.
∴△BOA是等边三角形.
∴OB=AB, ∠ABO=60°
∴ OB=BE.,∠OBE=30°
∴∠BOE=1/2(180°-30°)=75°.
五、课堂小结
矩形的性质
轴对称 中心对称图形,轴对称图形
边 对边平行且相等
角 四个角都是直角
对角线 相等 且互相平分
直角三角形斜边上中线的性质 :
直角三角形斜边上的中线等于斜边的一半
六、布置作业
课本P13 习题1.4 第1,2,3,4题
谢谢聆听
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
