21.3二次函数与一元二次方程(3) 教学课件(共33张PPT)
文档属性
| 名称 | 21.3二次函数与一元二次方程(3) 教学课件(共33张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-06 00:00:00 | ||
图片预览




文档简介
(共33张PPT)
沪科版 九年级上册
21.3二次函数与一元二次方程(3)
教学目标
探索二次函数与一元二次不等式的关系的过程,体会不等式与函数之间的联系.利用图象法求一元二次不等式的解集,体会不等式与函数之间的关系,学生综合解题能力,渗透数形结合思想.
教学重点:利用图象法求一元二次不等式的解集.
教学难点:进一步培养学生综合解题能力,渗透
数形结合思想.
b2-4ac的符号:
确定抛物线与x轴交点个数
x
y
O
与x轴有2个交点
与x轴有1个交点
与x轴没有交点
b2-4ac>0
b2-4ac=0
b2-4ac<0
复习旧知
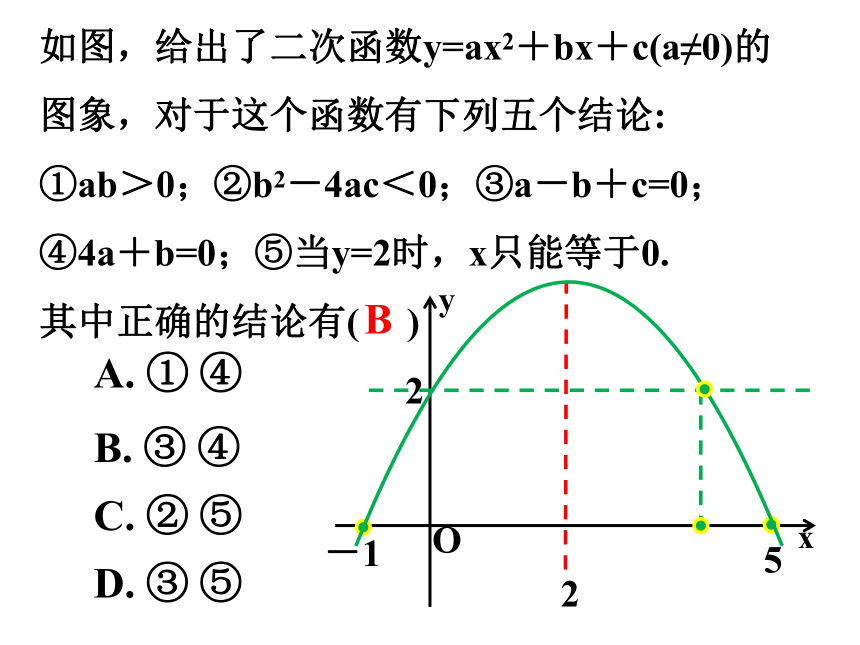
如图,给出了二次函数y=ax2+bx+c(a≠0)的图象,对于这个函数有下列五个结论:
①ab>0;②b2-4ac<0;③a-b+c=0;
④4a+b=0;⑤当y=2时,x只能等于0.
其中正确的结论有( )
A. ① ④
C. ② ⑤
B. ③ ④
D. ③ ⑤
B
O
x
y
-1
5
2
2
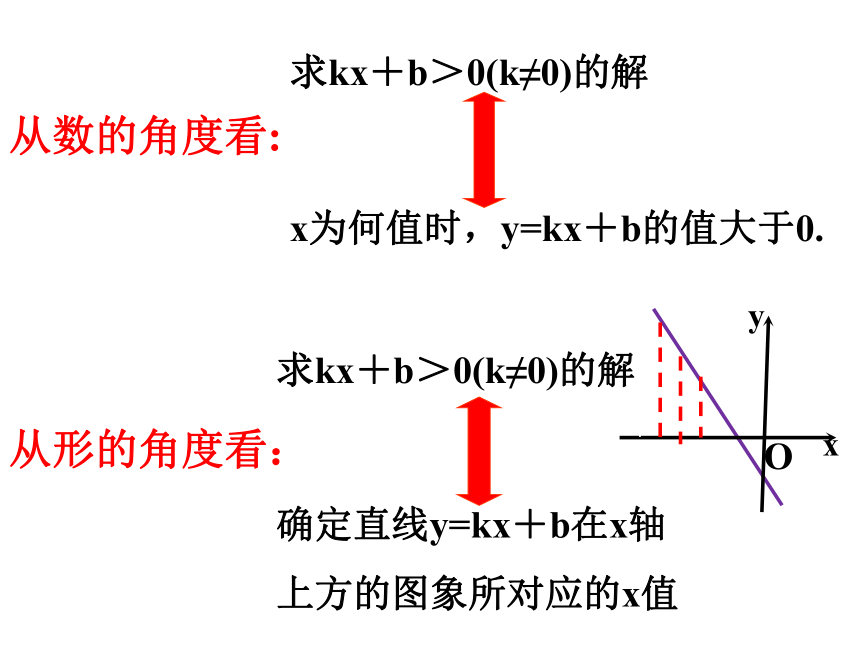
求kx+b>0(k≠0)的解
x为何值时,y=kx+b的值大于0.
确定直线y=kx+b在x轴
上方的图象所对应的x值
从形的角度看:
从数的角度看:
求kx+b>0(k≠0)的解
x
y
O
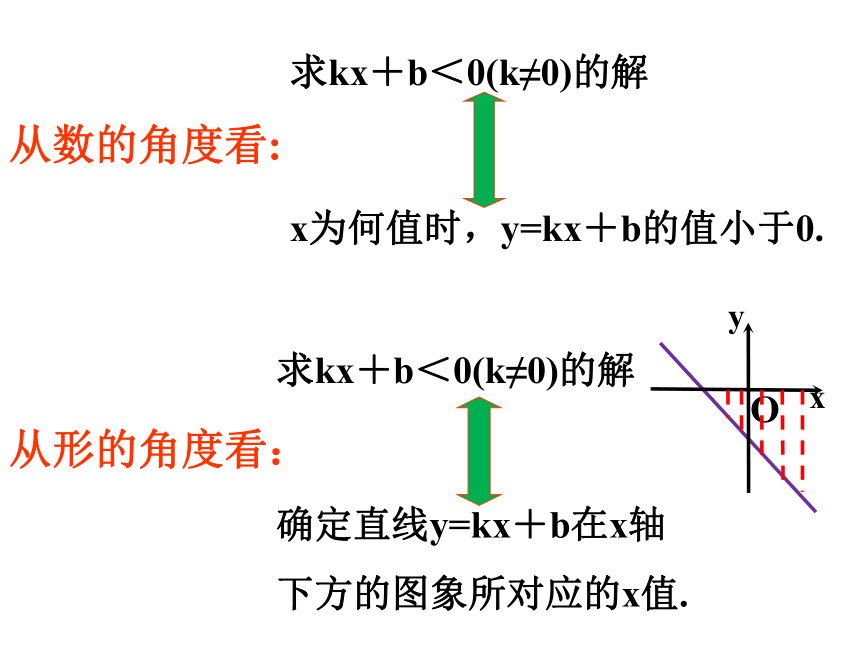
求kx+b<0(k≠0)的解
x为何值时,y=kx+b的值小于0.
确定直线y=kx+b在x轴
下方的图象所对应的x值.
从形的角度看:
从数的角度看:
求kx+b<0(k≠0)的解
x
y
O
二次函数与一元二次不等式有怎样的关系?
阅读教材P33阅读与思考部分,
探索一元二次不等式
x2+3x+2>0,x2+3x+2<0的解集
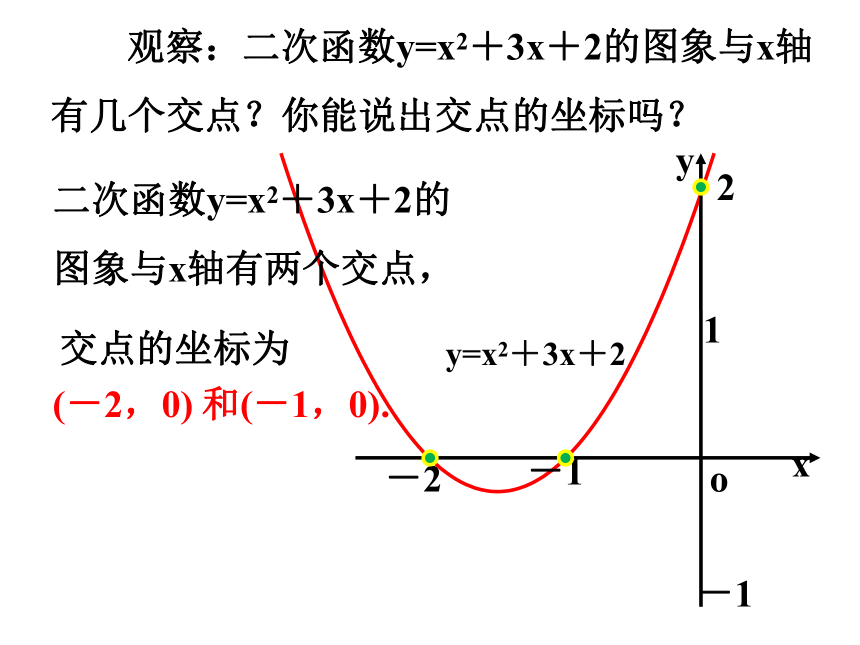
观察:二次函数y=x2+3x+2的图象与x轴有几个交点?你能说出交点的坐标吗?
x
y
o
-1
1
2
-2
-1
y=x2+3x+2
二次函数y=x2+3x+2的图象与x轴有两个交点,
交点的坐标为
(-2,0)
和(-1,0).
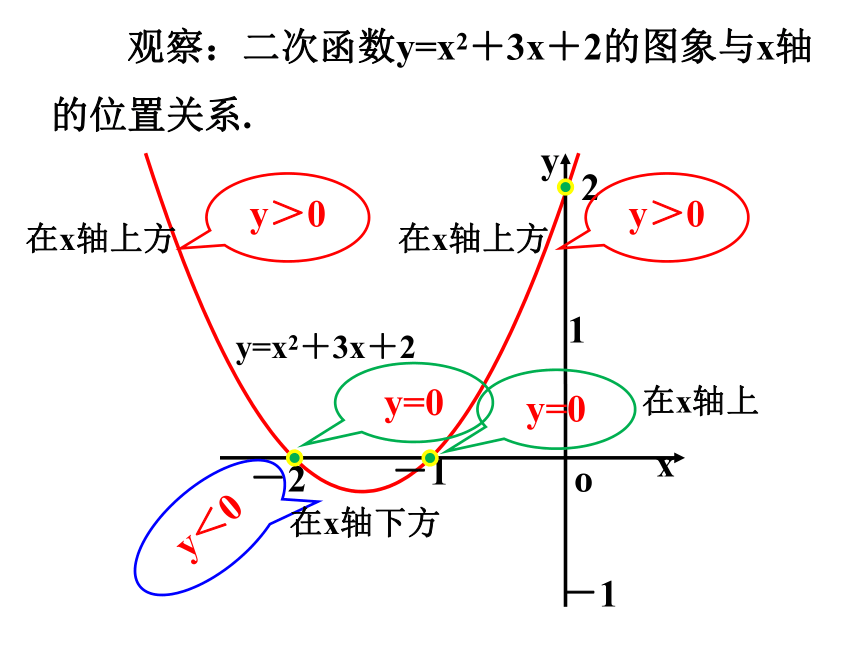
观察:二次函数y=x2+3x+2的图象与x轴的位置关系.
x
y
o
-1
1
2
-2
-1
y=x2+3x+2
y>0
y>0
y=0
y=0
y<0
在x轴上
在x轴上方
在x轴上方
在x轴下方
x
y
o
-1
1
2
-2
-1
y=x2+3x+2
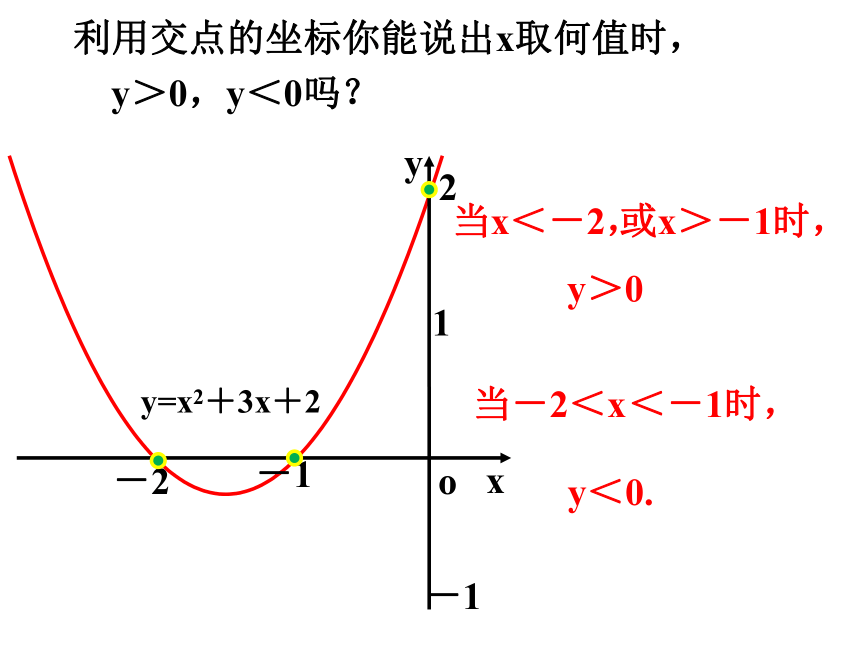
利用交点的坐标你能说出x取何值时,
y>0,y<0吗?
当x<-2,
或x>-1时,
<-1时,
当-2<x
y>0
y<0.
x
y
o
-1
2
-2
-1
y=x2+3x+2
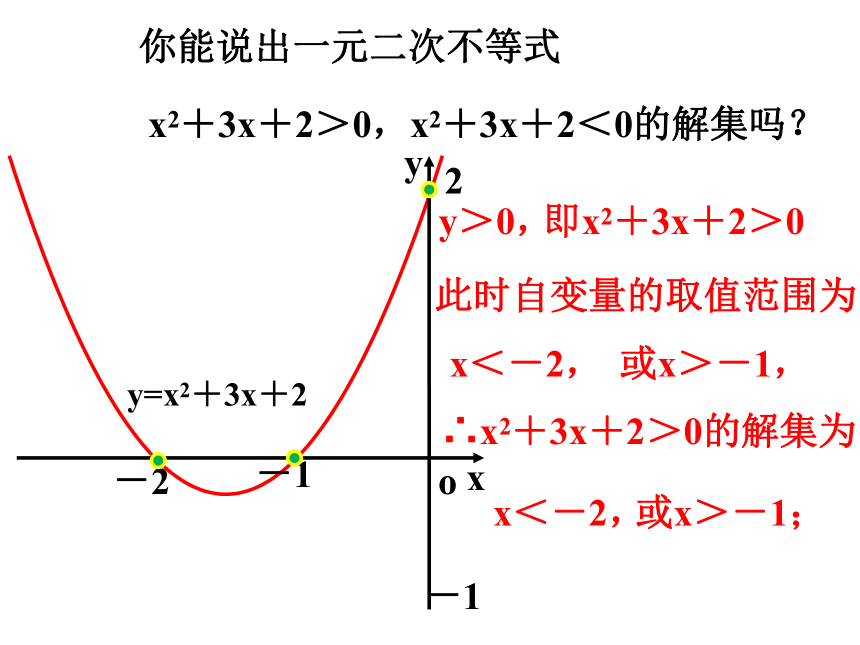
你能说出一元二次不等式
x2+3x+2>0,x2+3x+2<0的解集吗?
∴x2+3x+2>0的解集为
x<-2,
或x>-1;
y>0,
即x2+3x+2>0
x<-2,
或x>-1,
此时自变量的取值范围为
x
y
o
-1
2
-2
-1
y=x2+3x+2
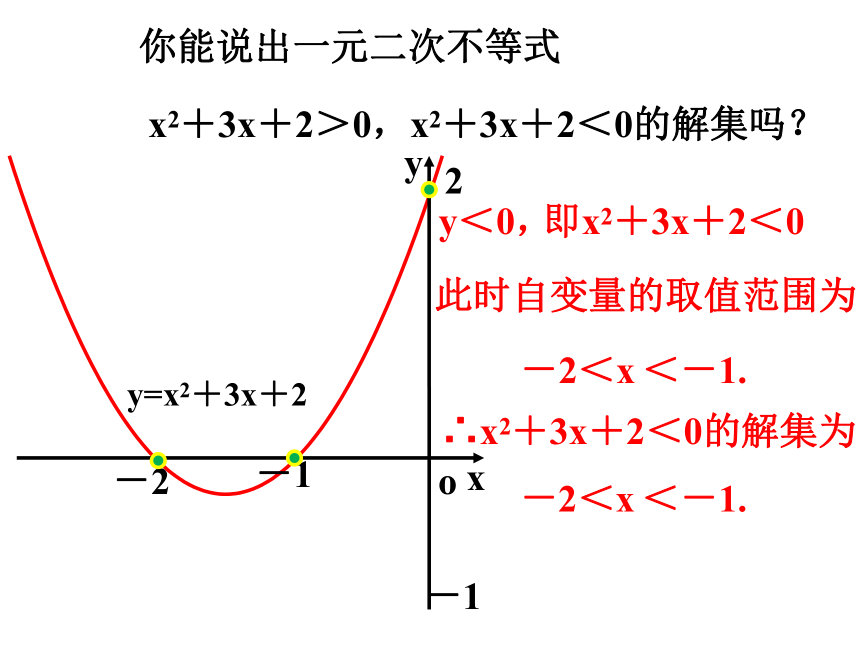
你能说出一元二次不等式
x2+3x+2>0,x2+3x+2<0的解集吗?
∴x2+3x+2<0的解集为
y<0,
即x2+3x+2<0
此时自变量的取值范围为
<-1.
-2<x
<-1.
-2<x
x
y
o
-1
1
2
-2
-1
y=x2+3x+2
你能说出一元二次不等式
x2+3x+2>0,x2+3x+2<0的解集吗?
x2+3x+2>0的解集为
x<-2,
或x>-1;
x2+3x+2< 0的解集为
<-1.
-2<x
1.先求出一元二次方程x2+2x-1=0 的根,再
结合二次函数y=x2+2x-1的图象,求出当
y=x2+2x-1>0,y=x2+2x-1<0时,x的
取值范围.
x2+2x-1=0
x2+2x=1
x2+2x+1=1+1
(x+1)2=2
x+1=
±
2
x1= -1,
2
x2=- -1 .
2
解:
练习巩固
*
x
y
o
-1
1
-3
-1
-2
-2
y=x2+2x-1
x1= -1
2
x2=- -1
2
当 y=x2+2x-1>0时,
x的取值 范围为:
x<
- -1 ,
2
或x> .
-1
2
1.先求出一元二次方程x2+2x-1=0 的根,再结
合二次函数y=x2+2x-1的图象,求出当y=x2+
2x-1>0,y=x2+2x-1<0时,x的取值范围.
*
x
y
o
-1
1
-3
-1
-2
-2
y=x2+2x-1
1.先求出一元二次方程x2+2x-1=0 的根,再结
合二次函数y=x2+2x-1的图象,求出当y=x2+
2x-1>0,y=x2+2x-1<0时,x的取值范围.
x1= -1
2
x2=- -1
2
当 y=x2+2x-1<0时,
x的取值 范围为:
< x<
- -1
2
-1
2
*
x
y
o
-1
1
-1
-5
2.结合二次函数y=-2x2+3x-5的图象,求:
(1)-2x2+3x-5>0的解集;
(2)-2x2+3x-5<0的解集.
(1)无解
(2)全体实数.
y=-2x2+3x-5
求ax2+bx+c>0的解
x为何值时, y=ax2+bx+c的值大于0.
确定抛物线y= ax2+bx+c在
x轴上方的图象所对应的x值
从形的角度看:
从数的角度看:
求ax2+bx+c>0的解
x
y
O
求ax2+bx+c<0的解
x为何值时, y=ax2+bx+c的值小于0.
确定抛物线y= ax2+bx+c在
x轴下方的图象所对应的x值
从形的角度看:
从数的角度看:
求ax2+bx+c<0的解
x
y
O
1.已知二次函数y=x2-2x-3的图象如图,当
y<0时,的取值范围是( ).
A.x<-1
B.x>3
C. -1<x<3
D.x<-1或x>3
练习巩固
x
y
O
-1
3
y=x2-2x-3
C
2.已知函数y=ax2+bx+c的图象如图所示,
则方程ax2+bx+c =0的根是 ;
不等式ax2+bx+c>0的解集是 ;
不等式ax2+bx+c<0 的解集是 .
x1=-1,
x2=5
-1<x<5
x<-1或x>5
x
y
O
2
5
3.二次函数y=ax2+bx+c的图象与x轴相交于
(-2,0)和(4,0)两点当函数值y<0时,x的取
范围是( ).
A.x<-2
B. - 2C.x>4
D.x<-2或x>4
x
y
O
-2
4
D
4.如图是二次函数y=ax2+bx+c图象的一部
分,当y>0时,x的取值范围是( ).
A.x<-1或x>2
B.x<-1或x>5
C.-1<x<5
D. -1<x<2
x
y
O
2
-1
B
5.二次函数y=ax2+bx+c的图象如图所示,则
关于上的不等式ax2+bx+c<0的解集是( ).
A.x<-1
B.x<2
C.-1<x<2
D. x<-1或x>2
x
y
O
2
-1
C
6.如图是二次函数y=ax2+bx+c的部分图象.由图
象可知,不等式y=ax2+bx+c>0的解集是( ).
A.x>3
B.x<-1
C.-1<x<3
D. x<-1或x>3
x
y
O
1
3
C
6.二次函数y=x2-2x-1的图象如图 所示,当
y<2时,x的取值范围是( ).
A. -1≤x≤3
B. x≥-2
C. -2≤x≤2
D. x≤-1或x≥3
x
y
O
3
-1
2
-1
-2
1
A
7.如图,已知二次函数y1= x2- x的图象与正
比例函数y2= x的图象交于点A(3,2),与x
轴交于点B(2,0)、如果0值范围是( ).
A.0B. 0C.2D.x<0或x>3
2
3
4
3
2
3
C
x
y
O
3
-1
2
B
A
1
8.已知二次函数y=x2+2x+m的图象与x轴只有
一个交点,则关于x的不等式x2+2x+m>0的
解集是 .
x≠-1
9.如图,函数y1=ax 与y2=bx+c的图象相交于A
(-2,4),B(1,1)两点,则关于的一元二次方
程ax2-bx-c=0的根是 ,
当y1>y2时,x的取值范围是 ;
当y1x
y
O
-2
B
A
2
x1=-2,
x2=1
x1<-2,
或x2>1
-2<x<1
今天作业
课本P35页第8、9题
二次函数与一元二次不等式的关系:
一元二次不等式ax2+bx+c>0的解集就是二次函数y=ax2+bx+c 的图象位于x轴上方的点对应的自变量的取值范围,一元二次不等式ax2+bx+c<0的解集就是二次函数y=ax2+bx+c 的图象位于x轴下方的点对应的自变量的取值范围.因此可用图象法求一元二次不等式的解集.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 九年级上册
21.3二次函数与一元二次方程(3)
教学目标
探索二次函数与一元二次不等式的关系的过程,体会不等式与函数之间的联系.利用图象法求一元二次不等式的解集,体会不等式与函数之间的关系,学生综合解题能力,渗透数形结合思想.
教学重点:利用图象法求一元二次不等式的解集.
教学难点:进一步培养学生综合解题能力,渗透
数形结合思想.
b2-4ac的符号:
确定抛物线与x轴交点个数
x
y
O
与x轴有2个交点
与x轴有1个交点
与x轴没有交点
b2-4ac>0
b2-4ac=0
b2-4ac<0
复习旧知
如图,给出了二次函数y=ax2+bx+c(a≠0)的图象,对于这个函数有下列五个结论:
①ab>0;②b2-4ac<0;③a-b+c=0;
④4a+b=0;⑤当y=2时,x只能等于0.
其中正确的结论有( )
A. ① ④
C. ② ⑤
B. ③ ④
D. ③ ⑤
B
O
x
y
-1
5
2
2
求kx+b>0(k≠0)的解
x为何值时,y=kx+b的值大于0.
确定直线y=kx+b在x轴
上方的图象所对应的x值
从形的角度看:
从数的角度看:
求kx+b>0(k≠0)的解
x
y
O
求kx+b<0(k≠0)的解
x为何值时,y=kx+b的值小于0.
确定直线y=kx+b在x轴
下方的图象所对应的x值.
从形的角度看:
从数的角度看:
求kx+b<0(k≠0)的解
x
y
O
二次函数与一元二次不等式有怎样的关系?
阅读教材P33阅读与思考部分,
探索一元二次不等式
x2+3x+2>0,x2+3x+2<0的解集
观察:二次函数y=x2+3x+2的图象与x轴有几个交点?你能说出交点的坐标吗?
x
y
o
-1
1
2
-2
-1
y=x2+3x+2
二次函数y=x2+3x+2的图象与x轴有两个交点,
交点的坐标为
(-2,0)
和(-1,0).
观察:二次函数y=x2+3x+2的图象与x轴的位置关系.
x
y
o
-1
1
2
-2
-1
y=x2+3x+2
y>0
y>0
y=0
y=0
y<0
在x轴上
在x轴上方
在x轴上方
在x轴下方
x
y
o
-1
1
2
-2
-1
y=x2+3x+2
利用交点的坐标你能说出x取何值时,
y>0,y<0吗?
当x<-2,
或x>-1时,
<-1时,
当-2<x
y>0
y<0.
x
y
o
-1
2
-2
-1
y=x2+3x+2
你能说出一元二次不等式
x2+3x+2>0,x2+3x+2<0的解集吗?
∴x2+3x+2>0的解集为
x<-2,
或x>-1;
y>0,
即x2+3x+2>0
x<-2,
或x>-1,
此时自变量的取值范围为
x
y
o
-1
2
-2
-1
y=x2+3x+2
你能说出一元二次不等式
x2+3x+2>0,x2+3x+2<0的解集吗?
∴x2+3x+2<0的解集为
y<0,
即x2+3x+2<0
此时自变量的取值范围为
<-1.
-2<x
<-1.
-2<x
x
y
o
-1
1
2
-2
-1
y=x2+3x+2
你能说出一元二次不等式
x2+3x+2>0,x2+3x+2<0的解集吗?
x2+3x+2>0的解集为
x<-2,
或x>-1;
x2+3x+2< 0的解集为
<-1.
-2<x
1.先求出一元二次方程x2+2x-1=0 的根,再
结合二次函数y=x2+2x-1的图象,求出当
y=x2+2x-1>0,y=x2+2x-1<0时,x的
取值范围.
x2+2x-1=0
x2+2x=1
x2+2x+1=1+1
(x+1)2=2
x+1=
±
2
x1= -1,
2
x2=- -1 .
2
解:
练习巩固
*
x
y
o
-1
1
-3
-1
-2
-2
y=x2+2x-1
x1= -1
2
x2=- -1
2
当 y=x2+2x-1>0时,
x的取值 范围为:
x<
- -1 ,
2
或x> .
-1
2
1.先求出一元二次方程x2+2x-1=0 的根,再结
合二次函数y=x2+2x-1的图象,求出当y=x2+
2x-1>0,y=x2+2x-1<0时,x的取值范围.
*
x
y
o
-1
1
-3
-1
-2
-2
y=x2+2x-1
1.先求出一元二次方程x2+2x-1=0 的根,再结
合二次函数y=x2+2x-1的图象,求出当y=x2+
2x-1>0,y=x2+2x-1<0时,x的取值范围.
x1= -1
2
x2=- -1
2
当 y=x2+2x-1<0时,
x的取值 范围为:
< x<
- -1
2
-1
2
*
x
y
o
-1
1
-1
-5
2.结合二次函数y=-2x2+3x-5的图象,求:
(1)-2x2+3x-5>0的解集;
(2)-2x2+3x-5<0的解集.
(1)无解
(2)全体实数.
y=-2x2+3x-5
求ax2+bx+c>0的解
x为何值时, y=ax2+bx+c的值大于0.
确定抛物线y= ax2+bx+c在
x轴上方的图象所对应的x值
从形的角度看:
从数的角度看:
求ax2+bx+c>0的解
x
y
O
求ax2+bx+c<0的解
x为何值时, y=ax2+bx+c的值小于0.
确定抛物线y= ax2+bx+c在
x轴下方的图象所对应的x值
从形的角度看:
从数的角度看:
求ax2+bx+c<0的解
x
y
O
1.已知二次函数y=x2-2x-3的图象如图,当
y<0时,的取值范围是( ).
A.x<-1
B.x>3
C. -1<x<3
D.x<-1或x>3
练习巩固
x
y
O
-1
3
y=x2-2x-3
C
2.已知函数y=ax2+bx+c的图象如图所示,
则方程ax2+bx+c =0的根是 ;
不等式ax2+bx+c>0的解集是 ;
不等式ax2+bx+c<0 的解集是 .
x1=-1,
x2=5
-1<x<5
x<-1或x>5
x
y
O
2
5
3.二次函数y=ax2+bx+c的图象与x轴相交于
(-2,0)和(4,0)两点当函数值y<0时,x的取
范围是( ).
A.x<-2
B. - 2
D.x<-2或x>4
x
y
O
-2
4
D
4.如图是二次函数y=ax2+bx+c图象的一部
分,当y>0时,x的取值范围是( ).
A.x<-1或x>2
B.x<-1或x>5
C.-1<x<5
D. -1<x<2
x
y
O
2
-1
B
5.二次函数y=ax2+bx+c的图象如图所示,则
关于上的不等式ax2+bx+c<0的解集是( ).
A.x<-1
B.x<2
C.-1<x<2
D. x<-1或x>2
x
y
O
2
-1
C
6.如图是二次函数y=ax2+bx+c的部分图象.由图
象可知,不等式y=ax2+bx+c>0的解集是( ).
A.x>3
B.x<-1
C.-1<x<3
D. x<-1或x>3
x
y
O
1
3
C
6.二次函数y=x2-2x-1的图象如图 所示,当
y<2时,x的取值范围是( ).
A. -1≤x≤3
B. x≥-2
C. -2≤x≤2
D. x≤-1或x≥3
x
y
O
3
-1
2
-1
-2
1
A
7.如图,已知二次函数y1= x2- x的图象与正
比例函数y2= x的图象交于点A(3,2),与x
轴交于点B(2,0)、如果0
A.0
2
3
4
3
2
3
C
x
y
O
3
-1
2
B
A
1
8.已知二次函数y=x2+2x+m的图象与x轴只有
一个交点,则关于x的不等式x2+2x+m>0的
解集是 .
x≠-1
9.如图,函数y1=ax 与y2=bx+c的图象相交于A
(-2,4),B(1,1)两点,则关于的一元二次方
程ax2-bx-c=0的根是 ,
当y1>y2时,x的取值范围是 ;
当y1
y
O
-2
B
A
2
x1=-2,
x2=1
x1<-2,
或x2>1
-2<x<1
今天作业
课本P35页第8、9题
二次函数与一元二次不等式的关系:
一元二次不等式ax2+bx+c>0的解集就是二次函数y=ax2+bx+c 的图象位于x轴上方的点对应的自变量的取值范围,一元二次不等式ax2+bx+c<0的解集就是二次函数y=ax2+bx+c 的图象位于x轴下方的点对应的自变量的取值范围.因此可用图象法求一元二次不等式的解集.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
