一元二次方程的解法(2)因式分解法
图片预览

文档简介
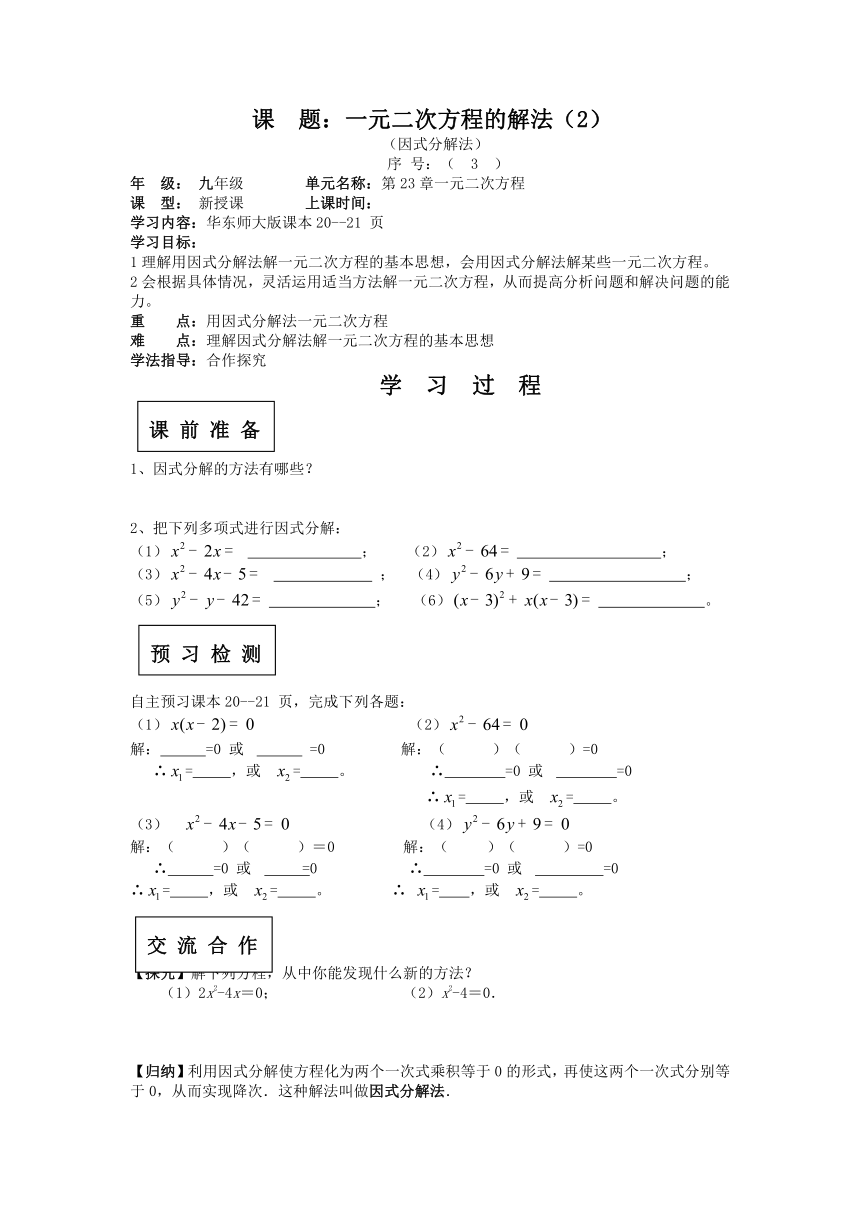
课 题:一元二次方程的解法(2)
(因式分解法)
序 号:( 3 )
年 级: 九年级 单元名称:第23章一元二次方程
课 型: 新授课 上课时间:
学习内容:华东师大版课本20--21 页
学习目标:
1理解用因式分解法解一元二次方程的基本思想,会用因式分解法解某些一元二次方程。
2会根据具体情况,灵活运用适当方法解一元二次方程,从而提高分析问题和解决问题的能力。
重 点:用因式分解法一元二次方程
难 点:理解因式分解法解一元二次方程的基本思想
学法指导:合作探究
学 习 过 程
因式分解的方法有哪些?
2、把下列多项式进行因式分解:
(1) ; (2) ;
(3) ; (4) ;
(5) ; (6) 。
自主预习课本20--21 页,完成下列各题:
(1) (2)
解: =0 或 =0 解:( )( )=0
∴= ,或= 。 ∴ =0 或 =0
∴= ,或= 。
(3) (4)
解:( )( )=0 解:( )( )=0
∴ =0 或 =0 ∴ =0 或 =0
∴= ,或= 。 ∴ = ,或= 。
【探究】解下列方程,从中你能发现什么新的方法?
(1)2x2-4x=0; (2)x2-4=0.
【归纳】利用因式分解使方程化为两个一次式乘积等于0的形式,再使这两个一次式分别等于0,从而实现降次.这种解法叫做因式分解法.
【例1】用因式分解法解方程:
(2)x2-3x-10=0 ⑶9x2+6x-3=0 ⑷4x2-4x+1=0
【说明】能用因式分解法解的一元二次方程的特征是:方程的一边是0,另一边可以分解因式。
跟踪练习1: (1) (2) (3)x2-11x+28=0
【说明】用因式分解法解一元二次方程时,要根据情况灵活选用学过的因式分解的几种方法,不能出现失根的情况。如解方程时,方程两边同除以x, 得x=4,这样就失掉了x=0这一个根。
【例2】用因式分解法解方程:
⑴x(x-2)+x-2=0 ⑵3x(x+2)=5(x+2) (3)
【说明】此题重在培养学生整体思想方法的运用。
跟踪练习2:
(1) (2)x(2x-5)=4x-10 (3)
【例3】用因式分解法解方程:
(1)(x+3)(x-1)=5 (2)5x2-2x-=x2-2x+
【分析】这几个方程可以展开整理成一元二次方程的一般形式,然后根据这两个方程的特点,直接应用因式分解法较简便。
跟踪练习3: (1) ⑵x2+5x+7=3x+11
【小结】因式分解法解一元二次方程的步骤:
将一元二次方程化成一般形式,即方程右边为0。
将方程左边进行因式分解,由一元二次方程转化成两个一元一次方程。
对两个一元一次方程分别求解。
【强调】将原方程变形为一边是0,这一步很重要,因为只有当一边是0,即两个因式的积是0,两个因式才分别是0,从而得到两个一元一次方程。
【例4】选择合适的方法解方程:
(2)
跟踪练习4:选择合适的方法解方程。
(1)x2-6x+9=(5-2x)2 (2)(3x+1)2-5=0 (3)
1.用因式分解法解方程:
(1) (2)
解:由原方程得: 解:=0
=0 或 =0 ∴ =0 或 =0
∴= ,= ∴= ,=
2.用因式分解法解下列方程:
(1) (2)
(4)
(6)
(8)
3.用适当的方法解下列方程:
(1)9x2+6x+1=0 (2)3x2-6x=-3 (3)(x-2)2-4=0
4.用两种方法解下列方程:
(1)25y2-16=0 (2)(x-4)2=(5-2x) 2
(因式分解法)
序 号:( 3 )
年 级: 九年级 单元名称:第23章一元二次方程
课 型: 新授课 上课时间:
学习内容:华东师大版课本20--21 页
学习目标:
1理解用因式分解法解一元二次方程的基本思想,会用因式分解法解某些一元二次方程。
2会根据具体情况,灵活运用适当方法解一元二次方程,从而提高分析问题和解决问题的能力。
重 点:用因式分解法一元二次方程
难 点:理解因式分解法解一元二次方程的基本思想
学法指导:合作探究
学 习 过 程
因式分解的方法有哪些?
2、把下列多项式进行因式分解:
(1) ; (2) ;
(3) ; (4) ;
(5) ; (6) 。
自主预习课本20--21 页,完成下列各题:
(1) (2)
解: =0 或 =0 解:( )( )=0
∴= ,或= 。 ∴ =0 或 =0
∴= ,或= 。
(3) (4)
解:( )( )=0 解:( )( )=0
∴ =0 或 =0 ∴ =0 或 =0
∴= ,或= 。 ∴ = ,或= 。
【探究】解下列方程,从中你能发现什么新的方法?
(1)2x2-4x=0; (2)x2-4=0.
【归纳】利用因式分解使方程化为两个一次式乘积等于0的形式,再使这两个一次式分别等于0,从而实现降次.这种解法叫做因式分解法.
【例1】用因式分解法解方程:
(2)x2-3x-10=0 ⑶9x2+6x-3=0 ⑷4x2-4x+1=0
【说明】能用因式分解法解的一元二次方程的特征是:方程的一边是0,另一边可以分解因式。
跟踪练习1: (1) (2) (3)x2-11x+28=0
【说明】用因式分解法解一元二次方程时,要根据情况灵活选用学过的因式分解的几种方法,不能出现失根的情况。如解方程时,方程两边同除以x, 得x=4,这样就失掉了x=0这一个根。
【例2】用因式分解法解方程:
⑴x(x-2)+x-2=0 ⑵3x(x+2)=5(x+2) (3)
【说明】此题重在培养学生整体思想方法的运用。
跟踪练习2:
(1) (2)x(2x-5)=4x-10 (3)
【例3】用因式分解法解方程:
(1)(x+3)(x-1)=5 (2)5x2-2x-=x2-2x+
【分析】这几个方程可以展开整理成一元二次方程的一般形式,然后根据这两个方程的特点,直接应用因式分解法较简便。
跟踪练习3: (1) ⑵x2+5x+7=3x+11
【小结】因式分解法解一元二次方程的步骤:
将一元二次方程化成一般形式,即方程右边为0。
将方程左边进行因式分解,由一元二次方程转化成两个一元一次方程。
对两个一元一次方程分别求解。
【强调】将原方程变形为一边是0,这一步很重要,因为只有当一边是0,即两个因式的积是0,两个因式才分别是0,从而得到两个一元一次方程。
【例4】选择合适的方法解方程:
(2)
跟踪练习4:选择合适的方法解方程。
(1)x2-6x+9=(5-2x)2 (2)(3x+1)2-5=0 (3)
1.用因式分解法解方程:
(1) (2)
解:由原方程得: 解:=0
=0 或 =0 ∴ =0 或 =0
∴= ,= ∴= ,=
2.用因式分解法解下列方程:
(1) (2)
(4)
(6)
(8)
3.用适当的方法解下列方程:
(1)9x2+6x+1=0 (2)3x2-6x=-3 (3)(x-2)2-4=0
4.用两种方法解下列方程:
(1)25y2-16=0 (2)(x-4)2=(5-2x) 2
