测量1
图片预览

文档简介
课 题:《测量》
序 号: ( 1 )
年 级: 九年级 单元名称:第25章解直角三角形
课 型: 新授课 上课时间:
学习内容:华东师大版86--87页
学习目标:
利用前面学习的相似三角形的有关知识,探索测量距离的几种方法,初步接触直角三角形的边角关系。
重 点:探索测量距离的几种方法。
难 点:选择适当的方法测量物体的高度或长度
学法指导:自主预习,合作探究
学 习 过 程
三角形相似的判断方法有哪些?
相似三角形有什么性质?
有个三边长分别是3米,4米,5米的三角形花坛,请你按1:100的比例将它画在下面。
自主预习教材86---87页内容,完成下列题目:
小明想知道学校旗杆的高度,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,求旗杆的高度.
2. 请你设计一个切实可行的方案,测量你们学校楼房的高度。
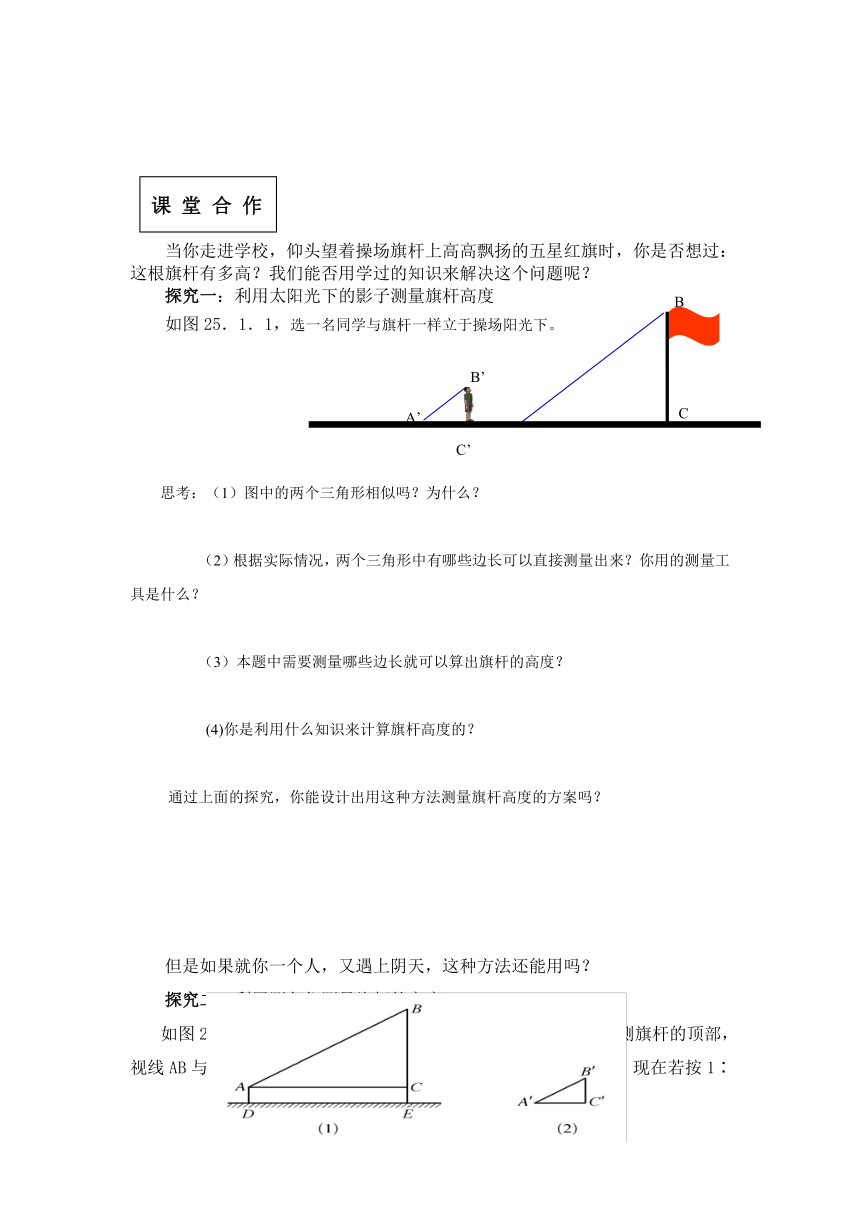
当你走进学校,仰头望着操场旗杆上高高飘扬的五星红旗时,你是否想过:这根旗杆有多高?我们能否用学过的知识来解决这个问题呢?
探究一:利用太阳光下的影子测量旗杆高度
如图25.1.1,选一名同学与旗杆一样立于操场阳光下。
思考:(1)图中的两个三角形相似吗?为什么?
(2)根据实际情况,两个三角形中有哪些边长可以直接测量出来?你用的测量工具是什么?
(3)本题中需要测量哪些边长就可以算出旗杆的高度?
(4)你是利用什么知识来计算旗杆高度的?
通过上面的探究,你能设计出用这种方法测量旗杆高度的方案吗?
但是如果就你一个人,又遇上阴天,这种方法还能用吗?
探究二:利用测角仪测量旗杆的高度
如图25.1.2所示,站在离旗杆BE底部10米处的D点,目测旗杆的顶部,视线AB与水平线的夹角∠BAC为34°,并已知目高AD为1.5米.现在若按1∶500的比例将△ABC画在纸上,并记为△A′B′C′,用刻度直尺量出纸上B′C′的长度,便可以算出旗杆的实际高度.
你知道计算的方法吗?(提示:先测量出教材上图25.1.2中B′C′的长度)
学以致用: 知识链接 教材87页 习题25.1 1 2 3题
拓展提高:
探究三:利用标杆测量旗杆的高度
选一名同学做观测者,在观测者与旗杆之间的地面上直立一根高度适当的标杆,观测者适当调整自己所处的位置,当旗杆的顶部,标杆的顶端与眼睛恰好在一条直线上时,其他同学立即测出观测者的脚到旗杆底部的距离,以及观测者的脚到标杆底部的距离,然后,测得标杆的高,利用相似三角形相关知识计算。
探究四: 利用平面镜反射测量旗杆的高度
选一位同学作为观测者,在观测者与旗杆之间的地面上平放一面镜子,在镜子上做标记
观测者看着镜子来回移动,直至看到旗杆顶端在镜子上的标记重合,测数据,利用相似
三角形的判定及性质可求出旗杆的长。
应用提高:
设计一种方案,测量学校教学楼的高度。请写出测量的过程,并简要说明这样做的理由。
分析:测量大楼的高度的方法很多,现采用一种方法,利用人的身高和标杆,依据相似三角形三边对应成比例和平行线的性质,可测出大楼的高度。
解答:测量过程如下:
1、在地面上立一个标杆,使人眼、杆顶、楼顶在一条直线上。
2、测出CF、CH的距离。
大楼 3、算出KE的长度。
4、用标杆长度减去人的身高,即DE的长度。
标杆 5、由DE∥AB得△KDE∽△KAB。又因为相似三角形三边对应成比例,∴。
6、再将刚才测量的数值代入比例式中,计算出AB的长度。
7、用AB加上人的身高即得出大楼的高度。
探究点拔:1.选择测量的方法应是切实可行的。如本题中人眼、杆顶、楼顶在一条直线上(人是站立的)。
2.大楼的高度=AB+人高。
3.测量的过程要清楚,力求每步都有根有据,达到学以致用。
1.如图1,要测量A、B两点间距离,在O点设桩,取OA中点C, OB中点D,测得CD=31.4m 求AB长。 (AB=62.8m)
(2)
2. 如图2, 为了测量河的宽度,可以先在河对岸找到一个具有明显标志的点A,再在所在的一边找到两点B、C,使△ABC构成Rt△。如果测得BC=50米,∠ABC=73°,试设计一种方法求河的宽度AC。 (在地面上另作 Rt△A’B’C’,使B’C’=5米,∠C’=Rt∠,∠B’=73°, 测得 A’C’=16.35米,得 AC=16.35米 ).
序 号: ( 1 )
年 级: 九年级 单元名称:第25章解直角三角形
课 型: 新授课 上课时间:
学习内容:华东师大版86--87页
学习目标:
利用前面学习的相似三角形的有关知识,探索测量距离的几种方法,初步接触直角三角形的边角关系。
重 点:探索测量距离的几种方法。
难 点:选择适当的方法测量物体的高度或长度
学法指导:自主预习,合作探究
学 习 过 程
三角形相似的判断方法有哪些?
相似三角形有什么性质?
有个三边长分别是3米,4米,5米的三角形花坛,请你按1:100的比例将它画在下面。
自主预习教材86---87页内容,完成下列题目:
小明想知道学校旗杆的高度,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,求旗杆的高度.
2. 请你设计一个切实可行的方案,测量你们学校楼房的高度。
当你走进学校,仰头望着操场旗杆上高高飘扬的五星红旗时,你是否想过:这根旗杆有多高?我们能否用学过的知识来解决这个问题呢?
探究一:利用太阳光下的影子测量旗杆高度
如图25.1.1,选一名同学与旗杆一样立于操场阳光下。
思考:(1)图中的两个三角形相似吗?为什么?
(2)根据实际情况,两个三角形中有哪些边长可以直接测量出来?你用的测量工具是什么?
(3)本题中需要测量哪些边长就可以算出旗杆的高度?
(4)你是利用什么知识来计算旗杆高度的?
通过上面的探究,你能设计出用这种方法测量旗杆高度的方案吗?
但是如果就你一个人,又遇上阴天,这种方法还能用吗?
探究二:利用测角仪测量旗杆的高度
如图25.1.2所示,站在离旗杆BE底部10米处的D点,目测旗杆的顶部,视线AB与水平线的夹角∠BAC为34°,并已知目高AD为1.5米.现在若按1∶500的比例将△ABC画在纸上,并记为△A′B′C′,用刻度直尺量出纸上B′C′的长度,便可以算出旗杆的实际高度.
你知道计算的方法吗?(提示:先测量出教材上图25.1.2中B′C′的长度)
学以致用: 知识链接 教材87页 习题25.1 1 2 3题
拓展提高:
探究三:利用标杆测量旗杆的高度
选一名同学做观测者,在观测者与旗杆之间的地面上直立一根高度适当的标杆,观测者适当调整自己所处的位置,当旗杆的顶部,标杆的顶端与眼睛恰好在一条直线上时,其他同学立即测出观测者的脚到旗杆底部的距离,以及观测者的脚到标杆底部的距离,然后,测得标杆的高,利用相似三角形相关知识计算。
探究四: 利用平面镜反射测量旗杆的高度
选一位同学作为观测者,在观测者与旗杆之间的地面上平放一面镜子,在镜子上做标记
观测者看着镜子来回移动,直至看到旗杆顶端在镜子上的标记重合,测数据,利用相似
三角形的判定及性质可求出旗杆的长。
应用提高:
设计一种方案,测量学校教学楼的高度。请写出测量的过程,并简要说明这样做的理由。
分析:测量大楼的高度的方法很多,现采用一种方法,利用人的身高和标杆,依据相似三角形三边对应成比例和平行线的性质,可测出大楼的高度。
解答:测量过程如下:
1、在地面上立一个标杆,使人眼、杆顶、楼顶在一条直线上。
2、测出CF、CH的距离。
大楼 3、算出KE的长度。
4、用标杆长度减去人的身高,即DE的长度。
标杆 5、由DE∥AB得△KDE∽△KAB。又因为相似三角形三边对应成比例,∴。
6、再将刚才测量的数值代入比例式中,计算出AB的长度。
7、用AB加上人的身高即得出大楼的高度。
探究点拔:1.选择测量的方法应是切实可行的。如本题中人眼、杆顶、楼顶在一条直线上(人是站立的)。
2.大楼的高度=AB+人高。
3.测量的过程要清楚,力求每步都有根有据,达到学以致用。
1.如图1,要测量A、B两点间距离,在O点设桩,取OA中点C, OB中点D,测得CD=31.4m 求AB长。 (AB=62.8m)
(2)
2. 如图2, 为了测量河的宽度,可以先在河对岸找到一个具有明显标志的点A,再在所在的一边找到两点B、C,使△ABC构成Rt△。如果测得BC=50米,∠ABC=73°,试设计一种方法求河的宽度AC。 (在地面上另作 Rt△A’B’C’,使B’C’=5米,∠C’=Rt∠,∠B’=73°, 测得 A’C’=16.35米,得 AC=16.35米 ).
