解直角三角形---方位角问题
图片预览

文档简介
课 题:《解直角三角形---方位角问题》
序 号: ( 9 )
年 级: 九年级 单元名称:第25章解直角三角形
课 型: 新授课 上课时间:
学习内容: 华东师大版 94---95页例2
学习目标:
1.使学生了解方位角的命名特点,能准确把握所指的方位角是指哪一个角
2.用三角函数有关知识解决方位角问题
重 点::用三角函数有关知识解决方位角问题
难 点:学会准确分析问题并将实际问题转化成数学模型
学法指导:合作探究
学 习 过 程
自主预习课本 94---95页例2,完成下列各题:
(1)小明家在学校的北偏东20°方向,那么学校在小明家的______方向。
(2)西北方向即北偏西_______度,东南方向即东偏南_____度,西南方向即南偏西______度,东北方向即东偏北_______度。
(3)小明从A点出发向东走100m,再沿北偏西30°方向走100m,那么小明在A点_________方向,距A点_________m。
探究一 方位角
1请同学们在练习本上画出方向图(表示东南西北四个方向的)。
2依次画出表示东南方向、西北方向、北偏东65度、南偏东34度方向的射线。
3根据你画的图,回答下列问题:
方位角是角吗?
角有哪些要素?
方位角具备这些要素吗?
我们通常以什么作为方位角的顶点?以什么作为方位角的边?
(5)什么是方位角?
4 方位角:指( )与( )的夹角。
注意:方位角通常是0----90的角。
(1)会认方位角:
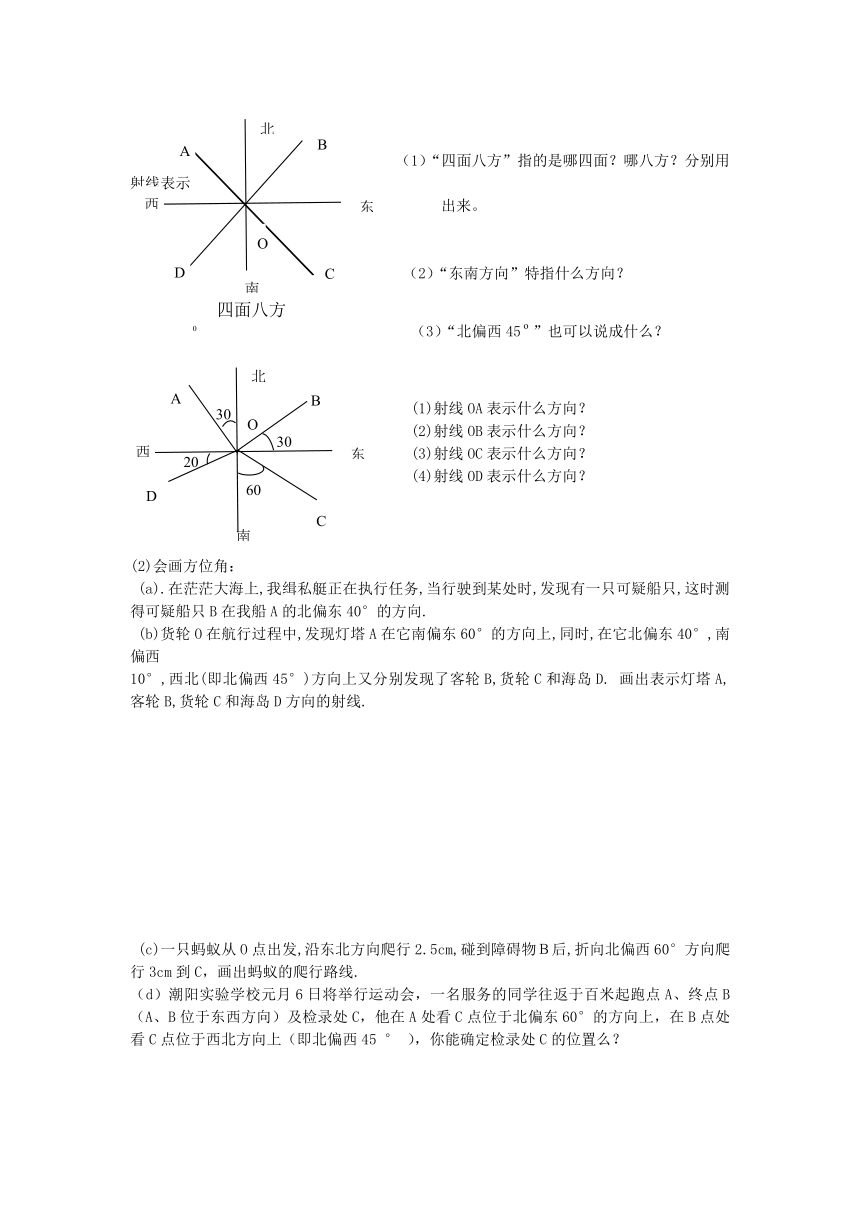
(1)“四面八方”指的是哪四面?哪八方?分别用射线表示
出来。
(2)“东南方向”特指什么方向?
(3)“北偏西45”也可以说成什么?
(1)射线OA表示什么方向?
(2)射线OB表示什么方向?
(3)射线OC表示什么方向?
(4)射线OD表示什么方向?
(2)会画方位角:
(a).在茫茫大海上,我缉私艇正在执行任务,当行驶到某处时,发现有一只可疑船只,这时测得可疑船只B在我船A的北偏东40°的方向.
(b)货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时,在它北偏东40°,南偏西
10°,西北(即北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D. 画出表示灯塔A,客轮B,货轮C和海岛D方向的射线.
(c)一只蚂蚁从O点出发,沿东北方向爬行2.5cm,碰到障碍物B后,折向北偏西60°方向爬行3cm到C,画出蚂蚁的爬行路线.
(d)潮阳实验学校元月6日将举行运动会,一名服务的同学往返于百米起跑点A、终点B(A、B位于东西方向)及检录处C,他在A处看C点位于北偏东60°的方向上,在B点处看C点位于西北方向上(即北偏西45 ° ),你能确定检录处C的位置么?
探究二 解决含有方位角的问题
问题1:某省将地处A、B的大学合并成一所综合性大学,为了方便两地师生的交往,学校准备在相距2km的A、B两地间修一条笔直的公路,经测量,在A地的北偏东60°方向,B地的北偏西45°方向的C处,有一个半径为0.7km的公园,问该公路是否穿过公园?为什么?
问题2:一艘货轮向正北方向航行,在点A处测得灯塔M在北偏西30°方向,货轮以20海里/小时的速度航行,1小时后到达B处,测得灯塔M在北偏西45°方向,问该货轮到达灯塔正东方向D处时,货轮与灯塔M的距离是多少?
跟踪练习:一渔船上的渔民在A处看见灯塔M在北偏东60°方向,这艘渔船以30海里/小时的速度向正东航行,半小时到B处,在B处看见灯塔M在北偏东15°方向,求灯塔M与渔船B的距离是多少?
问题3:如图,海岛A的周围8海里内有暗礁,鱼船跟踪鱼群由西向东航行,在点B处测得海岛A位于北偏东60°,航行12海里到达点C处,又测得海岛A位于北偏东30°,如果鱼船不改变航向继续向东航行.有没有触礁的危险?
1.某风景区的湖心岛有一凉亭A,其正东方向有一棵大树B,小明想测量A、B之间的距离,他从湖边的C处测得A在北偏西45°度方向上,测得B在北偏东32°方向上,且量得B、C之间距离为100m,求A、B之间的距离。
(结果精确到1m,sin32°≈0.53,cos32°≈0.85)
2上午10点整,一渔轮在小岛O的北偏东30°方向,距离等于10海里的A处,正以每小时10海里的速度向南偏东60°方向航行.那么渔轮到达小岛O的正东方向是什么时间?(精确到1分).
?
3如图,一艘海轮位于灯塔P的北偏东65方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34方向上的B处.这时,海轮所在的B处距离灯塔P有多远(精确到0.01海里)?
序 号: ( 9 )
年 级: 九年级 单元名称:第25章解直角三角形
课 型: 新授课 上课时间:
学习内容: 华东师大版 94---95页例2
学习目标:
1.使学生了解方位角的命名特点,能准确把握所指的方位角是指哪一个角
2.用三角函数有关知识解决方位角问题
重 点::用三角函数有关知识解决方位角问题
难 点:学会准确分析问题并将实际问题转化成数学模型
学法指导:合作探究
学 习 过 程
自主预习课本 94---95页例2,完成下列各题:
(1)小明家在学校的北偏东20°方向,那么学校在小明家的______方向。
(2)西北方向即北偏西_______度,东南方向即东偏南_____度,西南方向即南偏西______度,东北方向即东偏北_______度。
(3)小明从A点出发向东走100m,再沿北偏西30°方向走100m,那么小明在A点_________方向,距A点_________m。
探究一 方位角
1请同学们在练习本上画出方向图(表示东南西北四个方向的)。
2依次画出表示东南方向、西北方向、北偏东65度、南偏东34度方向的射线。
3根据你画的图,回答下列问题:
方位角是角吗?
角有哪些要素?
方位角具备这些要素吗?
我们通常以什么作为方位角的顶点?以什么作为方位角的边?
(5)什么是方位角?
4 方位角:指( )与( )的夹角。
注意:方位角通常是0----90的角。
(1)会认方位角:
(1)“四面八方”指的是哪四面?哪八方?分别用射线表示
出来。
(2)“东南方向”特指什么方向?
(3)“北偏西45”也可以说成什么?
(1)射线OA表示什么方向?
(2)射线OB表示什么方向?
(3)射线OC表示什么方向?
(4)射线OD表示什么方向?
(2)会画方位角:
(a).在茫茫大海上,我缉私艇正在执行任务,当行驶到某处时,发现有一只可疑船只,这时测得可疑船只B在我船A的北偏东40°的方向.
(b)货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时,在它北偏东40°,南偏西
10°,西北(即北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D. 画出表示灯塔A,客轮B,货轮C和海岛D方向的射线.
(c)一只蚂蚁从O点出发,沿东北方向爬行2.5cm,碰到障碍物B后,折向北偏西60°方向爬行3cm到C,画出蚂蚁的爬行路线.
(d)潮阳实验学校元月6日将举行运动会,一名服务的同学往返于百米起跑点A、终点B(A、B位于东西方向)及检录处C,他在A处看C点位于北偏东60°的方向上,在B点处看C点位于西北方向上(即北偏西45 ° ),你能确定检录处C的位置么?
探究二 解决含有方位角的问题
问题1:某省将地处A、B的大学合并成一所综合性大学,为了方便两地师生的交往,学校准备在相距2km的A、B两地间修一条笔直的公路,经测量,在A地的北偏东60°方向,B地的北偏西45°方向的C处,有一个半径为0.7km的公园,问该公路是否穿过公园?为什么?
问题2:一艘货轮向正北方向航行,在点A处测得灯塔M在北偏西30°方向,货轮以20海里/小时的速度航行,1小时后到达B处,测得灯塔M在北偏西45°方向,问该货轮到达灯塔正东方向D处时,货轮与灯塔M的距离是多少?
跟踪练习:一渔船上的渔民在A处看见灯塔M在北偏东60°方向,这艘渔船以30海里/小时的速度向正东航行,半小时到B处,在B处看见灯塔M在北偏东15°方向,求灯塔M与渔船B的距离是多少?
问题3:如图,海岛A的周围8海里内有暗礁,鱼船跟踪鱼群由西向东航行,在点B处测得海岛A位于北偏东60°,航行12海里到达点C处,又测得海岛A位于北偏东30°,如果鱼船不改变航向继续向东航行.有没有触礁的危险?
1.某风景区的湖心岛有一凉亭A,其正东方向有一棵大树B,小明想测量A、B之间的距离,他从湖边的C处测得A在北偏西45°度方向上,测得B在北偏东32°方向上,且量得B、C之间距离为100m,求A、B之间的距离。
(结果精确到1m,sin32°≈0.53,cos32°≈0.85)
2上午10点整,一渔轮在小岛O的北偏东30°方向,距离等于10海里的A处,正以每小时10海里的速度向南偏东60°方向航行.那么渔轮到达小岛O的正东方向是什么时间?(精确到1分).
?
3如图,一艘海轮位于灯塔P的北偏东65方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34方向上的B处.这时,海轮所在的B处距离灯塔P有多远(精确到0.01海里)?
