物理人教版(2019)选择性必修第一册2.2简谐运动的描述 (共25张ppt)
文档属性
| 名称 | 物理人教版(2019)选择性必修第一册2.2简谐运动的描述 (共25张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-09-05 21:52:56 | ||
图片预览


文档简介
(共25张PPT)
选择性必修一第二章
2.1 简谐运动
新课引入
思考:
做简谐运动的物体在一个位置附近不断地重复同样的运动。如何描述简谐运动的这种独特性呢?
思考
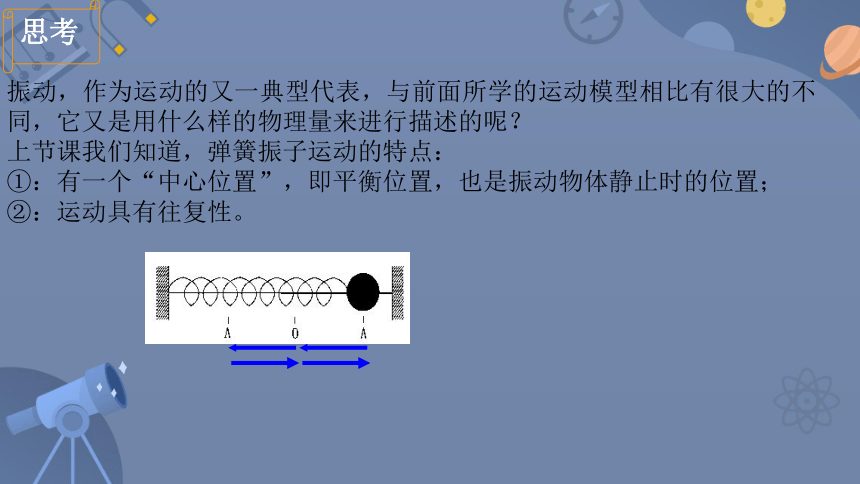
振动,作为运动的又一典型代表,与前面所学的运动模型相比有很大的不同,它又是用什么样的物理量来进行描述的呢?
上节课我们知道,弹簧振子运动的特点:
①:有一个“中心位置”,即平衡位置,也是振动物体静止时的位置;
②:运动具有往复性。
思考
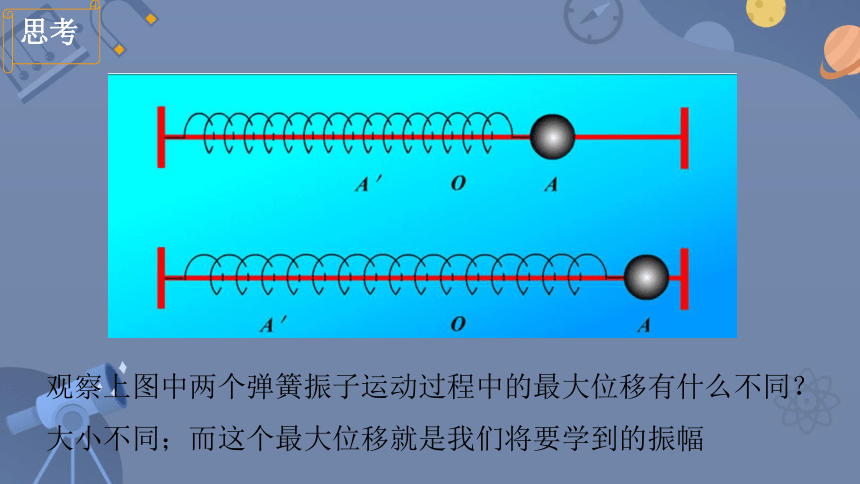
观察上图中两个弹簧振子运动过程中的最大位移有什么不同?
大小不同;而这个最大位移就是我们将要学到的振幅
机械振动
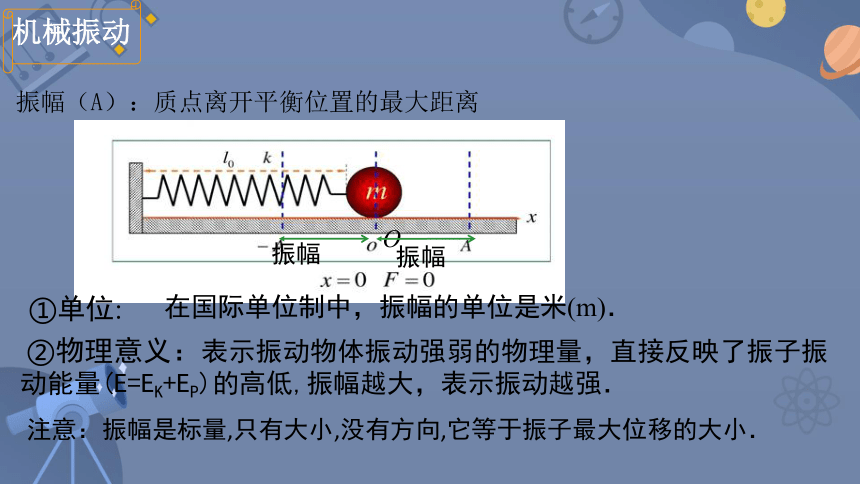
振幅(A):质点离开平衡位置的最大距离
振幅
振幅
O
①单位:
在国际单位制中,振幅的单位是米(m).
②物理意义:表示振动物体振动强弱的物理量,直接反映了振子振动能量(E=EK+EP)的高低,振幅越大,表示振动越强.
注意:振幅是标量,只有大小,没有方向,它等于振子最大位移的大小.
辨析
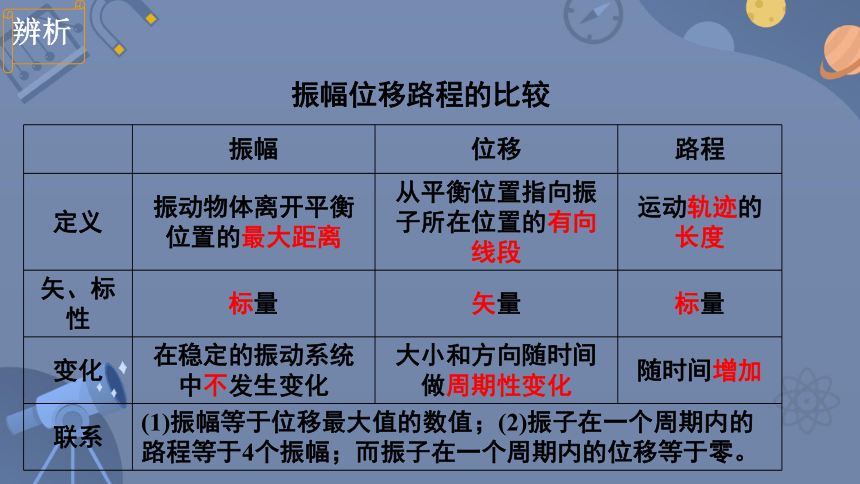
振幅 位移 路程
定义 振动物体离开平衡位置的最大距离 从平衡位置指向振子所在位置的有向线段 运动轨迹的长度
矢、标性 标量 矢量 标量
变化 在稳定的振动系统中不发生变化 大小和方向随时间做周期性变化 随时间增加
联系 (1)振幅等于位移最大值的数值;(2)振子在一个周期内的路程等于4个振幅;而振子在一个周期内的位移等于零。
振幅位移路程的比较
机械振动
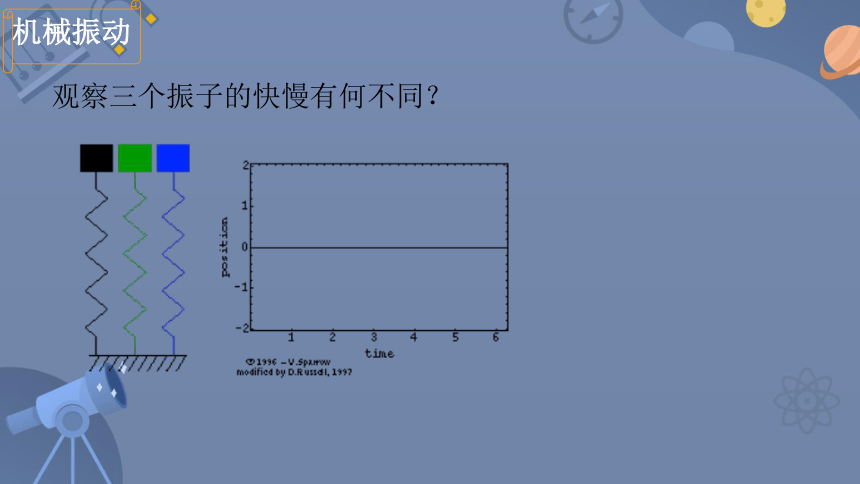
观察三个振子的快慢有何不同?
周期和频率
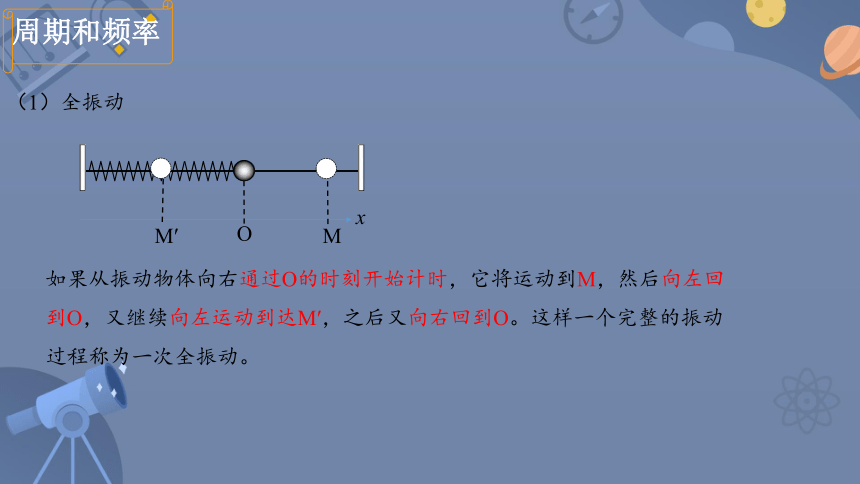
(1)全振动
M′
M
O
x
如果从振动物体向右通过O的时刻开始计时,它将运动到M,然后向左回到O,又继续向左运动到达M′,之后又向右回到O。这样一个完整的振动过程称为一次全振动。
周期和频率
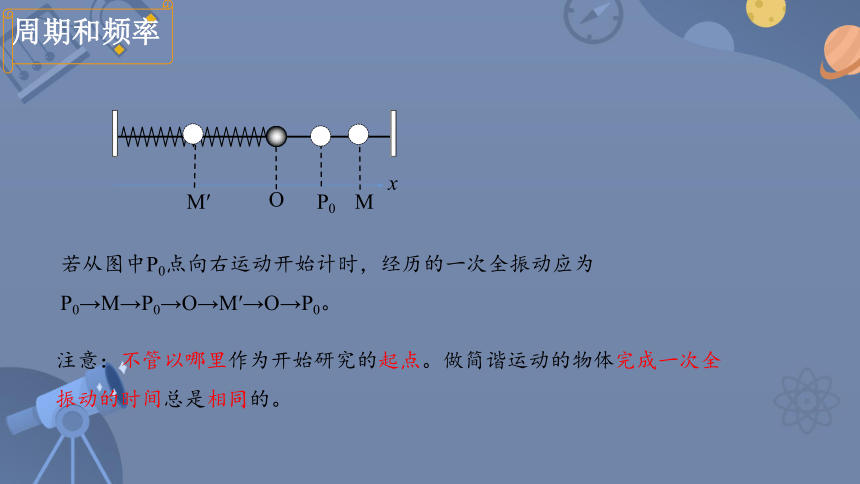
若从图中P0点向右运动开始计时,经历的一次全振动应为P0→M→P0→O→M′→O→P0。
M′
M
O
x
P0
注意:不管以哪里作为开始研究的起点。做简谐运动的物体完成一次全振动的时间总是相同的。
周期和频率
(2)周期:做简谐运动的物体完成一次全振动所需要的时间,叫作振动的周期。
(3)频率:单位时间内完成全振动的次数,用f表示,单位: Hz。
(4)周期T与频率f的关系:T=。
(5)物理意义:周期和频率都是表示物体振动快慢的物理量,周期越小,频率越大,表示物体振动越快。
(6)在国际单位制中,周期的单位是秒。频率的单位是赫兹,简称赫,符号是Hz。1 Hz=1s -1 。
周期和频率
实验探究:
周期和频率都反映振动快慢,那么它们与哪些因素有关呢?
测量小球振动的周期
如图弹簧上端固定,下端悬挂钢球。把钢球从平衡
位置向下拉一段距离 A,放手让其运动,A 就是振
动的振幅。用停表测出钢球完成 n 个全振动所用的
时间 t,nt 就是振动的周期。n 的值取大一些可以
减小测量误差。再把振幅减小为原来的一半,用同
样的方法测量振动的周期。
结论:弹簧振子的周期由振动系统本身的质量和劲度系数决定,而与振幅无关,所以常把周期和频率叫做固有周期和固有频率。
周期和频率
实验探究:
周期和频率都反映振动快慢,那么它们与哪些因素有关呢?
结论:弹簧振子的周期由振动系统本身的质量和劲度系数决定,而与振幅无关,所以常把周期和频率叫做固有周期和固有频率。
思考与讨论
弹簧振子在四分之一周期内的路程是一定是A吗?
A′
O
A
P
v
平衡位置
P ′
x
x
结论:
弹簧振子在一个周期内的路程一定是4A,半个周期内路程一定是2A,四分之一周期内的路程不一定是A。
简谐运动表达式
1.简谐运动的一般表达式
x=A sin(ωt+φ)
2.相位:
(ωt+φ)叫作相位;相位代表了做简谐运动的物体此时正处于一个运动周期中的哪个状态。
3. 初相:φ是t=0时的相位,称作初相位,或初相。
x1 = A2sin(t + 1 )
x2 = A2sin(t + 2 )
简谐运动表达式
3.相位差:Δφ = φ1 - φ2
如果两个简谐运动的频率相同,其初相分别是φ1和φ2,当φ1>φ2时,它们的相位差是Δφ = φ1 - φ2
①若,振动2的相位比1超前;
②若,振动2的相位比1落后。
实验探究
观察两个小球的振动情况
并列悬挂两个相同的弹簧振子。
(1)把小球向下拉同样的距离后同时放开。观察两球的振幅、周期、振动的步调。
(2)再次把两个小球拉到相同的位置,先把第一个小球放开,再放开第二个,观察两球的振幅、周期、振动的步调。
简谐运动
实验现象
(1)两个小球同时释放时,除了振幅和周期都相同外,还总是向同一方向运动,同时经过平衡位置,并同时到达同一侧的最大位移处。
(2)在一个周期内,如果不同时释放小球,它们的步调就不一致。
简谐运动
同相、反相
4.同相和反相
(1)同相:相位差为零,一般地为 =2n (n=0,1,2,……)。振动步调完全相同。
A与B同相
(2)反相:相位差为 ,一般地为 =(2n+1) (n=0,1,2,……)。振动步调完全相反。
A与C反相
摩擦起电演示图:
典型例题
例1.一列简谐横波沿x轴正方向传播,传播的速度大小为4.0m/s,t=0时刻的波形图如图所示。则t=0时刻x=9m处的质点沿y轴 (填“正方向”或“负方向”)振动,x=11m处的质点比x=1m处的质点振动滞后 s,从到时间内处质点通过的路程为 m。
正方向
2.5
2
摩擦起电演示图:
典型例题
例2.一质点做简谐运动的图象如图所示,下列说法正确的是( )
A.质点振动频率是4 Hz
B.在10 s内质点经过的路程是20 cm
C.第4 s末质点的速度为零
D.t=1 s和t=3 s两时刻,质点位移大小相等,方向相同
B
摩擦起电演示图:
典型例题
例3.某弹簧振子沿x轴的简谐运动图象如图所示,下列描述正确的是( )
A.t =1 s时,振子的速度为零,加速度为负的最大值
B.t =2 s时,振子的速度为负,加速度为正的最大值
C.t =3 s时,振子的速度为负的最大值,加速度为零
D.t =4 s时,振子的速度为正,加速度为负的最大值
A
摩擦起电演示图:
典型例题
例4.一弹簧振子做简谐运动的振动图象如图所示,已知弹簧的劲度系数为20N/cm,则( )
A.图中A点对应的时刻振子所受的弹力大小为5N,方向指向轴的负方向
B.图中A点对应的时刻振子的速度方向指向轴的正方向
C.在0~4s内振子做了1.75次全振动
D.在0~4s内振子通过的路程为3.5cm,位移为0
AB
摩擦起电演示图:
典型例题
例5.一物体沿x轴做简谐运动,振幅为8 cm,频率为0.5 Hz,在t=0时,位移是4 cm,且向x轴负方向运动,试写出用正弦函数表示的振动方程,并画出相应的振动图像。
解析:简谐运动的表达式为x=Asin(ωt+φ),根据题目所给条件得A=8 cm,ω=2πf=π,所以x=8sin(πt+φ) cm,将t=0,x0=4 cm代入得4=8sin φ,解得初相φ=或φ=π,因为t=0时,速度方向沿x轴负方向,即位移在减小,所以取φ=π,所求的振动方程为x=8sin(πt+π) cm,画对应的振动图像如图所示:
摩擦起电演示图:
课堂小结
简谐运动的描述
描述简谐运动的物理量
周期T:表示振动快慢
振幅A:表示振动强弱
简谐运动的表达式x=Asin(ωt+φ)
频率f
相位φ:表示振动状态
感谢您的观看
选择性必修一第二章
2.1 简谐运动
新课引入
思考:
做简谐运动的物体在一个位置附近不断地重复同样的运动。如何描述简谐运动的这种独特性呢?
思考
振动,作为运动的又一典型代表,与前面所学的运动模型相比有很大的不同,它又是用什么样的物理量来进行描述的呢?
上节课我们知道,弹簧振子运动的特点:
①:有一个“中心位置”,即平衡位置,也是振动物体静止时的位置;
②:运动具有往复性。
思考
观察上图中两个弹簧振子运动过程中的最大位移有什么不同?
大小不同;而这个最大位移就是我们将要学到的振幅
机械振动
振幅(A):质点离开平衡位置的最大距离
振幅
振幅
O
①单位:
在国际单位制中,振幅的单位是米(m).
②物理意义:表示振动物体振动强弱的物理量,直接反映了振子振动能量(E=EK+EP)的高低,振幅越大,表示振动越强.
注意:振幅是标量,只有大小,没有方向,它等于振子最大位移的大小.
辨析
振幅 位移 路程
定义 振动物体离开平衡位置的最大距离 从平衡位置指向振子所在位置的有向线段 运动轨迹的长度
矢、标性 标量 矢量 标量
变化 在稳定的振动系统中不发生变化 大小和方向随时间做周期性变化 随时间增加
联系 (1)振幅等于位移最大值的数值;(2)振子在一个周期内的路程等于4个振幅;而振子在一个周期内的位移等于零。
振幅位移路程的比较
机械振动
观察三个振子的快慢有何不同?
周期和频率
(1)全振动
M′
M
O
x
如果从振动物体向右通过O的时刻开始计时,它将运动到M,然后向左回到O,又继续向左运动到达M′,之后又向右回到O。这样一个完整的振动过程称为一次全振动。
周期和频率
若从图中P0点向右运动开始计时,经历的一次全振动应为P0→M→P0→O→M′→O→P0。
M′
M
O
x
P0
注意:不管以哪里作为开始研究的起点。做简谐运动的物体完成一次全振动的时间总是相同的。
周期和频率
(2)周期:做简谐运动的物体完成一次全振动所需要的时间,叫作振动的周期。
(3)频率:单位时间内完成全振动的次数,用f表示,单位: Hz。
(4)周期T与频率f的关系:T=。
(5)物理意义:周期和频率都是表示物体振动快慢的物理量,周期越小,频率越大,表示物体振动越快。
(6)在国际单位制中,周期的单位是秒。频率的单位是赫兹,简称赫,符号是Hz。1 Hz=1s -1 。
周期和频率
实验探究:
周期和频率都反映振动快慢,那么它们与哪些因素有关呢?
测量小球振动的周期
如图弹簧上端固定,下端悬挂钢球。把钢球从平衡
位置向下拉一段距离 A,放手让其运动,A 就是振
动的振幅。用停表测出钢球完成 n 个全振动所用的
时间 t,nt 就是振动的周期。n 的值取大一些可以
减小测量误差。再把振幅减小为原来的一半,用同
样的方法测量振动的周期。
结论:弹簧振子的周期由振动系统本身的质量和劲度系数决定,而与振幅无关,所以常把周期和频率叫做固有周期和固有频率。
周期和频率
实验探究:
周期和频率都反映振动快慢,那么它们与哪些因素有关呢?
结论:弹簧振子的周期由振动系统本身的质量和劲度系数决定,而与振幅无关,所以常把周期和频率叫做固有周期和固有频率。
思考与讨论
弹簧振子在四分之一周期内的路程是一定是A吗?
A′
O
A
P
v
平衡位置
P ′
x
x
结论:
弹簧振子在一个周期内的路程一定是4A,半个周期内路程一定是2A,四分之一周期内的路程不一定是A。
简谐运动表达式
1.简谐运动的一般表达式
x=A sin(ωt+φ)
2.相位:
(ωt+φ)叫作相位;相位代表了做简谐运动的物体此时正处于一个运动周期中的哪个状态。
3. 初相:φ是t=0时的相位,称作初相位,或初相。
x1 = A2sin(t + 1 )
x2 = A2sin(t + 2 )
简谐运动表达式
3.相位差:Δφ = φ1 - φ2
如果两个简谐运动的频率相同,其初相分别是φ1和φ2,当φ1>φ2时,它们的相位差是Δφ = φ1 - φ2
①若,振动2的相位比1超前;
②若,振动2的相位比1落后。
实验探究
观察两个小球的振动情况
并列悬挂两个相同的弹簧振子。
(1)把小球向下拉同样的距离后同时放开。观察两球的振幅、周期、振动的步调。
(2)再次把两个小球拉到相同的位置,先把第一个小球放开,再放开第二个,观察两球的振幅、周期、振动的步调。
简谐运动
实验现象
(1)两个小球同时释放时,除了振幅和周期都相同外,还总是向同一方向运动,同时经过平衡位置,并同时到达同一侧的最大位移处。
(2)在一个周期内,如果不同时释放小球,它们的步调就不一致。
简谐运动
同相、反相
4.同相和反相
(1)同相:相位差为零,一般地为 =2n (n=0,1,2,……)。振动步调完全相同。
A与B同相
(2)反相:相位差为 ,一般地为 =(2n+1) (n=0,1,2,……)。振动步调完全相反。
A与C反相
摩擦起电演示图:
典型例题
例1.一列简谐横波沿x轴正方向传播,传播的速度大小为4.0m/s,t=0时刻的波形图如图所示。则t=0时刻x=9m处的质点沿y轴 (填“正方向”或“负方向”)振动,x=11m处的质点比x=1m处的质点振动滞后 s,从到时间内处质点通过的路程为 m。
正方向
2.5
2
摩擦起电演示图:
典型例题
例2.一质点做简谐运动的图象如图所示,下列说法正确的是( )
A.质点振动频率是4 Hz
B.在10 s内质点经过的路程是20 cm
C.第4 s末质点的速度为零
D.t=1 s和t=3 s两时刻,质点位移大小相等,方向相同
B
摩擦起电演示图:
典型例题
例3.某弹簧振子沿x轴的简谐运动图象如图所示,下列描述正确的是( )
A.t =1 s时,振子的速度为零,加速度为负的最大值
B.t =2 s时,振子的速度为负,加速度为正的最大值
C.t =3 s时,振子的速度为负的最大值,加速度为零
D.t =4 s时,振子的速度为正,加速度为负的最大值
A
摩擦起电演示图:
典型例题
例4.一弹簧振子做简谐运动的振动图象如图所示,已知弹簧的劲度系数为20N/cm,则( )
A.图中A点对应的时刻振子所受的弹力大小为5N,方向指向轴的负方向
B.图中A点对应的时刻振子的速度方向指向轴的正方向
C.在0~4s内振子做了1.75次全振动
D.在0~4s内振子通过的路程为3.5cm,位移为0
AB
摩擦起电演示图:
典型例题
例5.一物体沿x轴做简谐运动,振幅为8 cm,频率为0.5 Hz,在t=0时,位移是4 cm,且向x轴负方向运动,试写出用正弦函数表示的振动方程,并画出相应的振动图像。
解析:简谐运动的表达式为x=Asin(ωt+φ),根据题目所给条件得A=8 cm,ω=2πf=π,所以x=8sin(πt+φ) cm,将t=0,x0=4 cm代入得4=8sin φ,解得初相φ=或φ=π,因为t=0时,速度方向沿x轴负方向,即位移在减小,所以取φ=π,所求的振动方程为x=8sin(πt+π) cm,画对应的振动图像如图所示:
摩擦起电演示图:
课堂小结
简谐运动的描述
描述简谐运动的物理量
周期T:表示振动快慢
振幅A:表示振动强弱
简谐运动的表达式x=Asin(ωt+φ)
频率f
相位φ:表示振动状态
感谢您的观看
