相似三角形的判定(二)
图片预览

文档简介
课 题:相似三角形的判定(二)
序 号: ( 7 )
年 级: 九年级 单元名称:第24章相似图形的性质
课 型: 新授课 上课时间:
学习内容:华东师大版课本55----59页
学习目标:1.能熟记相似三角形的三种判定方法。
2.会灵活选用适当的方法来判断两个三角形相似。
重 点:会灵活选用适当的方法来判断两个三角形相似。
难 点:会灵活选用适当的方法来判断两个三角形相似。
学法指导:合作探究
学 习 过 程
判定三角形相似的方法有哪些?并用几何语言表示出来。
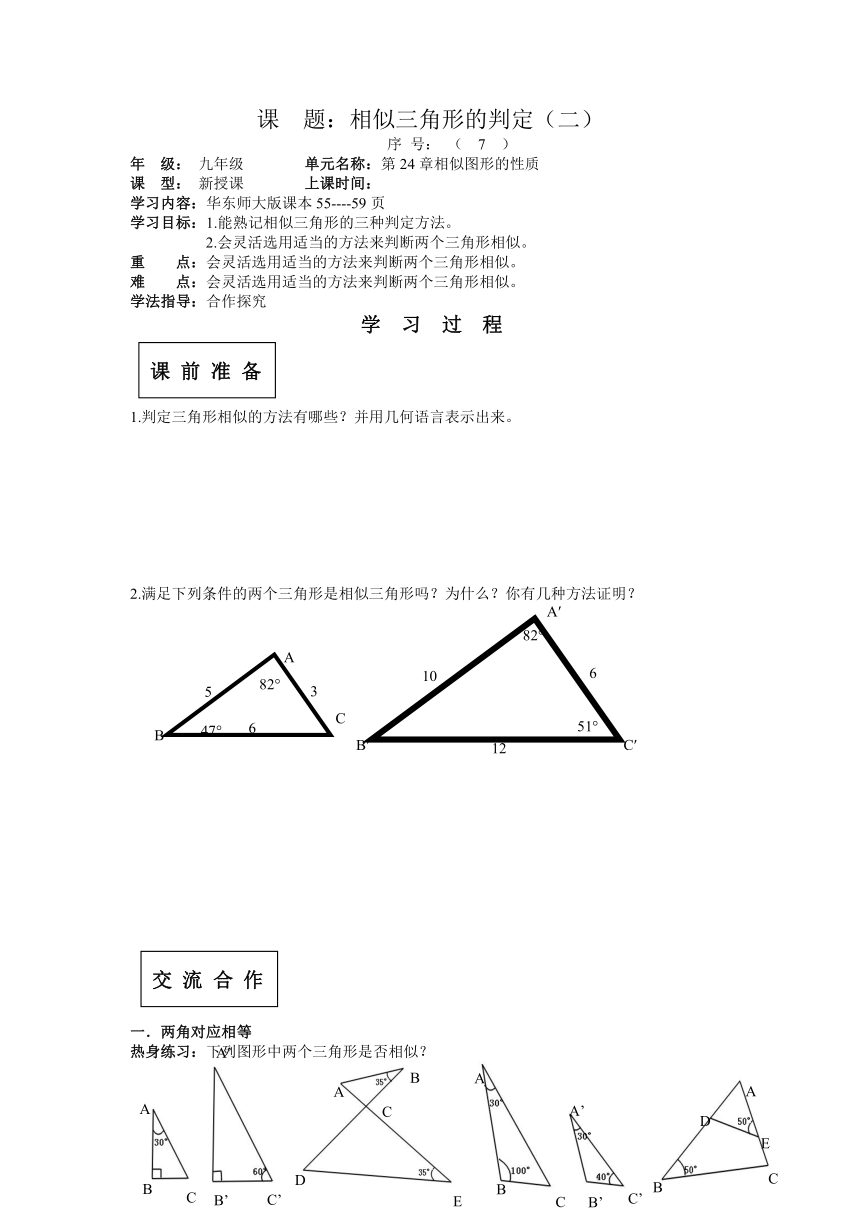
2.满足下列条件的两个三角形是相似三角形吗?为什么?你有几种方法证明?
一.两角对应相等
热身练习:下列图形中两个三角形是否相似?
学以致用1:如图,△ABC中,DE∥BC,EF∥AB,证明:△ADE∽△EFC.
跟踪练习:如图,E、F分别是△ABC的边BC上的点,DE∥AB,DF∥AC , 求证:△ABC∽△DEF。
学以致用2:如图所示,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D,交AB于点M,有下面4个结论:
射线BD是∠ABC的角平分线; ②△BCD是等腰三角形;
③ △ABC∽△BCD; ④ △ADE≌△BCD。
(1)判断其中正确的结论是哪几个?
(2)从你认为是正确的结论中选一个加以证明?
学以致用3:已知:如图,∠1=∠2=∠3,求证:△ABC∽△ADE.
学以致用4:如图所示,已知在正方形ABCD中,P是BC上一点,连结AP,作AP⊥PQ交CD于Q
(1)求证:△ABP∽△PCQ;(2)求证:;(3)若AB=2,BP=,求CQ。
二:两边夹角
学以致用1:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点.ΔADQ与
ΔQCP是否相似?为什么?
学以致用2:△ABC中,点D在AB上,如果AC2=AD AB,
那么△ACD与△ABC相似吗?说说你的理由.
跟踪练习:已知:如图,P为△ABC中线AD上的一点,且
求证:△ADC∽△CDP.
三:三边成比例
如图,△ABC中,点D、E、F分别是AB、BC、CA的中点,
求证:△ABC∽△DEF.
四.综合应用:
1.已知,如图1要△ABC∽△ACD,需要条件 ;
2.已知,如图2要使△ABE∽△ACD ,需要条件 ;
图1 图2
3.如图,D是△ABC的边AC 上一点,连接BD,△ABC∽△BDC,则需要添加的条件是 。
1.(选择)如图,DE∥BC,EF∥AB,则图中相似三角形一共有( )
A.1对 B.2对 C.3对 D.4对
2.已知:如图,AB∥EF ∥CD,图中共有______对相似三角形。
3.如图,在△ABC中,DG∥EH∥FI∥BC,
(1)请找出图中所有的相似三角形;
(2)如果AD=1,DB=3,那么DG:BC=_________。
4.如图,AB AC=AD AE,且∠1=∠2,求证:△ABC∽△AED。
课 前 准 备
A′
B′
C′
10
6
12
51°
82°
C
A
B
5
3
82°
47°
6
交 流 合 作
B
C
A
A’
C’
B’
A
B
C
D
E
A
B
C
A’
B’
C’
A
B
C
D
E
A
B
C
D
E
F
D
M
C
A
N
B
A
D
B
C
P
Q
课 后 反 思
A
第3题
D
C
B
达 标 检 测
A
B
C
D
E
F
G
H
I
序 号: ( 7 )
年 级: 九年级 单元名称:第24章相似图形的性质
课 型: 新授课 上课时间:
学习内容:华东师大版课本55----59页
学习目标:1.能熟记相似三角形的三种判定方法。
2.会灵活选用适当的方法来判断两个三角形相似。
重 点:会灵活选用适当的方法来判断两个三角形相似。
难 点:会灵活选用适当的方法来判断两个三角形相似。
学法指导:合作探究
学 习 过 程
判定三角形相似的方法有哪些?并用几何语言表示出来。
2.满足下列条件的两个三角形是相似三角形吗?为什么?你有几种方法证明?
一.两角对应相等
热身练习:下列图形中两个三角形是否相似?
学以致用1:如图,△ABC中,DE∥BC,EF∥AB,证明:△ADE∽△EFC.
跟踪练习:如图,E、F分别是△ABC的边BC上的点,DE∥AB,DF∥AC , 求证:△ABC∽△DEF。
学以致用2:如图所示,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D,交AB于点M,有下面4个结论:
射线BD是∠ABC的角平分线; ②△BCD是等腰三角形;
③ △ABC∽△BCD; ④ △ADE≌△BCD。
(1)判断其中正确的结论是哪几个?
(2)从你认为是正确的结论中选一个加以证明?
学以致用3:已知:如图,∠1=∠2=∠3,求证:△ABC∽△ADE.
学以致用4:如图所示,已知在正方形ABCD中,P是BC上一点,连结AP,作AP⊥PQ交CD于Q
(1)求证:△ABP∽△PCQ;(2)求证:;(3)若AB=2,BP=,求CQ。
二:两边夹角
学以致用1:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点.ΔADQ与
ΔQCP是否相似?为什么?
学以致用2:△ABC中,点D在AB上,如果AC2=AD AB,
那么△ACD与△ABC相似吗?说说你的理由.
跟踪练习:已知:如图,P为△ABC中线AD上的一点,且
求证:△ADC∽△CDP.
三:三边成比例
如图,△ABC中,点D、E、F分别是AB、BC、CA的中点,
求证:△ABC∽△DEF.
四.综合应用:
1.已知,如图1要△ABC∽△ACD,需要条件 ;
2.已知,如图2要使△ABE∽△ACD ,需要条件 ;
图1 图2
3.如图,D是△ABC的边AC 上一点,连接BD,△ABC∽△BDC,则需要添加的条件是 。
1.(选择)如图,DE∥BC,EF∥AB,则图中相似三角形一共有( )
A.1对 B.2对 C.3对 D.4对
2.已知:如图,AB∥EF ∥CD,图中共有______对相似三角形。
3.如图,在△ABC中,DG∥EH∥FI∥BC,
(1)请找出图中所有的相似三角形;
(2)如果AD=1,DB=3,那么DG:BC=_________。
4.如图,AB AC=AD AE,且∠1=∠2,求证:△ABC∽△AED。
课 前 准 备
A′
B′
C′
10
6
12
51°
82°
C
A
B
5
3
82°
47°
6
交 流 合 作
B
C
A
A’
C’
B’
A
B
C
D
E
A
B
C
A’
B’
C’
A
B
C
D
E
A
B
C
D
E
F
D
M
C
A
N
B
A
D
B
C
P
Q
课 后 反 思
A
第3题
D
C
B
达 标 检 测
A
B
C
D
E
F
G
H
I
