物理人教版2019选择性必修第一册2.4 单摆(共21张ppt)
文档属性
| 名称 | 物理人教版2019选择性必修第一册2.4 单摆(共21张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-09-05 22:01:51 | ||
图片预览



文档简介
(共21张PPT)
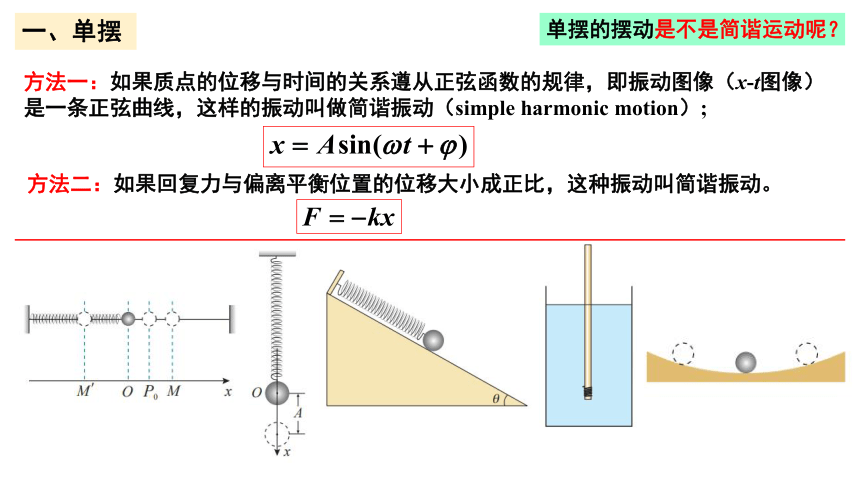
第二章 机械振动
2.4 单摆
simple pendulum
生活中经常可以看到悬挂起来的物体在竖直平面内往复运动。将一小球用细绳悬挂起来,把小球拉离最低点释放后,小球就会来回摆动。小球的摆动是否为简谐运动呢?
生活问题
一、单摆
如果细线的长度不可改变,细线的质量与小球相比可以忽略,球的直径与线的长度相比也可以忽略,这样的装置就叫作单摆(simple pendulum)。
简化处理:与小球受到的重力及绳的拉力相比,空气等对它的阻力可以忽略。
单摆是实际摆的理想化模型。
单摆摆动时摆球在做振动,是不是简谐运动呢?
实验时要尽量选择质量大、体积小的球和尽量细的线。
(1)忽略线的伸缩和质量;
(2)线长远大于球的直径;
(3)振动时空气阻力可以忽略;
一、单摆
单摆的摆动是不是简谐运动呢?
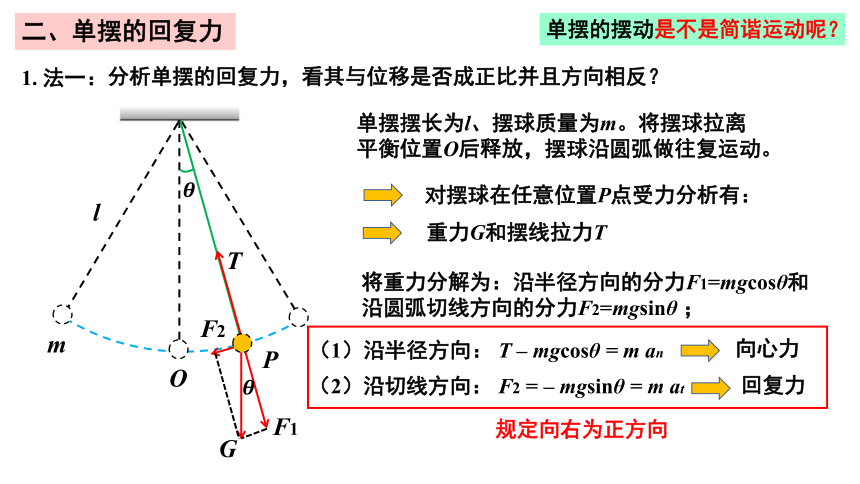
方法二:如果回复力与偏离平衡位置的位移大小成正比,这种振动叫简谐振动。
方法一:如果质点的位移与时间的关系遵从正弦函数的规律,即振动图像(x-t图像)是一条正弦曲线,这样的振动叫做简谐振动(simple harmonic motion);
单摆的摆动是不是简谐运动呢?
1. 法一:
分析单摆的回复力,看其与位移是否成正比并且方向相反?
二、单摆的回复力
单摆摆长为l、摆球质量为m。将摆球拉离平衡位置O后释放,摆球沿圆弧做往复运动。
对摆球在任意位置P点受力分析有:
l
m
O
G
P
F1
F2
T
重力G和摆线拉力T
将重力分解为:沿半径方向的分力F1=mgcosθ和沿圆弧切线方向的分力F2=mgsinθ ;
(1)沿半径方向: T – mgcosθ = m an
(2)沿切线方向: F2 = – mgsinθ = m at
向心力
回复力
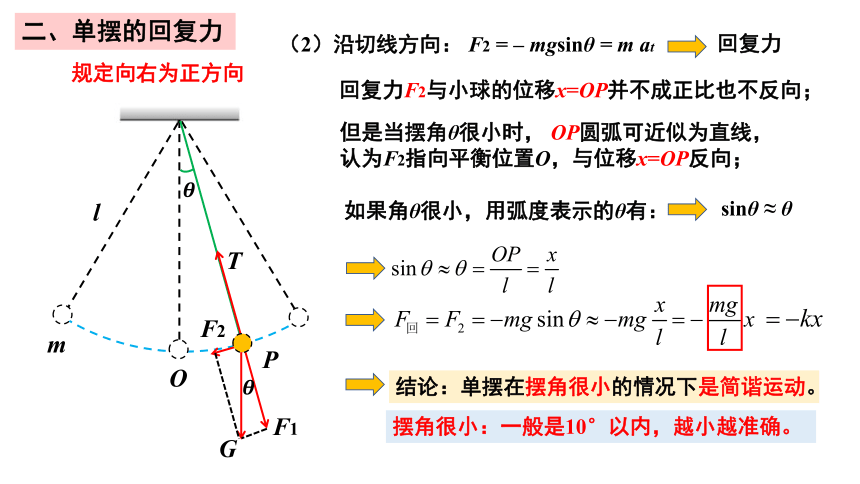
规定向右为正方向
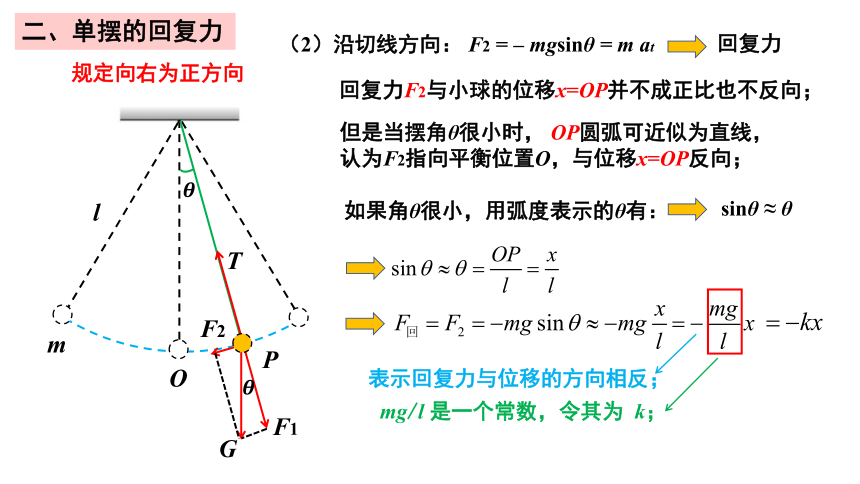
回复力F2与小球的位移x=OP并不成正比也不反向;
二、单摆的回复力
但是当摆角θ很小时, OP圆弧可近似为直线,认为F2指向平衡位置O,与位移x=OP反向;
(2)沿切线方向: F2 = – mgsinθ = m at
回复力
l
m
O
G
P
F1
F2
T
规定向右为正方向
如果角θ很小,用弧度表示的θ有:
sinθ ≈ θ
表示回复力与位移的方向相反;
mg/l 是一个常数,令其为 k;
回复力F2与小球的位移x=OP并不成正比也不反向;
二、单摆的回复力
但是当摆角θ很小时, OP圆弧可近似为直线,认为F2指向平衡位置O,与位移x=OP反向;
回复力
l
m
O
G
P
F1
F2
T
规定向右为正方向
如果角θ很小,用弧度表示的θ有:
sinθ ≈ θ
结论:单摆在摆角很小的情况下是简谐运动。
(2)沿切线方向: F2 = – mgsinθ = m at
摆角很小:一般是10°以内,越小越准确。
单摆的摆动是不是简谐运动呢?
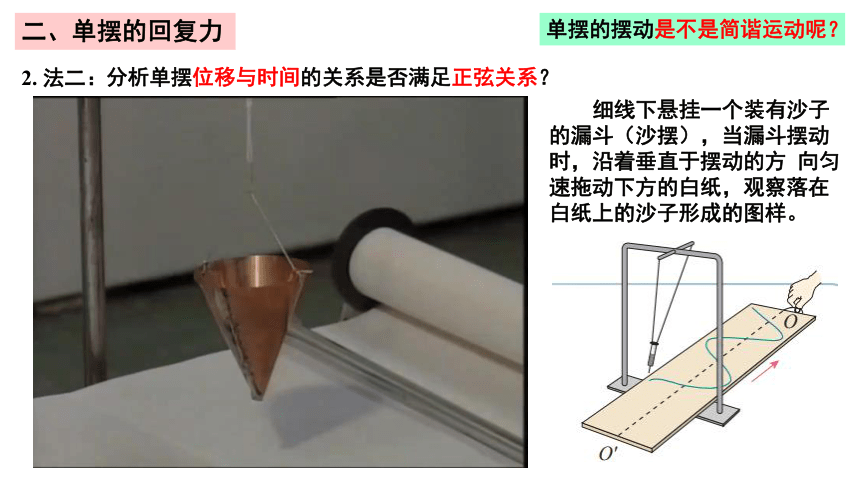
2. 法二:
分析单摆位移与时间的关系是否满足正弦关系?
细线下悬挂一个装有沙子的漏斗(沙摆),当漏斗摆动时,沿着垂直于摆动的方 向匀速拖动下方的白纸,观察落在白纸上的沙子形成的图样。
二、单摆的回复力
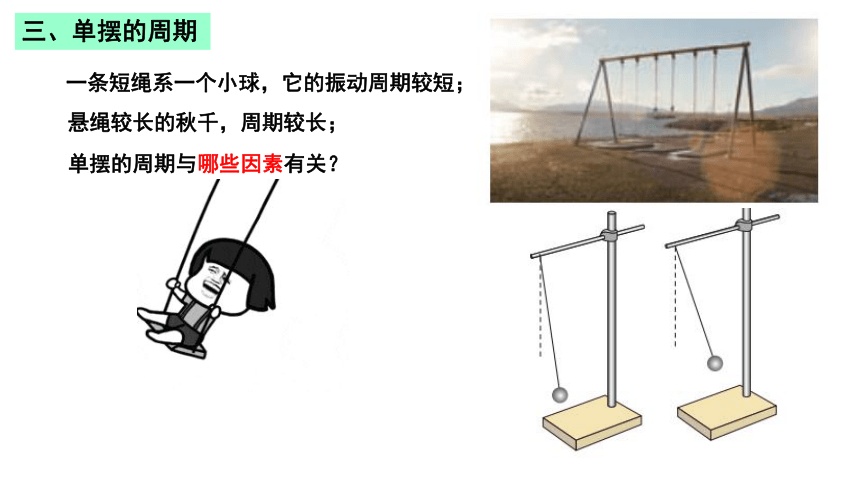
三、单摆的周期
一条短绳系一个小球,它的振动周期较短;
悬绳较长的秋千,周期较长;
单摆的周期与哪些因素有关?
三、单摆的周期
探究单摆周期与摆长之间的关系
在铁架台的横梁上固定两个单摆,按照以下几种情况,把它们拉起一定的小角度后同时释放,观察两摆的振动周期。
1. 摆球质量、摆长相同,振幅不同(都在小偏角下);
周期近似相等。
三、单摆的周期
在铁架台的横梁上固定两个单摆,按照以下几种情况,把它们拉起一定的小角度后同时释放,观察两摆的振动周期。
2. 摆长、振幅相同,摆球质量不同;
周期近似相等。
探究单摆周期与摆长之间的关系
三、单摆的周期
3. 两摆的振幅、摆球质量相同,摆长不同。
周期不相等。
探究单摆周期与摆长之间的关系
三、单摆的周期
在铁架台的横梁上固定两个单摆,按照以下几种情况,把它们拉起一定的小角度后同时释放,观察两摆的振动周期。
综上所述:
实验表明:单摆做简谐运动的周期与摆长有关,摆长越长,周期越大;单摆的周期与摆球质量和振幅无关。
探究单摆周期与摆长之间的关系
三、单摆的周期
为了找出定量的关系,荷兰物理学家惠更斯进行了详尽的研究,发现单摆做简谐运动的周期T与摆长l的二次方根成正比,与重力加速度g的二次方根成反比,而与振幅、摆球质量无关。
惠更斯确定了计算单摆周期的公式(单摆定律):
单摆周期公式的发现,为人类利用简谐运动定量计时提供了可能,并以此为基础发明了真正可持续运转的时钟。
摆钟是一种时钟,由荷兰物理学家惠更斯(Huygens)发明于1656年,根据单摆定律制造,用摆锤控制其它机件,使钟走的快慢均匀,一般能报点,要用发条来提供能量使其摆动。
探究单摆周期与摆长之间的关系
简谐运动与圆的故事
四、有趣的事情…
有趣的是:
绿色小球做匀速周周运动一圈
红色振子做简谐运动一个周期
匀速圆周运动和简谐运动肯定有着密切的联系
有趣的事发生了…
小球和振子任意时刻均在同一竖直线上
简谐运动与圆的故事
质点在x轴上投影的运动是简谐振动
绿球的向心力的水平分力:
则:
红球的回复力:
简谐振动的周期与周圆运动的周期相同
(具有普遍性,对所有的简谐运动都适用)
简谐振动的位移随时间变化:
四、有趣的事情…
w
O
x
A
回到单摆
具有普遍性,
对所有的简谐运动都适用
四、有趣的事情…
l
m
O
G
P
F1
F2
T
规定向右为正方向
结论:单摆在摆角很小的情况下是简谐运动。
单摆:
五、练习与应用
1. 探究单摆周期与摆长之间的一个理想单摆,已知其周期为T。如果由于某种原因(如转移到其他星球)自由落体加速度变为原来的1/2 ,振幅变为原来的1/3,摆长变为原来的1/4,摆球的质量变为原来的1/5,它的周期变为多少?
五、练习与应用
2. 周期是2s的单摆叫秒摆,秒摆的摆长是多少?把一个地球上的秒摆拿到月球上去,已知月球上的自由落体加速度为1.6 m/s2,它在月球上做50次全振动要用多少时间?
五、练习与应用
3. 如图是两个单摆的振动图像。
(1)甲、乙两个摆的摆长之比是多少?
(2)以向右的方向作为摆球偏离平衡位置的位移的正方向,从t=0起,乙第一次到达右方最大位移时,甲摆动到了什么位置?向什么方向运动?
五、练习与应用
4. 一条细线下面挂着一个小球,让它自由摆动,画出它的振动图像如图所示。
(1)请根据图中的数据计算出它的摆长。
(2)请根据图中的数据估算出它摆动的最大偏角。
第二章 机械振动
2.4 单摆
simple pendulum
生活中经常可以看到悬挂起来的物体在竖直平面内往复运动。将一小球用细绳悬挂起来,把小球拉离最低点释放后,小球就会来回摆动。小球的摆动是否为简谐运动呢?
生活问题
一、单摆
如果细线的长度不可改变,细线的质量与小球相比可以忽略,球的直径与线的长度相比也可以忽略,这样的装置就叫作单摆(simple pendulum)。
简化处理:与小球受到的重力及绳的拉力相比,空气等对它的阻力可以忽略。
单摆是实际摆的理想化模型。
单摆摆动时摆球在做振动,是不是简谐运动呢?
实验时要尽量选择质量大、体积小的球和尽量细的线。
(1)忽略线的伸缩和质量;
(2)线长远大于球的直径;
(3)振动时空气阻力可以忽略;
一、单摆
单摆的摆动是不是简谐运动呢?
方法二:如果回复力与偏离平衡位置的位移大小成正比,这种振动叫简谐振动。
方法一:如果质点的位移与时间的关系遵从正弦函数的规律,即振动图像(x-t图像)是一条正弦曲线,这样的振动叫做简谐振动(simple harmonic motion);
单摆的摆动是不是简谐运动呢?
1. 法一:
分析单摆的回复力,看其与位移是否成正比并且方向相反?
二、单摆的回复力
单摆摆长为l、摆球质量为m。将摆球拉离平衡位置O后释放,摆球沿圆弧做往复运动。
对摆球在任意位置P点受力分析有:
l
m
O
G
P
F1
F2
T
重力G和摆线拉力T
将重力分解为:沿半径方向的分力F1=mgcosθ和沿圆弧切线方向的分力F2=mgsinθ ;
(1)沿半径方向: T – mgcosθ = m an
(2)沿切线方向: F2 = – mgsinθ = m at
向心力
回复力
规定向右为正方向
回复力F2与小球的位移x=OP并不成正比也不反向;
二、单摆的回复力
但是当摆角θ很小时, OP圆弧可近似为直线,认为F2指向平衡位置O,与位移x=OP反向;
(2)沿切线方向: F2 = – mgsinθ = m at
回复力
l
m
O
G
P
F1
F2
T
规定向右为正方向
如果角θ很小,用弧度表示的θ有:
sinθ ≈ θ
表示回复力与位移的方向相反;
mg/l 是一个常数,令其为 k;
回复力F2与小球的位移x=OP并不成正比也不反向;
二、单摆的回复力
但是当摆角θ很小时, OP圆弧可近似为直线,认为F2指向平衡位置O,与位移x=OP反向;
回复力
l
m
O
G
P
F1
F2
T
规定向右为正方向
如果角θ很小,用弧度表示的θ有:
sinθ ≈ θ
结论:单摆在摆角很小的情况下是简谐运动。
(2)沿切线方向: F2 = – mgsinθ = m at
摆角很小:一般是10°以内,越小越准确。
单摆的摆动是不是简谐运动呢?
2. 法二:
分析单摆位移与时间的关系是否满足正弦关系?
细线下悬挂一个装有沙子的漏斗(沙摆),当漏斗摆动时,沿着垂直于摆动的方 向匀速拖动下方的白纸,观察落在白纸上的沙子形成的图样。
二、单摆的回复力
三、单摆的周期
一条短绳系一个小球,它的振动周期较短;
悬绳较长的秋千,周期较长;
单摆的周期与哪些因素有关?
三、单摆的周期
探究单摆周期与摆长之间的关系
在铁架台的横梁上固定两个单摆,按照以下几种情况,把它们拉起一定的小角度后同时释放,观察两摆的振动周期。
1. 摆球质量、摆长相同,振幅不同(都在小偏角下);
周期近似相等。
三、单摆的周期
在铁架台的横梁上固定两个单摆,按照以下几种情况,把它们拉起一定的小角度后同时释放,观察两摆的振动周期。
2. 摆长、振幅相同,摆球质量不同;
周期近似相等。
探究单摆周期与摆长之间的关系
三、单摆的周期
3. 两摆的振幅、摆球质量相同,摆长不同。
周期不相等。
探究单摆周期与摆长之间的关系
三、单摆的周期
在铁架台的横梁上固定两个单摆,按照以下几种情况,把它们拉起一定的小角度后同时释放,观察两摆的振动周期。
综上所述:
实验表明:单摆做简谐运动的周期与摆长有关,摆长越长,周期越大;单摆的周期与摆球质量和振幅无关。
探究单摆周期与摆长之间的关系
三、单摆的周期
为了找出定量的关系,荷兰物理学家惠更斯进行了详尽的研究,发现单摆做简谐运动的周期T与摆长l的二次方根成正比,与重力加速度g的二次方根成反比,而与振幅、摆球质量无关。
惠更斯确定了计算单摆周期的公式(单摆定律):
单摆周期公式的发现,为人类利用简谐运动定量计时提供了可能,并以此为基础发明了真正可持续运转的时钟。
摆钟是一种时钟,由荷兰物理学家惠更斯(Huygens)发明于1656年,根据单摆定律制造,用摆锤控制其它机件,使钟走的快慢均匀,一般能报点,要用发条来提供能量使其摆动。
探究单摆周期与摆长之间的关系
简谐运动与圆的故事
四、有趣的事情…
有趣的是:
绿色小球做匀速周周运动一圈
红色振子做简谐运动一个周期
匀速圆周运动和简谐运动肯定有着密切的联系
有趣的事发生了…
小球和振子任意时刻均在同一竖直线上
简谐运动与圆的故事
质点在x轴上投影的运动是简谐振动
绿球的向心力的水平分力:
则:
红球的回复力:
简谐振动的周期与周圆运动的周期相同
(具有普遍性,对所有的简谐运动都适用)
简谐振动的位移随时间变化:
四、有趣的事情…
w
O
x
A
回到单摆
具有普遍性,
对所有的简谐运动都适用
四、有趣的事情…
l
m
O
G
P
F1
F2
T
规定向右为正方向
结论:单摆在摆角很小的情况下是简谐运动。
单摆:
五、练习与应用
1. 探究单摆周期与摆长之间的一个理想单摆,已知其周期为T。如果由于某种原因(如转移到其他星球)自由落体加速度变为原来的1/2 ,振幅变为原来的1/3,摆长变为原来的1/4,摆球的质量变为原来的1/5,它的周期变为多少?
五、练习与应用
2. 周期是2s的单摆叫秒摆,秒摆的摆长是多少?把一个地球上的秒摆拿到月球上去,已知月球上的自由落体加速度为1.6 m/s2,它在月球上做50次全振动要用多少时间?
五、练习与应用
3. 如图是两个单摆的振动图像。
(1)甲、乙两个摆的摆长之比是多少?
(2)以向右的方向作为摆球偏离平衡位置的位移的正方向,从t=0起,乙第一次到达右方最大位移时,甲摆动到了什么位置?向什么方向运动?
五、练习与应用
4. 一条细线下面挂着一个小球,让它自由摆动,画出它的振动图像如图所示。
(1)请根据图中的数据计算出它的摆长。
(2)请根据图中的数据估算出它摆动的最大偏角。
