数学人教A版2019必修第一册3.2.2函数的性质-奇偶性(共20张ppt)
文档属性
| 名称 | 数学人教A版2019必修第一册3.2.2函数的性质-奇偶性(共20张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-07 12:01:46 | ||
图片预览






文档简介
(共20张PPT)
函数的概念与性质
3.2.2 函数的奇偶性
课程标准
借助具体的函数图像,了解函数的奇偶性的概念和几何意义,理解他们的作用与实际意义
复习回顾
问题1 函数的单调性是如何描述的?
如果,当时,都有,那么就称函数在区间上单调递增.
就叫做函数的单调递增区间,简称增区间.
如果,当时,都有,那么就称函数在区间上单调递减.
就叫做函数的单调递增区间,简称减区间.
一般地,设函数:
复习回顾
问题2 我们如何求函数的最大(小)值?
(2)单调性法:先研究函数的单调性,再利用单调性的意义求函数的最大(小)值.
注:在实际运用中,我们更多的是将这两种方法结合起来,即采用“单调性+图象”的方法。
(1)图象法:先画出函数的图象,再直接函数最值的几何意义利求函数的最大(小)值;
1.图像
2.定义域
3.单调性
4.求最值
接下来,我们继续研究函数的其他性质!
新知导入
剪纸早在我国汉、唐时期就被用来作为装饰品,是中国传统的民间装饰艺术的一种。从题材上分,有人物、动物、景物及花卉、组字等,既有展示历史故事、神话传说的,也有反映现实社会生活、风俗民情的,涉及方方面面。它的历史渊源,它的思想内涵,它的美学价值,更是催人探索、领悟真趣!
从剪纸的图片上,有明显的图像特征:沿中轴线对称,轴对称等。
一些函数的图像也存在类似的特征,我们该如何描述与判断呢?
一
二
三
教学目标
了解函数奇偶性的含义
会判断与证明函数的奇偶性
初步掌握函数性质研究方法,从特殊到一般,从定性到定量,体会数形结合与类比的思想方法。
教学目标
难点
重点
易错点
新知探究
探究一:函数奇偶性的含义
新知讲解
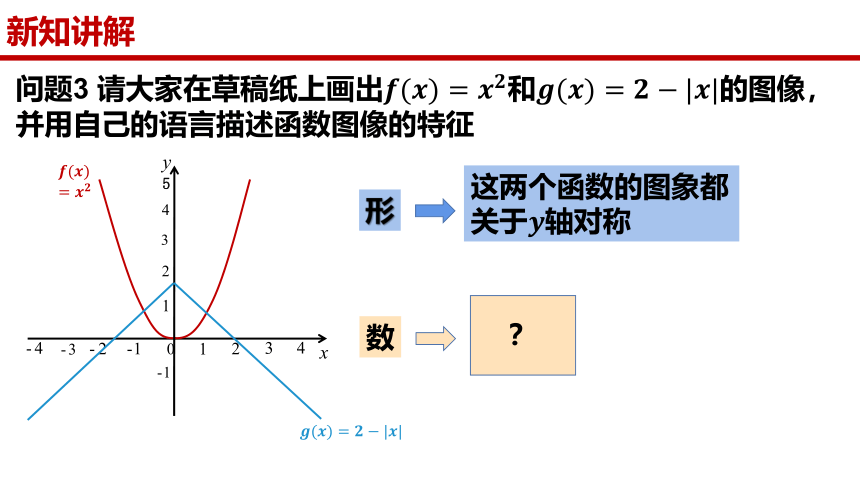
问题3 请大家在草稿纸上画出和的图像,并用自己的语言描述函数图像的特征
5
这两个函数的图象都关于轴对称
形
数
?
概念生成
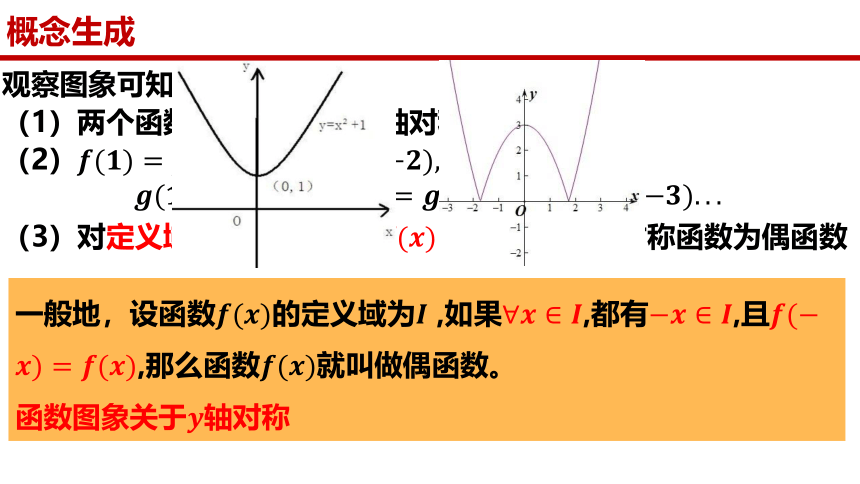
观察图象可知:
(1)两个函数的图象都关于y轴对称。
(2)
(3)对定义域内任意的 ,这时称函数为偶函数
一般地,设函数的定义域为 ,如果,都有,且,那么函数就叫做偶函数。
函数图象关于轴对称
概念生成
一般地,设函数的定义域为 ,如果,都有,且,那么函数就叫做奇函数。
图象关于原点对称
概念小结
一般地,设函数的定义域为 ,如果,都有,且,那么函数就叫做偶函数。函数图象关于轴对称
一般地,设函数的定义域为 ,如果,都有,且,那么函数就叫做奇函数。图象关于原点对称
若函数的定义域为 ,如果,都有,且,那么函数既是奇函数又是偶函数;(如)
若函数的定义域为 ,如果,都有,且,那么函数既不是奇函数也不是偶函数,简称非奇非偶函数.
1.定义域是否关于原点对称
2.根据奇偶性的定义(图像)进行判断
新知探究
探究二:判断、证明函数奇偶性
课堂例题
例6.判断下列函数的奇偶性.
(1)
(2)
(3)
(4)
解:(1)函数的定义域为
∵,都有
且,
∴函数为偶函数.
(2)函数的定义域为
∵,都有
且,
∴函数为奇函数.
1.定义法
2.图像法
例题讲解
解:(3)函数的定义域为
∵,都有,
且,
∴函数为奇函数.
(4)函数的定义域为
∵,都有,
且,
∴函数为偶函数.
求定义域并判断是否关于原点对称
判断的关系
下结论
1.定义域是否关于原点对称
2.根据奇偶性的定义(图像)进行判断
新知探究
探究三:探究根据函数奇偶性求分段函数解析式
合作探究
问题7 以小组的形式讨论下列两个问题。
(1)判断函数的奇偶性.
(2)已知函数图象的一部分,你能根据的奇偶性画出它在轴左边的图象吗?
新知讲解
1.已知函数是上的奇函数,且当在上的解析式.
课本86页第11题
答案:
解:因为,有
当时,
所以
又的奇函数
新知讲解
变式已知函数为上的偶函数,且当时,,则当时,求此时的解析式.
解:当时,,则
∵为上的偶函数
∴当时,.
小结
奇函数
一般地,设函数的定义域为 ,如果,都有,且,那么函数就叫做奇函数。
数
形
图象关于原点对称
偶函数
一般地,设函数的定义域为 ,如果,都有,且,那么函数就叫做奇函数。
数
形
图象关于y轴对称
小结
若函数的定义域为 ,如果,都有,且,那么函数既是奇函数又是偶函数;(如)
若函数的定义域为 ,如果,都有,且,那么函数既不是奇函数也不是偶函数,简称非奇非偶函数.
1.定义域是否关于原点对称
2.根据奇偶性的定义(图像)进行判断
函数的概念与性质
3.2.2 函数的奇偶性
课程标准
借助具体的函数图像,了解函数的奇偶性的概念和几何意义,理解他们的作用与实际意义
复习回顾
问题1 函数的单调性是如何描述的?
如果,当时,都有,那么就称函数在区间上单调递增.
就叫做函数的单调递增区间,简称增区间.
如果,当时,都有,那么就称函数在区间上单调递减.
就叫做函数的单调递增区间,简称减区间.
一般地,设函数:
复习回顾
问题2 我们如何求函数的最大(小)值?
(2)单调性法:先研究函数的单调性,再利用单调性的意义求函数的最大(小)值.
注:在实际运用中,我们更多的是将这两种方法结合起来,即采用“单调性+图象”的方法。
(1)图象法:先画出函数的图象,再直接函数最值的几何意义利求函数的最大(小)值;
1.图像
2.定义域
3.单调性
4.求最值
接下来,我们继续研究函数的其他性质!
新知导入
剪纸早在我国汉、唐时期就被用来作为装饰品,是中国传统的民间装饰艺术的一种。从题材上分,有人物、动物、景物及花卉、组字等,既有展示历史故事、神话传说的,也有反映现实社会生活、风俗民情的,涉及方方面面。它的历史渊源,它的思想内涵,它的美学价值,更是催人探索、领悟真趣!
从剪纸的图片上,有明显的图像特征:沿中轴线对称,轴对称等。
一些函数的图像也存在类似的特征,我们该如何描述与判断呢?
一
二
三
教学目标
了解函数奇偶性的含义
会判断与证明函数的奇偶性
初步掌握函数性质研究方法,从特殊到一般,从定性到定量,体会数形结合与类比的思想方法。
教学目标
难点
重点
易错点
新知探究
探究一:函数奇偶性的含义
新知讲解
问题3 请大家在草稿纸上画出和的图像,并用自己的语言描述函数图像的特征
5
这两个函数的图象都关于轴对称
形
数
?
概念生成
观察图象可知:
(1)两个函数的图象都关于y轴对称。
(2)
(3)对定义域内任意的 ,这时称函数为偶函数
一般地,设函数的定义域为 ,如果,都有,且,那么函数就叫做偶函数。
函数图象关于轴对称
概念生成
一般地,设函数的定义域为 ,如果,都有,且,那么函数就叫做奇函数。
图象关于原点对称
概念小结
一般地,设函数的定义域为 ,如果,都有,且,那么函数就叫做偶函数。函数图象关于轴对称
一般地,设函数的定义域为 ,如果,都有,且,那么函数就叫做奇函数。图象关于原点对称
若函数的定义域为 ,如果,都有,且,那么函数既是奇函数又是偶函数;(如)
若函数的定义域为 ,如果,都有,且,那么函数既不是奇函数也不是偶函数,简称非奇非偶函数.
1.定义域是否关于原点对称
2.根据奇偶性的定义(图像)进行判断
新知探究
探究二:判断、证明函数奇偶性
课堂例题
例6.判断下列函数的奇偶性.
(1)
(2)
(3)
(4)
解:(1)函数的定义域为
∵,都有
且,
∴函数为偶函数.
(2)函数的定义域为
∵,都有
且,
∴函数为奇函数.
1.定义法
2.图像法
例题讲解
解:(3)函数的定义域为
∵,都有,
且,
∴函数为奇函数.
(4)函数的定义域为
∵,都有,
且,
∴函数为偶函数.
求定义域并判断是否关于原点对称
判断的关系
下结论
1.定义域是否关于原点对称
2.根据奇偶性的定义(图像)进行判断
新知探究
探究三:探究根据函数奇偶性求分段函数解析式
合作探究
问题7 以小组的形式讨论下列两个问题。
(1)判断函数的奇偶性.
(2)已知函数图象的一部分,你能根据的奇偶性画出它在轴左边的图象吗?
新知讲解
1.已知函数是上的奇函数,且当在上的解析式.
课本86页第11题
答案:
解:因为,有
当时,
所以
又的奇函数
新知讲解
变式已知函数为上的偶函数,且当时,,则当时,求此时的解析式.
解:当时,,则
∵为上的偶函数
∴当时,.
小结
奇函数
一般地,设函数的定义域为 ,如果,都有,且,那么函数就叫做奇函数。
数
形
图象关于原点对称
偶函数
一般地,设函数的定义域为 ,如果,都有,且,那么函数就叫做奇函数。
数
形
图象关于y轴对称
小结
若函数的定义域为 ,如果,都有,且,那么函数既是奇函数又是偶函数;(如)
若函数的定义域为 ,如果,都有,且,那么函数既不是奇函数也不是偶函数,简称非奇非偶函数.
1.定义域是否关于原点对称
2.根据奇偶性的定义(图像)进行判断
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
