2022--2023学年北师大版数学八年级上册 1.3勾股定理的应用同步精练(Word版含答案)
文档属性
| 名称 | 2022--2023学年北师大版数学八年级上册 1.3勾股定理的应用同步精练(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 293.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-06 00:00:00 | ||
图片预览



文档简介
1.3勾股定理的应用同步精练
一、单选题
1.《九章算术》中有一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去根三尺,问折者高几何?”题意是:如图,一根竹子原高1丈(1丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?若设折断处离地面x尺,则下面所列方程正确的是( )
A. B.
C. D.
2.如图,有一个池塘,其底面是边长为10尺的正方形,一个芦苇AB生长在它的中央,高出水面部分BC为1尺.如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的.则这根芦苇的长度是( )
A.10尺 B.11尺 C.12尺 D.13尺
3.一艘轮船从A港向南偏西方向航行到达B岛,再从B岛沿方向航行到达C岛,A港到航线的最短距离是.若轮船速度为,轮船从C岛沿返回A港所需的时间是( )
A. B. C. D.
4.两只小鼹鼠在地下打洞,一只朝正北方向挖,每分钟挖8cm,另一只朝正东方向挖,每分钟挖6cm,10分钟之后两只小鼹鼠相距( )
A.50cm B.120cm C.140cm D.100cm
5.如图是用硬纸板做成的两个直角边长分别为a,b,斜边长为c的全等三角形拼成的图形,观察图形,可以验证( )
A.a2+b2=c2 B.(a-b)2=a2-2ab+b2 C.a2-b2=(a+b)(a-b) D.(a+b)2=a2+2ab+b2
6.如图,铁路MN和公路PQ在点O处交汇,∠QON=30°.公路PQ上A处距O点240米.如果火车行驶时,周围200米以内会受到噪音的影响.那么火车在铁路MN上沿ON方向以72千米/时的速度行驶时,A处受噪音影响的时间为( )
A.12秒 B.16秒 C.20秒 D.30秒.
7.如图,已知ABCD是长方形纸片,,在CD上存在一点E,沿直线AE将折叠,D恰好落在BC边上的点F处,且,则的面积是( ).
A. B. C. D.
8.如图是一个三级台阶,它的每一级的长、宽、高分别为20dm、3dm、2dm,A和B是这个台阶上两个相对的端点,点A处有一只蚂蚁,想到点B处去吃可口的食物,则蚂蚁沿着台阶面爬行到点B的最短路程为( )
A.20dm B.25dm C.30dm D.35dm
9.如图,三角形纸片ABC,AB=AC,∠BAC=90°,点E为AB中点,沿过点E的直线折叠,使点B与点A重合,折痕现交于点F,已知EF=,则BC的长是( )
A. B.3 C.3 D.3
10.如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )
A.5 B.25 C.10+5 D.35
11.如图,透明的圆柱形玻璃容器(容器厚度忽略不计)的高为12cm,在容器内壁离容器底部4 cm 的点B处有一滴蜂蜜,此时一只蚂蚁正好在容器外壁,且离容器上沿4 cm的点A处,若蚂蚁吃到蜂蜜需爬行的最短路径为15 cm,则该圆柱底面周长为( )cm.
A.9 B.10 C.18 D.20
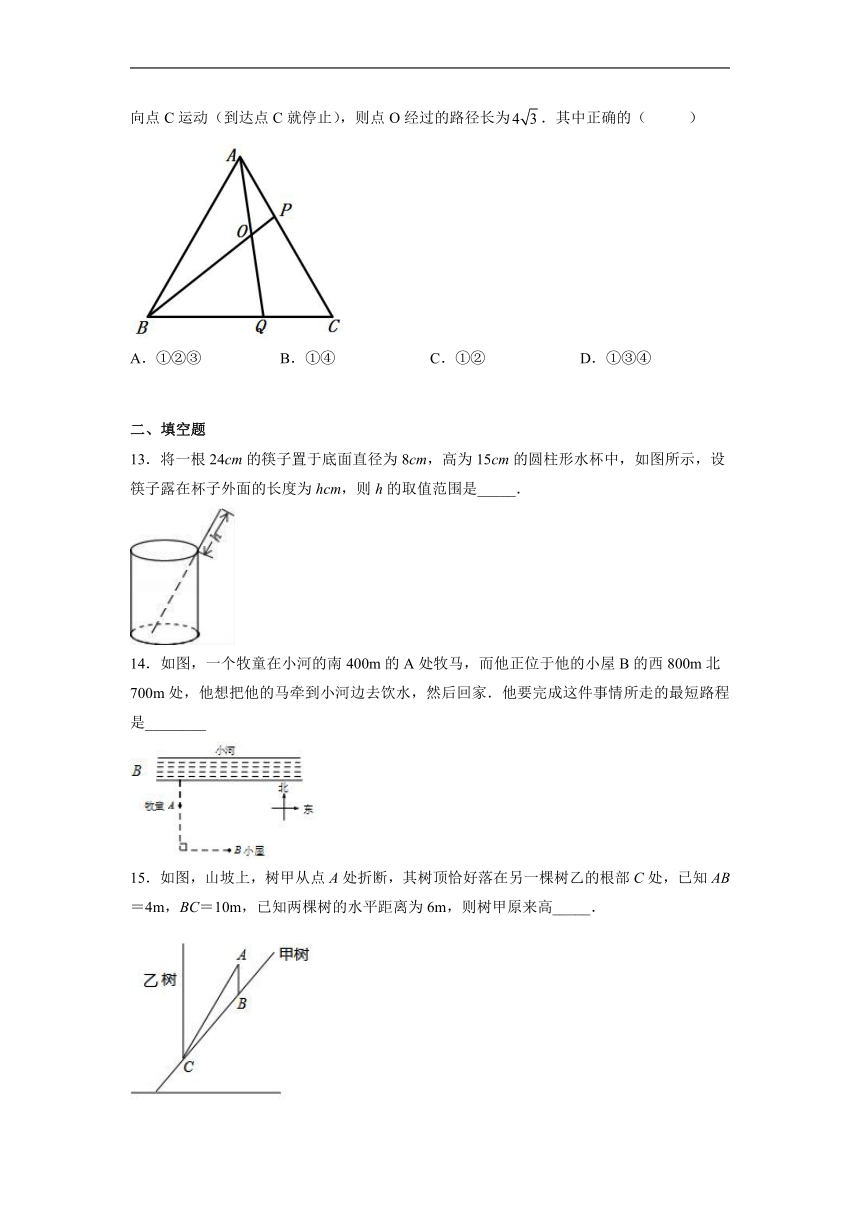
12.如图,等边的边长为8.P,Q分别是边上的点,连结,交于点O.以下结论:①若,则;②若,则;③若,则;④若点P和点Q分别从点A和点B同时出发,以相同的速度向点C运动(到达点C就停止),则点O经过的路径长为.其中正确的( )
A.①②③ B.①④ C.①② D.①③④
二、填空题
13.将一根24cm的筷子置于底面直径为8cm,高为15cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度为hcm,则h的取值范围是_____.
14.如图,一个牧童在小河的南400m的A处牧马,而他正位于他的小屋B的西800m北700m处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是________
15.如图,山坡上,树甲从点A处折断,其树顶恰好落在另一棵树乙的根部C处,已知AB=4m,BC=10m,已知两棵树的水平距离为6m,则树甲原来高_____.
16.如图,滑竿在机械槽内运动,∠ACB为直角,已知滑竿AB长2.5米,顶点A在AC上滑动,量得滑竿下端B距C点的距离为1.5米,当端点B向右移动0.5米时,滑竿顶端A下滑________米.
17.爱动脑筋的小明某天在家玩遥控游戏时遇到下面的问题:已知,如图一个棱长为8cm无盖的正方体铁盒,小明通过遥控器操控一只带有磁性的甲虫玩具,他先把甲虫放在正方体盒子外壁A处,然后遥控甲虫从A处出发沿外壁面正方形ABCD爬行,爬到边CD上后再在边CD上爬行3cm,最后在沿内壁面正方形ABCD上爬行,最终到达内壁BC的中点M,甲虫所走的最短路程是 ______cm
三、解答题
18.如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得BC=100m,AC=60m,求A,B两点间的距离
19.有一只喜鹊在一棵高3米的小树的树梢上觅食,它的巢筑在距离该树24米,高为14米的一棵大树上,且巢离大树顶部为1米,这时,它听到巢中幼鸟求助的叫声,立刻赶过去,如果它的飞行速度为每秒5米,那么它至少几秒能赶回巢中?
20.如图所示,A、B两块试验田相距200m,C为水源地,AC=160m,BC=120m,为了方便灌溉,现有两种方案修筑水渠.
甲方案:从水源地C直接修筑两条水渠分别到A、B;
乙方案;过点C作AB的垂线,垂足为H,先从水源地C修筑一条水渠到AB所在直线上的H处,再从H分别向A、B进行修筑.
(1)请判断△ABC的形状(要求写出推理过程);
(2)两种方案中,哪一种方案所修的水渠较短?请通过计算说明.
21.如图,公路MN和公路PQ在点P处交会,公路PQ上点A处有学校,点A到公路MN的距离为80m,现有一拖拉机在公路MN上以18km/h的速度沿PN方向行驶,拖拉机行驶时周围100m以内都会受到噪音的影响,试问该校受影响的时间为多长?
参考答案
1--10DDDDA BBBBB 11--12CB
12.B
13.7cm≤h≤9cm.
14.1700m
15.(4+6)m
16.0.5
17.16
18.解:在Rt△ABC中,,BC=100m,AC=60m,由勾股定理得:
,
即A、B两点间的距离为80m.
19.解:如图所示,米,米,米,米.
过点作于点.
在中,米,
米,
所以.
所以喜鹊离巢的距离米.
喜鹊赶回巢所需的时间为(秒).即它至少5.2秒能赶回巢中.
20.解:(1)△ABC是直角三角形;
理由如下:
∴AC2+BC2=1602+1202=40000,AB2=2002=40000,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,∠ACB=90°;
(2)甲方案所修的水渠较短;
理由如下:
∵△ABC是直角三角形,
∴△ABC的面积=AB CH=AC BC,
∴CH=(m),
∵AC+BC=160+120=280(m),CH+AH+BH=CH+AB=96+200=296(m),
∴AC+BC<CH+AH+BH,
∴甲方案所修的水渠较短.
21.设拖拉机开到C处刚好开始受到影响,行驶到D处时结束了噪声的影响.
则有CA=DA=100m,
在Rt△ABC中,CB==60(m),
∴CD=2CB=120m,
∵18km/h=18000m/3600s=5m/s,
∴该校受影响的时间为:120÷5=24(s).
答:该校受影响拖拉机产生的噪声的影响时间为24秒.
一、单选题
1.《九章算术》中有一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去根三尺,问折者高几何?”题意是:如图,一根竹子原高1丈(1丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?若设折断处离地面x尺,则下面所列方程正确的是( )
A. B.
C. D.
2.如图,有一个池塘,其底面是边长为10尺的正方形,一个芦苇AB生长在它的中央,高出水面部分BC为1尺.如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的.则这根芦苇的长度是( )
A.10尺 B.11尺 C.12尺 D.13尺
3.一艘轮船从A港向南偏西方向航行到达B岛,再从B岛沿方向航行到达C岛,A港到航线的最短距离是.若轮船速度为,轮船从C岛沿返回A港所需的时间是( )
A. B. C. D.
4.两只小鼹鼠在地下打洞,一只朝正北方向挖,每分钟挖8cm,另一只朝正东方向挖,每分钟挖6cm,10分钟之后两只小鼹鼠相距( )
A.50cm B.120cm C.140cm D.100cm
5.如图是用硬纸板做成的两个直角边长分别为a,b,斜边长为c的全等三角形拼成的图形,观察图形,可以验证( )
A.a2+b2=c2 B.(a-b)2=a2-2ab+b2 C.a2-b2=(a+b)(a-b) D.(a+b)2=a2+2ab+b2
6.如图,铁路MN和公路PQ在点O处交汇,∠QON=30°.公路PQ上A处距O点240米.如果火车行驶时,周围200米以内会受到噪音的影响.那么火车在铁路MN上沿ON方向以72千米/时的速度行驶时,A处受噪音影响的时间为( )
A.12秒 B.16秒 C.20秒 D.30秒.
7.如图,已知ABCD是长方形纸片,,在CD上存在一点E,沿直线AE将折叠,D恰好落在BC边上的点F处,且,则的面积是( ).
A. B. C. D.
8.如图是一个三级台阶,它的每一级的长、宽、高分别为20dm、3dm、2dm,A和B是这个台阶上两个相对的端点,点A处有一只蚂蚁,想到点B处去吃可口的食物,则蚂蚁沿着台阶面爬行到点B的最短路程为( )
A.20dm B.25dm C.30dm D.35dm
9.如图,三角形纸片ABC,AB=AC,∠BAC=90°,点E为AB中点,沿过点E的直线折叠,使点B与点A重合,折痕现交于点F,已知EF=,则BC的长是( )
A. B.3 C.3 D.3
10.如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )
A.5 B.25 C.10+5 D.35
11.如图,透明的圆柱形玻璃容器(容器厚度忽略不计)的高为12cm,在容器内壁离容器底部4 cm 的点B处有一滴蜂蜜,此时一只蚂蚁正好在容器外壁,且离容器上沿4 cm的点A处,若蚂蚁吃到蜂蜜需爬行的最短路径为15 cm,则该圆柱底面周长为( )cm.
A.9 B.10 C.18 D.20
12.如图,等边的边长为8.P,Q分别是边上的点,连结,交于点O.以下结论:①若,则;②若,则;③若,则;④若点P和点Q分别从点A和点B同时出发,以相同的速度向点C运动(到达点C就停止),则点O经过的路径长为.其中正确的( )
A.①②③ B.①④ C.①② D.①③④
二、填空题
13.将一根24cm的筷子置于底面直径为8cm,高为15cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度为hcm,则h的取值范围是_____.
14.如图,一个牧童在小河的南400m的A处牧马,而他正位于他的小屋B的西800m北700m处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是________
15.如图,山坡上,树甲从点A处折断,其树顶恰好落在另一棵树乙的根部C处,已知AB=4m,BC=10m,已知两棵树的水平距离为6m,则树甲原来高_____.
16.如图,滑竿在机械槽内运动,∠ACB为直角,已知滑竿AB长2.5米,顶点A在AC上滑动,量得滑竿下端B距C点的距离为1.5米,当端点B向右移动0.5米时,滑竿顶端A下滑________米.
17.爱动脑筋的小明某天在家玩遥控游戏时遇到下面的问题:已知,如图一个棱长为8cm无盖的正方体铁盒,小明通过遥控器操控一只带有磁性的甲虫玩具,他先把甲虫放在正方体盒子外壁A处,然后遥控甲虫从A处出发沿外壁面正方形ABCD爬行,爬到边CD上后再在边CD上爬行3cm,最后在沿内壁面正方形ABCD上爬行,最终到达内壁BC的中点M,甲虫所走的最短路程是 ______cm
三、解答题
18.如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得BC=100m,AC=60m,求A,B两点间的距离
19.有一只喜鹊在一棵高3米的小树的树梢上觅食,它的巢筑在距离该树24米,高为14米的一棵大树上,且巢离大树顶部为1米,这时,它听到巢中幼鸟求助的叫声,立刻赶过去,如果它的飞行速度为每秒5米,那么它至少几秒能赶回巢中?
20.如图所示,A、B两块试验田相距200m,C为水源地,AC=160m,BC=120m,为了方便灌溉,现有两种方案修筑水渠.
甲方案:从水源地C直接修筑两条水渠分别到A、B;
乙方案;过点C作AB的垂线,垂足为H,先从水源地C修筑一条水渠到AB所在直线上的H处,再从H分别向A、B进行修筑.
(1)请判断△ABC的形状(要求写出推理过程);
(2)两种方案中,哪一种方案所修的水渠较短?请通过计算说明.
21.如图,公路MN和公路PQ在点P处交会,公路PQ上点A处有学校,点A到公路MN的距离为80m,现有一拖拉机在公路MN上以18km/h的速度沿PN方向行驶,拖拉机行驶时周围100m以内都会受到噪音的影响,试问该校受影响的时间为多长?
参考答案
1--10DDDDA BBBBB 11--12CB
12.B
13.7cm≤h≤9cm.
14.1700m
15.(4+6)m
16.0.5
17.16
18.解:在Rt△ABC中,,BC=100m,AC=60m,由勾股定理得:
,
即A、B两点间的距离为80m.
19.解:如图所示,米,米,米,米.
过点作于点.
在中,米,
米,
所以.
所以喜鹊离巢的距离米.
喜鹊赶回巢所需的时间为(秒).即它至少5.2秒能赶回巢中.
20.解:(1)△ABC是直角三角形;
理由如下:
∴AC2+BC2=1602+1202=40000,AB2=2002=40000,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,∠ACB=90°;
(2)甲方案所修的水渠较短;
理由如下:
∵△ABC是直角三角形,
∴△ABC的面积=AB CH=AC BC,
∴CH=(m),
∵AC+BC=160+120=280(m),CH+AH+BH=CH+AB=96+200=296(m),
∴AC+BC<CH+AH+BH,
∴甲方案所修的水渠较短.
21.设拖拉机开到C处刚好开始受到影响,行驶到D处时结束了噪声的影响.
则有CA=DA=100m,
在Rt△ABC中,CB==60(m),
∴CD=2CB=120m,
∵18km/h=18000m/3600s=5m/s,
∴该校受影响的时间为:120÷5=24(s).
答:该校受影响拖拉机产生的噪声的影响时间为24秒.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
