13.2.4三角形的外角 课件(共31张PPT)
文档属性
| 名称 | 13.2.4三角形的外角 课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 347.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-06 00:00:00 | ||
图片预览

文档简介
(共31张PPT)
13.2.4 三角形的外角
1、在△ABC中,∠A=80°, ∠B=52°,则∠C= .
3、什么是三角形的内角?其内角和等于多少?
48 °
三角形中,相邻两边所夹的角叫作三角形的内角.
三角形的内角和是 180°
2、如图,在△ABC中, ∠A=70°, ∠B=60°,
则∠ACB= ,∠ACD= .
A
B
C
D
50°
130°
课前热身
转化为一个平角或同旁内角互补等,
思路总结
C
B
A
E
D
2
1
C
B
A
D
E
C
B
A
D
A
B
C
D
F
E
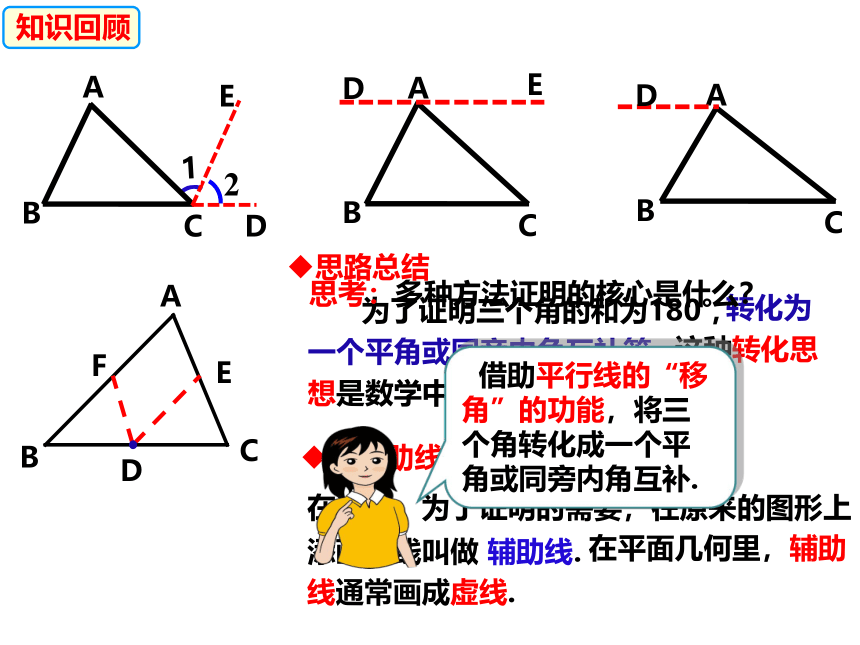
这种转化思想是数学中的常用方法.
为了证明三个角的和为180°,
作辅助线
在这里,为了证明的需要,在原来的图形上添画的线叫做 辅助线.
在平面几何里,辅助线通常画成虚线.
思考:多种方法证明的核心是什么?
借助平行线的“移角”的功能,将三个角转化成一个平角或同旁内角互补.
知识回顾
把 △ABC 的一边 BC 延长至点 D,
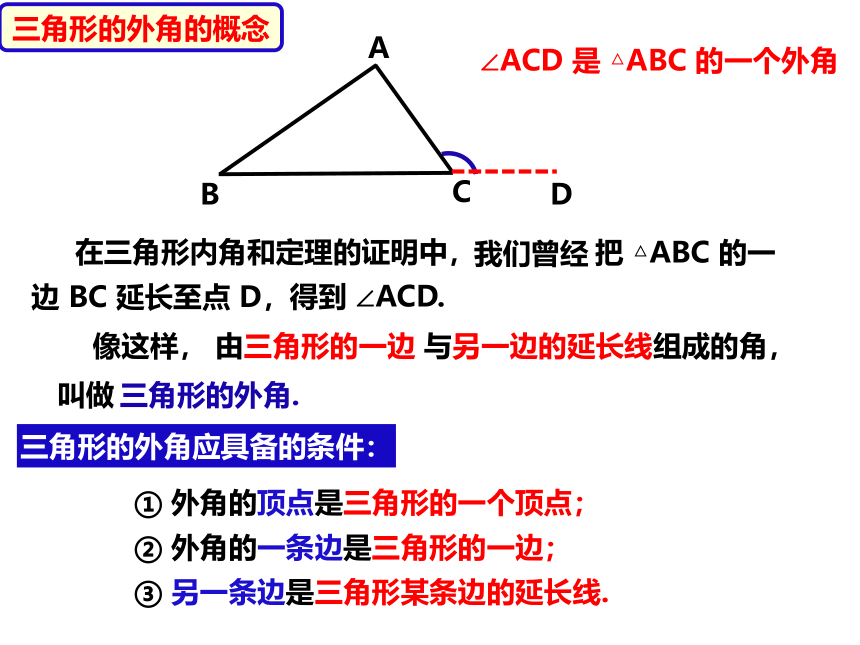
三角形的外角的概念
叫做
在三角形内角和定理的证明中,
得到 ∠ACD.
我们曾经
像这样,
由三角形的一边
与另一边的延长线组成的角,
三角形的外角.
C
B
A
D
∠ACD 是 △ABC 的一个外角
三角形的外角应具备的条件:
① 外角的顶点是三角形的一个顶点;
② 外角的一条边是三角形的一边;
③ 另一条边是三角形某条边的延长线.
在三角形的每个顶点处有多少个外角?
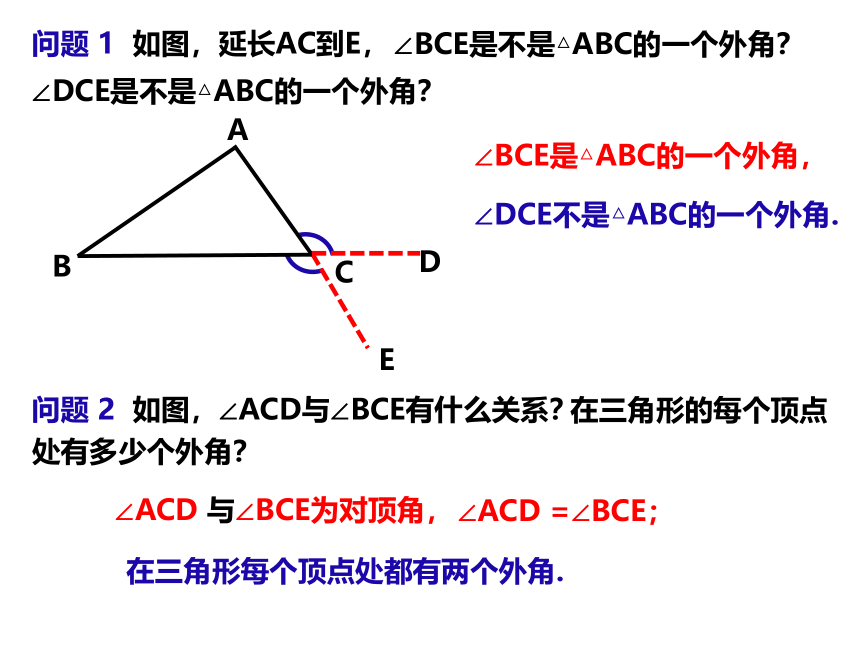
问题 1 如图,延长AC到E,
∠DCE是不是△ABC的一个外角?
E
C
B
A
D
∠BCE是不是△ABC的一个外角?
∠BCE是△ABC的一个外角,
∠DCE不是△ABC的一个外角.
问题 2 如图,∠ACD与∠BCE有什么关系?
在三角形每个顶点处都有两个外角.
∠ACD 与∠BCE为对顶角,
∠ACD =∠BCE;
A
B
C
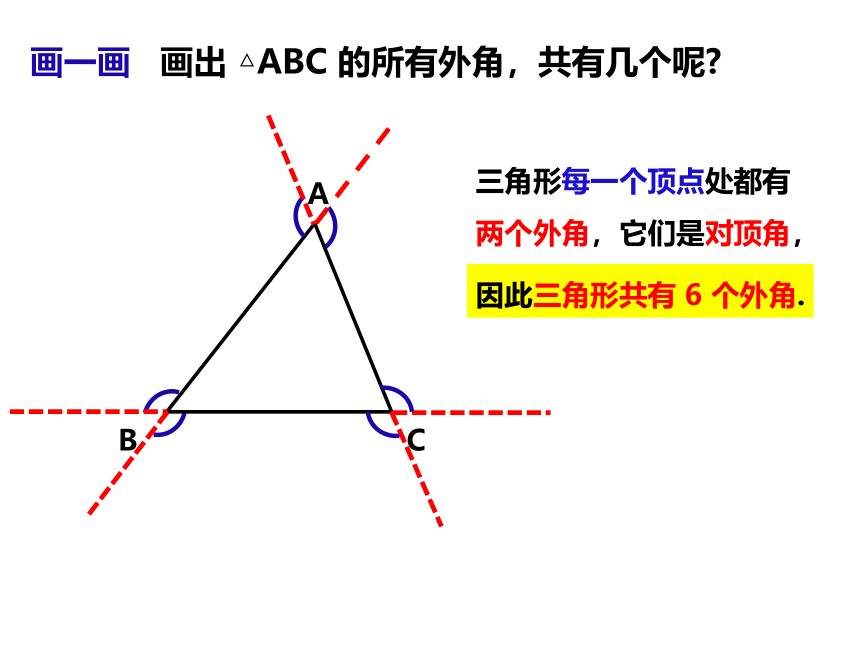
画一画 画出 △ABC 的所有外角,共有几个呢
三角形每一个顶点处都有两个外角,它们是对顶角,
因此三角形共有 6 个外角.
F
A
B
C
D
E
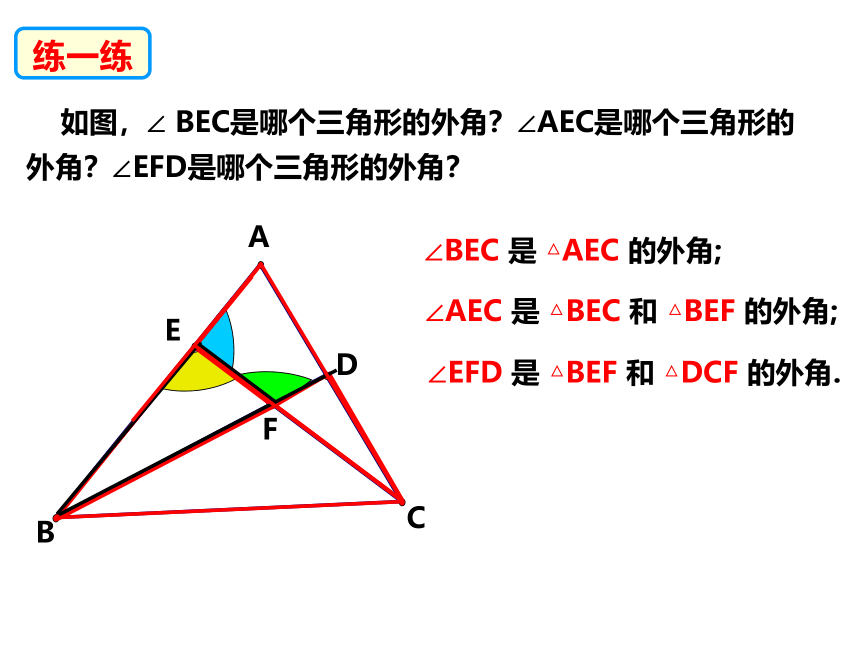
如图,∠ BEC是哪个三角形的外角?∠AEC是哪个三角形的外角?∠EFD是哪个三角形的外角?
∠BEC 是 △AEC 的外角;
∠AEC 是 △BEC 和 △BEF 的外角;
∠EFD 是 △BEF 和 △DCF 的外角.
练一练
三角形的外角的性质
三角形的外角
A
C
B
D
相邻的内角
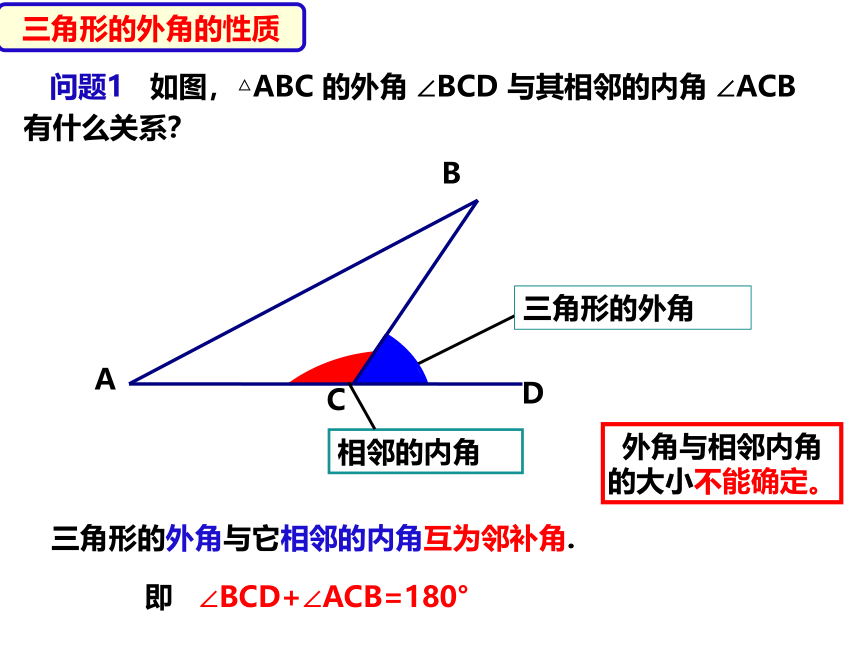
问题1 如图,△ABC 的外角 ∠BCD 与其相邻的内角 ∠ACB 有什么关系?
即 ∠BCD+∠ACB=180°
三角形的外角与它相邻的内角互为邻补角.
外角与相邻内角的大小不能确定。
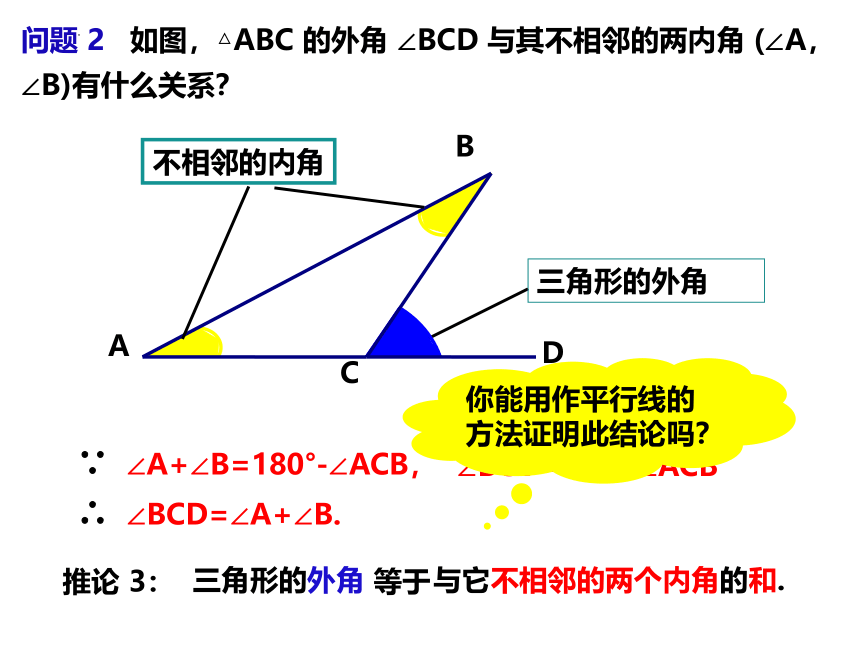
问题 2 如图,△ABC 的外角 ∠BCD 与其不相邻的两内角 (∠A,∠B)有什么关系?
三角形的外角
A
C
B
D
不相邻的内角
∴ ∠BCD=∠A+∠B.
∵ ∠A+∠B=180°-∠ACB,
∠BCD=180°-∠ACB
你能用作平行线的方法证明此结论吗?
三角形的外角
与它不相邻的两个内角的和.
等于
推论 3:
D
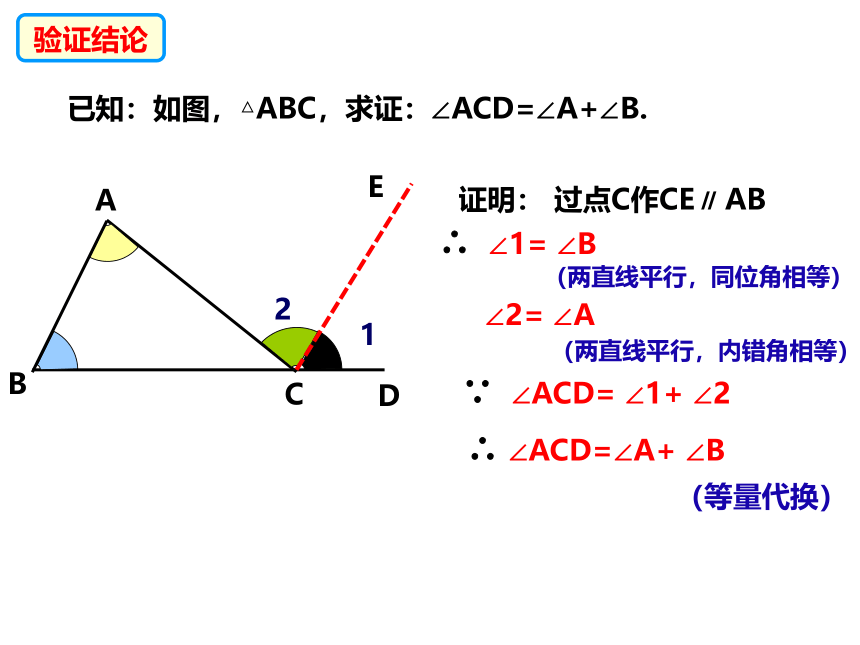
过点C作CE∥ AB
A
B
C
1
2
∴ ∠1= ∠B
∠2= ∠A
∵ ∠ACD= ∠1+ ∠2
E
已知:如图,△ABC,求证:∠ACD=∠A+∠B.
验证结论
∴ ∠ACD=∠A+ ∠B
(两直线平行,内错角相等)
(两直线平行,同位角相等)
证明:
(等量代换)
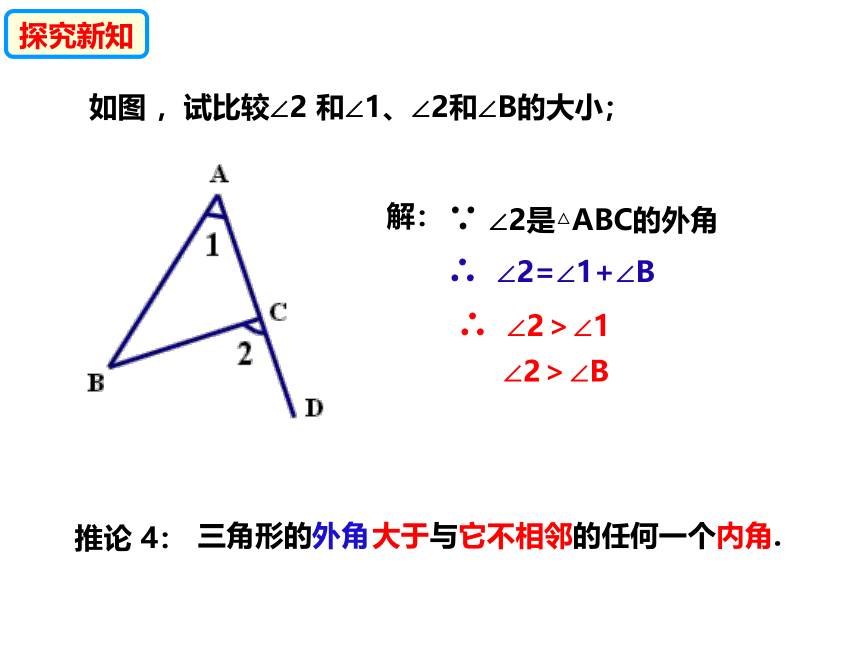
如图 ,试比较∠2 和∠1、∠2和∠B的大小;
∴ ∠2>∠1
探究新知
解:
∴ ∠2=∠1+∠B
∠2>∠B
推论 4:
大于与它不相邻的任何一个内角.
三角形的外角
∵ ∠2是△ABC的外角
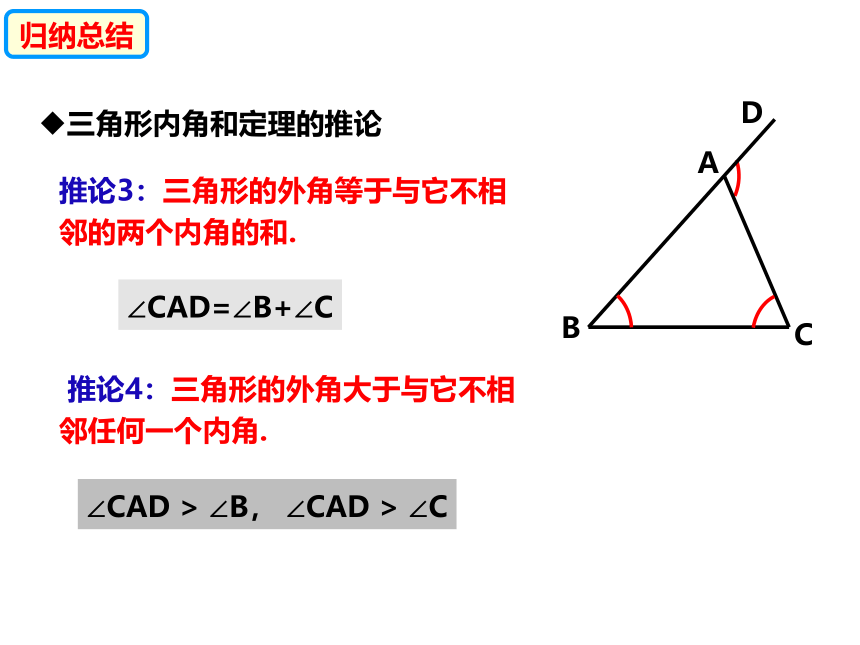
推论3:三角形的外角等于与它不相邻的两个内角的和.
推论4:三角形的外角大于与它不相邻任何一个内角.
A
B
C
D
∠CAD=∠B+∠C
∠CAD > ∠B, ∠CAD > ∠C
三角形内角和定理的推论
归纳总结
1
60°
110°
1、求下列各图中 ∠1 和 ∠2 的度数.
35°
120°
1
A
B
C
2
1
130°
32°
∠1=18 °, ∠2=50 °
(1)
(2)
(3)
∠1=85°
∠1=130°
对于一个外角及与它不相邻的两个内角,若已知其中任意两个角的度数,则可以求出第三个角度数.
知识拓展:
2、如图、∠A=42°,∠ABD=28°,∠ACE=18°,求∠BFC的度数.
F
A
C
D
E
B
对应练习
∵ ∠A=42° ,∠ACE=18°
∴ ∠BEC= ∠A+ ∠ACE=60°
∵ ∠ABD=28° ,∠BEC=60°
∴ ∠BFC= ∠ABD+ ∠BEF =88°
解:
(三角形的外角等于与它不相邻的两个内角的和)
(三角形的外角等于与它不相邻的两个内角的和)
3、如图,∠A=60°,∠B=20°,∠C=30°,求∠BDC的度数.
A
B
C
D
解法一:
延长BD 交 AC 于点 E.
E
∵ ∠A=60°,∠B=20°
∴ ∠DEC
=80°
=∠A+∠B
∵ ∠DEC=80°,∠C=30°
∴ ∠BDC
=110°
=∠DEC+∠C
解法二:
延长CD交AB于点F(解题过程同解法一).
巩固练习
思路点拨:添加适当的辅助线将四边形问题转化为三角形问题.
3、如图,∠A=60°,∠B=20°,∠C=30°,求 ∠BDC 的度数.
A
B
C
D
解法三:
连接AD,并延长到点E.
E
1
2
3
4
∠4=∠2+∠C
∴ ∠3=∠1+∠B,
∴ ∠BDC=∠3+∠4
=∠1+∠B+∠2+∠C
=∠BAC+∠B+∠C
又∵ ∠A=60°,∠B=20°,∠C=30°
∴ ∠BDC=
=110°
60°+20°+30°
(三角形的外角等于与它不相邻的两个内角的和)
巩固练习
(等量代换)
解题的关键是正确的构造三角形,利用三角形外角的性质及转化的思想,把未知角与已知角联系起来求解.
总结
4、如图,P 为 △ABC 内一点,∠BPC=150°,∠ABP=20°,∠ACP=30°,求 ∠A 的度数.
E
对应练习
E
解析:延长 BP 交 AC 于 E 或连接 AP 并延长,构造三角形的外角,再利用外角的性质即可求出 ∠A 的度数.
对应练习
5、如图 ,试比较 ∠3 、∠2、 ∠1 的大小 .
∴ ∠3>∠2
解:
∵ ∠2 是 △ABC 的外角
∴ ∠2>∠1
又 ∵ ∠3 是 △DCE 的外角
∴ ∠3>∠2>∠1
(三角形的外角大于与它不相邻任何一个内角)
(三角形的外角大于与它不相邻任何一个内角)
6、已知:如图,D 是 △ABC内的一点.
求证:∠BDC>∠A
对应练习
A
B
C
D
E
例 5 如图, ∠1, ∠2, ∠3是△ABC的三个外角.
求证:∠1+∠2+∠3=360°
A
B
C
1
2
3
证明:
∵ ∠1=∠ABC+∠ACB
∠2=∠BAC+∠BCA
∠3=∠BAC+∠ABC
(三角形的外角等于与它不相邻的两个内角的和)
∠ABC+∠ACB+∠BAC+∠BCA+∠BAC+∠ABC
∴ ∠1+∠2+∠3=360°
=2(∠ABC+∠ACB+∠BAC)
∵ ∠ABC+∠ACB+∠BAC=180°
∴ ∠1+∠2+∠3=
你还有其他解法吗?
(三角形内角和定理)
(等式的性质)
(等量代换)
例 5 如图, ∠1, ∠2, ∠3是△ABC的三个外角.
求证:∠1+∠2+∠3=360°
A
B
C
1
2
3
证明:
∵ ∠1+∠BAC=180°
∠2+∠ABC=180°
∠3+∠BCA=180°
(平角的定义)
∴ ∠1+∠2+∠3=360°
∵ ∠BAC+∠ABC+∠BCA=180°
∴ ∠1+∠2+∠3+∠BAC+∠ABC+∠BCA=540°
方法二:
(等式的性质)
(三角形内角和定理)
(等式的性质)
例 5 如图, ∠1, ∠2, ∠3是△ABC的三个外角.
求证:∠1+∠2+∠3=360°
A
B
C
1
2
3
证明:
过点A作AD∥ BC
∴ ∠2=∠4
∠3=∠DAC
(两直线平行,同位角相等)
∴ ∠1+∠2+∠3=360°
∵ ∠1+∠4+∠DAC=360°
方法三:
(周角的定义)
(等量代换)
D
4
思考 你能总结出三角形三个外角 (三个顶点处各取一个) 和的数量关系吗?
三角形的三个外角(三个顶点处各取一个) 的和等于360°.
即: 三角形的外角和等于360°.
A
B
C
D
E
1、如图,求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数.
解法一:
连接 CD
F
∵ ∠B+∠E=180°-∠BFE
∠ECD+∠BDC=180°-∠CFD
又∵ ∠BFE=∠CFD
∴ ∠B+∠E=∠ECD+∠BDC
∵∠A+∠ACE+∠ECD+∠BDC+∠ADB=180°
∴ ∠A+∠ACE+∠B+∠E+∠ADB=180°
G
巩固练习
把分散的角集中到同一个三角形中,最后利用三角形的内角和定理去解决问题.
即利用“8”字型图形的性质
总结
A
B
C
D
E
1、如图,求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数.
F
G
解法二:
∵ ∠BFC=∠B+∠E
∠CGD=∠A+∠D
又∵ ∠C+∠BFC+∠CGD=180°
∴ ∠C+∠B+∠E+∠A+∠D=180°
即 ∠A+ ∠B+ ∠C+ ∠D+ ∠E=180°
本题的两种解法都体现了化分散为集中的转化思想,
或 运用外角的性质,
巩固练习
A
B
C
D
E
F
2、如图,求 ∠A+ ∠B+ ∠C+ ∠D+ ∠E 的度数.
解法一:
连接 CB
∵ ∠E+∠F+∠EDF=180°
∠DBC+∠DCB+∠BDC=180°
又∵ ∠EDF=∠BDC
∴ ∠E+∠F=∠DBC+∠DCB
∵∠A+∠ABF+∠FBC+∠DCB+∠ACD=180°
∴ ∠A+∠ABE+∠E+∠F+∠ACB=180°
巩固练习
2、如图,求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数.
解法二:
∵ ∠BGC=∠A+∠C
∠BDG=∠DEF+∠F
又∵ ∠B+∠BGC+∠BDG=180°
∴ ∠B+∠A+∠C+∠DEF+∠F=180°
A
B
C
D
E
F
延长CD交AB于点G.
G
巩固练习
E
3、如图,试求出∠A+∠B+∠C+∠D+∠E+∠F=________.
360°
B
A
C
P
N
M
D
F
三角形的外角和等于360°.
对应练习
4、如图所示,点D,E,F分别是 △ABC 的边 BC,AC,AB 上的点,则 ∠1,∠2,∠3,∠4,∠5,∠6 这六个角的度数的和是 .
对应练习
5、如图,△ABC中,∠A=40°,
(1) 若点 P 是 ∠ABC 与 ∠ACB 平分线的交点,求 ∠P 的度数;
(2) 若点 P 是 ∠CBD 与 ∠BCE 平分线的交点,求 ∠P 的度数;
(3) 若点 P 是 ∠ABC 与 ∠ACF 平分线的交点,求 ∠P 的度数;
∠P=90°+ ∠A
1
2
∠P=90°- ∠A
1
2
∠P= ∠A
1
2
巩固练习
本节课你有什么收获?
三角形的外角
定义
由三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
性质
推论3:三角形的外角等于与它不相邻的两个内角的和
三角形的外角和
三角形的外角和等于360°
推论4:三角形的外角大于与它不相邻的任何一个内角
(三个顶点处各取一个)
13.2.4 三角形的外角
1、在△ABC中,∠A=80°, ∠B=52°,则∠C= .
3、什么是三角形的内角?其内角和等于多少?
48 °
三角形中,相邻两边所夹的角叫作三角形的内角.
三角形的内角和是 180°
2、如图,在△ABC中, ∠A=70°, ∠B=60°,
则∠ACB= ,∠ACD= .
A
B
C
D
50°
130°
课前热身
转化为一个平角或同旁内角互补等,
思路总结
C
B
A
E
D
2
1
C
B
A
D
E
C
B
A
D
A
B
C
D
F
E
这种转化思想是数学中的常用方法.
为了证明三个角的和为180°,
作辅助线
在这里,为了证明的需要,在原来的图形上添画的线叫做 辅助线.
在平面几何里,辅助线通常画成虚线.
思考:多种方法证明的核心是什么?
借助平行线的“移角”的功能,将三个角转化成一个平角或同旁内角互补.
知识回顾
把 △ABC 的一边 BC 延长至点 D,
三角形的外角的概念
叫做
在三角形内角和定理的证明中,
得到 ∠ACD.
我们曾经
像这样,
由三角形的一边
与另一边的延长线组成的角,
三角形的外角.
C
B
A
D
∠ACD 是 △ABC 的一个外角
三角形的外角应具备的条件:
① 外角的顶点是三角形的一个顶点;
② 外角的一条边是三角形的一边;
③ 另一条边是三角形某条边的延长线.
在三角形的每个顶点处有多少个外角?
问题 1 如图,延长AC到E,
∠DCE是不是△ABC的一个外角?
E
C
B
A
D
∠BCE是不是△ABC的一个外角?
∠BCE是△ABC的一个外角,
∠DCE不是△ABC的一个外角.
问题 2 如图,∠ACD与∠BCE有什么关系?
在三角形每个顶点处都有两个外角.
∠ACD 与∠BCE为对顶角,
∠ACD =∠BCE;
A
B
C
画一画 画出 △ABC 的所有外角,共有几个呢
三角形每一个顶点处都有两个外角,它们是对顶角,
因此三角形共有 6 个外角.
F
A
B
C
D
E
如图,∠ BEC是哪个三角形的外角?∠AEC是哪个三角形的外角?∠EFD是哪个三角形的外角?
∠BEC 是 △AEC 的外角;
∠AEC 是 △BEC 和 △BEF 的外角;
∠EFD 是 △BEF 和 △DCF 的外角.
练一练
三角形的外角的性质
三角形的外角
A
C
B
D
相邻的内角
问题1 如图,△ABC 的外角 ∠BCD 与其相邻的内角 ∠ACB 有什么关系?
即 ∠BCD+∠ACB=180°
三角形的外角与它相邻的内角互为邻补角.
外角与相邻内角的大小不能确定。
问题 2 如图,△ABC 的外角 ∠BCD 与其不相邻的两内角 (∠A,∠B)有什么关系?
三角形的外角
A
C
B
D
不相邻的内角
∴ ∠BCD=∠A+∠B.
∵ ∠A+∠B=180°-∠ACB,
∠BCD=180°-∠ACB
你能用作平行线的方法证明此结论吗?
三角形的外角
与它不相邻的两个内角的和.
等于
推论 3:
D
过点C作CE∥ AB
A
B
C
1
2
∴ ∠1= ∠B
∠2= ∠A
∵ ∠ACD= ∠1+ ∠2
E
已知:如图,△ABC,求证:∠ACD=∠A+∠B.
验证结论
∴ ∠ACD=∠A+ ∠B
(两直线平行,内错角相等)
(两直线平行,同位角相等)
证明:
(等量代换)
如图 ,试比较∠2 和∠1、∠2和∠B的大小;
∴ ∠2>∠1
探究新知
解:
∴ ∠2=∠1+∠B
∠2>∠B
推论 4:
大于与它不相邻的任何一个内角.
三角形的外角
∵ ∠2是△ABC的外角
推论3:三角形的外角等于与它不相邻的两个内角的和.
推论4:三角形的外角大于与它不相邻任何一个内角.
A
B
C
D
∠CAD=∠B+∠C
∠CAD > ∠B, ∠CAD > ∠C
三角形内角和定理的推论
归纳总结
1
60°
110°
1、求下列各图中 ∠1 和 ∠2 的度数.
35°
120°
1
A
B
C
2
1
130°
32°
∠1=18 °, ∠2=50 °
(1)
(2)
(3)
∠1=85°
∠1=130°
对于一个外角及与它不相邻的两个内角,若已知其中任意两个角的度数,则可以求出第三个角度数.
知识拓展:
2、如图、∠A=42°,∠ABD=28°,∠ACE=18°,求∠BFC的度数.
F
A
C
D
E
B
对应练习
∵ ∠A=42° ,∠ACE=18°
∴ ∠BEC= ∠A+ ∠ACE=60°
∵ ∠ABD=28° ,∠BEC=60°
∴ ∠BFC= ∠ABD+ ∠BEF =88°
解:
(三角形的外角等于与它不相邻的两个内角的和)
(三角形的外角等于与它不相邻的两个内角的和)
3、如图,∠A=60°,∠B=20°,∠C=30°,求∠BDC的度数.
A
B
C
D
解法一:
延长BD 交 AC 于点 E.
E
∵ ∠A=60°,∠B=20°
∴ ∠DEC
=80°
=∠A+∠B
∵ ∠DEC=80°,∠C=30°
∴ ∠BDC
=110°
=∠DEC+∠C
解法二:
延长CD交AB于点F(解题过程同解法一).
巩固练习
思路点拨:添加适当的辅助线将四边形问题转化为三角形问题.
3、如图,∠A=60°,∠B=20°,∠C=30°,求 ∠BDC 的度数.
A
B
C
D
解法三:
连接AD,并延长到点E.
E
1
2
3
4
∠4=∠2+∠C
∴ ∠3=∠1+∠B,
∴ ∠BDC=∠3+∠4
=∠1+∠B+∠2+∠C
=∠BAC+∠B+∠C
又∵ ∠A=60°,∠B=20°,∠C=30°
∴ ∠BDC=
=110°
60°+20°+30°
(三角形的外角等于与它不相邻的两个内角的和)
巩固练习
(等量代换)
解题的关键是正确的构造三角形,利用三角形外角的性质及转化的思想,把未知角与已知角联系起来求解.
总结
4、如图,P 为 △ABC 内一点,∠BPC=150°,∠ABP=20°,∠ACP=30°,求 ∠A 的度数.
E
对应练习
E
解析:延长 BP 交 AC 于 E 或连接 AP 并延长,构造三角形的外角,再利用外角的性质即可求出 ∠A 的度数.
对应练习
5、如图 ,试比较 ∠3 、∠2、 ∠1 的大小 .
∴ ∠3>∠2
解:
∵ ∠2 是 △ABC 的外角
∴ ∠2>∠1
又 ∵ ∠3 是 △DCE 的外角
∴ ∠3>∠2>∠1
(三角形的外角大于与它不相邻任何一个内角)
(三角形的外角大于与它不相邻任何一个内角)
6、已知:如图,D 是 △ABC内的一点.
求证:∠BDC>∠A
对应练习
A
B
C
D
E
例 5 如图, ∠1, ∠2, ∠3是△ABC的三个外角.
求证:∠1+∠2+∠3=360°
A
B
C
1
2
3
证明:
∵ ∠1=∠ABC+∠ACB
∠2=∠BAC+∠BCA
∠3=∠BAC+∠ABC
(三角形的外角等于与它不相邻的两个内角的和)
∠ABC+∠ACB+∠BAC+∠BCA+∠BAC+∠ABC
∴ ∠1+∠2+∠3=360°
=2(∠ABC+∠ACB+∠BAC)
∵ ∠ABC+∠ACB+∠BAC=180°
∴ ∠1+∠2+∠3=
你还有其他解法吗?
(三角形内角和定理)
(等式的性质)
(等量代换)
例 5 如图, ∠1, ∠2, ∠3是△ABC的三个外角.
求证:∠1+∠2+∠3=360°
A
B
C
1
2
3
证明:
∵ ∠1+∠BAC=180°
∠2+∠ABC=180°
∠3+∠BCA=180°
(平角的定义)
∴ ∠1+∠2+∠3=360°
∵ ∠BAC+∠ABC+∠BCA=180°
∴ ∠1+∠2+∠3+∠BAC+∠ABC+∠BCA=540°
方法二:
(等式的性质)
(三角形内角和定理)
(等式的性质)
例 5 如图, ∠1, ∠2, ∠3是△ABC的三个外角.
求证:∠1+∠2+∠3=360°
A
B
C
1
2
3
证明:
过点A作AD∥ BC
∴ ∠2=∠4
∠3=∠DAC
(两直线平行,同位角相等)
∴ ∠1+∠2+∠3=360°
∵ ∠1+∠4+∠DAC=360°
方法三:
(周角的定义)
(等量代换)
D
4
思考 你能总结出三角形三个外角 (三个顶点处各取一个) 和的数量关系吗?
三角形的三个外角(三个顶点处各取一个) 的和等于360°.
即: 三角形的外角和等于360°.
A
B
C
D
E
1、如图,求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数.
解法一:
连接 CD
F
∵ ∠B+∠E=180°-∠BFE
∠ECD+∠BDC=180°-∠CFD
又∵ ∠BFE=∠CFD
∴ ∠B+∠E=∠ECD+∠BDC
∵∠A+∠ACE+∠ECD+∠BDC+∠ADB=180°
∴ ∠A+∠ACE+∠B+∠E+∠ADB=180°
G
巩固练习
把分散的角集中到同一个三角形中,最后利用三角形的内角和定理去解决问题.
即利用“8”字型图形的性质
总结
A
B
C
D
E
1、如图,求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数.
F
G
解法二:
∵ ∠BFC=∠B+∠E
∠CGD=∠A+∠D
又∵ ∠C+∠BFC+∠CGD=180°
∴ ∠C+∠B+∠E+∠A+∠D=180°
即 ∠A+ ∠B+ ∠C+ ∠D+ ∠E=180°
本题的两种解法都体现了化分散为集中的转化思想,
或 运用外角的性质,
巩固练习
A
B
C
D
E
F
2、如图,求 ∠A+ ∠B+ ∠C+ ∠D+ ∠E 的度数.
解法一:
连接 CB
∵ ∠E+∠F+∠EDF=180°
∠DBC+∠DCB+∠BDC=180°
又∵ ∠EDF=∠BDC
∴ ∠E+∠F=∠DBC+∠DCB
∵∠A+∠ABF+∠FBC+∠DCB+∠ACD=180°
∴ ∠A+∠ABE+∠E+∠F+∠ACB=180°
巩固练习
2、如图,求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数.
解法二:
∵ ∠BGC=∠A+∠C
∠BDG=∠DEF+∠F
又∵ ∠B+∠BGC+∠BDG=180°
∴ ∠B+∠A+∠C+∠DEF+∠F=180°
A
B
C
D
E
F
延长CD交AB于点G.
G
巩固练习
E
3、如图,试求出∠A+∠B+∠C+∠D+∠E+∠F=________.
360°
B
A
C
P
N
M
D
F
三角形的外角和等于360°.
对应练习
4、如图所示,点D,E,F分别是 △ABC 的边 BC,AC,AB 上的点,则 ∠1,∠2,∠3,∠4,∠5,∠6 这六个角的度数的和是 .
对应练习
5、如图,△ABC中,∠A=40°,
(1) 若点 P 是 ∠ABC 与 ∠ACB 平分线的交点,求 ∠P 的度数;
(2) 若点 P 是 ∠CBD 与 ∠BCE 平分线的交点,求 ∠P 的度数;
(3) 若点 P 是 ∠ABC 与 ∠ACF 平分线的交点,求 ∠P 的度数;
∠P=90°+ ∠A
1
2
∠P=90°- ∠A
1
2
∠P= ∠A
1
2
巩固练习
本节课你有什么收获?
三角形的外角
定义
由三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
性质
推论3:三角形的外角等于与它不相邻的两个内角的和
三角形的外角和
三角形的外角和等于360°
推论4:三角形的外角大于与它不相邻的任何一个内角
(三个顶点处各取一个)
