沪科版数学九年级上册第22章相似形 培优测试卷(word版 含答案)
文档属性
| 名称 | 沪科版数学九年级上册第22章相似形 培优测试卷(word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 231.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-06 11:04:51 | ||
图片预览



文档简介
沪科版九上第22章相似形培优测试卷
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 总分
得分
一、选择题
下面四组线段中,不能成比例的是()
A. B.
C. D.
如果a:b=3:2,且b是a、c的比例中项,那么b:c等于( )
A. 4:3 B. 3:4 C. 2:3 D. 3:2
如图,下列条件不能判定△ADB∽△ABC的是( )
A. ∠ABD=∠ACB
B. ∠ADB=∠ABC
C. AB2=AD AC
D. AD BC=AB2
如图,在中,,,四边形BCFE的面积为21,则的面积是( )
A.
B. 25
C. 35
D. 63
如图,DE是△ABC的中位线,点P是DE的中点,CP的延长线交AB于点Q,那么S△DPQ:S△ABC=( )
A. 1:22 B. 1:24 C. 1:26 D. 1:28
如图,Rt△ABC中,∠BAC=90°,AD⊥BC于点D,若AB=4,AC=3,则BD为( )
A. 1.8
B. 3.2
C. 2.4
D. 5
如图,在 ABCD中,F是BC边上一点,延长DF交AB的延长线于点E,若AB=3BE,则BF:CF等于( )
A. 1:2
B. 1:3
C. 2:3
D. 2:5
如图,在平行四边形ABCD中,点E在边AD上,AC,BE交于点O,若AE:ED=1:2,则S△AOE:S△COB=.( )
A. 1:2 B. 1:3 C. 1:4 D. 1:9
如图,已知△ABC与△DEF位似,位似中心为点O,且△ABC的面积与△DEF面积之比为9:4,则AO:DO的值为( )
A. 3:2 B. 3:5 C. 9:4 D. 9:5
如图,在正方形ABCD中,点E,F分别在边BC,DC上,AE、AF分别交BD于点M,N,连接CN、EN,且CN=EN.下列结论:①AN=EN,AN⊥EN;②BE+DF=EF;③∠DFE=2∠AMN;④EF2=2BM2+2DN2;⑤图中只有4对相似三角形.其中正确结论的个数是( )
A. 2 B. 3 C. 4 D. 5
二、填空题
在一张比例尺为1:100000的地图上,A、B两地间的图上距离为3厘米,则两地间的实际距离是______千米.
已知=,则的值为______.
如图,AB∥CD∥EF,若AC=2,CE=5,BD=3,则DF=______.
如图,正方形ABCD中,P为AD上一点,BP⊥PE交BC的延长线于点E,若AB=6,AP=4,则CE的长为 .
如图,在面积为24的△ABC中,矩形DEFG的边DE在AB上运动,点F、G分别在BC、AC上.若AB=8,DE=2EF,则GF的长=______.
三、解答题
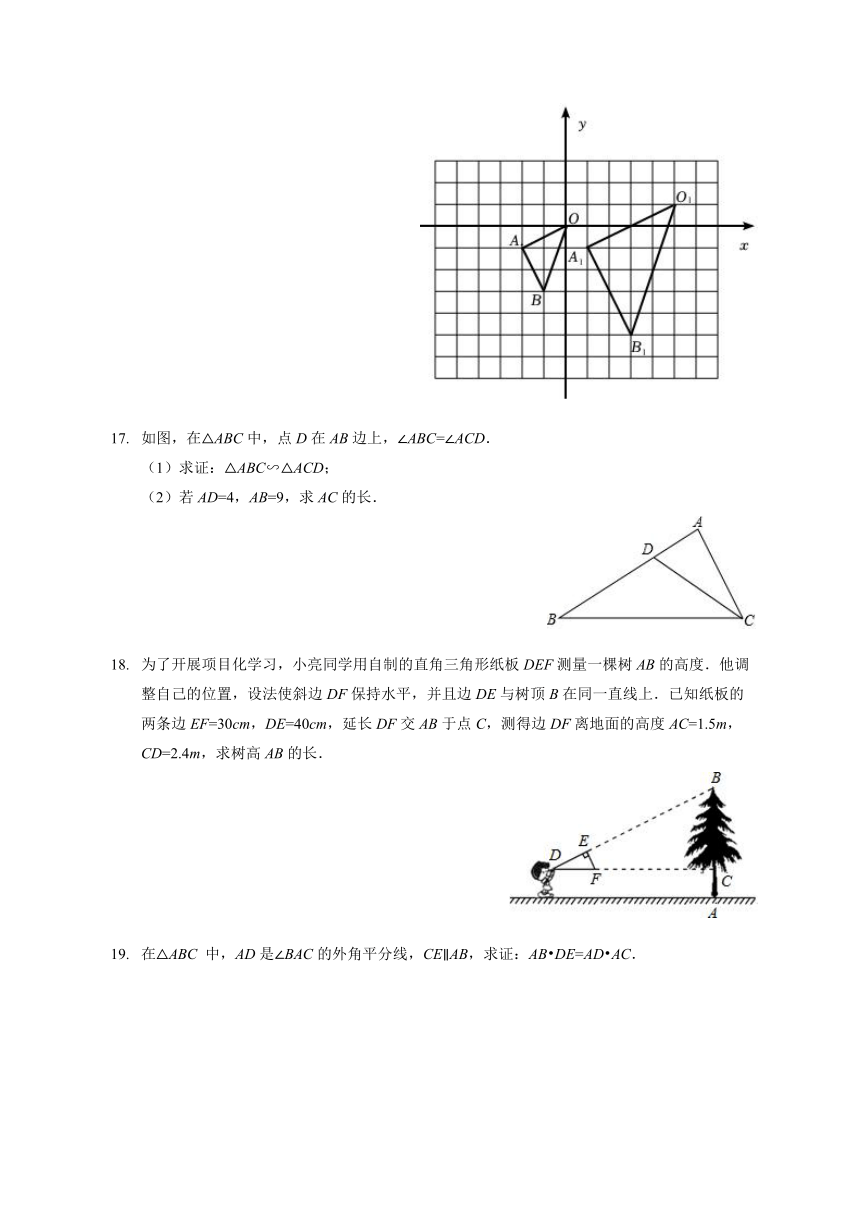
在如图的方格纸中,△OAB的顶点坐标分别为O(0,0),A(-2,-1),B(-1,-3),△O1A1B1与
△OAB是关于点P为位似中心的位似图形.
(1)在图中标出位似中心P的位置;
(2)以原点O为位似中心,在位似中心的同侧画出△OAB的一个位似△OA2B2,使它与△OAB的位似比为2:1;
(3)△OAB的内部一点M的坐标为(a,b),直接写出点M在△OA2B2中的对应点M2的坐标为______.
如图,在△ABC中,点D在AB边上,∠ABC=∠ACD.
(1)求证:△ABC∽△ACD;
(2)若AD=4,AB=9,求AC的长.
为了开展项目化学习,小亮同学用自制的直角三角形纸板DEF测量一棵树AB的高度.他调整自己的位置,设法使斜边DF保持水平,并且边DE与树顶B在同一直线上.已知纸板的两条边EF=30cm,DE=40cm,延长DF交AB于点C,测得边DF离地面的高度AC=1.5m,CD=2.4m,求树高AB的长.
在△ABC 中,AD是∠BAC的外角平分线,CE∥AB,求证:AB DE=AD AC.
如图,四边形ABGH、BCFG、CDEF是边长为1的正方形,连接BH、CH、DH,求证:∠ABH+∠ACH+∠ADH=90°.
如图①,在正方形ABCD中,AB=6,M为对角线BD上任意一点(不与B、D重合),连接CM,过点M作MN⊥CM,交线段AB于点N.
(1)求证:MN=MC;
(2)若DM:DB=2:5,求证:AN=4BN;
(3)如图②,连接NC交BD于点G.若BG:MG=3:5,求NG CG的值.
1.C 2.D 3.D 4.B 5.B 6.B 7.B 8.D 9.A 10.C
11.3
12.
13.7.5
14.7
15.4.8
16.(2a,2b)
17.(1)证明:∵∠ABC=∠ACD,∠A=∠A,
∴△ABC∽△ACD;
(2)解:∵△ABC∽△ACD,
∴=,即=,
∴AC=6.
18.解:∵∠DEF=∠DCB=90°,∠D=∠D,
∴△DEF∽△DCB,
∴,
∵EF=30cm,DE=40cm,CD=2.4m=240cm,
∴,
∴BC=180,
∵AC=1.5m=150cm,
∴AB=AC+BC=150+180=330(cm),
330cm=3.3m,
答:树高AB的长为3.3m.
19.证明:∵CE∥AB,
∴△ABD∽△ECD,
∴,
∵AD是∠BAC的外角平分线,
∴∠EAF=∠CAE,
∵CE∥AB,
∴∠EAF=∠AEC,
∴∠AEC=∠CAE,
∴AC=EC,
∴,
∴AB DE=AD AC.
20.证明:∵四边形ABGH,四边形BCFG,四边形CDEF都是正方形,
由题意BH==,BC=1,BD=2,
∴==,
又∵∠HBC=∠DBH(公共角),
∴△HBC∽△DBH,
∴∠ACH=∠DHB,
∴∠ACH+∠ADH=∠DHB+∠ADH=∠ABH=45°,
∵∠ABH=45°,
∴∠ABH+∠ACH+∠ADH=90°.
21.解:(1)如图①,过M分别作ME∥AB交BC于E,MF∥BC交AB于F,
则四边形BEMF是平行四边形,
∵四边形ABCD是正方形,
∴∠ABC=90°,∠ABD=∠CBD=∠BME=45°,
∴ME=BE,
∴平行四边形BEMF是正方形,
∴ME=MF,
∵CM⊥MN,
∴∠CMN=90°,
∵∠FME=90°,
∴∠CME=∠FMN,
∴△MFN≌△MEC(ASA),
∴MN=MC;
(2)由(1)得FM∥AD,EM∥CD,
∴===,
∴AF=2.4,CE=2.4,
∵△MFN≌△MEC,
∴FN=EC=2.4,
∴AN=4.8,BN=6-4.8=1.2,
∴AN=4BN;
(3)如图②,把△DMC绕点C逆时针旋转90°得到△BHC,连接GH,
∵△DMC≌△BHC,∠BCD=90°,
∴MC=HC,DM=BH,∠CDM=∠CBH=45°,∠DCM=∠BCH,
∴∠MBH=90°,∠MCH=90°,
∵MC=MN,MC⊥MN,
∴△MNC是等腰直角三角形,
∴∠MNC=45°,
∴∠NCH=45°,
∴△MCG≌△HCG(SAS),
∴MG=HG,
∵BG:MG=3:5,
设BG=3a,则MG=GH=5a,
在Rt△BGH中,BH=4a,则MD=4a,
∵正方形ABCD的边长为6,
∴BD=6,
∴DM+MG+BG=12a=6,
∴a=,
∴BG=,MG=,
∵∠MGC=∠NGB,∠MCG=∠ABG=45°,
∴△MGC∽△NGB,
∴=,
∴CG NG=BG MG=.
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 总分
得分
一、选择题
下面四组线段中,不能成比例的是()
A. B.
C. D.
如果a:b=3:2,且b是a、c的比例中项,那么b:c等于( )
A. 4:3 B. 3:4 C. 2:3 D. 3:2
如图,下列条件不能判定△ADB∽△ABC的是( )
A. ∠ABD=∠ACB
B. ∠ADB=∠ABC
C. AB2=AD AC
D. AD BC=AB2
如图,在中,,,四边形BCFE的面积为21,则的面积是( )
A.
B. 25
C. 35
D. 63
如图,DE是△ABC的中位线,点P是DE的中点,CP的延长线交AB于点Q,那么S△DPQ:S△ABC=( )
A. 1:22 B. 1:24 C. 1:26 D. 1:28
如图,Rt△ABC中,∠BAC=90°,AD⊥BC于点D,若AB=4,AC=3,则BD为( )
A. 1.8
B. 3.2
C. 2.4
D. 5
如图,在 ABCD中,F是BC边上一点,延长DF交AB的延长线于点E,若AB=3BE,则BF:CF等于( )
A. 1:2
B. 1:3
C. 2:3
D. 2:5
如图,在平行四边形ABCD中,点E在边AD上,AC,BE交于点O,若AE:ED=1:2,则S△AOE:S△COB=.( )
A. 1:2 B. 1:3 C. 1:4 D. 1:9
如图,已知△ABC与△DEF位似,位似中心为点O,且△ABC的面积与△DEF面积之比为9:4,则AO:DO的值为( )
A. 3:2 B. 3:5 C. 9:4 D. 9:5
如图,在正方形ABCD中,点E,F分别在边BC,DC上,AE、AF分别交BD于点M,N,连接CN、EN,且CN=EN.下列结论:①AN=EN,AN⊥EN;②BE+DF=EF;③∠DFE=2∠AMN;④EF2=2BM2+2DN2;⑤图中只有4对相似三角形.其中正确结论的个数是( )
A. 2 B. 3 C. 4 D. 5
二、填空题
在一张比例尺为1:100000的地图上,A、B两地间的图上距离为3厘米,则两地间的实际距离是______千米.
已知=,则的值为______.
如图,AB∥CD∥EF,若AC=2,CE=5,BD=3,则DF=______.
如图,正方形ABCD中,P为AD上一点,BP⊥PE交BC的延长线于点E,若AB=6,AP=4,则CE的长为 .
如图,在面积为24的△ABC中,矩形DEFG的边DE在AB上运动,点F、G分别在BC、AC上.若AB=8,DE=2EF,则GF的长=______.
三、解答题
在如图的方格纸中,△OAB的顶点坐标分别为O(0,0),A(-2,-1),B(-1,-3),△O1A1B1与
△OAB是关于点P为位似中心的位似图形.
(1)在图中标出位似中心P的位置;
(2)以原点O为位似中心,在位似中心的同侧画出△OAB的一个位似△OA2B2,使它与△OAB的位似比为2:1;
(3)△OAB的内部一点M的坐标为(a,b),直接写出点M在△OA2B2中的对应点M2的坐标为______.
如图,在△ABC中,点D在AB边上,∠ABC=∠ACD.
(1)求证:△ABC∽△ACD;
(2)若AD=4,AB=9,求AC的长.
为了开展项目化学习,小亮同学用自制的直角三角形纸板DEF测量一棵树AB的高度.他调整自己的位置,设法使斜边DF保持水平,并且边DE与树顶B在同一直线上.已知纸板的两条边EF=30cm,DE=40cm,延长DF交AB于点C,测得边DF离地面的高度AC=1.5m,CD=2.4m,求树高AB的长.
在△ABC 中,AD是∠BAC的外角平分线,CE∥AB,求证:AB DE=AD AC.
如图,四边形ABGH、BCFG、CDEF是边长为1的正方形,连接BH、CH、DH,求证:∠ABH+∠ACH+∠ADH=90°.
如图①,在正方形ABCD中,AB=6,M为对角线BD上任意一点(不与B、D重合),连接CM,过点M作MN⊥CM,交线段AB于点N.
(1)求证:MN=MC;
(2)若DM:DB=2:5,求证:AN=4BN;
(3)如图②,连接NC交BD于点G.若BG:MG=3:5,求NG CG的值.
1.C 2.D 3.D 4.B 5.B 6.B 7.B 8.D 9.A 10.C
11.3
12.
13.7.5
14.7
15.4.8
16.(2a,2b)
17.(1)证明:∵∠ABC=∠ACD,∠A=∠A,
∴△ABC∽△ACD;
(2)解:∵△ABC∽△ACD,
∴=,即=,
∴AC=6.
18.解:∵∠DEF=∠DCB=90°,∠D=∠D,
∴△DEF∽△DCB,
∴,
∵EF=30cm,DE=40cm,CD=2.4m=240cm,
∴,
∴BC=180,
∵AC=1.5m=150cm,
∴AB=AC+BC=150+180=330(cm),
330cm=3.3m,
答:树高AB的长为3.3m.
19.证明:∵CE∥AB,
∴△ABD∽△ECD,
∴,
∵AD是∠BAC的外角平分线,
∴∠EAF=∠CAE,
∵CE∥AB,
∴∠EAF=∠AEC,
∴∠AEC=∠CAE,
∴AC=EC,
∴,
∴AB DE=AD AC.
20.证明:∵四边形ABGH,四边形BCFG,四边形CDEF都是正方形,
由题意BH==,BC=1,BD=2,
∴==,
又∵∠HBC=∠DBH(公共角),
∴△HBC∽△DBH,
∴∠ACH=∠DHB,
∴∠ACH+∠ADH=∠DHB+∠ADH=∠ABH=45°,
∵∠ABH=45°,
∴∠ABH+∠ACH+∠ADH=90°.
21.解:(1)如图①,过M分别作ME∥AB交BC于E,MF∥BC交AB于F,
则四边形BEMF是平行四边形,
∵四边形ABCD是正方形,
∴∠ABC=90°,∠ABD=∠CBD=∠BME=45°,
∴ME=BE,
∴平行四边形BEMF是正方形,
∴ME=MF,
∵CM⊥MN,
∴∠CMN=90°,
∵∠FME=90°,
∴∠CME=∠FMN,
∴△MFN≌△MEC(ASA),
∴MN=MC;
(2)由(1)得FM∥AD,EM∥CD,
∴===,
∴AF=2.4,CE=2.4,
∵△MFN≌△MEC,
∴FN=EC=2.4,
∴AN=4.8,BN=6-4.8=1.2,
∴AN=4BN;
(3)如图②,把△DMC绕点C逆时针旋转90°得到△BHC,连接GH,
∵△DMC≌△BHC,∠BCD=90°,
∴MC=HC,DM=BH,∠CDM=∠CBH=45°,∠DCM=∠BCH,
∴∠MBH=90°,∠MCH=90°,
∵MC=MN,MC⊥MN,
∴△MNC是等腰直角三角形,
∴∠MNC=45°,
∴∠NCH=45°,
∴△MCG≌△HCG(SAS),
∴MG=HG,
∵BG:MG=3:5,
设BG=3a,则MG=GH=5a,
在Rt△BGH中,BH=4a,则MD=4a,
∵正方形ABCD的边长为6,
∴BD=6,
∴DM+MG+BG=12a=6,
∴a=,
∴BG=,MG=,
∵∠MGC=∠NGB,∠MCG=∠ABG=45°,
∴△MGC∽△NGB,
∴=,
∴CG NG=BG MG=.
