数学人教A版(2019)必修第一册5.4.3 正切函数的性质与图象(共23张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册5.4.3 正切函数的性质与图象(共23张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-07 21:14:34 | ||
图片预览






文档简介
(共23张PPT)
5.4.3正切函数的性质与图象
【问题】根据研究正弦函数、余弦函数的图象和性质的经验,你认为应如何研究正切函
数的图象与性质呢?
提示:研究一个新的函数,应从函数的定义域画图象,根据图象研究周期性、奇偶性、对称性、
单调性、最值(值域)等方面.
【问题】你能用不同的方法研究正切函数吗?
提示:定义域出发研究性质,再利用性质研究它的图像.
分析正切函数 是否为周期函数?哪个诱导公式能够体现?奇偶性呢?
1.周期性:由诱导公式tan(π+x)=tan x,x∈R,且x≠ +kπ,k∈Z,可知正切函数是,周期是————
周期函数
π
2.奇偶性:由诱导公式tan(-x)=-tan x,x∈R,x≠+kπ,k∈Z,可知正切函数是.
奇函数
注意点:注意区分正切函数与正弦函数、余弦函数的最小正周期,求周期的公式为:T=
0
正切函数的图像
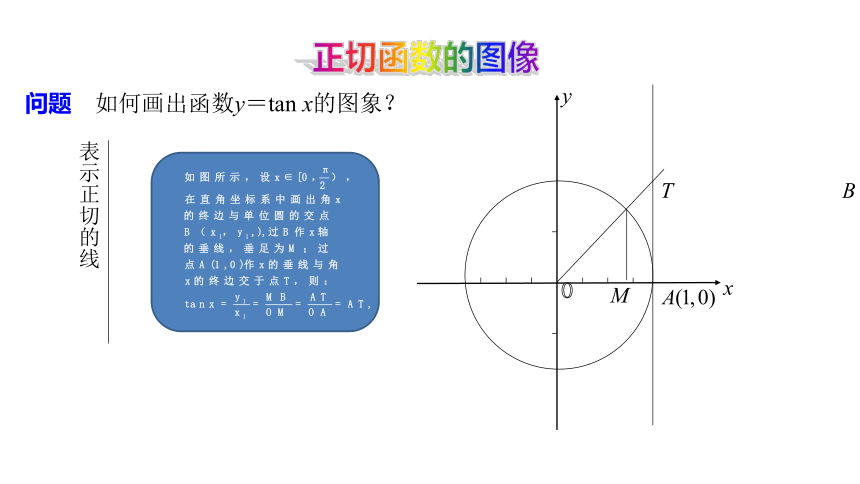
表示正切的线
问题 如何画出函数y=tan x的图象?
正切函数的图像
-1
1
0
0’
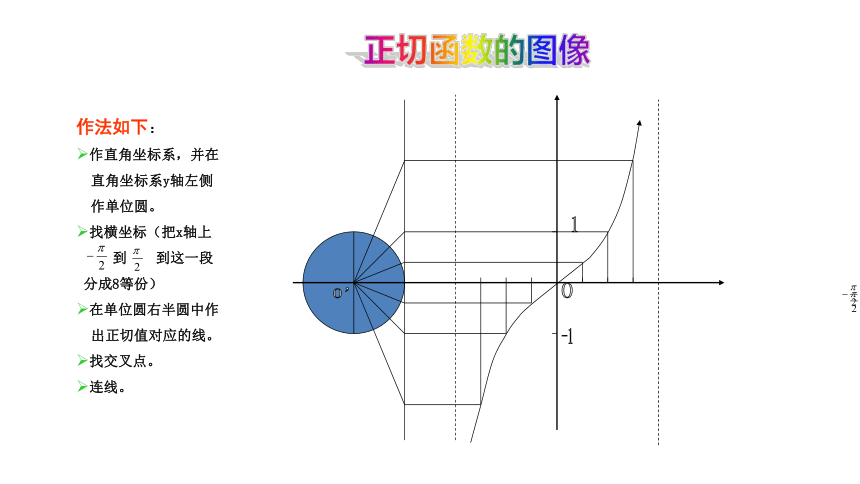
正切函数的图像
作法如下:
作直角坐标系,并在
直角坐标系y轴左侧
作单位圆。
找横坐标(把x轴上
到 到这一段
分成8等份)
在单位圆右半圆中作
出正切值对应的线。
找交叉点。
连线。
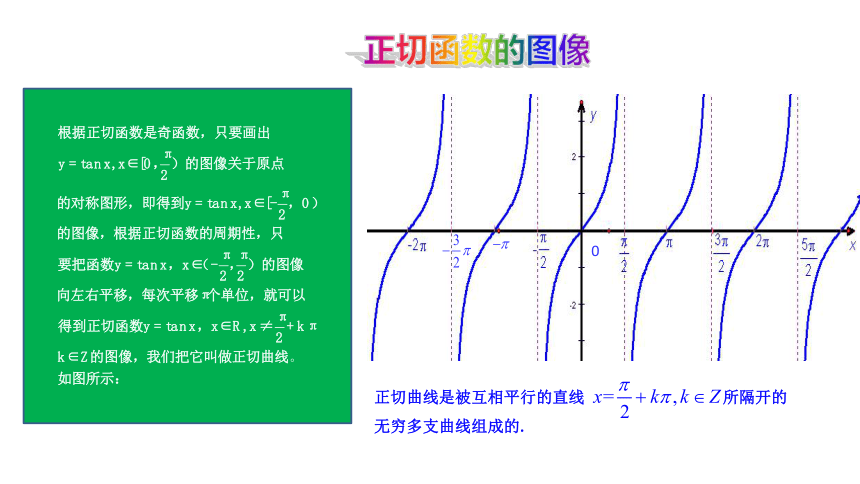
正切函数的图像
0
正切曲线是被互相平行的直线 所隔开的
无穷多支曲线组成的.
在 内为增函数
x
y
O
正切函数的性质:
(1)定义域:
(2)值域:
(3)周期性:
(4)奇偶性:
奇函数
(5)单调性:
(6)对称中心:
√
√
【悟】
(1)判断函数定义域的方法
求与正切函数有关的函数的定义域时,除了求函数定义域的一般要求外,还要保证正切函数y=tan x有意义,即x≠ +kπ,k∈Z.
(2)与正切函数有关的函数的周期性、奇偶性问题的解决策略
①一般地,函数y=Atan(ωx+φ)的最小正周期为T= ,常常利用此公式来求周期.
②判断函数的奇偶性要先求函数的定义域,判断其是否关于原点对称,若不对称,则该函数无奇偶性;若对称,再判断f(-x)与f(x)的关系.
A.奇函数 B.偶函数 C.非奇非偶函数 D.既奇又偶函数
√
解:因为f(x)=sin x+tan x,
f(-x)=sin(-x)+tan(-x)=-sin x-tan x=-f(x),故函数为奇函数.
√
【悟】正切函数对称中心的特殊性在于不仅有函数图象与x轴的交点,还有“渐近线”与x轴的交点,正确分析函数图象并结合正切函数的性质是解决与图象有关问题的关键.
【练2】(1)y=a(a为常数)与y=tan 3x图象相交时,相邻两交点间的距离为
√
√
故原函数的最小正周期为4π.
【悟】(1)运用正切函数单调性比较大小的方法
①运用函数的周期性或诱导公式将角化到同一单调区间内.
②运用单调性比较大小关系.
(2)求函数y=tan(ωx+φ)的单调区间的方法
令tan x=t,则t∈[-1,1].
故所求函数的值域为[-4,4].
∴y=-t2+4t+1=-(t-2)2+5.
【悟】解答正切函数图象与性质问题的注意点
解:
0
y
x
【练4 】(1)解下列不等式:
这个题目应该注意什么
【练4 】(2)求下列函数的单调区间:
5.4.3正切函数的性质与图象
【问题】根据研究正弦函数、余弦函数的图象和性质的经验,你认为应如何研究正切函
数的图象与性质呢?
提示:研究一个新的函数,应从函数的定义域画图象,根据图象研究周期性、奇偶性、对称性、
单调性、最值(值域)等方面.
【问题】你能用不同的方法研究正切函数吗?
提示:定义域出发研究性质,再利用性质研究它的图像.
分析正切函数 是否为周期函数?哪个诱导公式能够体现?奇偶性呢?
1.周期性:由诱导公式tan(π+x)=tan x,x∈R,且x≠ +kπ,k∈Z,可知正切函数是,周期是————
周期函数
π
2.奇偶性:由诱导公式tan(-x)=-tan x,x∈R,x≠+kπ,k∈Z,可知正切函数是.
奇函数
注意点:注意区分正切函数与正弦函数、余弦函数的最小正周期,求周期的公式为:T=
0
正切函数的图像
表示正切的线
问题 如何画出函数y=tan x的图象?
正切函数的图像
-1
1
0
0’
正切函数的图像
作法如下:
作直角坐标系,并在
直角坐标系y轴左侧
作单位圆。
找横坐标(把x轴上
到 到这一段
分成8等份)
在单位圆右半圆中作
出正切值对应的线。
找交叉点。
连线。
正切函数的图像
0
正切曲线是被互相平行的直线 所隔开的
无穷多支曲线组成的.
在 内为增函数
x
y
O
正切函数的性质:
(1)定义域:
(2)值域:
(3)周期性:
(4)奇偶性:
奇函数
(5)单调性:
(6)对称中心:
√
√
【悟】
(1)判断函数定义域的方法
求与正切函数有关的函数的定义域时,除了求函数定义域的一般要求外,还要保证正切函数y=tan x有意义,即x≠ +kπ,k∈Z.
(2)与正切函数有关的函数的周期性、奇偶性问题的解决策略
①一般地,函数y=Atan(ωx+φ)的最小正周期为T= ,常常利用此公式来求周期.
②判断函数的奇偶性要先求函数的定义域,判断其是否关于原点对称,若不对称,则该函数无奇偶性;若对称,再判断f(-x)与f(x)的关系.
A.奇函数 B.偶函数 C.非奇非偶函数 D.既奇又偶函数
√
解:因为f(x)=sin x+tan x,
f(-x)=sin(-x)+tan(-x)=-sin x-tan x=-f(x),故函数为奇函数.
√
【悟】正切函数对称中心的特殊性在于不仅有函数图象与x轴的交点,还有“渐近线”与x轴的交点,正确分析函数图象并结合正切函数的性质是解决与图象有关问题的关键.
【练2】(1)y=a(a为常数)与y=tan 3x图象相交时,相邻两交点间的距离为
√
√
故原函数的最小正周期为4π.
【悟】(1)运用正切函数单调性比较大小的方法
①运用函数的周期性或诱导公式将角化到同一单调区间内.
②运用单调性比较大小关系.
(2)求函数y=tan(ωx+φ)的单调区间的方法
令tan x=t,则t∈[-1,1].
故所求函数的值域为[-4,4].
∴y=-t2+4t+1=-(t-2)2+5.
【悟】解答正切函数图象与性质问题的注意点
解:
0
y
x
【练4 】(1)解下列不等式:
这个题目应该注意什么
【练4 】(2)求下列函数的单调区间:
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
